Summary
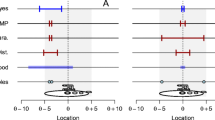
A confidence distribution function is a graphical tool for flexible statistical analyses. It provides one- and two-sided tests of simple and interval hypotheses for any size, central and symmetrical confidence intervals of any level. Given an interval of equivalent values, it quantifies the strength of evidence for “no material difference” between two populations in a set of data, but is independent of the particular choice of such an interval.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Bauer, H., 1968, “Wahrscheinlichkeitsrechnung und Grundzüge der Maβtheorie,” de Gruyter, Berlin.
Cox, D. R., 1958, Some problems connected with statistical inference, Ann. Math. Statist., 29:357.
Cox, D. R., 1977, The role of significance tests (with discussion), Scand. J. Statist., 4:49.
Kallenberg, O., 1976, “Random Measures,” Akademie-Verlag, Berlin.
Lehmann, E. L., 1959, “Testing Statistical Hypothesis,” Wiley, New York.
Mandallaz, D. and Mau, J., 1981, Comparison of different approaches to the assessment of bioequivalence, Biometrics, 37:213.
Mau, J., 1983, Die Verwendung von Fiduzialwahrscheinlichkeiten zur Beurteilung der Bioäquivalenz, in: “Biometrie in der chemisch-pharmazeutischen Industrie 1,” Vollmar, J., ed., Gustav Fischer, Stuttgart.
Mau, J., 1986, A statistical assessment of clinical equivalence, Res. Rep. 4/86, Statistics Proj. SFB 175, Univ. of Tubingen, Tubingen.
Pedersen, J. G., 1978, Fiducial inference, Internat. Statist. Rev., 46:147.
Rudin, W., 1970, “Real and Complex Analysis,” McGraw -Hill, London.
Spiegelhalter, D. J. and Freedman, L. S., 1986, A predictive approach to selecting the size of a clinical trial, based on subjective clinical opinion, Statistics in Medicine, 5:1.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 1987 Plenum Press, New York
About this chapter
Cite this chapter
Mau, J. (1987). On Cox’s Confidence Distribution. In: Viertl, R. (eds) Probability and Bayesian Statistics. Springer, Boston, MA. https://doi.org/10.1007/978-1-4613-1885-9_35
Download citation
DOI: https://doi.org/10.1007/978-1-4613-1885-9_35
Publisher Name: Springer, Boston, MA
Print ISBN: 978-1-4612-9050-6
Online ISBN: 978-1-4613-1885-9
eBook Packages: Springer Book Archive