Skip to main content
Springer Nature Link
Log in

Optimal Control

  • Chapter
  • First Online:
Process Control

  • 4292 Accesses

Abstract

Theoretically, optimal control refers to any type of control that refers to optimization methods. In reality, two main domains can be distinguished, on one side open-loop control that is also called dynamic optimization for continuous nonlinear state-space systems and dynamic programming for discrete systems. This will be explained with reference to variational calculus and includes Hamilton-Jacobi theory, Pontryagin’s maximum principle and Bellman optimality principle. On the other side, these theories are applied to closed-loop control in linear quadratic control, for perfect or stochastic systems, in continuous or discrete time. Application examples for multivariable systems illustrate linear quadratic control under different forms.

The original version of this chapter has been revised: Figs. 14.12, 14.13 and 14.14 have been corrected. The erratum to this chapter is available at https://doi.org/10.1007/978-3-319-61143-3_22.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Notes

  1. 1.

    A functional is a function of functions: the function \(F(\mathbf {x}(t),\mathbf {u}(t),t)\) depends on functions \(\mathbf {x}(t)\) and \(\mathbf {u}(t)\).

  2. 2.

    Several mathematical relations are useful:

    (a) We denote by \(y_z\) the partial derivative \(\partial y / \partial z\), where z is a scalar. If y is scalar and \(\mathbf {z}\) a vector, the notation \(y_{\mathbf {z}}\) is the gradient vector of the partial derivatives \(\partial y / \partial z_i\). If \(\mathbf {y}\) and \(\mathbf {z}\) are vectors, the notation \(\mathbf {y}_{\mathbf {z}}\) represents the Jacobian matrix of the current element \(\partial y_i / \partial z_j\).

    (b) The derivative with respect to \(\mathbf {f}\) of the integral with fixed boundaries

    $$ I = \int _{x_0}^{x_1} F(x,\mathbf {f}(x),{\dot{\mathbf {f}}}(x)) dx $$

    is equal to

    $$ \displaystyle {\frac{dI}{d\mathbf {f}}} = \int _{x_0}^{x_1} \left[ F_{\mathbf {f}} - \displaystyle {\frac{d}{dx}} F_{{\dot{\mathbf {f}}}} \right] dx $$

    (c) According to the Euler–Lagrange lemma (Cartan 1967), if \(\mathbf {C}(x)\) is a continuous function (vector) on [a, b] verifying

    $$ \int _{a}^{b} \mathbf {C}^T(x) \mathbf {v}(x) dx = 0 $$

    for all function (vector) \(\mathbf {v}(x)\) which is continuous and becomes zero at the boundaries, then \(\mathbf {C}(x)\) is zero everywhere on [a, b].

  3. 3.

    Other authors use the definition of the Hamiltonian with an opposite sign before the functional, i.e.

    $$ H(\mathbf {x}(t),\mathbf {u}(t),\mathbf {\psi }(t),t) = F(\mathbf {x}(t),\mathbf {u}(t),t) + \mathbf {\psi }^T(t) \, \mathbf {f}(\mathbf {x}(t),\mathbf {u}(t),t) $$

    which changes nothing, as long as we remain at the level of first-order conditions. However, the sign changes in condition (14.87). See also the footnote in Sect. 14.4.6.

  4. 4.

    In many articles, authors refer to the Minimum Principle, which simply results from the definition of the Hamiltonian H with an opposite sign of the functional. Comparing to definition (14.102), they define their Hamiltonian as

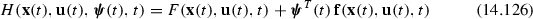
    figure a

    With that definition, the optimal control \(u^*\) minimizes the Hamiltonian.

  5. 5.

    This notation is that of Pontryaguine et al. (1974). The superscript corresponds to the rank i of the coordinate while the subscripts (0 and 1) or (0 and f), according to the authors, are reserved for the terminal conditions.

  6. 6.

    A matrix \(\mathbf {A}\) of dimension \((2n \times 2n)\) is called Hamiltonian if \(\mathbf {J}^{-1} \, \mathbf {A}^T \, \mathbf {J} = - \mathbf {A}\) or \(\mathbf {J} = - \mathbf {A}^{-T} \, \mathbf {J} \, \mathbf {A}\), where \(\mathbf {J}\) is equal to: \(\left[ \begin{array}{ll} \mathbf {0} &{} \mathbf {I} \\ \mathbf {I} &{} \mathbf {0} \end{array} \right] \).

    An important property (Laub 1979) of Hamiltonian matrices is that if \(\lambda \) is an eigenvalue of a Hamiltonian matrix, \(-\lambda \) is also an eigenvalue with the same multiplicity.

  7. 7.

    A matrix \(\mathbf {A}\) is symplectic, when, given the matrix \(J = \left[ \begin{array}{ll} \mathbf {0}&{} \mathbf {I} \\ -\mathbf {I} &{} \mathbf {0} \end{array} \right] \), the matrix \(\mathbf {A}\) verifies \(\mathbf {A}^T \, \mathbf {J} \, \mathbf {A} = \mathbf {J}\).

    If \(\lambda \) is an eigenvalue of a symplectic matrix \(\mathbf {A}\), \(1/\lambda \) is also an eigenvalue of \(\mathbf {A}\); \(\lambda \) is thus also an eigenvalue of \(\mathbf {A}^{-1}\) (Laub 1979).

References

  • B.D.O. Anderson and J.B. Moore. Linear Optimal Control. Prentice Hall, Englewood Cliffs, New Jersey, 1971.

    Google Scholar 

  • B.D.O. Anderson and J.B. Moore. Optimal Control, Linear Quadratic Methods. Prentice Hall, Englewood Cliffs, New Jersey, 1990.

    Google Scholar 

  • R. Aris. Studies in optimization. II. Optimal temperature gradients in tubular reactors. Chem. Eng. Sci., 13(1):18–29, 1960.

    Google Scholar 

  • R. Aris. The Optimal Design of Chemical Reactors: A Study in Dynamic Programming. Academic Press, New York, 1961.

    Google Scholar 

  • R. Aris, D.F. Rudd, and N.R. Amundson. On optimum cross current extraction. Chem. Eng. Sci., 12:88–97, 1960.

    Google Scholar 

  • W.F. Arnold and A.J. Laub. Generalized eigenproblem algorithms and software for algebraic Riccati equations. IEEE Proceedings, 72(12):1746–1754, 1984.

    Google Scholar 

  • M. Athans and P.L. Falb. Optimal Control: An Introduction to the Theory and its Applications. Mac Graw Hill, New York, 1966.

    Google Scholar 

  • J.R. Banga and E.F. Carrasco. Rebuttal to the comments of Rein Luus on “Dynamic optimization of batch reactors using adaptive stochastic algorithms”. Ind. Eng. Chem. res., 37:306–307, 1998.

    Google Scholar 

  • R. Bellman. Dynamic Programming. Princeton University Press, Princeton, New Jersey, 1957.

    Google Scholar 

  • R. Bellman and S. Dreyfus. Applied Dynamic Programming. Princeton University Press, Princeton, New Jersey, 1962.

    Google Scholar 

  • L.T. Biegler. Solution of dynamic optimization problems by successive quadratic programming and orthogonal collocation. Comp. Chem. Eng., 8:243–248, 1984.

    Google Scholar 

  • B. Bojkov and R. Luus. Optimal control of nonlinear systems with unspecified final times. Chem. Eng. Sci., 51(6):905–919, 1996.

    Google Scholar 

  • P. Borne, G. Dauphin-Tanguy, J.P. Richard, F. Rotella, and I. Zambettakis. Commande et Optimisation des Processus. Technip, Paris, 1990.

    Google Scholar 

  • R. Boudarel, J. Delmas, and P. Guichet. Commande Optimale des Processus. Dunod, Paris, 1969.

    Google Scholar 

  • A.E. Bryson. Dynamic Optimization. Addison Wesley, Menlo Park, California, 1999.

    Google Scholar 

  • A.E. Bryson and Y.C. Ho. Applied Optimal Control. Hemisphere, Washington, 1975.

    Google Scholar 

  • E.F. Carrasco and J.R. Banga. Dynamic optimization of batch reactors using adaptive stochastic algorithms. Ind. Eng. Chem. Res., 36:2252–2261, 1997.

    Google Scholar 

  • H. Cartan. Cours de Calcul Différentiel. Hermann, Paris, 1967.

    Google Scholar 

  • J.P. Corriou and S. Rohani. A new look at optimal control of a batch crystallizer. AIChE J., 54(12):3188–3206, 2008.

    Google Scholar 

  • J.E. Cuthrell and L.T. Biegler. On the optimization of differential-algebraic process systems. A.I.Ch.E. J., 33:1257–1270, 1987.

    Google Scholar 

  • J. Dorato and A.H. Levis. IEEE Trans. A. C., AC-16(6):613–620, 1971.

    Google Scholar 

  • J.C. Doyle. Guaranteed margins for LQG regulators. IEEE Trans. Automat. Control, AC-23:756–757, 1978.

    Google Scholar 

  • J.N. Farber and R.L. Laurence. The minimum time problem in batch radical polymerization: a comparison of two policies. Chem. Eng. Commun., 46:347–364, 1986.

    Google Scholar 

  • A. Feldbaum. Principes Théoriques des Systèmes Asservis Optimaux. Mir, Moscou, 1973. Edition Française.

    Google Scholar 

  • M. Fikar, M.A. Latifi, J.P. Corriou, and Y. Creff. Cvp-based optimal control of an industrial depropanizer column. Comp. Chem. Engn., 24:909–915, 2000.

    Google Scholar 

  • R. Fletcher. Practical Methods of Optimization. Wiley, Chichester, 1991.

    Google Scholar 

  • C. Foulard, S. Gentil, and J.P. Sandraz. Commande et Régulation par Calculateur Numérique. Eyrolles, Paris, 1987.

    Google Scholar 

  • C. Gentric, F. Pla, M.A. Latifi, and J.P. Corriou. Optimization and non-linear control of a batch emulsion polymerization reactor. Chem. Eng. J., 75:31–46, 1999.

    Google Scholar 

  • E.D. Gilles and B. Retzbach. Modeling, simulation and control of distillation columns with sharp temperature profiles. IEEE Trans. Automat. Control, AC-28(5):628–630, 1983.

    Google Scholar 

  • E.D. Gilles, B. Retzbach, and F. Silberberger. Modeling, simulation and control of an extractive distillation column. In Computer Applications to Chemical Engineering, volume 124 of ACS Symposium Series, pages 481–492, 1980.

    Google Scholar 

  • C.J. Goh and K.L. Teo. Control parametrization: a unified approach to optimal control problems with general constraints. Automatica, 24:3–18, 1988.

    Google Scholar 

  • M.J. Grimble and M.A. Johnson. Optimal Control and Stochastic Estimation: Deterministic Systems, volume 1. Wiley, Chichester, 1988a.

    Google Scholar 

  • M.J. Grimble and M.A. Johnson. Optimal Control and Stochastic Estimation: Stochastic Systems, volume 2. Wiley, Chichester, 1988b.

    Google Scholar 

  • T. Kailath. Linear Systems Theory. Prentice Hall, Englewood Cliffs, New Jersey, 1980.

    Google Scholar 

  • R.E. Kalman. A new approach to linear filtering and prediction problems. Trans. ASME Ser. D, J. Basic Eng., 82:35–45, 1960.

    Google Scholar 

  • R.E. Kalman. Mathematical description of linear dynamical systems. J. SIAM Control, series A:152–192, 1963.

    Google Scholar 

  • R.E. Kalman and R.S. Bucy. New results in linear filtering and prediction theory. Trans. ASME Ser. D, J. Basic Eng., 83:95–108, 1961.

    Google Scholar 

  • A. Kaufmann and R. Cruon. La Programmation Dynamique. Gestion Scientifique Séquentielle. Dunod, Paris, 1965.

    Google Scholar 

  • D.E. Kirk. Optimal Control Theory. An Introduction. Prentice Hall, Englewood Cliffs, New Jersey, 1970.

    Google Scholar 

  • H. Kwakernaak and R. Sivan. Linear Optimal Control Systems. Wiley-Interscience, New York, 1972.

    Google Scholar 

  • Y.D. Kwon and L.B. Evans. A coordinate transformation method for the numerical solution of non-linear minimum-time control problems. AIChE J., 21:1158–, 1975.

    Google Scholar 

  • F. Lamnabhi-Lagarrigue. Singular optimal control problems: on the order of a singular arc. Systems & control letters, 9:173–182, 1987.

    Google Scholar 

  • M.A. Latifi, J.P. Corriou, and M. Fikar. Dynamic optimization of chemical processes. Trends in Chem. Eng., 4:189–201, 1998.

    Google Scholar 

  • A.J. Laub. A Schur method for solving algebraic Riccati equations. IEEE Trans. Automat. Control, AC-24(6):913–921, 1979.

    Google Scholar 

  • E.B. Lee and L. Markus. Foundations of Optimal Control Theory. Krieger, Malabar, Florida, 1967.

    Google Scholar 

  • F.L. Lewis. Optimal Control. Wiley, New York, 1986.

    Google Scholar 

  • C.F. Lin. Advanced Control Systems Design. Prentice Hall, Englewood Cliffs, New Jersey, 1994.

    Google Scholar 

  • R. Luus. Application of dynamic programming to high-dimensional nonlinear optimal control systems. Int. J. Cont., 52(1):239–250, 1990.

    Google Scholar 

  • R. Luus. Application of iterative dynamic programming to very high-dimensional systems. Hung. J. Ind. Chem., 21:243–250, 1993.

    Google Scholar 

  • R. Luus. Optimal control of bath reactors by iterative dynamic programming. J. Proc. Cont., 4(4):218–226, 1994.

    Google Scholar 

  • R. Luus. Numerical convergence properties of iterative dynamic programming when applied to high dimensional systems. Trans. IChemE, part A, 74:55–62, 1996.

    Google Scholar 

  • R. Luus and B. Bojkov. Application of iterative dynamic programming to time-optimal control. Chem. Eng. Res. Des., 72:72–80, 1994.

    Google Scholar 

  • R. Luus and D. Hennessy. Optimization of fed-batch reactors by the Luus-Jaakola optimization procedure. Ind. Eng. Chem. Res., 38:1948–1955, 1999.

    Google Scholar 

  • J.M. Maciejowski. Multivariable Feedback Design. Addison-Wesley, Wokingham, England, 1989.

    Google Scholar 

  • W. Mekarapiruk and R. Luus. Optimal control of inequality state constrained systems. Ind. Eng. Chem. Res., 36:1686–1694, 1997.

    Google Scholar 

  • G. Pannocchia, N. Laachi, and J.B. Rawlings. A candidate to replace PID control: SISO-constrained LQ control. AIChE J., 51(4):1178–1189, 2005.

    Google Scholar 

  • L. Pontryaguine, V. Boltianski, R. Gamkrelidze, and E. Michtchenko. Théorie Mathématique des Processus Optimaux. Mir, Moscou, 1974. Edition Française.

    Google Scholar 

  • L. Pun. Introduction à la Pratique de l’Optimisation. Dunod, Paris, 1972.

    Google Scholar 

  • W.H. Ray and J. Szekely. Process Optimization with Applications in Metallurgy and Chemical Engineering. Wiley, New York, 1973.

    Google Scholar 

  • S.M. Roberts. Dynamic Programming in Chemical Engineering and Process Control. Academic Press, New York, 1964.

    Google Scholar 

  • S.M. Roberts and C.G. Laspe. Computer control of a thermal cracking reaction. Ind. Eng. Chem., 53(5):343–348, 1961.

    Google Scholar 

  • K. Schittkowski. NLPQL: A Fortran subroutine solving constrained nonlinear programming problems. Ann. Oper. Res., 5:485–500, 1985.

    Google Scholar 

  • R. Soeterboek. Predictive Control - A Unified Approach. Prentice Hall, Englewood Cliffs, New Jersey, 1992.

    Google Scholar 

  • G. Stein and M. Athans. The LQG/LTR procedure for multivariable feedback control design. IEEE Trans. Automat. Control, AC-32(2):105–114, 1987.

    Google Scholar 

  • R.F. Stengel. Optimal control and estimation. Courier Dover Publications, 1994.

    Google Scholar 

  • K.L. Teo, C.J. Goh, and K.H. Wong. A Unified Computational Approach to Optimal Control Problems. Longman Scientific & Technical, Harlow, Essex, England, 1991.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. LRGP-CNRS-ENSIC, University of Lorraine, Nancy Cedex, France

    Jean-Pierre Corriou

Authors
  1. Jean-Pierre Corriou
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jean-Pierre Corriou .

Rights and permissions

Reprints and permissions

Copyright information

© 2018 Springer International Publishing AG

About this chapter

Cite this chapter

Corriou, JP. (2018). Optimal Control. In: Process Control. Springer, Cham. https://doi.org/10.1007/978-3-319-61143-3_14

Download citation

  • DOI: https://doi.org/10.1007/978-3-319-61143-3_14

  • Published:

  • Publisher Name: Springer, Cham

  • Print ISBN: 978-3-319-61142-6

  • Online ISBN: 978-3-319-61143-3

  • eBook Packages: EngineeringEngineering (R0)

Publish with us

Policies and ethics