Skip to main content
Springer Nature Link
Log in

A General-Purpose NURBS Mesh Generation Method for Complex Geometries

  • Chapter
  • First Online:
Frontiers in Computational Fluid-Structure Interaction and Flow Simulation

  • 2072 Accesses

  • 65 Citations

Abstract

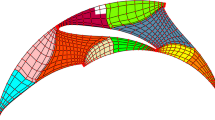
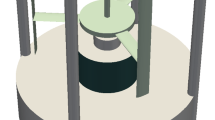
Spatial discretization with NURBS meshes is increasingly being used in computational analysis, including computational flow analysis with complex geometries. In flow analysis, compared to standard discretization methods, isogeometric discretization provides more accurate representation of the solid surfaces and increased accuracy in the flow solution. The Space-Time Computational Analysis (STCA), where the core method is the ST Variational Multiscale method, is increasingly relying on the ST Isogeometric Analysis (ST-IGA) as one of its key components, quite often also with IGA basis functions in time. The ST Slip Interface (ST-SI) and ST Topology Change methods are two other key components of the STCA, and complementary nature of all these ST methods makes the STCA powerful and practical. To make the ST-IGA use, and in a wider context the IGA use, even more practical in computational flow analysis with complex geometries, NURBS volume mesh generation needs to be easier and more automated. To that end, we present a general-purpose NURBS mesh generation method. The method is based on multi-block-structured mesh generation with existing techniques, projection of that mesh to a NURBS mesh made of patches that correspond to the blocks, and recovery of the original model surfaces to the extent they are suitable for accurate and robust fluid mechanics computations. It is expected to retain the refinement distribution and element quality of the multi-block-structured mesh that we start with. The flexibility of discretization with the general-purpose mesh generation is supplemented with the ST-SI method, which allows, without loss of accuracy, C−1 continuity between NURBS patches and thus removes the matching requirement between the patches. We present mesh-quality performance studies for 2D and 3D meshes, including those for complex models, and test computation for a turbocharger turbine and exhaust manifold. These demonstrate that the general-purpose mesh generation method proposed makes the IGA use in computational flow analysis even more practical.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

References

  1. Y. Otoguro, K. Takizawa, and T.E. Tezduyar, “Space–time VMS computational flow analysis with isogeometric discretization and a general-purpose NURBS mesh generation method”, Computers & Fluids, 158 (2017) 189–200, https://doi.org/10.1016/j.compfluid.2017.04.017.

    Article  MathSciNet  MATH  Google Scholar 

  2. T.J.R. Hughes, J.A. Cottrell, and Y. Bazilevs, “Isogeometric analysis: CAD, finite elements, NURBS, exact geometry, and mesh refinement”, Computer Methods in Applied Mechanics and Engineering, 194 (2005) 4135–4195.

    Article  MathSciNet  MATH  Google Scholar 

  3. Y. Bazilevs, V.M. Calo, Y. Zhang, and T.J.R. Hughes, “Isogeometric fluid–structure interaction analysis with applications to arterial blood flow”, Computational Mechanics, 38 (2006) 310–322.

    Article  MathSciNet  MATH  Google Scholar 

  4. Y. Bazilevs, V.M. Calo, T.J.R. Hughes, and Y. Zhang, “Isogeometric fluid–structure interaction: theory, algorithms, and computations”, Computational Mechanics, 43 (2008) 3–37.

    Article  MathSciNet  MATH  Google Scholar 

  5. Y. Bazilevs and T.J.R. Hughes, “NURBS-based isogeometric analysis for the computation of flows about rotating components”, Computational Mechanics, 43 (2008) 143–150.

    Article  MATH  Google Scholar 

  6. T.E. Tezduyar, “Stabilized finite element formulations for incompressible flow computations”, Advances in Applied Mechanics, 28 (1992) 1–44, https://doi.org/10.1016/S0065-2156(08)70153-4.

    MathSciNet  MATH  Google Scholar 

  7. T.E. Tezduyar, “Computation of moving boundaries and interfaces and stabilization parameters”, International Journal for Numerical Methods in Fluids, 43 (2003) 555–575, https://doi.org/10.1002/fld.505.

    Article  MathSciNet  MATH  Google Scholar 

  8. T.E. Tezduyar and S. Sathe, “Modeling of fluid–structure interactions with the space–time finite elements: Solution techniques”, International Journal for Numerical Methods in Fluids, 54 (2007) 855–900, https://doi.org/10.1002/fld.1430.

    Article  MathSciNet  MATH  Google Scholar 

  9. K. Takizawa and T.E. Tezduyar, “Multiscale space–time fluid–structure interaction techniques”, Computational Mechanics, 48 (2011) 247–267, https://doi.org/10.1007/s00466-011-0571-z.

    Article  MathSciNet  MATH  Google Scholar 

  10. K. Takizawa and T.E. Tezduyar, “Space–time fluid–structure interaction methods”, Mathematical Models and Methods in Applied Sciences, 22 (supp02) (2012) 1230001, https://doi.org/10.1142/S0218202512300013.

    Article  MathSciNet  MATH  Google Scholar 

  11. K. Takizawa, B. Henicke, A. Puntel, T. Spielman, and T.E. Tezduyar, “Space–time computational techniques for the aerodynamics of flapping wings”, Journal of Applied Mechanics, 79 (2012) 010903, https://doi.org/10.1115/1.4005073.

    Article  MATH  Google Scholar 

  12. K. Takizawa, B. Henicke, A. Puntel, N. Kostov, and T.E. Tezduyar, “Space–time techniques for computational aerodynamics modeling of flapping wings of an actual locust”, Computational Mechanics, 50 (2012) 743–760, https://doi.org/10.1007/s00466-012-0759-x.

    Article  MATH  Google Scholar 

  13. K. Takizawa, D. Montes, M. Fritze, S. McIntyre, J. Boben, and T.E. Tezduyar, “Methods for FSI modeling of spacecraft parachute dynamics and cover separation”, Mathematical Models and Methods in Applied Sciences, 23 (2013) 307–338, https://doi.org/10.1142/S0218202513400058.

    Article  MathSciNet  MATH  Google Scholar 

  14. K. Takizawa, T.E. Tezduyar, S. McIntyre, N. Kostov, R. Kolesar, and C. Habluetzel, “Space–time VMS computation of wind-turbine rotor and tower aerodynamics”, Computational Mechanics, 53 (2014) 1–15, https://doi.org/10.1007/s00466-013-0888-x.

    Article  MATH  Google Scholar 

  15. K. Takizawa, T.E. Tezduyar, A. Buscher, and S. Asada, “Space–time interface-tracking with topology change (ST-TC)”, Computational Mechanics, 54 (2014) 955–971, https://doi.org/10.1007/s00466-013-0935-7.

    Article  MathSciNet  MATH  Google Scholar 

  16. K. Takizawa, “Computational engineering analysis with the new-generation space–time methods”, Computational Mechanics, 54 (2014) 193–211, https://doi.org/10.1007/s00466-014-0999-z.

    Article  MathSciNet  MATH  Google Scholar 

  17. K. Takizawa, T.E. Tezduyar, A. Buscher, and S. Asada, “Space–time fluid mechanics computation of heart valve models”, Computational Mechanics, 54 (2014) 973–986, https://doi.org/10.1007/s00466-014-1046-9.

    Article  MATH  Google Scholar 

  18. K. Takizawa, T.E. Tezduyar, and A. Buscher, “Space–time computational analysis of MAV flapping-wing aerodynamics with wing clapping”, Computational Mechanics, 55 (2015) 1131–1141, https://doi.org/10.1007/s00466-014-1095-0.

    Article  Google Scholar 

  19. K. Takizawa, T.E. Tezduyar, and T. Kuraishi, “Multiscale ST methods for thermo-fluid analysis of a ground vehicle and its tires”, Mathematical Models and Methods in Applied Sciences, 25 (2015) 2227–2255, https://doi.org/10.1142/S0218202515400072.

    Article  MathSciNet  MATH  Google Scholar 

  20. K. Takizawa, T.E. Tezduyar, H. Mochizuki, H. Hattori, S. Mei, L. Pan, and K. Montel, “Space–time VMS method for flow computations with slip interfaces (ST-SI)”, Mathematical Models and Methods in Applied Sciences, 25 (2015) 2377–2406, https://doi.org/10.1142/S0218202515400126.

    Article  MathSciNet  MATH  Google Scholar 

  21. K. Takizawa, T.E. Tezduyar, T. Kuraishi, S. Tabata, and H. Takagi, “Computational thermo-fluid analysis of a disk brake”, Computational Mechanics, 57 (2016) 965–977, https://doi.org/10.1007/s00466-016-1272-4.

    Article  MathSciNet  MATH  Google Scholar 

  22. K. Takizawa, T.E. Tezduyar, Y. Otoguro, T. Terahara, T. Kuraishi, and H. Hattori, “Turbocharger flow computations with the Space–Time Isogeometric Analysis (ST-IGA)”, Computers & Fluids, 142 (2017) 15–20, https://doi.org/10.1016/j.compfluid.2016.02.021.

    Article  MathSciNet  MATH  Google Scholar 

  23. K. Takizawa, T.E. Tezduyar, S. Asada, and T. Kuraishi, “Space–time method for flow computations with slip interfaces and topology changes (ST-SI-TC)”, Computers & Fluids, 141 (2016) 124–134, https://doi.org/10.1016/j.compfluid.2016.05.006.

    Article  MathSciNet  MATH  Google Scholar 

  24. K. Takizawa, T.E. Tezduyar, T. Terahara, and T. Sasaki, “Heart valve flow computation with the integrated Space–Time VMS, Slip Interface, Topology Change and Isogeometric Discretization methods”, Computers & Fluids, 158 (2017) 176–188, https://doi.org/10.1016/j.compfluid.2016.11.012.

    Article  MathSciNet  MATH  Google Scholar 

  25. A.N. Brooks and T.J.R. Hughes, “Streamline upwind/Petrov-Galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier-Stokes equations”, Computer Methods in Applied Mechanics and Engineering, 32 (1982) 199–259.

    Article  MathSciNet  MATH  Google Scholar 

  26. T.J.R. Hughes, “Multiscale phenomena: Green’s functions, the Dirichlet-to-Neumann formulation, subgrid scale models, bubbles, and the origins of stabilized methods”, Computer Methods in Applied Mechanics and Engineering, 127 (1995) 387–401.

    Article  MathSciNet  MATH  Google Scholar 

  27. T.J.R. Hughes, A.A. Oberai, and L. Mazzei, “Large eddy simulation of turbulent channel flows by the variational multiscale method”, Physics of Fluids, 13 (2001) 1784–1799.

    Article  MATH  Google Scholar 

  28. Y. Bazilevs, V.M. Calo, J.A. Cottrell, T.J.R. Hughes, A. Reali, and G. Scovazzi, “Variational multiscale residual-based turbulence modeling for large eddy simulation of incompressible flows”, Computer Methods in Applied Mechanics and Engineering, 197 (2007) 173–201.

    Article  MathSciNet  MATH  Google Scholar 

  29. Y. Bazilevs and I. Akkerman, “Large eddy simulation of turbulent Taylor–Couette flow using isogeometric analysis and the residual–based variational multiscale method”, Journal of Computational Physics, 229 (2010) 3402–3414.

    Article  MathSciNet  MATH  Google Scholar 

  30. T.J.R. Hughes, W.K. Liu, and T.K. Zimmermann, “Lagrangian–Eulerian finite element formulation for incompressible viscous flows”, Computer Methods in Applied Mechanics and Engineering, 29 (1981) 329–349.

    Article  MathSciNet  MATH  Google Scholar 

  31. K. Takizawa, Y. Bazilevs, and T.E. Tezduyar, “Space–time and ALE-VMS techniques for patient-specific cardiovascular fluid–structure interaction modeling”, Archives of Computational Methods in Engineering, 19 (2012) 171–225, https://doi.org/10.1007/s11831-012-9071-3.

    Article  MathSciNet  MATH  Google Scholar 

  32. Y. Bazilevs, M.-C. Hsu, K. Takizawa, and T.E. Tezduyar, “ALE-VMS and ST-VMS methods for computer modeling of wind-turbine rotor aerodynamics and fluid–structure interaction”, Mathematical Models and Methods in Applied Sciences, 22 (supp02) (2012) 1230002, https://doi.org/10.1142/S0218202512300025.

    Article  MATH  Google Scholar 

  33. Y. Bazilevs, K. Takizawa, and T.E. Tezduyar, Computational Fluid–Structure Interaction: Methods and Applications. Wiley, February 2013, ISBN 978-0470978771.

    Book  MATH  Google Scholar 

  34. Y. Bazilevs, K. Takizawa, and T.E. Tezduyar, “Challenges and directions in computational fluid–structure interaction”, Mathematical Models and Methods in Applied Sciences, 23 (2013) 215–221, https://doi.org/10.1142/S0218202513400010.

    Article  MathSciNet  MATH  Google Scholar 

  35. Y. Bazilevs, K. Takizawa, and T.E. Tezduyar, “New directions and challenging computations in fluid dynamics modeling with stabilized and multiscale methods”, Mathematical Models and Methods in Applied Sciences, 25 (2015) 2217–2226, https://doi.org/10.1142/S0218202515020029.

    Article  MathSciNet  MATH  Google Scholar 

  36. V. Kalro and T.E. Tezduyar, “A parallel 3D computational method for fluid–structure interactions in parachute systems”, Computer Methods in Applied Mechanics and Engineering, 190 (2000) 321–332, https://doi.org/10.1016/S0045-7825(00)00204-8.

    Article  MATH  Google Scholar 

  37. Y. Bazilevs and T.J.R. Hughes, “Weak imposition of Dirichlet boundary conditions in fluid mechanics”, Computers and Fluids, 36 (2007) 12–26.

    Article  MathSciNet  MATH  Google Scholar 

  38. Y. Bazilevs, C. Michler, V.M. Calo, and T.J.R. Hughes, “Isogeometric variational multiscale modeling of wall-bounded turbulent flows with weakly enforced boundary conditions on unstretched meshes”, Computer Methods in Applied Mechanics and Engineering, 199 (2010) 780–790.

    Article  MathSciNet  MATH  Google Scholar 

  39. M.-C. Hsu, I. Akkerman, and Y. Bazilevs, “Wind turbine aerodynamics using ALE-VMS: Validation and role of weakly enforced boundary conditions”, Computational Mechanics, 50 (2012) 499–511.

    Article  MathSciNet  MATH  Google Scholar 

  40. M.-C. Hsu and Y. Bazilevs, “Fluid–structure interaction modeling of wind turbines: simulating the full machine”, Computational Mechanics, 50 (2012) 821–833.

    Article  MATH  Google Scholar 

  41. M.E. Moghadam, Y. Bazilevs, T.-Y. Hsia, I.E. Vignon-Clementel, A.L. Marsden, and M. of Congenital Hearts Alliance (MOCHA), “A comparison of outlet boundary treatments for prevention of backflow divergence with relevance to blood flow simulations”, Computational Mechanics, 48 (2011) 277–291, https://doi.org/10.1007/s00466-011-0599-0.

    Article  MathSciNet  MATH  Google Scholar 

  42. Y. Bazilevs, M.-C. Hsu, I. Akkerman, S. Wright, K. Takizawa, B. Henicke, T. Spielman, and T.E. Tezduyar, “3D simulation of wind turbine rotors at full scale. Part I: Geometry modeling and aerodynamics”, International Journal for Numerical Methods in Fluids, 65 (2011) 207–235, https://doi.org/10.1002/fld.2400.

    Article  MATH  Google Scholar 

  43. Y. Bazilevs, M.-C. Hsu, J. Kiendl, R. Wüchner, and K.-U. Bletzinger, “3D simulation of wind turbine rotors at full scale. Part II: Fluid–structure interaction modeling with composite blades”, International Journal for Numerical Methods in Fluids, 65 (2011) 236–253.

    Article  MATH  Google Scholar 

  44. M.-C. Hsu, I. Akkerman, and Y. Bazilevs, “High-performance computing of wind turbine aerodynamics using isogeometric analysis”, Computers and Fluids, 49 (2011) 93–100.

    Article  MathSciNet  MATH  Google Scholar 

  45. Y. Bazilevs, M.-C. Hsu, and M.A. Scott, “Isogeometric fluid–structure interaction analysis with emphasis on non-matching discretizations, and with application to wind turbines”, Computer Methods in Applied Mechanics and Engineering, 249–252 (2012) 28–41.

    Article  MathSciNet  MATH  Google Scholar 

  46. M.-C. Hsu, I. Akkerman, and Y. Bazilevs, “Finite element simulation of wind turbine aerodynamics: Validation study using NREL Phase VI experiment”, Wind Energy, 17 (2014) 461–481.

    Article  Google Scholar 

  47. A. Korobenko, M.-C. Hsu, I. Akkerman, J. Tippmann, and Y. Bazilevs, “Structural mechanics modeling and FSI simulation of wind turbines”, Mathematical Models and Methods in Applied Sciences, 23 (2013) 249–272.

    Article  MathSciNet  MATH  Google Scholar 

  48. Y. Bazilevs, K. Takizawa, T.E. Tezduyar, M.-C. Hsu, N. Kostov, and S. McIntyre, “Aerodynamic and FSI analysis of wind turbines with the ALE-VMS and ST-VMS methods”, Archives of Computational Methods in Engineering, 21 (2014) 359–398, https://doi.org/10.1007/s11831-014-9119-7.

    Article  MathSciNet  MATH  Google Scholar 

  49. Y. Bazilevs, A. Korobenko, X. Deng, and J. Yan, “Novel structural modeling and mesh moving techniques for advanced FSI simulation of wind turbines”, International Journal for Numerical Methods in Engineering, 102 (2015) 766–783, https://doi.org/10.1002/nme.4738.

    Article  MathSciNet  MATH  Google Scholar 

  50. A. Korobenko, M.-C. Hsu, I. Akkerman, and Y. Bazilevs, “Aerodynamic simulation of vertical-axis wind turbines”, Journal of Applied Mechanics, 81 (2013) 021011, https://doi.org/10.1115/1.4024415.

    Article  Google Scholar 

  51. Y. Bazilevs, A. Korobenko, X. Deng, J. Yan, M. Kinzel, and J.O. Dabiri, “FSI modeling of vertical-axis wind turbines”, Journal of Applied Mechanics, 81 (2014) 081006, https://doi.org/10.1115/1.4027466.

    Article  Google Scholar 

  52. J. Yan, A. Korobenko, X. Deng, and Y. Bazilevs, “Computational free-surface fluid–structure interaction with application to floating offshore wind turbines”, Computers and Fluids, 141 (2016) 155–174, https://doi.org/10.1016/j.compfluid.2016.03.008.

    Article  MathSciNet  MATH  Google Scholar 

  53. Y. Bazilevs, A. Korobenko, J. Yan, A. Pal, S.M.I. Gohari, and S. Sarkar, “ALE–VMS formulation for stratified turbulent incompressible flows with applications”, Mathematical Models and Methods in Applied Sciences, 25 (2015) 2349–2375, https://doi.org/10.1142/S0218202515400114.

    Article  MathSciNet  MATH  Google Scholar 

  54. Y. Bazilevs, A. Korobenko, X. Deng, and J. Yan, “FSI modeling for fatigue-damage prediction in full-scale wind-turbine blades”, Journal of Applied Mechanics, 83 (6) (2016) 061010.

    Article  Google Scholar 

  55. Y. Bazilevs, J.R. Gohean, T.J.R. Hughes, R.D. Moser, and Y. Zhang, “Patient-specific isogeometric fluid–structure interaction analysis of thoracic aortic blood flow due to implantation of the Jarvik 2000 left ventricular assist device”, Computer Methods in Applied Mechanics and Engineering, 198 (2009) 3534–3550.

    Article  MathSciNet  MATH  Google Scholar 

  56. Y. Bazilevs, M.-C. Hsu, D. Benson, S. Sankaran, and A. Marsden, “Computational fluid–structure interaction: Methods and application to a total cavopulmonary connection”, Computational Mechanics, 45 (2009) 77–89.

    Article  MathSciNet  MATH  Google Scholar 

  57. Y. Bazilevs, M.-C. Hsu, Y. Zhang, W. Wang, X. Liang, T. Kvamsdal, R. Brekken, and J. Isaksen, “A fully-coupled fluid–structure interaction simulation of cerebral aneurysms”, Computational Mechanics, 46 (2010) 3–16.

    Article  MathSciNet  MATH  Google Scholar 

  58. Y. Bazilevs, M.-C. Hsu, Y. Zhang, W. Wang, T. Kvamsdal, S. Hentschel, and J. Isaksen, “Computational fluid–structure interaction: Methods and application to cerebral aneurysms”, Biomechanics and Modeling in Mechanobiology, 9 (2010) 481–498.

    Article  Google Scholar 

  59. M.-C. Hsu and Y. Bazilevs, “Blood vessel tissue prestress modeling for vascular fluid–structure interaction simulations”, Finite Elements in Analysis and Design, 47 (2011) 593–599.

    Article  MathSciNet  Google Scholar 

  60. C.C. Long, A.L. Marsden, and Y. Bazilevs, “Fluid–structure interaction simulation of pulsatile ventricular assist devices”, Computational Mechanics, 52 (2013) 971–981, https://doi.org/10.1007/s00466-013-0858-3.

    Article  MATH  Google Scholar 

  61. C.C. Long, M. Esmaily-Moghadam, A.L. Marsden, and Y. Bazilevs, “Computation of residence time in the simulation of pulsatile ventricular assist devices”, Computational Mechanics, 54 (2014) 911–919, https://doi.org/10.1007/s00466-013-0931-y.

    Article  MathSciNet  MATH  Google Scholar 

  62. C.C. Long, A.L. Marsden, and Y. Bazilevs, “Shape optimization of pulsatile ventricular assist devices using FSI to minimize thrombotic risk”, Computational Mechanics, 54 (2014) 921–932, https://doi.org/10.1007/s00466-013-0967-z.

    Article  MathSciNet  MATH  Google Scholar 

  63. M.-C. Hsu, D. Kamensky, Y. Bazilevs, M.S. Sacks, and T.J.R. Hughes, “Fluid–structure interaction analysis of bioprosthetic heart valves: significance of arterial wall deformation”, Computational Mechanics, 54 (2014) 1055–1071, https://doi.org/10.1007/s00466-014-1059-4.

    Article  MathSciNet  MATH  Google Scholar 

  64. M.-C. Hsu, D. Kamensky, F. Xu, J. Kiendl, C. Wang, M.C.H. Wu, J. Mineroff, A. Reali, Y. Bazilevs, and M.S. Sacks, “Dynamic and fluid–structure interaction simulations of bioprosthetic heart valves using parametric design with T-splines and Fung-type material models”, Computational Mechanics, 55 (2015) 1211–1225, https://doi.org/10.1007/s00466-015-1166-x.

    Article  MATH  Google Scholar 

  65. D. Kamensky, M.-C. Hsu, D. Schillinger, J.A. Evans, A. Aggarwal, Y. Bazilevs, M.S. Sacks, and T.J.R. Hughes, “An immersogeometric variational framework for fluid-structure interaction: Application to bioprosthetic heart valves”, Computer Methods in Applied Mechanics and Engineering, 284 (2015) 1005–1053.

    Article  MathSciNet  MATH  Google Scholar 

  66. I. Akkerman, Y. Bazilevs, D.J. Benson, M.W. Farthing, and C.E. Kees, “Free-surface flow and fluid–object interaction modeling with emphasis on ship hydrodynamics”, Journal of Applied Mechanics, 79 (2012) 010905.

    Article  Google Scholar 

  67. I. Akkerman, J. Dunaway, J. Kvandal, J. Spinks, and Y. Bazilevs, “Toward free-surface modeling of planing vessels: simulation of the Fridsma hull using ALE-VMS”, Computational Mechanics, 50 (2012) 719–727.

    Article  Google Scholar 

  68. C. Wang, M.C.H. Wu, F. Xu, M.-C. Hsu, and Y. Bazilevs, “Modeling of a hydraulic arresting gear using fluid–structure interaction and isogeometric analysis”, Computers and Fluids, 142 (2017) 3–14, https://doi.org/10.1016/j.compfluid.2015.12.004.

    Article  MathSciNet  MATH  Google Scholar 

  69. M.C.H. Wu, D. Kamensky, C. Wang, A.J. Herrema, F. Xu, M.S. Pigazzini, A. Verma, A.L. Marsden, Y. Bazilevs, and M.-C. Hsu, “Optimizing fluid–structure interaction systems with immersogeometric analysis and surrogate modeling: Application to a hydraulic arresting gear”, Computer Methods in Applied Mechanics and Engineering, (2017), Published online. https://doi.org/10.1016/j.cma.2016.09.032.

    Article  MathSciNet  Google Scholar 

  70. J. Yan, X. Deng, A. Korobenko, and Y. Bazilevs, “Free-surface flow modeling and simulation of horizontal-axis tidal-stream turbines”, Computers and Fluids, 158 (2017) 157–166, https://doi.org/10.1016/j.compfluid.2016.06.016.

    Article  MathSciNet  MATH  Google Scholar 

  71. B. Augier, J. Yan, A. Korobenko, J. Czarnowski, G. Ketterman, and Y. Bazilevs, “Experimental and numerical FSI study of compliant hydrofoils”, Computational Mechanics, 55 (2015) 1079–1090, https://doi.org/10.1007/s00466-014-1090-5.

    Article  MATH  Google Scholar 

  72. J. Yan, B. Augier, A. Korobenko, J. Czarnowski, G. Ketterman, and Y. Bazilevs, “FSI modeling of a propulsion system based on compliant hydrofoils in a tandem configuration”, Computers and Fluids, 141 (2016) 201–211, https://doi.org/10.1016/j.compfluid.2015.07.013.

    Article  MathSciNet  MATH  Google Scholar 

  73. K. Takizawa and T.E. Tezduyar, “Computational methods for parachute fluid–structure interactions”, Archives of Computational Methods in Engineering, 19 (2012) 125–169, https://doi.org/10.1007/s11831-012-9070-4.

    Article  MathSciNet  MATH  Google Scholar 

  74. K. Takizawa, M. Fritze, D. Montes, T. Spielman, and T.E. Tezduyar, “Fluid–structure interaction modeling of ringsail parachutes with disreefing and modified geometric porosity”, Computational Mechanics, 50 (2012) 835–854, https://doi.org/10.1007/s00466-012-0761-3.

    Article  Google Scholar 

  75. K. Takizawa, T.E. Tezduyar, J. Boben, N. Kostov, C. Boswell, and A. Buscher, “Fluid–structure interaction modeling of clusters of spacecraft parachutes with modified geometric porosity”, Computational Mechanics, 52 (2013) 1351–1364, https://doi.org/10.1007/s00466-013-0880-5.

    Article  MATH  Google Scholar 

  76. K. Takizawa, T.E. Tezduyar, C. Boswell, R. Kolesar, and K. Montel, “FSI modeling of the reefed stages and disreefing of the Orion spacecraft parachutes”, Computational Mechanics, 54 (2014) 1203–1220, https://doi.org/10.1007/s00466-014-1052-y.

    Article  Google Scholar 

  77. K. Takizawa, T.E. Tezduyar, R. Kolesar, C. Boswell, T. Kanai, and K. Montel, “Multiscale methods for gore curvature calculations from FSI modeling of spacecraft parachutes”, Computational Mechanics, 54 (2014) 1461–1476, https://doi.org/10.1007/s00466-014-1069-2.

    Article  MathSciNet  MATH  Google Scholar 

  78. K. Takizawa, T.E. Tezduyar, C. Boswell, Y. Tsutsui, and K. Montel, “Special methods for aerodynamic-moment calculations from parachute FSI modeling”, Computational Mechanics, 55 (2015) 1059–1069, https://doi.org/10.1007/s00466-014-1074-5.

    Article  Google Scholar 

  79. K. Takizawa, T.E. Tezduyar, and R. Kolesar, “FSI modeling of the Orion spacecraft drogue parachutes”, Computational Mechanics, 55 (2015) 1167–1179, https://doi.org/10.1007/s00466-014-1108-z.

    Article  MATH  Google Scholar 

  80. K. Takizawa, B. Henicke, T.E. Tezduyar, M.-C. Hsu, and Y. Bazilevs, “Stabilized space–time computation of wind-turbine rotor aerodynamics”, Computational Mechanics, 48 (2011) 333–344, https://doi.org/10.1007/s00466-011-0589-2.

    Article  MATH  Google Scholar 

  81. K. Takizawa, B. Henicke, D. Montes, T.E. Tezduyar, M.-C. Hsu, and Y. Bazilevs, “Numerical-performance studies for the stabilized space–time computation of wind-turbine rotor aerodynamics”, Computational Mechanics, 48 (2011) 647–657, https://doi.org/10.1007/s00466-011-0614-5.

    Article  MATH  Google Scholar 

  82. K. Takizawa, Y. Bazilevs, T.E. Tezduyar, M.-C. Hsu, O. Øiseth, K.M. Mathisen, N. Kostov, and S. McIntyre, “Engineering analysis and design with ALE-VMS and space–time methods”, Archives of Computational Methods in Engineering, 21 (2014) 481–508, https://doi.org/10.1007/s11831-014-9113-0.

    Article  MathSciNet  MATH  Google Scholar 

  83. K. Takizawa, N. Kostov, A. Puntel, B. Henicke, and T.E. Tezduyar, “Space–time computational analysis of bio-inspired flapping-wing aerodynamics of a micro aerial vehicle”, Computational Mechanics, 50 (2012) 761–778, https://doi.org/10.1007/s00466-012-0758-y.

    Article  MATH  Google Scholar 

  84. K. Takizawa, B. Henicke, A. Puntel, N. Kostov, and T.E. Tezduyar, “Computer modeling techniques for flapping-wing aerodynamics of a locust”, Computers & Fluids, 85 (2013) 125–134, https://doi.org/10.1016/j.compfluid.2012.11.008.

    Article  MathSciNet  MATH  Google Scholar 

  85. K. Takizawa, T.E. Tezduyar, and N. Kostov, “Sequentially-coupled space–time FSI analysis of bio-inspired flapping-wing aerodynamics of an MAV”, Computational Mechanics, 54 (2014) 213–233, https://doi.org/10.1007/s00466-014-0980-x.

    Article  MathSciNet  MATH  Google Scholar 

  86. K. Takizawa, K. Schjodt, A. Puntel, N. Kostov, and T.E. Tezduyar, “Patient-specific computer modeling of blood flow in cerebral arteries with aneurysm and stent”, Computational Mechanics, 50 (2012) 675–686, https://doi.org/10.1007/s00466-012-0760-4.

    Article  MathSciNet  MATH  Google Scholar 

  87. K. Takizawa, K. Schjodt, A. Puntel, N. Kostov, and T.E. Tezduyar, “Patient-specific computational analysis of the influence of a stent on the unsteady flow in cerebral aneurysms”, Computational Mechanics, 51 (2013) 1061–1073, https://doi.org/10.1007/s00466-012-0790-y.

    Article  MathSciNet  MATH  Google Scholar 

  88. K. Takizawa, Y. Bazilevs, T.E. Tezduyar, C.C. Long, A.L. Marsden, and K. Schjodt, “ST and ALE-VMS methods for patient-specific cardiovascular fluid mechanics modeling”, Mathematical Models and Methods in Applied Sciences, 24 (2014) 2437–2486, https://doi.org/10.1142/S0218202514500250.

    Article  MathSciNet  MATH  Google Scholar 

  89. H. Suito, K. Takizawa, V.Q.H. Huynh, D. Sze, and T. Ueda, “FSI analysis of the blood flow and geometrical characteristics in the thoracic aorta”, Computational Mechanics, 54 (2014) 1035–1045, https://doi.org/10.1007/s00466-014-1017-1.

    Article  MATH  Google Scholar 

  90. K. Takizawa, D. Montes, S. McIntyre, and T.E. Tezduyar, “Space–time VMS methods for modeling of incompressible flows at high Reynolds numbers”, Mathematical Models and Methods in Applied Sciences, 23 (2013) 223–248, https://doi.org/10.1142/s0218202513400022.

    Article  MathSciNet  MATH  Google Scholar 

  91. K. Takizawa, T.E. Tezduyar, and H. Hattori, “Computational analysis of flow-driven string dynamics in turbomachinery”, Computers & Fluids, 142 (2017) 109–117, https://doi.org/10.1016/j.compfluid.2016.02.019.

    Article  MathSciNet  MATH  Google Scholar 

  92. K. Takizawa, T.E. Tezduyar, and T. Terahara, “Ram-air parachute structural and fluid mechanics computations with the space–time isogeometric analysis (ST-IGA)”, Computers & Fluids, 141 (2016) 191–200, https://doi.org/10.1016/j.compfluid.2016.05.027.

    Article  MathSciNet  MATH  Google Scholar 

  93. K. Takizawa, T.E. Tezduyar, and T. Kanai, “Porosity models and computational methods for compressible-flow aerodynamics of parachutes with geometric porosity”, Mathematical Models and Methods in Applied Sciences, 27 (2017) 771–806, https://doi.org/10.1142/S0218202517500166.

    Article  MathSciNet  MATH  Google Scholar 

  94. T.E. Tezduyar, S.K. Aliabadi, M. Behr, and S. Mittal, “Massively parallel finite element simulation of compressible and incompressible flows”, Computer Methods in Applied Mechanics and Engineering, 119 (1994) 157–177, https://doi.org/10.1016/0045-7825(94)00082-4.

    Article  MATH  Google Scholar 

  95. K. Takizawa and T.E. Tezduyar, “Space–time computation techniques with continuous representation in time (ST-C)”, Computational Mechanics, 53 (2014) 91–99, https://doi.org/10.1007/s00466-013-0895-y.

    Article  MathSciNet  MATH  Google Scholar 

  96. T.E. Tezduyar and D.K. Ganjoo, “Petrov-Galerkin formulations with weighting functions dependent upon spatial and temporal discretization: Applications to transient convection-diffusion problems”, Computer Methods in Applied Mechanics and Engineering, 59 (1986) 49–71, https://doi.org/10.1016/0045-7825(86)90023-X.

    Article  MATH  Google Scholar 

  97. G.J. Le Beau, S.E. Ray, S.K. Aliabadi, and T.E. Tezduyar, “SUPG finite element computation of compressible flows with the entropy and conservation variables formulations”, Computer Methods in Applied Mechanics and Engineering, 104 (1993) 397–422, https://doi.org/10.1016/0045-7825(93)90033-T.

    Article  MATH  Google Scholar 

  98. T.E. Tezduyar, “Finite elements in fluids: Stabilized formulations and moving boundaries and interfaces”, Computers & Fluids, 36 (2007) 191–206, https://doi.org/10.1016/j.compfluid.2005.02.011.

    Article  MathSciNet  MATH  Google Scholar 

  99. T.E. Tezduyar and M. Senga, “Stabilization and shock-capturing parameters in SUPG formulation of compressible flows”, Computer Methods in Applied Mechanics and Engineering, 195 (2006) 1621–1632, https://doi.org/10.1016/j.cma.2005.05.032.

    Article  MathSciNet  MATH  Google Scholar 

  100. T.E. Tezduyar and M. Senga, “SUPG finite element computation of inviscid supersonic flows with YZβ shock-capturing”, Computers & Fluids, 36 (2007) 147–159, https://doi.org/10.1016/j.compfluid.2005.07.009.

    Article  MATH  Google Scholar 

  101. T.E. Tezduyar, M. Senga, and D. Vicker, “Computation of inviscid supersonic flows around cylinders and spheres with the SUPG formulation and YZβ shock-capturing”, Computational Mechanics, 38 (2006) 469–481, https://doi.org/10.1007/s00466-005-0025-6.

    Article  MATH  Google Scholar 

  102. T.E. Tezduyar and S. Sathe, “Enhanced-discretization selective stabilization procedure (EDSSP)”, Computational Mechanics, 38 (2006) 456–468, https://doi.org/10.1007/s00466-006-0056-7.

    Article  MATH  Google Scholar 

  103. A. Corsini, F. Rispoli, A. Santoriello, and T.E. Tezduyar, “Improved discontinuity-capturing finite element techniques for reaction effects in turbulence computation”, Computational Mechanics, 38 (2006) 356–364, https://doi.org/10.1007/s00466-006-0045-x.

    Article  MathSciNet  MATH  Google Scholar 

  104. F. Rispoli, A. Corsini, and T.E. Tezduyar, “Finite element computation of turbulent flows with the discontinuity-capturing directional dissipation (DCDD)”, Computers & Fluids, 36 (2007) 121–126, https://doi.org/10.1016/j.compfluid.2005.07.004.

    Article  MATH  Google Scholar 

  105. T.E. Tezduyar, S. Ramakrishnan, and S. Sathe, “Stabilized formulations for incompressible flows with thermal coupling”, International Journal for Numerical Methods in Fluids, 57 (2008) 1189–1209, https://doi.org/10.1002/fld.1743.

    Article  MathSciNet  MATH  Google Scholar 

  106. F. Rispoli, R. Saavedra, A. Corsini, and T.E. Tezduyar, “Computation of inviscid compressible flows with the V-SGS stabilization and YZβ shock-capturing”, International Journal for Numerical Methods in Fluids, 54 (2007) 695–706, https://doi.org/10.1002/fld.1447.

    Article  MathSciNet  MATH  Google Scholar 

  107. Y. Bazilevs, V.M. Calo, T.E. Tezduyar, and T.J.R. Hughes, “YZβ discontinuity-capturing for advection-dominated processes with application to arterial drug delivery”, International Journal for Numerical Methods in Fluids, 54 (2007) 593–608, https://doi.org/10.1002/fld.1484.

    Article  MathSciNet  MATH  Google Scholar 

  108. A. Corsini, C. Menichini, F. Rispoli, A. Santoriello, and T.E. Tezduyar, “A multiscale finite element formulation with discontinuity capturing for turbulence models with dominant reactionlike terms”, Journal of Applied Mechanics, 76 (2009) 021211, https://doi.org/10.1115/1.3062967.

    Article  Google Scholar 

  109. F. Rispoli, R. Saavedra, F. Menichini, and T.E. Tezduyar, “Computation of inviscid supersonic flows around cylinders and spheres with the V-SGS stabilization and YZβ shock-capturing”, Journal of Applied Mechanics, 76 (2009) 021209, https://doi.org/10.1115/1.3057496.

    Article  Google Scholar 

  110. A. Corsini, C. Iossa, F. Rispoli, and T.E. Tezduyar, “A DRD finite element formulation for computing turbulent reacting flows in gas turbine combustors”, Computational Mechanics, 46 (2010) 159–167, https://doi.org/10.1007/s00466-009-0441-0.

    Article  MathSciNet  MATH  Google Scholar 

  111. M.-C. Hsu, Y. Bazilevs, V.M. Calo, T.E. Tezduyar, and T.J.R. Hughes, “Improving stability of stabilized and multiscale formulations in flow simulations at small time steps”, Computer Methods in Applied Mechanics and Engineering, 199 (2010) 828–840, https://doi.org/10.1016/j.cma.2009.06.019.

    Article  MathSciNet  MATH  Google Scholar 

  112. A. Corsini, F. Rispoli, and T.E. Tezduyar, “Stabilized finite element computation of NOx emission in aero-engine combustors”, International Journal for Numerical Methods in Fluids, 65 (2011) 254–270, https://doi.org/10.1002/fld.2451.

    Article  MathSciNet  MATH  Google Scholar 

  113. A. Corsini, F. Rispoli, and T.E. Tezduyar, “Computer modeling of wave-energy air turbines with the SUPG/PSPG formulation and discontinuity-capturing technique”, Journal of Applied Mechanics, 79 (2012) 010910, https://doi.org/10.1115/1.4005060.

    Article  Google Scholar 

  114. A. Corsini, F. Rispoli, A.G. Sheard, and T.E. Tezduyar, “Computational analysis of noise reduction devices in axial fans with stabilized finite element formulations”, Computational Mechanics, 50 (2012) 695–705, https://doi.org/10.1007/s00466-012-0789-4.

    Article  MathSciNet  MATH  Google Scholar 

  115. P.A. Kler, L.D. Dalcin, R.R. Paz, and T.E. Tezduyar, “SUPG and discontinuity-capturing methods for coupled fluid mechanics and electrochemical transport problems”, Computational Mechanics, 51 (2013) 171–185, https://doi.org/10.1007/s00466-012-0712-z.

    Article  MathSciNet  MATH  Google Scholar 

  116. A. Corsini, F. Rispoli, A.G. Sheard, K. Takizawa, T.E. Tezduyar, and P. Venturini, “A variational multiscale method for particle-cloud tracking in turbomachinery flows”, Computational Mechanics, 54 (2014) 1191–1202, https://doi.org/10.1007/s00466-014-1050-0.

    Article  MathSciNet  MATH  Google Scholar 

  117. F. Rispoli, G. Delibra, P. Venturini, A. Corsini, R. Saavedra, and T.E. Tezduyar, “Particle tracking and particle–shock interaction in compressible-flow computations with the V-SGS stabilization and YZβ shock-capturing”, Computational Mechanics, 55 (2015) 1201–1209, https://doi.org/10.1007/s00466-015-1160-3.

    Article  MathSciNet  MATH  Google Scholar 

  118. M.F. Wheeler, “An elliptic collocation-finite element method with interior penalties”, SIAM Journal on Numerical Analysis, 15 (1978) 152–161.

    Article  MathSciNet  MATH  Google Scholar 

  119. P. Houston, C. Schwab, and E. Suli, “Discontinuous hp-finite element methods for advection-diffusion reaction problems”, SIAM Journal on Numerical Analysis, 39 (2002) 2133–2163.

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

This work was supported (first and second authors) in part by JST-CREST; Grant-in-Aid for Challenging Exploratory Research 16K13779 from Japan Society for the Promotion of Science; Grant-in-Aid for Scientific Research (S) 26220002 from the Ministry of Education, Culture, Sports, Science and Technology of Japan (MEXT); Council for Science, Technology and Innovation (CSTI), Cross-Ministerial Strategic Innovation Promotion Program (SIP), “Innovative Combustion Technology” (Funding agency: JST); and Rice–Waseda research agreement. This work was also supported (third author) in part by ARO Grant W911NF-17-1-0046 and Top Global University Project of Waseda University.

Author information

Authors and Affiliations

  1. Department of Modern Mechanical Engineering, Waseda University, Shinjuku-ku, Tokyo, Japan

    Yuto Otoguro & Kenji Takizawa

  2. Mechanical Engineering, Rice University, Houston, TX, USA

    Tayfun E. Tezduyar

  3. Faculty of Science and Engineering, Waseda University, Shinjuku-ku, Tokyo, Japan

    Tayfun E. Tezduyar

Authors
  1. Yuto Otoguro
    View author publications

    Search author on:PubMed Google Scholar

  2. Kenji Takizawa
    View author publications

    Search author on:PubMed Google Scholar

  3. Tayfun E. Tezduyar
    View author publications

    Search author on:PubMed Google Scholar

Corresponding author

Correspondence to Yuto Otoguro .

Editor information

Editors and Affiliations

  1. Mechanical Engineering, Rice University, Houston, TX, USA

    Tayfun E. Tezduyar

Rights and permissions

Reprints and permissions

Copyright information

© 2018 Springer Nature Switzerland AG

About this chapter

Check for updates. Verify currency and authenticity via CrossMark

Cite this chapter

Otoguro, Y., Takizawa, K., Tezduyar, T.E. (2018). A General-Purpose NURBS Mesh Generation Method for Complex Geometries. In: Tezduyar, T. (eds) Frontiers in Computational Fluid-Structure Interaction and Flow Simulation. Modeling and Simulation in Science, Engineering and Technology. Birkhäuser, Cham. https://doi.org/10.1007/978-3-319-96469-0_10

Download citation

Publish with us

Policies and ethics