Abstract
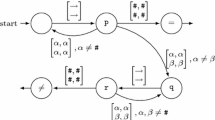
A reversible Turing machines is a computing model with a “backward deterministic” property, which is closely related to physical reversibility. In this paper, we study the problem of finding a small universal reversible Turing machine (URTM). As a result, we obtained a 17-state 5-symbol URTM in the quintuple form that can simulate any cyclic tag system.
This is a preview of subscription content, log in via an institution to check access.
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Baiocchi, C.: Three small universal Turing machines. In: Margenstern, M., Rogozhin, Y. (eds.) MCU 2001. LNCS, vol. 2055, pp. 1–10. Springer, Heidelberg (2001)
Bennett, C.H.: Logical reversibility of computation. IBM J. Res. Dev. 17, 525–532 (1973)
Cook, M.: Universality in elementary cellular automata. Complex Systems 15, 1–40 (2004)
Woods, D., Neary, T.: On the time complexity of 2-tag systems and small universal Turing machines. In: Proc. of 47th Symposium on Foundations of Computer Science (FOCS), pp. 439–446 (2006)
Fredkin, E., Toffoli, T.: Conservative logic. Int. J. Theoret. Phys. 21, 219–253 (1982)
Kudlek, M., Rogozhin, Y.: A universal Turing machine with 3 states and 9 symbols. In: Kuich, W., Rozenberg, G., Salomaa, A. (eds.) DLT 2001. LNCS, vol. 2295, pp. 311–318. Springer, Heidelberg (2002)
Minsky, M.L.: Computation: Finite and Infinite Machines. Prentice-Hall, Englewood Cliffs (1967)
Morita, K., Shirasaki, A., Gono, Y.: A 1-tape 2-symbol reversible Turing machine. Trans. IEICE Japan E-72, 223–228 (1989)
Morita, K., Harao, M.: Computation universality of one-dimensional reversible (injective) cellular automata. Trans. IEICE Japan E-72, 758–762 (1989)
Morita, K.: A simple universal logic element and cellular automata for reversible computing. In: Margenstern, M., Rogozhin, Y. (eds.) MCU 2001. LNCS, vol. 2055, pp. 102–113. Springer, Heidelberg (2001)
Morita, K., Ogiro, T.: Simple universal reversible cellular automata in which reversible logic elements can be embedded. IEICE Trans. on Information and Systems E87-D, 650–656 (2004)
Morita, K.: Simple universal one-dimensional reversible cellular automata. Journal of Cellular Automata (in press)
Rogozhin, Y.: Small universal Turing machines. Theoretical Computer Science 168, 215–240 (1996)
Rogozhin, Y.: A universal Turing machine with 22 states and 2 symbols. Romanian J. Inform. Sci. Technol. 1, 259–265 (1998)
Toffoli, T.: Reversible computing. In: de Bakker, J.W., van Leeuwen, J. (eds.) Automata, Languages and Programming. LNCS, vol. 85, pp. 632–644. Springer, Heidelberg (1980)
Toffoli, T.: Bicontinuous extensions of invertible combinatorial functions. Mathematical Systems Theory 14, 12–23 (1981)
Author information
Authors and Affiliations
Editor information
Rights and permissions
Copyright information
© 2007 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Morita, K., Yamaguchi, Y. (2007). A Universal Reversible Turing Machine. In: Durand-Lose, J., Margenstern, M. (eds) Machines, Computations, and Universality. MCU 2007. Lecture Notes in Computer Science, vol 4664. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-74593-8_8
Download citation
DOI: https://doi.org/10.1007/978-3-540-74593-8_8
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-540-74592-1
Online ISBN: 978-3-540-74593-8
eBook Packages: Computer ScienceComputer Science (R0)