Hypersonic Flow

Abstract

General overview of hypersonic flow theory is given starting with Newtonian impact theory based on the momentum transfer of air particles normal to a wall. Afterwards, modified Newtonian theory based on the stagnation pressure correction to the original theory is introduced. In completing the Newtonian flow centripetal force correction is applied to the hypersonic flow past curved walls. In addition, unsteady Newtonian flow is introduced to examine the oscillatory hypersonic flows past blunt bodies. The piston theory based on the Hayes’ hypersonic similarity rule is developed and applied to slender wings. There exist first, second or third order piston theories depending on the value of the hypersonic similarity parameter (Mτ). The modified piston theory on the other hand, handles the unsteady hypersonic flows past wings with sharp leading edges but considerable thickness effects especially because of thick boundary layers. Maslen’s simple numerical method is given for the inverse solution of the hypersonic flows past simple shapes. In addition numerical solutions of Euler’s equation for a space capsule and shuttle like configurations at various high Mach numbers are provided. Viscous flow analysis and aerodynamic heating and viscous interaction concepts are given in terms of heat transfer at the walls in hypersonic flows. In addition, strong heat transfer effects causing structural damages because of the shock boundary layer interaction is briefly mentioned. The high temperature effects on the specific heat constants of air is studied with the introduction of the vibrational effects of the diatomic molecules like oxygen and nitrogen. The concept of aerothermodynamics is briefly introduced. The composition of air with respect to altitude and speed is provided to assess the disassociation of molecules and the chemical reactions among the oxygen and nitrogen atoms. The equilibrium and non-equilibrium reacting flow concepts are utilized to see the effect of air composition on the temperature field and on the shock position involving blunt body flows. The chemical kinetics for a 1-D flow is provided to describe the flow with chemical non-equilibrium. In addition, a comparison for 2-D curved shock in front of a sphere obtained with chemical kinetics, chemical equilibrium, frozen flow and the perfect gas flow is provided. With this the concept of aerothermochemistry is briefly mentioned. The computational solution to viscous hypersonic flow studies are given for the stagnation flow and the multidimensional reacting flows to find the skin friction and the heat transfer rates based on the Reynolds and the Stanton numbers. The concept of catalycity of walls are introduced in terms of binary diffusion. The nondimensional Lewis number is introduced to show this effect on the energy equation. Finally, the waverider concept is given to yield maximum L/D ratio for hypersonic flying vehicles. The inviscid and the viscous aspects of the waverider are also provided with simple cone flow analysis as well as the modern computational techniques involving solutions of Euler and Navier–Stokes equations. The possible realization of manned or unmanned hypersonic flight based on the waverider concept in near future is stressed.

Problems and Questions

7.1:

For a given free stream Mach number M, obtain the stagnation pressure coefficient in terms of M. Find the limit of the stagnation pressure coefficient for M approaching infinity

7.2:

Use the point at the surface and the first point Δn away from the surface, obtain Eq. 7.11 from Eq. 7.10 which gives the pressure caused by the curvature (take R = −1/(dθ/ds))

7.3:

Using Newton–Busemann theory obtain the surface pressure distribution of a circular cylinder at free stream speed of M = 8, and compare the results with Newton and improved Newton method

7.4:

Find the surface pressure distribution of a 2-D body whose surface equation is given with z _u  = x ^1/2, 0 ≤ x ≤ 1, and pitching about its leading edge at angle of attack amplitude of 5° and k = 0.5

7.5:

A body of revolution is given with equation of radius r: x = 0.79r ² − 1, −1 ≤ x ≤ 0, with respect to symmetry axis x. Obtain the surface pressure distribution with Newtonian and improved Newtonian theory

7.6:

Find the surface pressure distribution of the body of Problem 7.5 which oscillates about its nose with angle of attack amplitude of 5° and k = 0.4

7.7:

Obtain the surface pressure distribution of a spherical segment which has an apex angle of 60° and 2 m radius oscillating about its nose with small amplitude

7.8:

Obtain Eq. 7.6 for steady flows using Eq. 7.20 which expresses surface pressure distribution

7.9:

Newtonian impact theory is non linear. Why?

7.10:

Find the sectional drag coefficient for a circular cylinder in hypersonic flow using Newton–Busemann theory

7.11:

Obtain Eq. 7.24 from Eq. 7.21 with expanding the equation into the series in terms of powers of w/a

7.12:

For a 5% thick airfoil find the free stream Mach number for which: (1) first order, (2) second order and (3) third order piston theory is applicable

7.13:

What should be the minimum value of reduced frequency k for a thin airfoil in a free stream Mach number of 6 so that the piston theory is valid?

7.14:

Why is it necessary to consider the thickness effect for a thin airfoil in hypersonic aerodynamics?

7.15:

Find the surface pressure distribution of a 5% thick parabolic airfoil in a free stream Mach number of 5 at altitude of 50 km

7.16:

The profile given in Problem 7.12. is in plunging motion with k = 0.3. Determine the upper surface pressure distribution in terms of the amplitude of plunging

7.17:

Using the improved piston theory for the profile given in Problem 7.13 find the lifting pressure distribution. What can be the thickness ratio for the same profile at free stream of M = 3?

7.18.:

Find the lifting pressure distribution for the profile given in Problem 7. 16 at free stream Mach number of M = 3

7.19:

Equation 7.36a, is written for the conservation of momentum in y direction. Obtain Eq. 7.36b wherein the stream function is independent variable

7.20:

Obtain the oblique shock relations in terms of Mach number M, shock angle θ _s , the specific heat ratios γ

7.21:

Show that the enthalpy can be expressed in terms of the pressure and the density as follows: h = 2γ/(γ − 1)(p/ρ)

7.22:

Find the pressure, density, enthalpy and the surface velocity of Example 7.2 for the streamline value of χ = 0.0625

7.23:

Use the Maslen method to find the flow conditions at a point with seen with 30° angle from the center of a circular cylinder in free stream Mach number of infinity

7.24:

Show that the Maslen method gives: tan θ _s  = [11 − (121 − 48 tan² θ _c )^1/2]/2tan θ _c for the the shock angle θ _s of a cone with cone angle θ _c in a free stream Mach number of infinity with γ = 1.4

7.25:

What is the advantage of the Maslen method over the Newtonian impact theory?

7.26:

Using the Maslen method find the change in the shock angle at the nose of a cone pitching with about its nose with a small amplitude (Use body attached coordinate system as done in Example 7.1)

7.27:

Obtain the Jacobian fluxes A _i  = ∂F _i / ∂U in Equation 7.47 for i = 1, 2

7.28:

The coefficient λ = 1/2 h ²|∂u _l /∂x _l | is used to prevent the numerical oscillations at a shock. Obtain the expression for |∂u _l /∂x _l | in terms of the velocity components if x _l is the direction showing the magnitude of the gradient of a velocity vector in an element

7.29:

An empirical way to determine shock shapes based on experiments is given by Billig (1967). A shape of shock created by a blunt body in x–y coordinate system is given as a hyperbola x = R + δ − R _c  cot² β[(1 + y ² tan² β/R ² _c )^1/2 − 1]. Here, the blunt body is taken as sphere-cone junction with δ: the shock distance, R: the radius of the sphere and R _c : the shock curvature to give

$$ {\text{d}}/R = 0. 1 4 3 {\text{ exp(3}}. 2 4/M^{ 2} ),\quad R_{{c}} /R = 1. 1 4 3 {\text{ exp[}}0. 5 4/({\text{M}}^{ 2} - 1)^{ 1. 2} ]. $$

Here, β is the attached shock angle of the cone alone. Plot the shape of the shock generated by the solid surface shown above for Mach numbers of M = 4 and 8

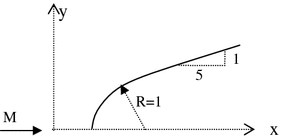
7.30:

Using Maslen method, find the approximate value of pressure and density at the junction of the sphere and the cone of Problem 7.29 at Mach number 8

7.31:

A flat plate of 4 m long has the wall temperature of 1,200 K at zero angle of attack at free stream Mach number of 25 and 85 km altitude. Using the data given obtain the pressure variation along the plate

7.32:

Find the induced pressure on the surface of cone given in Example 7.3 with the free stream conditions described at Problem 7.31

7.33:

Find the heat transfer rate q _w at x = 10 and 100 cm for the flat plate given in Problem 7.31

7.34:

Show that the derivative of the boundary layer edge velocity is given by Eq. 7.64 for the figure given below

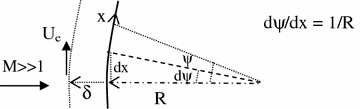
7.35:

Obtain aerodynamic heating formula for at the stagnation point of a sphere in term s of radius of curvature. Assuming calorically perfect air, find the aerodynamic heating of the space capsule given in Fig. 7.9. Take the wall temperature as 1,200 K. Find also the heating rate at ψ = 45°

7.36:

Show that Eq. 7.68 gives the rate of heating in terms of the surface pressure change for the shock boundary layer interaction

7.37:

For a diatomic molecule find the contribution of the vibration energy to the specific heat under constant volume. Neglect the ground level energy effect to the partition function

7.38:

Find the specific internal energy and the enthalpy of the air under 1 atmosphere pressure and 2,000 K

7.39:

The surface area of the space shuttle is designed to be 560,000 in². Determine the lift coefficient of the shuttle during its re-entry

7. 40:

Solve Example 7.5 with equilibrium energy as the initial condition for the Oxygen molecule at 1 atmosphere and 3,200 K

7.41:

For N₂ + O₂ → 2 N + O₂ plot the graph of forward reaction in 6,000–9,000 K interval and compare with the production of 2O from O₂

7.42:

In pure N₂ flow, find the temperature and density change with respect x coordinate behind the normal shock created with M = 12.28, T = 300 K and p = 1/760 atm

7.43:

Using the energy equation obtain Eq. 7.95 for the stagnation enthalpy h _o in terms of local Prandtl and Lewis numbers

7.44:

Find for a waverider flying at 80 km altitude with a Mach number of 25, find: (1) approximate lifting pressure, (2) lift coefficient, and induced drag coefficient. Assume ideal flow

7.45:

If the waverider of the Problem 7.44 has the wall temperature of 1,400 K and Re = 1.371 × 10⁶ with respect to its length then find the drag coefficient with reference temperature method. Use this result to determine (L/D) with total drag