Satellite Dynamics About Asteroids: Computing Poincaré Maps for the General Case

Abstract

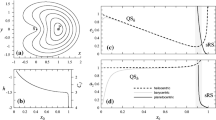
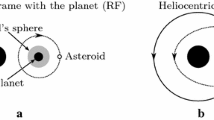
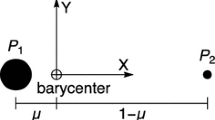
The study of orbital dynamics of spacecraft about non-spherical bodies has usually been restricted to the “planetary” case where the body is close to an oblate spheroid, with only a relatively small degree of equatorial ellipticity. When investigating spacecraft dynamics about asteroids, the situation is drastically different as the asteroid shape is usually very distended with many irregular features. Research into the dynamics of particles about asteroids accounting for their generalized shape has only been initiated relatively recently ([1], [4], [5]). This communication outlines an algorithm to compute Poincaré maps and their associated monodromy matrices about arbitrary shapes. This capability is vital for systematic investigations of motion in this problem.