Abstract
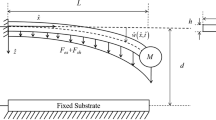
In two past decades, there are so many works representing to elastic behaviors of cantilever MEMS actuators in the micro and nanoscales for various loading conditions and geometries. However, there are little efforts available for the permanent plastic behavior of the MEMS structures and actuators. In addition, the most size—dependent plasticity considerations based on gradient models have been limited to primary concepts on material modeling or microstructural evolution as compared with structural analyses. In this paper, a conventional mechanism-based strain gradient (CMSG) plasticity theory is applied to investigate permanent behavior of the cantilever micro-beam actuators, by determining the effect of length scale on flexural displacement. If the beam is scaled to micron size, mechanical behavior follows from material dimension or length scale. While the model consisted of a multiple plastic work hardening, its kinematics is established on the Euler–Bernoulli hypothesis. The deflection of cantilever MEMS actuator is determined for different cases of the loading and length scales, compared with other relevant theoretical and experimental observations. Also, the effect of the elastic medium of the environmental foundation is considered for the actuator, dedicatedly.








Similar content being viewed by others
Explore related subjects
Discover the latest articles and news from researchers in related subjects, suggested using machine learning.References
Acharya A, Beaudoin AJ (2000) Grain-size effect in viscoplastic polycrystals at moderate strains. J Mech Phys Solids 48:2213–2230. https://doi.org/10.1016/S0022-5096(00)00013-2
Aifantis EC (1984) On the microstructural origin of certain inelastic models. J Eng Mater Technol 106:326. https://doi.org/10.1115/1.3225725
Aifantis EC (1987) The physics of plastic deformation. Int J Plast 3:211–247. https://doi.org/10.1016/0749-6419(87)90021-0
Arsenlis A, Parks DM (1999) Crystallographic aspects of geometrically-necessary and statistically-stored dislocation density. Acta Mater 47:1597–1611. https://doi.org/10.1016/S1359-6454(99)00020-8
Azizi R, Niordson CF, Legarth BN (2014) On the homogenization of metal matrix composites using strain gradient plasticity. Acta Mech Sin 30:175–190. https://doi.org/10.1007/s10409-014-0028-7
Ban H, Yao Y, Chen S, Fang D (2017) The coupling effect of size and damage in micro-scale metallic materials. Int J Plast 95:251–263. https://doi.org/10.1016/j.ijplas.2017.04.012
Ban H, Yao Y, Chen S, Fang D (2019) A new constitutive model of micro-particle reinforced metal matrix composites with damage effects. Int J Mech Sci 1:2. https://doi.org/10.1016/j.ijmecsci.2019.01.024
Bassani JL (2001) Incompatibility and a simple gradient theory of plasticity. J Mech Phys Solids 49:1983–1996
Bishop JFW, Hill R (1951a) CXXVIII. A theoretical derivation of the plastic properties of a polycrystalline face-centred metal. Lond Edinb Dublin Philos Mag J Sci 42:1298–1307. https://doi.org/10.1080/14786444108561385
Bishop JFW, Hill R (1951b) A theory of the plastic distortion of a polycrystalline aggregate under combined stresses. Philos Mag Ser 7(42):414–427. https://doi.org/10.1080/14786445108561065
Cermelli P, Gurtin ME (2002) Geometrically necessary dislocations in viscoplastic single crystals and bicrystals undergoing small deformations. Int J Solids Struct 39:6281–6309. https://doi.org/10.1016/S0020-7683(02)00491-2
Challamel N, Wang CM (2008) The small length scale effect for a non-local cantilever beam: a paradox solved. Nanotechnology 19:1–7. https://doi.org/10.1088/0957-4484/19/34/345703
Chen SH, Feng B (2011) Size effect in micro-scale cantilever beam bending. Acta Mech 219:291–307. https://doi.org/10.1007/s00707-011-0461-7
Chen SH, Wang TC (2000) New hardening law for strain gradient plasticity. Acta Mater 48:3997–4005. https://doi.org/10.1016/S1359-6454(00)00216-0
Chen SH, Wang TC (2002a) Finite element solutions for plane strain mode I crack with strain gradient effects. Int J Solids Struct 39:1241–1257. https://doi.org/10.1016/S0020-7683(01)00233-5
Chen SH, Wang TC (2002b) Size effects in the particle-reinforced metal-matrix composites. Acta Mech 157:113–127. https://doi.org/10.1007/BF01182158
Chen SH, Wang TC (2002c) A new deformation theory with strain gradient effects. Int J Plast 18:971–995. https://doi.org/10.1016/S0749-6419(01)00020-1
Chen SH, Tao CJ, Wang TC (2004) A study of size-dependent microindentation. Acta Mech 167:57–71. https://doi.org/10.1007/s00707-003-0064-z
Chen S, Liu L, Wang T (2005) Investigation of the mechanical properties of thin films by nanoindentation, considering the effects of thickness and different coating-substrate combinations. Surf Coatings Technol 191:25–32. https://doi.org/10.1016/j.surfcoat.2004.03.037
Chen SH, Liu L, Wang TC (2007) Small scale, grain size and substrate effects in nano-indentation experiment of film-substrate systems. Int J Solids Struct 44:4492–4504. https://doi.org/10.1016/j.ijsolstr.2006.11.033
Chen S, Feng B, Wei Y, Wang T (2011) Prediction of the initial thickness of shear band localization based on a reduced strain gradient theory. Int J Solids Struct 48:3099–3111. https://doi.org/10.1016/j.ijsolstr.2011.07.007
Demiral M, Roy A, Silberschmidt VV (2016) Strain-gradient crystal-plasticity modelling of micro-cutting of b.c.c. single crystal. Meccanica 51:371–381. https://doi.org/10.1007/s11012-015-0280-3
Elmustafa AA, Stone DS (2002) Indentation size effect in polycrystalline. F C C Metals 50:3641–3650
Ertürk I, van Dommelen JAW, Geers MGD (2014) Gradient crystal plasticity modelling of anelastic effects in particle strengthened metallic thin films. Meccanica 49:2657–2685. https://doi.org/10.1007/s11012-014-9907-z
Evers L, Brekelmans WA, Geers MG (2004) Scale dependent crystal plasticity framework with dislocation density and grain boundary effects. Int J Solids Struct 41:5209–5230. https://doi.org/10.1016/j.ijsolstr.2004.04.021
Fleck NA, Hutchinson JW (1993) A phenomenological theory for strain gradient effects in plasticity. J Mech Phys Solids 41:1825–1857. https://doi.org/10.1016/0022-5096(93)90072-N
Fleck NA, Hutchinson Jv (1997) Strain gradient plasticity. Adv Appl Mech 33:295–361
Fleck NA, Hutchinson JW (2001) A reformulation of strain gradient plasticity. J Mech Phys Solids 49:2245–2271. https://doi.org/10.1016/S0022-5096(01)00049-7
Fleck NA, Willis JR (2009) A mathematical basis for strain-gradient plasticity theory. Part II: tensorial plastic multiplier. J Mech Phys Solids 57:1045–1057. https://doi.org/10.1016/j.jmps.2009.03.007
Fleck NA, Willis JR (2015) Strain gradient plasticity: energetic or dissipative? Acta Mech Sin Xuebao 31:465–472. https://doi.org/10.1007/s10409-015-0468-8
Fleck Na, Muller GM, Ashby MF, Hutchinson JW (1994) Strain gradient plasticity: theory and experiment. Acta Metall Mater 42:475–487. https://doi.org/10.1016/0956-7151(94)90502-9
Gao H, Huang Y, Nix WD (1999a) Modeling plasticity at the micrometer scale. Naturwissenschaften 86:507–515. https://doi.org/10.1007/s001140050665
Gao H, Huang Y, Nix WD, Hutchinson JW (1999b) Mechanism-based strain gradient plasticity—I. Theory. J Mech Phys Solids 47:1239–1263. https://doi.org/10.1016/S0022-5096(98)00103-3
Geers MGD, Brekelmans WAM, Bayley CJ (2007) Second-order crystal plasticity: Internal stress effects and cyclic loading. Model Simul Mater Sci Eng. https://doi.org/10.1088/0965-0393/15/1/s12
Gudmundson P (2004) A unified treatment of strain gradient plasticity. J Mech Phys Solids 52:1379–1406. https://doi.org/10.1016/j.jmps.2003.11.002
Gurtin ME (2000) On the plasticity of single crystals : free energy, microforces, plastic-strain gradients. J Mech Phys Solids 48:989–1036
Gurtin ME, Anand L (2005) A theory of strain-gradient plasticity for isotropic, plastically irrotational materials. Part II: finite deformations. Int J Plast 21:2297–2318. https://doi.org/10.1016/j.ijplas.2005.01.006
Huang Y, Gao H, Nix WD, Hutchinson JW (2000) Mechanism-based strain gradient plasticity—II. Analysis. J Mech Phys Solids 48:99–128. https://doi.org/10.1016/S0022-5096(99)00022-8
Huang Y, Qu S, Hwang KC et al (2004) A conventional theory of mechanism-based strain gradient plasticity. Int J Plast 20:753–782. https://doi.org/10.1016/j.ijplas.2003.08.002
Huber N, Nix WD, Gao H (2002) Identification of elastic-plastic material parameters from pyramidal indentation of thin films. Proc R Soc A Math Phys Eng Sci 458:1593–1620. https://doi.org/10.1098/rspa.2001.0927
Hutchinson JW (2012) Generalizing J2 flow theory: fundamental issues in strain gradient plasticity. Acta Mech Sin Xuebao 28:1078–1086. https://doi.org/10.1007/s10409-012-0089-4
Idiart MI, Deshpande VS, Fleck NA, Willis JR (2009) Size effects in the bending of thin foils. Int J Eng Sci 47:1251–1264. https://doi.org/10.1016/j.ijengsci.2009.06.002
Jiang H, Huang Y, Zhuang Z, Hwang KC (2001) Fracture in mechanism-based strain gradient plasticity. J Mech Phys Solids 49:979–993. https://doi.org/10.1016/S0022-5096(00)00070-3
Kiser MT, Zok FW, Wilkinson DS (1996) Plastic flow and fracture of a particulate metal matrix composite. Acta Mater 44:3465–3476. https://doi.org/10.1016/1359-6454(96)00028-6
Kuroda M, Tvergaard V (2008) A finite deformation theory of higher-order gradient crystal plasticity. J Mech Phys Solids 56:2573–2584. https://doi.org/10.1016/j.jmps.2008.03.010
Lim YY, Munawar Chaudhri M (1999) The effect of the indenter load on the nanohardness of ductile metals: an experimental study onpolycrystalline work-hardened and annealed oxygen-free copper. Philos Mag A Phys Condens Matter Struct Defects Mech Prop 79:2979–3000. https://doi.org/10.1080/01418619908212037
Lloyd DJ (1994) Particle reinforced aluminium and magnesium matrix composites. Int Mater Rev 39:1–23
Lü Y, Wang Q, Zeng X et al (2000) Effects of rare earths on the microstructure, properties and fracture behavior of Mg-Al alloys. Mater Sci Eng, A 278:66–76. https://doi.org/10.1016/S0921-5093(99)00604-8
Lubarda VA (2017) On the analysis of pure bending of rigid-plastic beams in strain-gradient plasticity. Eur J Mech A/Solids 63:43–52. https://doi.org/10.1016/j.euromechsol.2016.12.001
Ma Q, Clarke DR (1995) Size dependent hardness of silver single crystals. J Mater Res 10:853–863. https://doi.org/10.1557/JMR.1995.0853
Mao YQ, Ai SG, Fang DN et al (2013) Elasto-plastic analysis of micro FGM beam basing on mechanism-based strain gradient plasticity theory. Compos Struct 101:168–179. https://doi.org/10.1016/j.compstruct.2013.01.027
McElhaney KW, Vlassak JJ, Nix WD (1998) Determination of indenter tip geometry and indentation contact area for depth-sensing indentation experiments. J Mater Res 13:1300–1306. https://doi.org/10.1557/JMR.1998.0185
Muhlhaus HB, Aifantis EC (1991) The influence of microstructure-induced gradients on the localization of deformation in viscoplastic materials. Acta Mech 89:231
Nan CW, Clarke DR (1996) The influence of particle size and particle fracture on the elastic/plastic deformation of metal matrix composites. Acta Mater 44:3801–3811. https://doi.org/10.1016/1359-6454(96)00008-0
Nix WD, Gao H (1998) Indentation size effects in crystalline materials: a law for strain gradient plasticity. J Mech Phys Solids 46:411–425. https://doi.org/10.1016/S0022-5096(97)00086-0
Park SK, Gao X-L (2006) Bernoulli-Euler beam model based on a modified couple stress theory. J Micromech Microeng 16:2355–2359. https://doi.org/10.1088/0960-1317/16/11/015
Patel BN, Pandit D, Srinivasan SM (2017) Large elaso-plastic deflection of micro-beams using strain gradient plasticity theory. Proc Eng 173:1064–1070. https://doi.org/10.1016/j.proeng.2016.12.186
Poole WJ, Ashby MF, Fleck NA (1996) Micro-hardness of annealed and work-hardened copper polycrystals. Scr Mater 34:559–564. https://doi.org/10.1016/1359-6462(95)00524-2
Rhee M, Hirth JP, Zbib HM (1994) A superdislocation model for the strengthening of metal matrix composites and the initiation and propagation of shear bands. Acta Metall Mater 42:2645–2655. https://doi.org/10.1016/0956-7151(94)90206-2
Shell De Guzman M, Neubauer G, Flinn P, Nix WD (1993) The role of indentation depth on the measured hardness of materials. MRS Proc 308:613. https://doi.org/10.1557/PROC-308-613
Shi MX, Huang Y, Hwang KC (2000) Plastic flow localization in mechanism-based strain gradient plasticity. Int J Mech Sci 42:2115–2131. https://doi.org/10.1016/S0020-7403(00)00009-6
Shi ZF, Huang B, Tan H et al (2008) Determination of the microscale stress-strain curve and strain gradient effect from the micro-bend of ultra-thin beams. Int J Plast 24:1606–1624. https://doi.org/10.1016/j.ijplas.2007.12.007
Stelmashenko NA, Walls MG, Brown LM, Milman YV (1993) Microindentations on W and Mo oriented single crystals: an STM study. Acta Metall Mater 41:2855–2865. https://doi.org/10.1016/0956-7151(93)90100-7
Stölken JS, Evans G (1998) A microbend test method for measuring the plasticity length scale. Acta Mater 46:5109–5115. https://doi.org/10.1016/S1359-6454(98)00153-0
Swadener J (2002) The correlation of the indentation size effect measured with indenters of various shapes. J Mech Phys Solids 50:681–694. https://doi.org/10.1016/S0022-5096(01)00103-X
Taylor MB, Zbib HM, Khaleel MA (2002) Damage and size effect during superplastic deformation. Int J Plast 18:415–442. https://doi.org/10.1016/S0749-6419(00)00106-6
Wang W, Huang Y, Hsia KJ et al (2003) A study of microbend test by strain gradient plasticity. Int J Plast 19:365–382. https://doi.org/10.1016/S0749-6419(01)00066-3
Xiang Y, Vlassak JJ (2006) Bauschinger and size effects in thin-film plasticity. Acta Mater 54:5449–5460. https://doi.org/10.1016/j.actamat.2006.06.059
Xue Z, Huang Y, Hwang KC, Li M (2002a) The Influence of Indenter Tip Radius on the Micro-Indentation Hardness. J Eng Mater Technol 124:371. https://doi.org/10.1115/1.1480409
Xue Z, Huang Y, Li M (2002b) Particle size effect in metallic materials: a study by the theory of mechanism-based strain gradient plasticity. Acta Mater 50:149–160. https://doi.org/10.1016/S1359-6454(01)00325-1
Zhou L, Li S, Huang S (2011) Simulation of effects of particle size and volume fraction on Al alloy strength, elongation, and toughness by using strain gradient plasticity concept. Mater Des 32:353–360. https://doi.org/10.1016/j.matdes.2010.06.026
Zhu HT, Zbib HM, Aifantis EC (1997) Strain gradients and continuum modeling of size effect in metal matrix composites. Acta Mech 176:165–176
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Darvishvand, A., Zajkani, A. A new model for permanent flexural deflection of cantilever MEMS actuator by conventional mechanism-based strain gradient plasticity framework. Microsyst Technol 25, 4277–4289 (2019). https://doi.org/10.1007/s00542-019-04337-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00542-019-04337-y