Skip to main content
Springer Nature Link
Log in

Nuclear reactor with subdiffusive neutron transport: development of linear fractional-order models

  • Published:
International Journal of Dynamics and Control Aims and scope Submit manuscript

Abstract

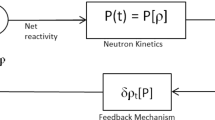
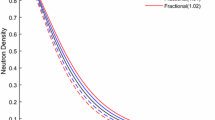
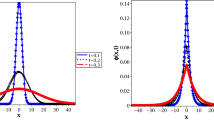
This paper deals with fractional-order (FO) modeling of a nuclear reactor. Modeling neutron transport in a nuclear reactor as subdiffusion results in the development of FO neutron telegraph equation. This model predicts subdiffusive behaviour for long-time. This fact is used to develop various linear control-oriented FO models for nuclear reactor. Development and analysis of three FO linear models is reported: FO point reactor kinetics model, Zero power FO transfer function and FO transfer function with temperature feedback of reactivity. In addition to the detailed stability analysis of these FO models, a comparative study of time-domain indices is carried out with respective integer-order models. The proposed FO models give a better representation of the neutron transport in the heterogeneous reactor core and therefore can be used to develop better model-based control strategies for a nuclear reactor.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Duderstadt JJ, Hamilton LJ (1976) Nuclear reactor analysis. Wiley, New York

    Google Scholar 

  2. Glasstone S, Sesonske A (2002) Nuclear reactor engineering, vol 1. CBS Publishers & Distributors, New Delhi

    Google Scholar 

  3. Lamarsh JR (1966) Introduction to nuclear reactor theory. Addison-Wesley Publishing Company, Boston

    Google Scholar 

  4. Vyawahare VA, Nataraj PSV (2013) Fractional-order modeling of neutron transport in a nuclear reactor. Appl Math Model 37:9747–9767

    Article  MathSciNet  Google Scholar 

  5. Espinosa-Paredes G, Morales-Sandoval JB, Vázquez-Rodríguez R, Espinosa-Martínez EG (2008) Constitutive laws for the neutron transport current. Ann Nucl Energy 35:1963–1967

    Article  Google Scholar 

  6. Klages R, Radons G, Sokolov IM (eds) (2008) Anomalous transport. WILEY-VCH Verlag GmbH & Co, New York

    Google Scholar 

  7. Metzler R, Klafter J (2000) The random walk’s guide to anomalous diffusion: a fractional dynamics approach. Phys Rep 339:1–77

    Article  MATH  MathSciNet  Google Scholar 

  8. Espinosa-Paredes G, Polo-Labarrios MA (2012) Time-fractional telegrapher’s equation (P1) approximation for the transport equation. Nucl Sci Eng J 171:258–264

    Article  Google Scholar 

  9. Compte A, Metzler R (1997) The generalized Cattaneo equation for the description of anomalous transport processes. J Phys A Math Gen 30:7277–7289

    Article  MATH  MathSciNet  Google Scholar 

  10. Meghreblian RV, Holmes DK (1960) Reactor analysis. McGraw-Hill Book Company, New York

    Google Scholar 

  11. Samko SG, Kilbas AA, Marichev OI (1997) Fractional integrals and derivatives. Gordon and Breach Science Publishers, Amsterdam

    MATH  Google Scholar 

  12. Das S (2011) Functional fractional calculus for system identification and controls. Springer, Berlin

    Book  Google Scholar 

  13. Magin RL (2006) Fractional calculus in bioengineering. Begell House Publishers, Danbury

    Google Scholar 

  14. Arafa AAM, Rida SZ, Khalil M (2014) A fractional-order model of HIV infection with drug therapy effect. J Egypt Math Soc 22(3):538–543

    Article  MATH  MathSciNet  Google Scholar 

  15. Freeborn TJ (2013) A survey of fractional-order circuit models for biology and biomedicine. IEEE J Emerg Sel Top Circuits Syst 3(3):416–424

    Article  Google Scholar 

  16. Grzesikiewicz W, Wakulicz A, Zbiciak A (2013) Non-linear problems of fractional calculus in modeling of mechanical systems. Int J Mech Sci 70:90–98

    Article  Google Scholar 

  17. Lino P, Maione G, Saponaro F (2015) Fractional-order modeling of high-pressure fluid-dynamic flows: an automotive application. In: 8th Vienna international conference on mathematical modelling, Vienna

  18. Freeborn TJ, Maundy B, Elwakil AS (2015) Fractional-order models of supercapacitors, batteries and fuel cells: a survey. Mater Renew Sustain Energy 4–9:1–7

    Google Scholar 

  19. Jalloul A, Trigeassou JC, Jelassi K, Melchior P (2013) Fractional order modeling of rotor skin effect in induction machines. Nonlinear Dyn 73(1):801–813

    Article  Google Scholar 

  20. Zheng W, Luo Y, Chen YQ, Pi YG (2016) Fractional-order modeling of permanent magnet synchronous motor speed servo system. J Vib Control 22(9):2255–2280

    Article  Google Scholar 

  21. Chen-Charpentier B, González-Parra G, Arenas AJ (2015) Fractional order financial models for awareness and trial advertising decisions. Comput Econ. doi:10.1007/s10614-015-9546-z

  22. Li Q, Zhou Y, Zhao X, Ge X (2014) Fractional order stochastic differential equation with application in european option pricing. Discrete Dyn Nat Soc 2014:1–12

    MathSciNet  Google Scholar 

  23. Wang Z, Huang X, Shi G (2011) Analysis of nonlinear dynamics and chaos in a fractional order financial system with time delay. Comput Math Appl Spec Issue Adv Fract Differ Equ II 62(3):1531–1539

    MATH  MathSciNet  Google Scholar 

  24. Mehdinejadiani B, Naseri AA, Jafari H, Ghanbarzadeh A, Baleanu D (2013) A mathematical model for simulation of a water table profile between two parallel subsurface drains using fractional derivatives. Comput Math Appl 66(5):785–794 Fractional Differentiation and its Applications

    Article  MATH  MathSciNet  Google Scholar 

  25. Monje CA, Chen YQ, Vinagre BM, Xue D, Feliu V (2010) Fractional-order systems and control: fundamentals and applications. Springer-Verlag London Limited, London

    Book  MATH  Google Scholar 

  26. Machado JT, Kiryakova V, Mainardi F (2011) Recent history of fractional calculus. Commun Nonlinear Sci Numer Simul 16(3):1140–1153

    Article  MATH  MathSciNet  Google Scholar 

  27. Das S, Biswas BB (2007) Fractional divergence for neutron flux profile in nuclear reactor. Int J Nucl Energy Sci Technol 3(2):139–159

    Article  Google Scholar 

  28. Das S, Das S, Gupta A (2011) Fractional order modeling of a PHWR under step-back condition and control of its global power with a robust \({P} {I}^\lambda {D}^\mu \) controller. IEEE Trans Nucl Sci 58(5):2431–2441

    Article  Google Scholar 

  29. Kadem A, Baleanu D (2010) Analytical method based on Walsh function combined with orthogonal polynomial for fractional transport equation. Commun Nonlinear Sci Numer Simul 15(3):491–501

    Article  MATH  MathSciNet  Google Scholar 

  30. Kadem A, Baleanu D (2012) Two-dimensional transport equation as Fredholm integral equation. Commun Nonlinear Sci Numer Simul 17(2):530–535

    Article  MATH  MathSciNet  Google Scholar 

  31. Sardar T, Ray SS, Bera R, Biswas B, Das S (2010) The solution of coupled fractional neutron diffusion equations with delayed neutrons. Int J Nucl Energy Sci Technol 5(2):105–113

    Article  Google Scholar 

  32. Hetrick DL (1993) Dynamics of nuclear reactors. American Nuclear Society, La Grange Park

    Google Scholar 

  33. Henry AF (1970) Nuclear reactor analysis. The MIT Press, Cambridge

    Google Scholar 

  34. Stacey WM (2007) Nuclear reactor physics. WILEY-VCH Verlag GmbH & Co., New York

    Book  Google Scholar 

  35. Alcouffe RE, Larsen EW, Miller WF Jr, Wienke BR (1979) Computational efficiency of numerical methods for the multigroup, discrete-ordinates neutron transport equations: the slab geometry case. Nucl Sci Eng 71(2):111–127

    Article  Google Scholar 

  36. Kadem A, Baleanu D (2010) \({F}_{N}\) approximation to fractional neutron transport equation in slab geometry. Paper appeared in the proceedings of international conference on the new trends in nanotechnology and nonlinear dynamical systems, Ankara, Turkey, 25–27 July 2010

  37. Lee CE (1986) Analytic solutions of the multigroup space-time reactor kinetics equations-I: 1-D multiregion slab and spherical geometry. Ann Nucl Energy 13(5):245–268

    Article  Google Scholar 

  38. Mullikin TW (1962) Estimates of critical dimensions of spherical and slab reactors. J Math Anal Appl 5(2):184–199

    Article  MATH  MathSciNet  Google Scholar 

  39. Espinosa-Paredes G, Polo-Labarrios MA, Espinosa-Martínez EG, del Valle-Gallegos E (2011) Fractional neutron point kinetics equations for nuclear reactor dynamics. Ann Nucl Energy 38:307–330

    Article  Google Scholar 

  40. Nowak TK, Duzinkiewicz K, Piotrowski R (2014) Fractional neutron point kinetics equations for nuclear reactor dynamics numerical solution investigations. Ann Nucl Energy 73:317–329

    Article  MATH  Google Scholar 

  41. Nowak TK, Duzinkiewicz K, Piotrowski R (2014) Numerical solution of fractional neutron point kinetics model in nuclear reactor. Arch Control Sci 24(2):129–154

    MATH  MathSciNet  Google Scholar 

  42. Ray SS, Patra A (2012) An Explicit finite difference scheme for numerical solution of fractional neutron point kinetic equation. Ann Nucl Energy 41:61–66

    Article  Google Scholar 

  43. Espinosa-Paredes G, del Valle-Gallegos E, Núñez-Carrera A, Polo-Labarrios MA, Espinosa-Martínez EG, Vázquez-Rodríguez A (2014) Fractional neutron point kinetics equation with Newtonian temperature feedback effects. Prog Nucl Energy 73:96–101

    Article  Google Scholar 

  44. Polo-Labarrios MA, Espinosa-Martínez EG, Quezada-García S, Varela-Ham JR, Espinosa-Paredes G (2014) Fractional neutron point kinetic equation with ramp and sinusoidal reactivity effects. Ann Nucl Energy 72:90–94

    Article  Google Scholar 

  45. Ray SS, Patra A (2013) Numerical solution of fractional stochastic neutron point kinetic equation for nuclear reactor dynamics. Ann Nucl Energy 54:154–161

    Article  Google Scholar 

  46. Polo-Labarrios MA, Espinosa-Paredes G (2012) Application of the fractional neutron point kinetic equation: start-up of a nuclear reactor. Ann Nucl Energy 46:37–42

    Article  Google Scholar 

  47. Polo-Labarrios MA, Espinosa-Paredes G (2012) Numerical analysis of startup PWR with fractional neutron point kinetic equation. Prog Nucl Energy 60:38–46

    Article  Google Scholar 

  48. Schramm M, Bodmann B, Alvim A, Vilhena M (2016) The neutron point kinetics equation: suppression of fractional derivative effects by temperature feedback. Ann Nucl Energy 87(2):479–485

    Article  MATH  Google Scholar 

  49. Schramm M, Petersen CZ, Vilhena MT, Bodmann BEJ, Alvim A (2013) On the fractional neutron point kinetics equations. In: Constanda C, Bodmann BEJ, de Campos Velho HF (eds) Integral methods in science and engineering. Springer, New York, pp 229–243

    Chapter  Google Scholar 

  50. Farlow S (2004) Partial differential equations. Dover Publishing Company, Mineola

    MATH  Google Scholar 

  51. Logan JD (2004) Partial differential equations. Springer, New York

    MATH  Google Scholar 

  52. Rudin W (2006) Principles of mathematical analysis. Tata McGraw-Hill Company, Delhi

    MATH  Google Scholar 

  53. Gorenflo R, Loutchko J, Luchko Y (2002) Computation of the Mittag–Leffler function \({E}_{\alpha, \beta }(z)\) and its derivative. Fract Calc Appl Anal 5(4):491–518

    MATH  MathSciNet  Google Scholar 

  54. Podlubny I (1999) Fractional differential equations. Academic Press, Cambridge

    MATH  Google Scholar 

  55. Odibat ZM (2010) Analytic study of linear systems of fractional differential equations. Comput Math Appl 59:1171–1183

    Article  MATH  MathSciNet  Google Scholar 

  56. Sheng H, Li Y, Chen YQ (2010) Application of numerical inverse Laplace transform algorithms in fractional calculus. In: The 4th IFAC workshop on fractional differentiation and its applications, Badajoz

  57. Podlubny I (2005) Mittag–Leffler function—file exchange—MATLAB Central. http://www.mathworks.com/matlabcentral/fileexchange/8738

  58. Mohler RR, Shen CN (1970) Optimal control of nuclear reactors. Academic Press, Cambridge

    Google Scholar 

  59. Nahla AA (2011) Taylor’s series method for solving the nonlinear point kinetics equations. Nucl Eng Design 241:1592–1595

    Article  Google Scholar 

  60. Cammi A, Di-Marcello V, Guerrieri C, Luzzi L (2011) Transfer function modeling of zero-power dynamics of circulating fuel reactors. J Eng Gas Turbines Power 133(5):52916–52923

    Article  Google Scholar 

  61. Damen PMG, Kloosterman JL (2001) Dynamics aspects of plutonium burning in an inert matrix. Prog Nucl Energy 38(3–4):371–374

    Article  Google Scholar 

  62. Yi TT, Koshizuka S, Oka Y (2004) A linear stability analysis of supercritical water reactors: (I) coupled neutronic thermal-hydraulic stability. J Nucl Sci Technol 41(12):1166–1175

    Article  Google Scholar 

  63. Yi TT, Koshizuka S, Oka Y (2004) A linear stability analysis of supercritical water reactors: (II) coupled neutronic thermal-hydraulic stability. J Nucl Sci Technol 41(12):1176–1186

    Article  Google Scholar 

  64. Ogata K (2002) Modern control engineering. Prentice-Hall, New Delhi

    MATH  Google Scholar 

  65. Vyawahare VA, Nataraj PSV (2013) Development and analysis of some versions of the fractional-order point reactor kinetics model for a nuclear reactor with slab geometry. Commun Nonlinear Sci Numer Simul 18:1840–1856

    Article  MATH  MathSciNet  Google Scholar 

  66. LePage WR (2010) Complex variables and the laplace transform for engineers. Dover Publications, Mineola

    Google Scholar 

  67. Radwan AG, Soliman AM, Elwakil A, Sedeek A (2009) On the stability of linear systems with fractional-order elements. Chaos Solitons Fractals 40:2317–2328

    Article  MATH  Google Scholar 

  68. Nahla AA (2009) An analytical solution for the point reactor kinetics equations with one group of delayed neutrons and the adiabatic feedback model. Prog Nucl Energy 51:124–128

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Electronics Engineering, Ramrao Adik Institute of Technology, Nerul, Navi Mumbai, India

    Vishwesh A. Vyawahare

  2. IDP in Systems and Control Engineering, Indian Institute of Technology Bombay, Powai, Mumbai, India

    P. S. V. Nataraj

  3. Área de Ingenierí en Recursos Energéticos, Universidad Autónoma Metropolitana-Iztapalapa, Av. San Rafael Atlixco 186, Col. Vicentina, Mexico, D.F., 09340, Mexico

    G. Espinosa-Paredes

  4. División de Ciencias Básica e Ingeniería, División de Ciencias y Biológicas de la Salud, Universidad Autónoma Metropolitana-Iztapalapa, Av. San Rafael Atlixco 186, Col. Vicentina, Mexico, D.F., 09340, Mexico

    R.-I. Cázares-Ramírez

Authors
  1. Vishwesh A. Vyawahare
    View author publications

    Search author on:PubMed Google Scholar

  2. P. S. V. Nataraj
    View author publications

    Search author on:PubMed Google Scholar

  3. G. Espinosa-Paredes
    View author publications

    Search author on:PubMed Google Scholar

  4. R.-I. Cázares-Ramírez
    View author publications

    Search author on:PubMed Google Scholar

Corresponding author

Correspondence to Vishwesh A. Vyawahare.

Additional information

A preliminary version of this paper was presented at The Fifth Symposium on Fractional Differentiation and its Applications (FDA’12), held at Hohai University, Nanjing, China, between 14 and 17 May, 2012.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Vyawahare, V.A., Nataraj, P.S.V., Espinosa-Paredes, G. et al. Nuclear reactor with subdiffusive neutron transport: development of linear fractional-order models. Int. J. Dynam. Control 5, 1182–1200 (2017). https://doi.org/10.1007/s40435-016-0272-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40435-016-0272-8

Keywords