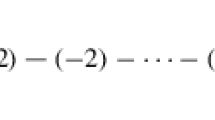Abstract
We give explicit formulas for the Gaussian curvature and other differential geometric functions of a holomorphic curve in complex projective space. It is proved that the curve is uniquely determined by these functions up to an isometry of the ambient space.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
GRIFFITHS, P.: On Cartan's method of Lie groups and moving frames as applied to uniqueness and existence questions in differential geometry. Duke J. Math.41, 775–814 (1974)
GRIFFITHS, P. and J. HARRIS: Algebraic geometry and local differential geometry. Ann. scient. Éc. Norm. Sup.12, 355–432 (1979)
KOBAYASHI, S. and K. NOMIZU: Foundations of differential geometry, Vol. I and II, Interscience, New York, 1963 and 1969
NESS, L.: Curvature on algebraic plane curves I. Comp. Math.35, 57–63 (1977)
NOMIZU, K. and B. SMYTH: Differential geometry of complex hypersurfaces II. J. Math. Soc. Japan,20, 498–521 (1968)
PIENE, R.: Numerical characters of a curve in projective n-space. Real and complex singularities, Sijthoff & Noordhof, Oslo, 1976
VITTER, A.: On the curvature of complex hypersurfaces. Indiana U. Math. J.,23, 813–826 (1974)
Weyl, H.: Meromorphic functions and analytic curves. Annals of Mathematics Studies 12, Princeton University Press, 1943
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Fischer, G. Differential geometry of complex projective space curves. Manuscripta Math 45, 47–59 (1983). https://doi.org/10.1007/BF01168579
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF01168579