Fracture in strain gradient elasticity

Abstract

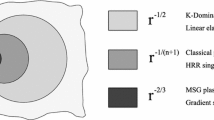
Recent experiments have shown that the microscale material behavior is very different from that of bulk materials, and displays strong size effects when the characteristic length associated with the deformation is on the order of microns. Conventional continuum theories, however, can not predict this size dependence because they do not have an intrinsic length in their constitutive models. A new continuum theory, namely the strain gradient theory, has been proposed to investigate the deformation of solids at the microscale. For materials undergoing plastic deformation, the basis of strain gradient theory is the dislocation theory in materials science, and strain gradient plasticity has agreed remarkably well with experiments. For elastic materials with microstructures, it has also been established that the material behavior can be represented by an elastic strain gradient theory. A general approach to investigate fracture of materials with strain gradient effects is established. Both the near-tip asymptotic fields and the elastic full-field solutions are obtained in closed form. Due to stain gradient effects, stresses ahead of a crack tip are significantly higher than those in the classical K field. The plastic zone size surronunding a crack tip is estimated by elastic near-tip fields, as well as by the Dugdale model. It is established that the plastic zone is, in general, much more round and larger than that estimated from the classical K field.