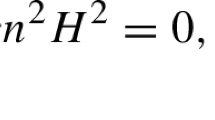Skip to main content
Springer Nature Link
Log in

Biharmonic hypersurfaces in Euclidean space E 5

  • Published:
Journal of Geometry Aims and scope Submit manuscript

Abstract

In this paper, we study biharmonic hypersurfaces in E 5. We prove that every biharmonic hypersurface in Euclidean space E 5 must be minimal.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Arvanitoyeorgos A., Defever F., Kaimakamis G., Papantoniou V.: Biharmonic Lorentzian hypersurfaces in \({E_{1}^{4}}\). Pac. J. Math. 229(2), 293–305 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  2. Chen B.Y.: Some open problems and conjectures on submanifolds of finite type. Soochow J. Math. 17(2), 169–188 (1991)

    MathSciNet  MATH  Google Scholar 

  3. Chen B.Y.: Total Mean Curvature and Submanifolds of Finite Type, 2nd edn. World Scientific, Hackensack, NJ (2014)

    Book  Google Scholar 

  4. Chen B.Y.: Classification of marginally trapped Lorentzian flat surfaces in \({E_{1}^{4}}\) and its application to biharmonic surfaces. J. Math. Anal. Appl. 340, 861–875 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  5. Chen B.Y., Ishikawa S.: Biharmonic surfaces in pseudo-Euclidean spaces. Mem. Fac. Sci. Kyushu Univ. A 45, 323–347 (1991)

    MathSciNet  MATH  Google Scholar 

  6. Chen B.Y., Ishikawa S.: Biharmonic pseudo-Riemannian submanifolds in pseudo-Euclidean spaces, Kyushu J. Math. 52, 1–18 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  7. Chen B.Y., Munteanu M.I.: Biharmonic ideal hypersurfaces in Euclidean spaces. Differ. Geom. Appl. 31, 1–16 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  8. Deepika., Gupta R.S.: Biharmonic hypersurfaces in E 5 with zero scalar curvature. Afr. Diaspora J. Math. 18(1), 12–26 (2015)

    MathSciNet  MATH  Google Scholar 

  9. Deepika., Gupta, R.S., Sharfuddin, A.: Biharmonic hypersurfaces with constant scalar curvature in \({E_{s}^{5}}\), Kyungpook Math. J., (accepted)

  10. Defever F., Kaimakamis G., Papantoniou V.: Biharmonic hypersurfaces of the 4-dimensional semi-Euclidean space \({E_{s}^{4}}\). J. Math. Anal. Appl. 315, 276–286 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  11. Dimitric, I.: Quadric representation and submanifolds of finite type, Doctoral thesis. Michigan State University (1989)

  12. Dimitric I.: Submanifolds of E n with harmonic mean curvature vector. Bull. Inst. Math. Acad. Sinica 20, 53–65 (1992)

    MathSciNet  MATH  Google Scholar 

  13. Akutagawa K., Maeta S.: Biharmonic properly immersed submanifolds in Euclidean spaces. Geom. Dedicate 164, 351–355 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  14. Hasanis T., Vlachos T.: Hypersurfaces in \({E^{4}}\) with harmonic mean curvature vector field. Math. Nachr. 172, 145–169 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  15. Gupta R.S.: On biharmonic hypersurfaces in Euclidean space of arbitrary dimension. Glasgow Math. J. Glasgow Math. J. 57, 633–642 (2015)

    Article  MATH  Google Scholar 

  16. Gupta, R.S.: Biharmonic hypersurfaces in \({E_{s}^{5}}\), An. St. Univ. Al. I. Cuza, (accepted)

  17. Fu Y.: Biharmonic hypersurfaces with three distinct principal curvatures in the Euclidean 5-space. J. Geometr. Phys. 75, 113–119 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  18. Fu Y.: On biharmonic hypersurfaces with constant scalar curvatures in \({\mathbb{S}^{5}}\). Proc. Am. Math. Soc. 143, 5399–5409 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  19. Fu Y.: Biharmonic hypersurfaces with three distinct principal curvatures in Euclidean space. Tohoku Math. J. (2) 67(3), 465–479 (2015)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. University School of Basic and Applied Sciences, Guru Gobind Singh Indraprastha University, Sector-16C, Dwarka, New Delhi, 110078, India

    Ram Shankar Gupta

  2. Department of Mathematics, Faculty of Natural Sciences, Jamia Millia Islamia (Central University), New Delhi, 110025, India

    A. Sharfuddin

Authors
  1. Ram Shankar Gupta
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. A. Sharfuddin
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Ram Shankar Gupta.

Additional information

This work started while first author was on depuation as Associate Professor, Department of Mathematics, Central University of Jammu, Sainik colony, Jammu-180011, India.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gupta, R.S., Sharfuddin, A. Biharmonic hypersurfaces in Euclidean space E 5 . J. Geom. 107, 685–705 (2016). https://doi.org/10.1007/s00022-015-0310-2

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00022-015-0310-2

Mathematics Subject Classification

Keywords