Analysis of shear rheometry of yield stress materials and apparent yield stress materials

Abstract.

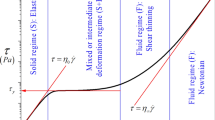
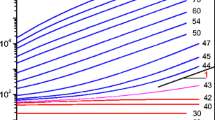
For the most common types of viscometers the apparent flow curve of plastic fluids is studied. For torsional flow, where the shear rate is the natural variable, the apparent yield stress exceeds the true yield stress $\tau _c$ by more than 33%. If, on the other hand, $\tau$ is the natural variable (like in capillary flow, slit flow, and concentric cylinder flow) the yield stress is correctly predicted, but the behavior close to $\tau _c$ differs fundamentally. If the apparent shear rate $\dot \gamma _a$ goes to zero like $\left( {\tau - \tau _c } \right)^{1/n}$ (where the power law index n could be the power law index of a Herschel-Bulkley fluid), the true shear rate has to be proportional to $\left( {\tau - \tau _c } \right)^{\left[ {1/n} \right] - 1}$ for $\tau \to \tau _c$ . For n=1 this implies a discontinuity of $\dot \gamma$ at $\tau _c$ ($\dot \gamma = 0$ for $\tau < \tau _c$ ). For tangential annular flow between concentric cylinders the ratio of radii $\left( \kappa \right)$ enters. Using an exact relation between $\dot \gamma$ and $\dot \gamma _a$ reveals that no single (κ-dependent) expression for the apparent flow curve can exist, which would for plastic fluids cover the entire flow regime ($\tau > \tau _c$ ). Irrespective as to what viscometer is used the far field behavior of the apparent flow curve and the true flow curve will, in general, differ too, though only quantitatively.