Skip to main content

Advertisement

Springer Nature Link
Log in

Artificial neural network approach for a class of fractional ordinary differential equation

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

Abstract

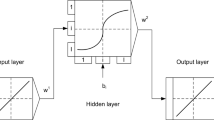
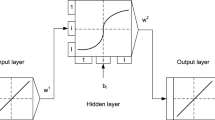
The essential characteristic of artificial neural networks which against the logistic traditional systems is a data-based approach and has led a number of higher education scholars to investigate its efficacy, during the past few decades. The aim of this paper was concerned with the application of neural networks to approximate series solutions of a class of initial value ordinary differential equations of fractional orders, over a bounded domain. The proposed technique uses a suitable truncated power series of the solution function and transforms the original differential equation in a minimization problem. Then, the minimization problem is solved using an accurate neural network model to compute the parameters with high accuracy. Numerical results are given to validate the iterative method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Baleanu D, Diethelm K, Scalas E, Trujillo JJ (2012) Fractional calculus models and numerical methods. Series on complexity, nonlinearity and chaos, World Scientific, Boston

  2. Bandyopadhyay B, Kamal S (2015) Stabilization and control of fractional order systems: a sliding mode approach, vol 317. Springer, Switzerland

    MATH  Google Scholar 

  3. Ervin VJ, Roop JP (2005) Variational formulation for the stationary fractional advection dispersion equation. Numer Methods Partial Differ Equ 22:558–576

    Article  MathSciNet  MATH  Google Scholar 

  4. Gejji VD, Jafari H (2007) Solving a multi-order fractional differential equation. Appl Math Comput 189:541–548

    MathSciNet  MATH  Google Scholar 

  5. Graupe D (2007) Principles of artificial neural networks, 2nd edn. World Scientific Publishing, Singapore

    Book  MATH  Google Scholar 

  6. Hanss M (2005) Applied Fuzzy arithmetic: an introduction with engineering applications. Springer, Berlin

    MATH  Google Scholar 

  7. Hassoun MH (1995) Fundamentals of artificial neural networks. MIT Press, Cambridge

    MATH  Google Scholar 

  8. He JH, Shou DH (2007) Application of parameter-expanding method to strongly nonlinear oscillators. Int J Nonlinear Sci Numer Simul 8:121–124

    Article  Google Scholar 

  9. Jumarie G (2006) Modified Riemann–Liouville derivative and fractional Taylor series of nondifferentiable functions further results. Comput Math Appl 51:969–987

    Article  MathSciNet  MATH  Google Scholar 

  10. Kilbas AA, Srivastava HM, Trujillo JJ (2006) Theory and applications of fractional differential equations. In: Jan Van Mill (ed) North-Holland mathematics studies, vol 204, Elsevier, Netherland

  11. Lakshmikantham V, Leela S, Vasundhara Devi J (2009) Theory of fractional dynamic systems. Cambridge University Press, Cambridge

    MATH  Google Scholar 

  12. Momani S, Odibat Z (2007) Numerical comparison of methods for solving linear differential equations of fractional order. Chaos Solitons Fractals 31(5):1248–1255

    Article  MathSciNet  MATH  Google Scholar 

  13. Momani S, Odibat Z (2007) Comparison between homotopy perturbation method and the variational iteration method for linear fractional partial differential equations. Comput Math Appl. doi:10.1016/j.camwa.2006.12.037

  14. Odibat Z, Momani S (2006) Application of variational iteration method to nonlinear differential equations of fractional order. Int J Nonlinear Sci Numer Simul 7(1):15–27

    Article  MathSciNet  Google Scholar 

  15. Sabatier J, Agrawal OP, Machado JAT (eds) (2007) Advances in fractional calculus: theoretical developments and applications in physics and engineering. Springer, Dordrecht

    MATH  Google Scholar 

  16. Sweilam NH, Khader MM, Al-Bar RF (2007) Numerical studies for a multi-order fractional differential equation. Phys Lett A 371:26–33

    Article  MathSciNet  MATH  Google Scholar 

  17. Wang Y, Fan Q (2012) The second kind Chebyshev wavelet method for solving fractional differential equations. Appl Math Comput 218:8592–8601

    MathSciNet  MATH  Google Scholar 

  18. Yang XJ (2012) Advanced local fractional calculus and its applications. World Science Publisher, New York

    Google Scholar 

  19. Yildirim A, Kocak H (2009) Homotopy perturbation method for solving the space-time fractional advection-dispersion equation. Adv Water Resour 32:1711–1716

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Urmia Branch, Islamic Azad University, Urmia, Iran

    Ahmad Jafarian & Masoumeh Mokhtarpour

  2. Department of Mathematics, Cankaya University, Eskisehir Yolu 29 km, 06810, Ankara, Turkey

    Dumitru Baleanu

  3. Institute of Space Sciences, Magurele, Bucharest, Romania

    Dumitru Baleanu

Authors
  1. Ahmad Jafarian
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Masoumeh Mokhtarpour
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Dumitru Baleanu
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Dumitru Baleanu.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jafarian, A., Mokhtarpour, M. & Baleanu, D. Artificial neural network approach for a class of fractional ordinary differential equation. Neural Comput & Applic 28, 765–773 (2017). https://doi.org/10.1007/s00521-015-2104-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-015-2104-8

Keywords