Skip to main content
Springer Nature Link
Log in

Size-dependent shear buckling response of FGM skew nanoplates modeled via different homogenization schemes

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

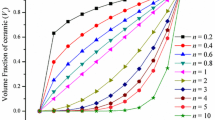
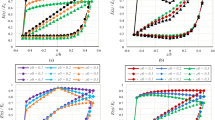
The size effects on the shear buckling behaviors of skew nanoplates made of functionally graded materials (FGMs) are presented. The material properties are supposed to be changed uniformly from the ceramic phase to the metal one along the plate thickness. To estimate the associated effective material properties, various homogeniza-tion schemes including the Reuss model, the Voigt model, the Mori-Tanaka model, and the Hashin-Shtrikman bound model are used. The nonlocal elasticity theory together with the oblique coordinate system is applied to the higher-order shear deformation plate theory to develop a size-dependent plate model for the shear buckling analysis of FGM skew nanoplates. The Ritz method using Gram-Schmidt shape functions is used to solve the size-dependent problem. It is found that the significance of the nonlocality in the reduction of the shear buckling load of an FGM skew nanoplate increases for a higher value of the material property gradient index. Also, by increasing the skew angle, the critical shear buckling load of an FGM skew nanoplate enhances. This pattern becomes a bit less significant for a higher value of the material property gradient index. Furthermore, among various homogenization models, the Voigt and Reuss models in order estimate the overestimated and underestimated shear buckling loads, and the difference between them reduces by increasing the aspect ratio of the skew nanoplate.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. BHARILYA, R. K. and PUROHIT, R. Application of functionally graded nano material (FGNM) laminates for solenoid based actuators. Materials Today: Proceedings, 5, 20736–20740 (2017)

    Google Scholar 

  2. VABEN, R., RAUWALD, K. H., GUILLON, O., AKTAA, J., WEBER, T., BACK, H. C., QU, D., and GIBMEIER, J. Vacuum plasma spraying of functionally graded tungsten/EUROFER97 coatings for fusion applications. Fusion Engineering and Design, 133, 148–156 (2017)

    Google Scholar 

  3. SMITH, J. A., MELE, E., RIMINGTON, R. P., CAPEL, A. J., LEWIS, M. P., SILBER-SCHMIDT, V. V., and LI, S. Polydimethylsiloxane and poly(ether) ether ketone functionally graded composites for biomedical applications. Journal of the Mechanical Behavior of Biomedical Materials, 93, 130–142 (2017)

    Google Scholar 

  4. QI, L. Energy harvesting properties of the functionally graded flexoelectric microbeam energy harvesters. Energy, 171, 721–730 (2017)

    Google Scholar 

  5. SHAH, A. T., ZAHID, S., IKRAM, F., MAQBOOL, M., CHAUDHRY, A. A., RAHIM, M. I., SCHMIDT, F., KHAN, A. S., AND REHMAN, I. U. Tri-layered functionally graded membrane for potential application in periodontal regeneration. Materials Science and Engineering: C, 103, 109812 (2019)

    Google Scholar 

  6. LIU, H., DING, S., and NG, B. F. Impact response and energy absorption of functionally graded foam under temperature gradient environment. Composites Part B: Engineering, 172, 516–532 (2017)

    Google Scholar 

  7. SHOJAEIAN, M. and TADI-BENI, Y. Size-dependent electromechanical buckling of functionally graded electrostatic nano-bridges. Sensors and Actuators A: Physical, 232, 49–62 (2017)

    Google Scholar 

  8. AKBARZADEH, A. H., ABEDINI, A., and CHEN, Z. T. Effect of micromechanical models on structural responses of functionally graded plates. Composite Structures, 119, 598–609 (2017)

    Google Scholar 

  9. TAATI, E. Analytical solutions for the size dependent buckling and postbuckling behavior of functionally graded micro-plates. International Journal of Engineering Science, 100, 45–60 (2017)

    MathSciNet  MATH  Google Scholar 

  10. MEHRALIAN, F. and TADI-BENI, Y. Size-dependent torsional buckling analysis of functionally graded cylindrical shell. Composites Part B: Engineering, 94, 11–25 (2017)

    Google Scholar 

  11. LOU, J., HE, L., WU, H., and DU, J. Pre-buckling and buckling analyses of functionally graded microshells under axial and radial loads based on the modified couple stress theory. Composite Structures, 142, 226–237 (2017)

    Google Scholar 

  12. ZHANG, L. W., ZHANG, Y., and LIEW, K. M. Modeling of nonlinear vibration of graphene sheets using a meshfree method based on nonlocal elasticity theory. Applied Mathematical Modelling, 49, 691–704 (2017)

    MathSciNet  MATH  Google Scholar 

  13. ZHU, C. S., FANG, X. Q., and LIU, J. X. Surface energy effect on buckling behavior of the functionally graded nano-shell covered with piezoelectric nano-layers under torque. International Journal of Mechanical Sciences, 133, 662–673 (2017)

    Google Scholar 

  14. SHAFIEI, N. and KAZEMI, M. Buckling analysis on the bi-dimensional functionally graded porous tapered nano-/micro-scale beams. Aerospace Science and Technology, 66, 1–11 (2017)

    Google Scholar 

  15. THAI, S., THAI, H. T., VO, T. P., and REDDY, J. N. Post-buckling of functionally graded microplates under mechanical and thermal loads using isogeomertic analysis. Engineering Structures, 150, 905–917 (2017)

    Google Scholar 

  16. YANG, T., TANG, Y., LI, Q., and YANG, X. D. Nonlinear bending, buckling and vibration of bi-directional functionally graded nanobeams. Composite Structures, 204, 313–319 (2017)

    Google Scholar 

  17. SHAFIEI, N. and SHE, G. L. On vibration of functionally graded nano-tubes in thermal environment. International Journal of Engineering Science, 133, 84–98 (2017)

    MathSciNet  MATH  Google Scholar 

  18. AVRAMOV, K. V. Nonlinear vibrations characteristics of single-walled carbon nanotubes by nonlocal elastic shell model. International Journal of Non-Linear Mechanics, 107, 149–160 (2017)

    Google Scholar 

  19. CHU, L. and DUI, G. Exact solutions for functionally graded micro-cylinders in first gradient elasticity. International Journal of Mechanical Sciences, 148, 366–373 (2017)

    Google Scholar 

  20. JIAO, P., ALAVI, A. H., BORCHANI, W., and LAJNEF, N. Micro-composite films constrained by irregularly bilateral walls: a size-dependent post-buckling analysis. Composite Structures, 195, 219–231 (2017)

    Google Scholar 

  21. TAATI, E. On buckling and post-buckling behavior of functionally gradedmicro-beams in thermal environment. International Journal of Engineering Science, 128, 63–78 (2018)

    MathSciNet  MATH  Google Scholar 

  22. JIA, X. L., KE, L. L., ZHONG, X. L., SUN, Y., YANG, J., and KITIPORNCHAI, S. Thermal-mechanical-electrical buckling behavior of functionally graded micro-beams based on modified couple stress theory. Composite Structures, 202, 625–634 (2017)

    Google Scholar 

  23. RUOCCO, E., ZHANG, H., and WANG, C. M. Buckling and vibration analysis of nonlocal axially functionally graded nanobeams based on Hencky-bar chain model. Applied Mathematical Modelling, 63, 445–463 (2017)

    MathSciNet  Google Scholar 

  24. SARAFRAZ, A., SAHMANI, S., and AGHDAM, M. M. Nonlinear secondary resonance of nanobeams under subharmonic and superharmonic excitations including surface free energy effects. Applied Mathematical Modelling, 66, 195–226 (2017)

    MathSciNet  Google Scholar 

  25. TRABELSSI, M., EL-BORGI, S., FERNANDES, R., and KE, L. L. Nonlocal free and forced vibration of a graded Timoshenko nanobeam resting on a nonlinear elastic foundation. Composites Part B: Engineering, 157, 331–349 (2019)

    Google Scholar 

  26. KIM, J., ZUR, K. K., and REDDY, J. N. Bending, free vibration, and buckling of modified couples stress-based functionally graded porous micro-plates. Composite Structures, 209, 879–888 (2017)

    Google Scholar 

  27. KARAMI, B., SHAHSAVARI, D., JANGHORBAN, M., and LI, L. Influence of homogenization schemes on vibration of functionally graded curved microbeams. Composite Structures, 216, 67–79 (2017)

    Google Scholar 

  28. ARIA, A. I. and FRISWELL, M. I. A nonlocal finite element model for buckling and vibration of functionally graded nanobeams. Composites Part B: Engineering, 166, 233–246 (2017)

    Google Scholar 

  29. ZHU, X. and LI, L. Twisting statics of functionally graded nanotubes using Eringen’s nonlocal integral model. Composite Structures, 178, 87–96 (2017)

    Google Scholar 

  30. ROMANO, G., BARRETTA, R., DIACO, M., and MAROTTI DE SCIARRA, F. Constitutive boundary conditions and paradoxes in nonlocal elastic nanobeams. International Journal of Mechanical Sciences, 121, 151–156 (2017)

    Google Scholar 

  31. LI, L., LI, X., and HU, Y. Free vibration analysis of nonlocal strain gradient beams made of functionally graded material. International Journal of Engineering Science, 102, 77–92 (2017)

    MATH  Google Scholar 

  32. LU, L., ZHU, L., GUO, X. M., ZHAO, J. Z., and LIU, G. Z. A nonlocal strain gradient shell model incorporating surface effects for vibration analysis of functionally graded cylindrical nanoshells. Applied Mathematics and Mechanics (English Edition), 40(12), 1695–1722 (2019) https://doi.org/10.1007/s10483-019-2549-7

    MATH  Google Scholar 

  33. ZHU, X. and LI, L. A well-posed Euler-Bernoulli beam model incorporating nonlocality and surface energy effect. Applied Mathematics and Mechanics (English Edition), 40(11), 1561–1588 (2019) https://doi.org/10.1007/s10483-019-2541-5

    MathSciNet  MATH  Google Scholar 

  34. REDDY, J. N. and WANG, C. M. Deflection relationships between classical and third-order plate theories. Acta Mechanica, 130, 199–208 (2017)

    MathSciNet  MATH  Google Scholar 

  35. ERINGEN, A. C. Linear theory of nonlocal elasticity and dispersion of plane waves. International Journal of Engineering Science, 10, 425–435 (2017)

    MATH  Google Scholar 

  36. REUSS, A. Berechnung der fließgrenze von mischkristallen auf grund der plastizitätsbedingung für einkristalle. ZAMM-Journal of Applied Mathematics and Mechanics, 9, 49–58 (2017)

    MATH  Google Scholar 

  37. VOIGT, W. Ueber die beziehung zwischen den beiden elasticitätsconstanten isotroper körper. Annalen der Physik, 274, 573–587 (2017)

    MATH  Google Scholar 

  38. MORI, T. and TANAKA, K. Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metallurgica, 21, 571–574 (2017)

    Google Scholar 

  39. MISHNAEVSKY, Jr, J. Computational Mesomechanics of Composites, Wiley-Interscience, New York, 2979–2987 (2007)

    Google Scholar 

  40. ANITESCU, C., ATROSHCHENKO, E., ALAJLAN, N., and RABCZUK, T. Artificial neural network methods for the solution of second order boundary value problems. Computers, Materials and Continua, 59, 345–359 (2017)

    Google Scholar 

  41. RABCZUK, T., REN, H., and ZHUANG, X. A nonlocal operator method for partial differential equations with application to electromagnetic waveguide problem. Computers, Materials and Continua, 59, 31–55 (2017)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mechanical and Precision Instrument Engineering, Xi’an University of Technology, Xi’an, 710048, China

    Yuan Yuan & Ke Zhao

  2. School of Science and Technology, The University of Georgia, Tbilisi, 0171, Georgia

    S. Sahmani

  3. School of Mechanical Engineering, Eastern Mediterranean University, G. Magosa, TRNC Mersin 10, Turkey

    B. Safaei

Authors
  1. Yuan Yuan
    View author publications

    Search author on:PubMed Google Scholar

  2. Ke Zhao
    View author publications

    Search author on:PubMed Google Scholar

  3. S. Sahmani
    View author publications

    Search author on:PubMed Google Scholar

  4. B. Safaei
    View author publications

    Search author on:PubMed Google Scholar

Corresponding author

Correspondence to Yuan Yuan.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yuan, Y., Zhao, K., Sahmani, S. et al. Size-dependent shear buckling response of FGM skew nanoplates modeled via different homogenization schemes. Appl. Math. Mech.-Engl. Ed. 41, 587–604 (2020). https://doi.org/10.1007/s10483-020-2600-6

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10483-020-2600-6

Key words

Chinese Library Classification

2010 Mathematics Subject Classification