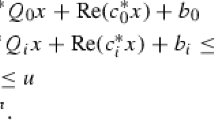Skip to main content

Advertisement

Springer Nature Link
Log in

Relaxing the optimality conditions of box QP

  • Published:
Computational Optimization and Applications Aims and scope Submit manuscript

Abstract

We present semidefinite relaxations of nonconvex, box-constrained quadratic programming, which incorporate the first- and second-order necessary optimality conditions, and establish theoretical relationships between the new relaxations and a basic semidefinite relaxation due to Shor. We compare these relaxations in the context of branch-and-bound to determine a global optimal solution, where it is shown empirically that the new relaxations are significantly stronger than Shor’s. An effective branching strategy is also developed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Anstreicher, K.M.: Semidefinite programming versus the reformulation-linearization technique for nonconvex quadratically constrained quadratic programming. J. Global Optim. 2, 471–484 (2009)

    Article  MathSciNet  Google Scholar 

  2. Burer, S., Vandenbussche, D.: Globally solving box-constrained nonconvex quadratic programs with semidefinite-based finite branch-and-bound. Comput. Optim. Appl. 2, 181–195 (2009)

    Article  MathSciNet  Google Scholar 

  3. De Angelis, P., Pardalos, P., Toraldo, G.: Quadratic programming with box constraints. In: Bomze, I.M., Csendes, T., Horst, R., Pardalos, P. (eds.) Developments in Global Optimization, pp. 73–94. Kluwer Academic, Norwell (1997)

    Google Scholar 

  4. Gould, N.I.M., Toint, P.L.: Numerical methods for large-scale non-convex quadratic programming. In: Trends in Industrial and Applied Mathematics, Amritsar, 2001. Appl. Optim., vol. 72, pp. 149–179. Kluwer Academic, Dordrecht (2002)

    Google Scholar 

  5. Horst, R., Tuy, H.: Global Optimization, second edition. Springer-Verlag, Berlin (1993). Deterministic Approaches

    Google Scholar 

  6. Löfberg Yalmip, J.: A toolbox for modeling and optimization in MATLAB. In: Proceedings of the CACSD Conference, Taipei, Taiwan (2004). URL http://control.ee.ethz.ch/~joloef/yalmip.php

  7. Nesterov, Y.: Global quadratic optimization via conic relaxation. In: Saigal, R., Vandenberghe, L., Wolkowicz, H. (eds.) Handbook of Semidefinite Programming, pp. 363–386. Kluwer Academic, Dordrecht (2000)

    Google Scholar 

  8. Pardalos, P.: Global optimization algorithms for linearly constrained indefinite quadratic problems. Comput. Math. Appl. 21, 87–97 (1991)

    Article  MATH  MathSciNet  Google Scholar 

  9. Pardalos, P.M., Vavasis, S.A.: Quadratic programming with one negative eigenvalue is NP-hard. J. Global Optim. 1(1), 15–22 (1991)

    Article  MATH  MathSciNet  Google Scholar 

  10. Sherali, H.D., Adams, W.P.: A Reformulation-Linearization Technique (RLT) for Solving Discrete and Continuous Nonconvex Problems. Kluwer Academic, Dordrecht (1997)

    Google Scholar 

  11. Shor, N.: Quadratic optimization problems. Sov. J. Comput. Syst. Sci. 25, 1–11 (1987). Originally published in Tekh. Kibern. 1, 128–139 (1987)

    MATH  MathSciNet  Google Scholar 

  12. Sturm, J.F.: Using SeDuMi 1.02, a MATLAB toolbox for optimization over symmetric cones. Optim. Methods Softw. 11/12(1–4), 625–653 (1999). URL http://sedumi.mcmaster.ca/

    Article  MathSciNet  Google Scholar 

  13. Vandenbussche, D., Nemhauser, G.: A polyhedral study of nonconvex quadratic programs with box constraints. Math. Program. 102(3), 531–557 (2005a)

    Article  MATH  MathSciNet  Google Scholar 

  14. Vandenbussche, D., Nemhauser, G.: A branch-and-cut algorithm for nonconvex quadratic programs with box constraints. Math. Program. 102(3), 559–575 (2005b)

    Article  MATH  MathSciNet  Google Scholar 

  15. Ye, Y.: Approximating quadratic programming with bound and quadratic constraints. Math. Program. 84(2, Ser. A), 219–226 (1999)

    MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Management Sciences, University of Iowa, Iowa City, IA, 52242-1994, USA

    Samuel Burer & Jieqiu Chen

Authors
  1. Samuel Burer
    View author publications

    Search author on:PubMed Google Scholar

  2. Jieqiu Chen
    View author publications

    Search author on:PubMed Google Scholar

Corresponding author

Correspondence to Jieqiu Chen.

Additional information

Both authors supported in part by NSF Grant CCF-0545514.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Burer, S., Chen, J. Relaxing the optimality conditions of box QP. Comput Optim Appl 48, 653–673 (2011). https://doi.org/10.1007/s10589-009-9273-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10589-009-9273-2

Keywords