Asymptotic behavior of a discrete-time density-dependent SI epidemic model with constant recruitment

Abstract

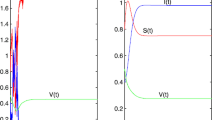
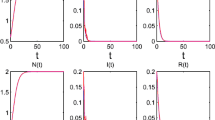
We use the epidemic threshold parameter, ${{\mathcal {R}}}_{0}$, and invariant rectangles to investigate the global asymptotic behavior of solutions of the density-dependent discrete-time SI epidemic model where the variables $S_{n}$ and $I_{n}$ represent the populations of susceptibles and infectives at time $n = 0,1,\ldots$, respectively. The model features constant survival “probabilities” of susceptible and infective individuals and the constant recruitment per the unit time interval $[n, n+1]$ into the susceptible class. We compute the basic reproductive number, ${{\mathcal {R}}}_{0}$, and use it to prove that independent of positive initial population sizes, ${{\mathcal {R}}}_{0}<1$ implies the unique disease-free equilibrium is globally stable and the infective population goes extinct. However, the unique endemic equilibrium is globally stable and the infective population persists whenever ${{\mathcal {R}}}_{0}>1$ and the constant survival probability of susceptible is either less than or equal than 1/3 or the constant recruitment is large enough.