Skip to main content

Advertisement

Springer Nature Link
Log in

An efficient numerical method for a singularly perturbed Fredholm integro-differential equation with integral boundary condition

  • Original Research
  • Published:
Journal of Applied Mathematics and Computing Aims and scope Submit manuscript

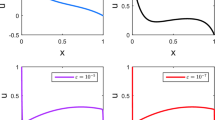
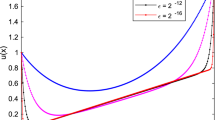
Abstract

In this paper, a linear singularly perturbed Fredholm integro-differential initial value problem with integral condition is being considered. On a Shishkin-type mesh, a fitted finite difference approach is applied using a composite trapezoidal rule in both; in the integral part of equation and in the initial condition. The proposed technique acquires a uniform second-order convergence in respect to perturbation parameter. Further provided the numerical results to support the theoretical estimates.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Abdulghani, M., Hamoud, A., Ghandle, K.: The effective modification of some analytical techniques for Fredholm integro-differential equations. Bulletin of the International Mathematical Virtual Institute 9, 345–353 (2019)

    MATH  Google Scholar 

  2. Abdullah, J.T.: Numerical solution for linear Fredholm integro-differential equation using Touchard polynomials. Baghdad Sci. J. 18(2), 330–337 (2021)

    Google Scholar 

  3. Amiraliyev, G.M., Durmaz, M.E., Kudu, M.: Uniform convergence results for singularly perturbed Fredholm integro-differential equation. J. Math. Anal. 9(6), 55–64 (2018)

    Google Scholar 

  4. Amiraliyev, G.M., Durmaz, M.E., Kudu, M.: Fitted second order numerical method for a singularly perturbed Fredholm integro-differential equation Bull. Belg. Math. Soc. - Simon Stevin 27(1), 71–88 (2020)

    MATH  Google Scholar 

  5. Amiraliyev, G.M., Durmaz, M.E., Kudu, M.: A numerical method for a second order singularly perturbed Fredholm integro-differential equation. Miskolc Math. Notes 22(1), 37–48 (2021)

    Article  MATH  Google Scholar 

  6. Amiraliyev, G.M., Mamedov, Y.D.: Difference schemes on the uniform mesh for singularly perturbed pseudo-parabolic equations. Turkish J. Math. 19, 207–222 (1995)

    MATH  Google Scholar 

  7. Arqub, O.A., Al-Smadi, M., Shawagfeh, N.: Solving Fredholm integro-differential equations using reproducing kernel Hilbert space method. Appl. Math. Comput. 219(17), 8938–8948 (2013)

    MATH  Google Scholar 

  8. Brunner, H.: Contemporary Computational Mathematics-A Celebration of the 80th Birthday of Ian Sloan. In: Dick, J., et al. (eds.) Numerical Analysis and Computational Solution of Integro-Differential Equations, pp. 205–231. Springer, Cham (2018)

    MATH  Google Scholar 

  9. Cakir, M.: A numerical study on the difference solution of singularly perturbed semilinear problem with integral boundary condition. Math. Model. Anal. 21(5), 644–658 (2016)

    Article  MATH  Google Scholar 

  10. Cakir, M., Arslan, D.: A new numerical approach for a singularly perturbed problem with two integral boundary conditions. Comput. Appl. Math. 40, 189 (2021)

    Article  MATH  Google Scholar 

  11. Cannon, J.R.: The solution of the heat equation subject to the specification of energy. Q. Appl. Math. 21(2), 155–160 (1963)

    Article  MATH  Google Scholar 

  12. Chen, J., He, M., Huang, Y.: A fast multiscale Galerkin method for solving second order linear Fredholm integro-differential equation with Dirichlet boundary conditions. J. Comput. Appl. Math. 364, 112352 (2020)

    Article  MATH  Google Scholar 

  13. Cimen, E., Cakir, M.: A uniform numerical method for solving singularly perturbed Fredholm integro-differential problem. Comput. Appl. Math. 40, 42 (2021)

    Article  MATH  Google Scholar 

  14. Dag, H.G., Bicer, K.E.: Boole collocation method based on residual correction for solving linear Fredholm integro-differential equation. Journal of Science and Arts 3(52), 597–610 (2020)

    Article  Google Scholar 

  15. Durmaz, M.E., Amiraliyev, G.M.: A robust numerical method for a singularly perturbed Fredholm integro-differential equation. Mediterr. J. Math. 18, 1–17 (2021)

    Article  MATH  Google Scholar 

  16. Durmaz, M.E., Amiraliyev, G.M., Kudu, M.: Numerical solution of a singularly perturbed Fredholm integro differential equation with Robin boundary condition. Turk. J. Math. 46(1), 207–224 (2022)

    MATH  Google Scholar 

  17. Dzhumabaev, D.S., Nazarova, K.Z., Uteshova, R.E.: A modification of the parameterization method for a linear boundary value problem for a Fredholm integro-differential equation. Lobachevskii J. Math. 41, 1791–1800 (2020)

    Article  MATH  Google Scholar 

  18. Farrell, P.A., Hegarty, A.F., Miller, J.J.H., O’Riordan, E., Shishkin, G.I.: Robust Computational Techniques for Boundary Layers. Chapman Hall/CRC, New York (2000)

    Book  MATH  Google Scholar 

  19. Hamoud, A.A., Ghadle, K.P.: Usage of the variational iteration technique for solving Fredholm integro-differential equations. J. Comput. Appl. Mech. 50(2), 303–307 (2019)

    Google Scholar 

  20. Hosseini, S.M., Shahmorad, S.: Tau numerical solution of Fredholm integro-differential equations with arbitrary polynomial bases. Appl. Math. Model. 27(2), 145–154 (2003)

    Article  MATH  Google Scholar 

  21. Ionkin, N.I.: Solution of a boundary value problem in heat conduction theory with nonlocal boundary conditions. Differ. Equ. 13, 294–304 (1977)

    Google Scholar 

  22. Kadalbajoo, M.K., Gupta, V.: A brief survey on numerical methods for solving singularly perturbed problems. Appl. Math. Comput. 217, 3641–3716 (2010)

    MATH  Google Scholar 

  23. Keimer, A., Pflug, L.: Modeling infectious diseases using integro-differential equations: Optimal control strategies for policy decisions and Applications in COVID-19, (2020), https://doi.org/10.13140/RG.2.2.10845.44000

  24. Kudu, M., Amirali, I., Amiraliyev, G.M.: A finite-difference method for a singularly perturbed delay integro-differential equation. J. Comput. Appl. Math. 308, 379–390 (2016)

    Article  MATH  Google Scholar 

  25. Kudu, M.: A parameter uniform difference scheme for the parameterized singularly perturbed problem with integral boundary condition, Adv. Differ. Equ., 170 (2018)

  26. Miller, J.J.H., O’Riordan, E., Shishkin, G.I.: Fitted Numerical Methods for Singular Perturbation Problems: Error Estimates in the Maximum Norm for Linear Problems in One and Two Dimensions, Rev World Scientific, Singapore (2012)

    Book  MATH  Google Scholar 

  27. Nayfeh, A.H.: Introduction to Perturbation Techniques. Wiley, New York (1993)

    MATH  Google Scholar 

  28. Nicoud, F., Schönfeld, T.: Integral boundary conditions for unsteady biomedical CFD applications. Int. J. Numer. Methods Fluids 40, 457–465 (2002)

    Article  MATH  Google Scholar 

  29. O’Malley, R.E.: Singular Perturbations Methods for Ordinary Differential Equations. Springer, New York (2013)

    Google Scholar 

  30. Panda, A., Mohapatra, J., Amirali, I.: A second-order post-processing technique for singularly perturbed Volterra integro-differential equations. Mediterr. J. Math. 18, 231 (2021)

    Article  MATH  Google Scholar 

  31. Panda, A., Mohapatra, J., Reddy, N.R.: A comparative study on the numerical solution for singularly perturbed Volterra integro-differential equations. Comput. Math. Model. 32, 364–375 (2021)

    Article  MATH  Google Scholar 

  32. Pour-Mahmoud, J., Rahimi-Ardabili, M.Y., Shahmorad, S.: Numerical solution of the system of Fredholm integro-differential equations by the Tau method. Appl. Math. Comput. 168(1), 465–478 (2005)

    MATH  Google Scholar 

  33. Roos, H.G., Stynes, M., Tobiska, L.: Robust Numerical Methods for Singularly Perturbed Differential Equations. Springer-Verlag, Berlin Heidelberg (2008)

    MATH  Google Scholar 

  34. Samarskii, A.A.: The Theory of Difference Schemes. Marcell Dekker, Inc., New York (2001)

    Book  MATH  Google Scholar 

  35. Shakti, D., Mohapatra, J.: A second order numerical method for a class of parameterized singular perturbation problems on adaptive grid. Nonlinear Eng. 6(3), 221–228 (2017)

    Article  Google Scholar 

  36. Shakti, D., Mohapatra, J.: A uniformly convergent numerical scheme for singularly perturbed differential equation with integral boundary condition arising in neural network. Int. J. Computing Science and Mathematics 10(4), 340–350 (2019)

    Article  MATH  Google Scholar 

  37. Tair, B., Guebbai, H., Segni, S., Ghiat, M.: An approximation solution of linear Fredholm integro-differential equation using Collocation and Kantorovich methods. J. Appl. Math, Comput (2021)

    MATH  Google Scholar 

  38. Tair, B., Guebbai, H., Segni, S., Ghiat, M.: Solving linear Fredholm integro-differential equation by Nyström method. J. Appl. Math. Comput. Mech. 20(3), 53–64 (2021)

    Article  MATH  Google Scholar 

  39. Thieme, H.R.: A model for the spatial spread of an epidemic. J. Math. Biol. 4, 337–351 (1977)

    Article  MATH  Google Scholar 

  40. Turkyilmazoglu, M.: Analytic approximate solutions of parameterized unperturbed and singularly perturbed boundary value problems. Appl. Math. Model. 35(8), 3879–3886 (2011)

    Article  MATH  Google Scholar 

  41. Turkyilmazoglu, M.: An effective approach for numerical solutions of high-order Fredholm integro-differential equations. Appl. Math. Comput. 227, 384–398 (2014)

    MATH  Google Scholar 

  42. Turkyilmazoglu, M.: High-order nonlinear Volterra - Fredholm - Hammerstein integro-differential equations and their effective computation. Appl. Math. Comput. 247, 410–416 (2014)

    MATH  Google Scholar 

  43. Turkyilmazoglu, M.: Effective computation of exact and analytic approximate solutions to singular nonlinear equations of Lane-Emden-Fowler type. Appl. Math. Model. 37, 7539–7548 (2013)

    Article  MATH  Google Scholar 

  44. Yalcinbas, S., Sezer, M., Sorkun, H.H.: Legendre polynomial solutions of high-order linear Fredholm integro-differential equations. Appl. Math. Comput. 210(2), 334–349 (2009)

  45. Yapman, Ö., Amiraliyev, G.M.: Convergence analysis of the homogeneous second order difference method for a singularly perturbed Volterra delay-integro-differential equation. Chaos Solit. Fractals 150, 111100 (2021)

    Article  MATH  Google Scholar 

Download references

Author information

Author notes

  1. Ilhame Amirali and Gabil M. Amiraliyev have contributed equally to this work.

Authors and Affiliations

  1. Department of Information Technology, Kırklareli University, Kırklareli, 39100, Turkey

    Muhammet Enes Durmaz

  2. Department of Mathematics, Faculty of Arts and Sciences, Düzce University, Düzce, 81620, Turkey

    Ilhame Amirali

  3. Department of Mathematics, Faculty of Arts and Sciences, Erzincan Binali Yıldırım University, Erzincan, 24100, Turkey

    Gabil M. Amiraliyev

Authors
  1. Muhammet Enes Durmaz
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Ilhame Amirali
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Gabil M. Amiraliyev
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Muhammet Enes Durmaz.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Durmaz, M.E., Amirali, I. & Amiraliyev, G.M. An efficient numerical method for a singularly perturbed Fredholm integro-differential equation with integral boundary condition. J. Appl. Math. Comput. 69, 505–528 (2023). https://doi.org/10.1007/s12190-022-01757-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12190-022-01757-4

Keywords