Introduction

In the realm of machine learning, the significance of large-scale datasets in the training of deep models cannot be overstated. However, the consolidation of data from disparate sources onto a centralized server for model training poses considerable challenges to data privacy. Addressing these concerns, Lin et al.  [1] introduced federated learning (FL), a novel privacy-preserving machine learning paradigm facilitating collaborative model training without necessitating the aggregation of raw data.

Fig. 1
figure 1

Illustrations of the differences between the existing federated learning methods for solving client-side noise and the proposed BCFFL method. The dots with dash line denote noisy data, and the red solid line denotes the classification boundary on local learning, and the gray dash line denotes the updated boundary after global learning. a Typical robust heterogeneous federated learning method, which adds an extra clean data set on the server side. b One-stage based HFL method, which implements clean data selection or noisy data elimination in one-stage manner based on specific assumption of clean data distribution. c Our proposed BCFFL method based on coarse-to-fine framework, which evenly build the client model from simple to difficult paradigm

Full size image

Presently, extant methodologies in federated learning [2, 3] are predicated upon the assumption of the veracity and cleanliness of client data. However, practical scenarios often witness disparate participating clients collecting data in a manner that deviates from independent and identically distributed (non-IID) conditions, thereby potentially harboring specific noise endemic to their local distributions. These perturbations significantly undermine the stability of both client and server models, inevitably compromising the efficacy of federated learning techniques [4]. To address the exigency for robust federated learning (RFL), contemporary approaches typically resort to server-side augmentation through the incorporation of supplementary clean datasets or pivot towards client-side interventions such as sample selection [5], sample reweighting [6], or label correction [7, 8]. Nonetheless, these strategies are invariably contingent upon a uniform client structure, a constraint often untenable in diverse practical contexts. In domains like healthcare, finance, and artificial intelligence services, customized requirements necessitate bespoke client structures. Thus, Li et al. [9] proffered a personalized heterogeneous federated learning (HFL) framework, depicted in Fig. 1, capable of accommodating distinct local architectures while harnessing knowledge exchange without compromising data privacy or divulging local model specifics. HFL empowers each client with a customized dataset and model design, leveraging the paradigm of knowledge distillation for information exchange. Prior to collaboration, clients utilize a shared public dataset as a guidance, and through the quantification of information distribution discrepancies, glean insights from peer clients cause data privacy infringement.

To the best of our knowledge, recent advancements in robust heterogeneous federated learning have introduced methods [5, 10, 11] that incorporate additional clean datasets into the server-side model, allowing each client to acquire knowledge by aligning their feedback on public, irrelevant data. Concurrently, client-side models typically employ a one-stage robust federated learning (RFL) strategy to mitigate the adverse effects of noisy data. These approaches can be broadly categorized into coarse-grained [5, 12] and fine-grained [7, 13] techniques, which include strategies such as detecting or relabeling heterogeneous noise data [14] through well-defined sample selection or label correction mechanisms. However, different neural architectures exhibit varying sensitivities to distinct noise types, complicating the personalization of noisy sample selection across diverse clients with a unified strategy. This challenge makes it difficult to determine whether high-loss samples are hard negative samples or noisy data, thereby hindering the achievement of significant performance improvements by diverse local models. To address the challenges posed by noisy heterogeneous client scenarios, we propose a coarse-to-fine two-stage strategy to adaptively learn from samples ranging from easy to hard. In the first stage, we focus on identifying the most confident samples for different clients instead of eliminating noisy data, thereby establishing a simple baseline for each client based on their private data. In the second stage, we leverage existing strategies to detect noisy data and construct robust client models. This approach facilitates a more effective handling of noise and enhances the overall performance of heterogeneous federated learning systems.

We present a novel balanced coarse-to-fine federated learning (BCFFL) algorithm, comprising two integral components: balanced progressive learning (BPL) and coarse-to-fine learning (CFL). Sample selection inherently introduces significant disparities in sample sizes across clients, thereby engendering training process inconsistencies. To rectify this issue, we devise a balanced progressive learning framework by integrating the concept of self-paced learning. The BPL framework standardizes the effective learning trajectories for each client model, ensuring equitable knowledge extraction from comparable data volumes. Additionally, BPL evaluates the data’s learning difficulty at each iteration, sequentially addressing and mastering progressively challenging complexities in an ordered fashion. In the initial stage of the two-phase coarse-to-fine learning process, we employ the ramp-up smooth loss coupled with BPL to selectively identify a limited quantity of high-confidence clean data for each client. These heterogeneous baselines capture fundamental feature information, facilitating subsequent refinement of the client model into a coarser representation. Subsequently, in the second stage, we integrate symmetric cross-entropy loss in [15] with BPL to mitigate overfitting to noisy data in client models. Addressing label noise, where ground truth may inaccurately reflect the true distribution, we adopt a combined approach of cross-entropy loss and inverse cross-entropy loss to comprehensively learn challenging classes and alleviate the risk of overfitting to noisy data.The primary contributions of this study include:

  • Existing methods on HFL scenerio often ignore the inconsistency in model heterogeneity, failing to balance sample selection across diverse clients. To address this, we proposed a balanced progressive learning framework for noisy heterogeneous clients. The BPL framework does not rely on any assumptions on the distribution of noise labels, it evenly selects a limited amount of simple data, constructing client models in a paradigm that progresses from simple to difficult.

  • A one-stage sample selection strategy for HFL struggles to identify whether high-loss samples are hard negative samples or noisy data across diverse clients. To address this, we propose a two-stage coarse-to-fine learning framework. Initially, it leverages ramp-up smooth loss to guide the client model from clean samples with confidence. Then, a joint optimization of symmetric cross-entropy loss with BPL fine-tunes the model, keeping it away from noise data and preventing overfitting.

  • The effectiveness of the proposed method is evaluated across diverse datasets on both heterogeneous and homogeneous models, encompassing various noise types and levels. The experimental results demonstrate significant superiority compared to several state-of-the-art methods.

Related work

Federated learning

Federated learning was first proposed by McMahan [16], it introduces a distributed machine learning framework wherein multiple client devices contribute to aggregate a unified model. This process develops models locally on various devices and aggregates information from these local models to construct a global one. Compared to traditional centralized machine learning, federated learning exhibits enhanced data protection performance, particularly in privacy-sensitive scenarios. Recently, the application of federated learning faces growing challenges, notably concerning heterogeneous FL and robust FL. While many existing methods concentrate on addressing noise issues within homogeneous client settings, there is a research gap in tackling the problem of noisy heterogeneous clients.

Fig. 2
figure 2

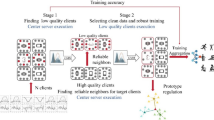
The diagram of our proposed BCFFL method for solving noisy heterogeneous clients. The different color dots denote clean data, and dots with solid line denote noisy data. The concept of balanced progressive learning (BPL) is intricately woven into the entire training process, selecting the similar limited size of simple samples to maintain the same convergence progress for heterogeneous clients. The proposed Coarse strategy firstly establishes the Fine-grained model as a coarse baseline with clean samples with high confidence, then refine this model into a fine-grained one, to alleviate overfitting of noise data

Full size image

Heterogeneous federated learning

Traditional federated learning requires uniform model structure across all local devices, and in the communication process, complete model parameters must be uploaded to the central server for aggregation. This leads to elevated communication costs and potential privacy risks. To overcome these limitations, researchers have shifted their focus to heterogeneous federated learning (HFL). Heterogeneous clients can be characterized by varying structures of deep models on different client devices. For instance, Diao et al. [17] proposed HeteroFL, a method that assigns domains of the global model to each heterogeneous device model, making each device responsible for updating a specific portion of the global model. HFL [18] takes it a step further by utilizing a parameter server to partition the domains that each device is responsible for, enabling uniform updates to global model parameters. HFL can aggregate convolutional blocks of different sizes and proposes FL tailored to distinct models. Yang et al. [19] and Collins et al.  [20] proposed methods similar to distillation learning, conducting FL on heterogeneous clients by preserving feature layers, such as specialized layers relevant to personalization. They aggregate only the layers preceding these specialized layers. Lin et al. [1] and Li et al. [9] introduced a knowledge distillation framework [21] to address this issue. However, these algorithms require additional datasets, contradicting the original parameter server setting that excludes any data. Moreover, their experiments overlook robustness of the clients, making the algorithm sensitive to noisy data.

Recently, Fang et al. [15] introduced an innovative approach wherein they design distinct network models for each local client. Leveraging public data, they adjusted model feedback to facilitate communication between heterogeneous clients. In the learning stage, the FL algorithm dynamically assigned weights to individual clients, aiming to alleviate noise arising from heterogeneous clients. However, a potential drawback exists: if certain client data exhibits distinctive characteristics or noise, the assigned higher weight to these samples may adversely affect other clients. Therefore, effective framework are imperative to mitigate the influence of noisy heterogeneous clients on federated learning during communication.

Federated learning with noisy labels

Many previous federated learning methods have overlooked the presence of noisy data, resulting in the deterioration of global model performance. Recently, robust federated learning(RFL) has emerged as a prominent topic. Approaches such as those presented in [22,23,24] utilize additional clean datasets and update sample weights based on gradient direction to mitigate the impact of noise in labels. Wang et al. [6] proposed the concept of adaptive learning rates and training intensity, while simultaneously selecting samples with high confidence [25] and discarding noisy samples. Self-paced methods as seen in [10, 26] and  [27], primarily incorporate regularization techniques to implement sample selection. Shi et al. [28] constructed a predefined course based on the small loss distances to select samples. In the training process, samples are gradually added to the course. However, this approach heavily relies on prior knowledge for selecting clean data, a factor that may vary across different deep networks.

Conversely, recent methods have shifted their focus to acquiring additional supervision from client model. Fedcorr et al. [7] introduced a multi-stage federated learning algorithm capable of detecting both noisy clients and noisy samples, followed by corrective actions. However, these corrections require high computational complexity and extensive hyperparameter tuning. Another approach as presented in [29], seeks to obtain global supervision by aggregating local class-wise feature centroids to form global class-wise feature centroids. Meanwhile, Yang et al. [29] generate pseudo-labels by exchanging class centroids between the server and clients and formulate losses based on similarity. Although these methods can identify noisy data with the aid of global supervision, they are predominantly suitable for homogeneous clients. In the case of noisy heterogeneous clients, these methods may struggle to eliminate noisy data due to variations in class centroids among heterogeneous clients.

Coarse-to-fine heterogeneous federated learning

In this paper, we proposed a novel approach called Balanced Coarse-to-Fine Federated Learning(BCFFL) algorithm designed for addressing the internal noise in noisy heterogeneous clients.The algorithm workflow is shown in Fig. 2. The BCFFL framework is built upon the principles of Balanced Progressive Learning(BPL), which ensures that each client symmetrically extracts knowledge from a similar quantity of privacy data. Throughout the entire training stage, BPL sorts sample complexity from simple to difficult, maintaining similar convergence progress for heterogeneous clients. Based on BPL, the BCFFL algorithm comprises Coarse-to-Fine (CF) two stages: in the first stage, we employ a ramp-up smooth loss to selectively identify clean data with high confidence, establishing a coarse baseline for each client. At second stage, we introduce symmetric cross-entropy loss to refine the coarse baseline into a fine-grained one. The joint optimization of cross-entropy loss and the inverse cross-entropy loss facilitates comprehensive learning of challenging samples, thereby preventing overfitting of noise data. This coarse-to-fine framework effectively address the issue of internal label noise in heterogeneous client devices, resulting in a more accurate and robust model for each client.

Problem Formulation and Terminology

Here, we define federated learning scenario with a multi-class classification task, involving C clients and one server. \(\textrm{C}\) is the set of all clients, and the \(\textrm{k}\)-th client \(c_{k}\in \textrm{C}\) possesses a private dataset \({\varvec{D}_{k}=\{{(\varvec{x}_{i}^{(k)},{\textbf {y}}_{i}^{(k)})} \}_{i=1}^{^{N_{k}}}}\), where \(N_{k}\) is the sample size for client \(c_{k}\), and \({\varvec{x}}_{i}^{(k)}\) denotes the i-th sample in \({\varvec{D}_{k}}\), and \(\varvec{y}_{i}^{(k)} \in \left\{ 0,1 \right\} \) represents a one-hot vector of the ground truth labels, respectively. Additionally, each client \(c_{k}\) holds a set of parameters \(\varvec{\Theta }_{k}\) for local model \(f_k(\cdot )\) with a distinct model design. \(\hat{\varvec{y}}_{i}^{(k)}=f_k(\varvec{x}_{i}^{(k)},\varvec{\Theta }_{k})\) denotes the output logits.

To update the local model parameters, the cross-entropy loss function is minimized for each client \(c_k\):

$$\begin{aligned} L_{ce}=- {\sum _{i=1}^{N_k}} \, p(\varvec{x}_{i}^{(k)})\,{ log}\, (q\,(\varvec{x}_{i}^{(k)})) \end{aligned}$$
(1)

Here, \(\varvec{y}_{i}^{(k)}=p(\varvec{x}_{i}^{(k)})\) represents the true probability distribution of the ground truth, and \(\hat{\varvec{y}}_{i}^{(k)}=q(\varvec{x}_{i}^{(k)})\) represents the predicted logits.

Robust heterogeneous federated learning

In heterogeneous federated learning, the server lacks access to clients’ data and instead maintains a public dataset denoted as \({\varvec{D}_{0}}=\{{\varvec{x}_{i}^{(0)}} \}_{i=1}^{^{N_{0}}}\), which may belong to different classification tasks. For training HFL models, the learning process can be divided into global learning phase and local learning phase. For global learning, we use the public data serves as a bridge for facilitating collaborative learning among heterogeneous clients. Each client \(c_k\) uses the local model \(f_k(\cdot )\) to calculate logits on \({\varvec{D}_{0}}\). Subsequently, the client employs Kullback–Leibler (KL) divergence to quantify the difference in knowledge acquired from other clients. For local learning, the learning process follows the typical FL training strategy.

In this paper, our objective is to achieve robust heterogeneous federated learning in the presence of noisy data, so we suppose that each client has a private noisy dataset defined as \(\tilde{\varvec{D}}_{k}=\{{(\varvec{x}_{(i)}^{(k)},\tilde{\varvec{y}}_{j}^{(k)})}\}_{i=1}^{^{N_{k}}}\), where \(\tilde{\varvec{y}}_{i}^{(k)}\) represents the noisy labels for sample \({\textbf {x}}_{i}^{(k)}\). For ideal knowledge communications between HFL client models, we assume that the output of public data on each client model can be formulated as \(f(\varvec{x}_{i},\varvec{\Theta }_{k_1})=f(\varvec{x}_{i},\varvec{\Theta }_{k_2})\). Due to the heterogeneity of the models and the presence of different noisy patterns, the decision boundaries of each client is inconsistent. This implies that the noise data will have an impact on both the local learning and global leaning phases. The previously stated assumption may not be valid, and \(f(\varvec{x}_{i},\varvec{\Theta }_{k_1}) \ne f(\varvec{x}_{i},\varvec{\Theta }_{k_2})\). Therefore, the client \(c_k\) should pay attention to the impact of both internal noise and the noise of other clients.

Balanced progressive learning mechanism

In the balanced progressive learning(BPL), we leverage the self-paced learning(SPL) to achieve balanced sample selection for each iteration. This compels each client to symmetrically extract the same amount of knowledge from a comparable volume of privacy data. Self-paced learning, a variant of curriculum learning (CL) [26], is a training strategy inspired by human and animal learning processes. It gradually proceeds from easy to difficult samples, dynamically adjusting the curriculum based on the current model’s ability [27]. For given training dataset \(\tilde{\varvec{D}}_{k}\), Self-paced learning solves the following problem by selecting easy samples to learn the model parameters in each iteration. It uses a binary variable \({v}_i\) to control which samples are considered easy, and then updates the model by selecting a balanced quantity of these samples for each client. The BPL can be formulated as:

$$\begin{aligned} \begin{aligned}&\min _{{\varvec{\Theta }_{k}, \varvec{v}}}E\,({\varvec{\Theta }_{k}, \varvec{v}},\lambda \,) = { \sum _{i=1}^{N_k}}\,{ {v}}_{i}\, L\,(\,\varvec{y}_{i}^{(k)}, f\,(\varvec{x}_{i}^{(k)},\varvec{\Theta }_k\,))-\lambda {\sum _{i=1}^{N_k}{{v}}_{i}\,,} \\&\quad \text {s.t.}\,{\varvec{v}}\in \bigl \{ 0,1 \bigr \} \end{aligned}\nonumber \\ \end{aligned}$$
(2)

Here, the \(L\,(\,\varvec{y}_{i}^{(k)},f\,(\varvec{x}_{i}^{(k)},\varvec{\Theta }_k\,))\) denotes arbitrary loss between the ground truth and the prediction, and \(\lambda \) is the parameter that controls the learning pace. Equation 2 is usually solved using Divide-and-Conquer strategy  [30, 31] with an Expectation-Maximization(EM) optimization solver: first by fixing \(\varvec{\Theta }_k\), calculating \(\varvec{v}\), and then, with \(\varvec{v}\) fixed, updating the model parameters \(\varvec{\Theta }_k\) using the selected easy samples. The \(\varvec{v}\) optimization can be formulated as:

$$\begin{aligned} {{v}_i}=\left\{ \begin{array}{rcl} 1 & & L\;(\varvec{x}_{i}^{(k)},f\,(\varvec{x}_{i}^{(k)},\varvec{\Theta }_k))<\lambda ,\\ \\ 0 & & {otherwise.} \end{array} \right. \end{aligned}$$
(3)

The heterogeneous clients exhibit varying sensitivity to the presence of different noisy patterns. Relying solely on the effect of the neural network to select clean samples with high confidence from noisy data becomes challenging. This difficulty may result in the lack of synchronization in the convergence of each client, which make the HFL baised. Here, we employ SPL as a balanced progressive learning framework to homeostatically train heterogeneous clients. The BPL evaluates the learning difficulty of samples in each iteration and sorts the difficulty from easy to hard, then updates every client with supervision by selecting a balanced quantity of these samples for each client, where the sample selection is controlled by binary variable \(\varvec{v}\), which seeks to accurately learn the model by using a set of "easy" samples rather than using all the training data. When \(\lambda \) is small, only samples with low prediction loss are chosen as training sample. Conversely, when \(\lambda \) is large enough, all the samples are selected. Therefore, \(\lambda \) ensures that a comparable quantity of data is selected for each client, without impacting the convergence of the client model.

$$\begin{aligned} \varvec{v} \leftarrow {sort} \, (\,L \,(\varvec{y}_{i}^{(k)},\,f\,(\varvec{x}_{i}^{(k)},\varvec{\Theta }_k))) \end{aligned}$$
(4)

Here, we should mention that if we only update the model parameters using Eq. (4) throughout the learning stage, it can lead to a gradual degradation in model performance. This is because the heterogeneous clients may underfit with limited selected samples without training on hard-negative samples [14]. Hence, we propose a coarse-to-fine strategy with BPL to make the clients more stable.

Coarse learning stage

In the Coarse Learning Stage (CLS) with \(T_1\) epoch, we utilize a smoothing ramp-up curve as an adaptive scaling factor, represented by \(\gamma (t)\), to selectively identify clean data with high confidence based on BPL framework. This process establishes a coarse baseline for each client, enabling heterogeneous clients to better capture pertinent features for tasks. The function \(\gamma (t)\) is a time-dependent weighting function that calculates a weight value between 0 and 1 based on the current epoch.

$$\begin{aligned} \gamma \,(t)=\tau \, \textrm{e} ^{-5\,\left\| 1-\frac{t}{C} \right\| ^{2}} , t\le {T_{1}} \end{aligned}$$
(5)

Where \(\tau \) is the smoothing factor and C is a constant value. By multiplying this function with the cross-entropy loss, the weights of the noisy data samples are controlled. The weighted CE loss function for coarse learning stage at epoch t can be formulated as:

$$\begin{aligned} L_{wce}= -\frac{\gamma {(t)}}{N}{\sum _{i=1}^{N_k}} {v}_{i} p(\varvec{x}_{i}^{(k)})\,log(q(\varvec{x}_{i}^{(k)})) -\lambda {\sum _{i=1}^{N_k}{v}_{i}} \end{aligned}$$
(6)

Initially, the cross-entropy loss is multiplied by a smaller factor of the smooth function output. According to Eq. (3) of BPL, this deliberate manipulation maintains a low weight for noisy sample, resulting in the loss being lower than \(\lambda \), thereby forcing BPL to choose all samples in the first few epochs. As the training progresses, the weight of the noisy data gradually increases, achieved by multiplying a larger factor output of the smoothing function. Consequently, the loss value of noisy data will become larger than \(\lambda \), and BPL will adapt to selecting samples with high confidence. In the coarse progress phase, we sort loss function Eq. (6) with ramp-up smooth loss and set \(\lambda \) correspond to the loss value at a fixed percentage of the sample quantity.

Fine-grained learning stage

In robust heterogeneous federated learning, our objective is to mitigate the adverse effects of noise originating from internal clients. However, the coarse learning stage may cause some easy-to-learn classes to converge faster than others. To achieve full convergence of the difficult-to-learn classes, additional rounds of learning are required. In the second stage with \(T-T_1\) epoch, we aim to refine the coarse baseline model, placing emphasis on fully learning the difficult-to-learn classes while mitigating the risk of overfitting noisy labels by eliminating the noise data. To address the noise elimination on each client, we maintain the utilization of Symmetric Cross-Entropy Learning proposed in [15] throughout the fine-grained learning stage. In the presence of noisy labels, predictions may be more reliable than the given label. Therefore, in comparison to Eq. (1), p might not accurately represent the ground truth, conversely, q better reflects the true class distribution. The reverse cross-entropy (RCE) loss function [32] will handle this scenario, it can be expressed as:

$$\begin{aligned} L_{rce}=- {\sum _{i=1}^{N_k}}\,q\,(\varvec{x}_{i}^{(k)})\,{log}\,(p\,(\varvec{x}_{i}^{(k)})) \end{aligned}$$
(7)

By merging the CE loss with RCE loss, the Symmetric Cross-Entropy loss with balanced progressive learning for fine-grained stage can be formulated as:

$$\begin{aligned} L_{sce}&=- \alpha {\sum _{i=1}^{N_k}} {v}_{i} \,p\,(\varvec{x}_{i}^{(k)})\,{log}\,(q\,(\varvec{x}_{i}^{(k)}))\nonumber \\&\quad -{\sum _{i=1}^{N_k}} {v}_{i} \,q\,(\varvec{x}_{i}^{(k)})\,{log}\,(p\,(\varvec{x}_{i}^{(k)})) -\lambda {\sum _{i=1}^{N_k}{v}_{i}} \end{aligned}$$
(8)

Here, the hyperparameter \(\alpha \) serves as a constraint on the overfitting of SCEL to noise, optimized with gird search or particle swarm optimization [33]. The BPL eliminates the outliers with extremely large losses by self-paced learning. The CE loss enhances to the model’s fitting effectiveness for each class, while the RCE loss introduces the robustness against label noise. This combination prevents the negative impact of noisy or mislabeled data, leading to more stable and accurate model performance.

BCFFL training pipeline

In this paper, we proposed a novel Balanced Coarse-to-Fine Federated Learning(BCFFL) framework for solving the noisy heterogeneous clients. Our two-stage training strategy leverages a ramp-up smooth factor in the coarse stage to comprehensively learn the feature representations from simple samples. Subsequently, in the second stage, we incorporate symmetric cross-entropy loss to mitigate the impact of erroneous data, facilitating the generation of fine-grained and robust representations for the training data. Throughout the training process, we also present a balanced progressive learning framework that utilizes self-step learning to standardize the learning direction. This ensures that the model updates in the direction of a clean and efficient client. Here, we present the detailed procedure for local learning in Algorithm 1, we utilize the alternative convex search to get the local optima for each client, and the global learning process keeps the same as RHFL.

Algorithm 1
figure a

The training process of the proposed BCFFL Algorithm

Full size image

Experiments

Experimental setting

Datasets and models

In our experiments, threee datasets were involved: Cifar10, Cifar100  [34] and COVID-19 [35]. The Cifar10 dataset contains 60,000 32 \(\times \) 32 color images divided into 10 classes, with 6,000 images per class, while the Cifar100 dataset contains 60,000 32 \(\times \) 32 color images divided into 100 classes, with 600 images per class. We follow the same experiment settings as RHFL [15]. A subset with 5000 images of Cifar100 was used as a public dataset for global training and 1000 for testing, while 10,000 images randomly sampled from Cifar10 was denoted as private datasets for four clients. Meanwhile, we utilize the COVID-19 to evaluate the generalization of our model. The COVID-19 dataset comprises 21,165 images categorized into four classes, and we divided it into two parts: 90% was randomly sampled and evenly divided to serve as private datasets for each client, while the remaining portion was designated as a public dataset for the server. In the context of heterogeneous federated learning, our experiments began with the selection of four distinct networks: ResNet10 [36], ResNet12 [36], ShuffleNet [22], and MobileNetv2 [37] each functioning as an independent client. In the homogeneous model scenario, the networks of all four clients are set to the ResNet12 framework. This experimental setting aims to evaluate the robustness and accuracy of our method under both heterogeneous and homogeneous scenarios with noisy client data.

Table 1 The accuracy of the heterogeneous clients ResNet10, ResNet12, ShuffleNet and MobileNetv2 under Pairflip and Symflip noise scenarios when the noise rate was \(\mu =0.1\)
Full size table

Noisy label generation

In our proposed method, we add a label transition matrix to the private dataset for each client, and flip the correct label y to the noisy label \(\tilde{{\textbf {y}}}\) through the matrix Q. This procedure can be denoted as \(\mathrm{{\textbf {Q}}}_{mn}=flip(\tilde{y}=m,y=n)\), where m and n represent the original label and the flipped label, respectively. Here, matrix Q has two typical structures: symmetric flip [38] and pairwise flip [14]. Symmetric flip means that it randomly flips the original class label to any wrong class label with the same probability, and pairwise flip means that it only flips the original class label to a very similar wrong class label.

Implementation details

We built up the federated learning scenarios with four clients, and one server in our experiments. The server is unable to obtain the private datasets in the clients and has a common dataset \(\varvec{D}_{0}\) with 5000 samples. Each client has a private dataset with 1000 noise samples denoted as \(\tilde{\varvec{D}}_{k}\). We implement coarse-to-fine federated learning algorithm with PyTorch framework, and utilize the ResNet10, ResNet12, ShuffleNet and MobileNetv2 as backbone networks for four clients. The entire training process runs for \(T=80\) epochs.

To fairly evaluate the heterogeneous environment, we utilize the common dataset \(\varvec{D}_{0}\) serving as a linkage between clients for communication. During the global learning phase, each client \(c_{k}\) uses its local model \(f_k(\varvec{D}_{0}, \varvec{\Theta }_k)\) to evaluate the predictions on \(\varvec{D}_{0}\). In this manner, we update the model parameters \(\varvec{\Theta }_k\) for client \(C_{k}\). Clients utilize KL divergence to quantify dissimilarities in knowledge distribution with other clients, which can better balance local knowledge learning and knowledge from other clients. Additionally, for local learning phase, we set the Adam [19] optimizer with an initial learning rate \(\alpha =0.001\), and batch size 256, \(\lambda \) set as 0.1. For synthetic noise data, we set the noise rates to \(\mu \)=0.1 or 0.2 with two noisy types: symmetric flip and pairwise flip. To generate the noisy dataset \(\tilde{D} \), we flip \(20\%\) of the labels to incorrect labels in the training dataset of Cifar10 [34] and keep the test dataset of Cifar10 unchanged to evaluate the model’s performance.

Comparison with the state-of-the-art methods

In heterogeneous federated learning scenario, we evaluate the superiority of our method under different noise-rate and noise-type scenarios. The proposed method is compared with the state-of-the-art methods across various noise rates and noise types. We conducted multiple sets of contrasting experiments, incorporating noise-free techniques like FedMD [9], FedDF [1], RHFL [15] and AugHFL [39], along with heterogeneous FL algorithms such as FedAvg [16] and FCCL [40]. FCCL addresses heterogeneity by combining interrelation matrix construction with knowledge distillation. For robust learning, FedMD and FedDF developed a distillation framework that enables the integration of diverse models and data in a robust federated learning setting. RHFL solves the robustness of noisy heterogeneous clients through feedback on client data knowledge distribution and flexible sample-weighted method. By contrast, AugHFL enhances the robustness of heterogeneous clients through data augmentation and a re-weighted communication.

Heterogeneous federated learning methods

Here, we evaluate the performance with noise rate \(\mu = 0.1\) and \(\mu = 0.2\). The Tables 1 show that our method achieves best accuracy across various noise rates on CIFAR dataset. As the noise rate rises from \(\mu =0.1\) to \(\mu =0.2\), the average accuracy of noise-sensitive methods drops significantly, by 4.19% for HFL and 1.37% for FCCL on pairflip noise. The experimental results demonstrate that robust federated learning methods is superior than noise-sensitive methods, while they are not fit for the heterogeneous federated learning scenarios. As for FedMD [9] and FedDF [1], it drops 5.02% and 5.85% on pairflip noise, 4.52% and 4.69% on symflip noise. By contrast, robust heterogeneous federated learning methods, RHFL, AugHFL and our BCFFL perform well than other comparable methods. The average accuracy improves from 74.76% to 77.34% than HFL. Compared with one-stage based RHFL, our two-stage BCFFL method improve the average accuracy by 2.58% on \(\mu =0.1\) and 1.41% on \(\mu =0.2\), the experiments shows that two-stage coarse-to-fine strategy forces the sample selection from samples with high confidence to low confidence. These strategy avoid the instability caused by incorrect labels, allowing the model to converge faster with the same training iterations. Meanwhile, the variance of the accuracy on four heterogeneous clients on proposed BCFFL is 8.59, which is much lower than its 17.01 of RHFL. This results conclude that our proposed balanced learning framework achieving substantial and stable performance improvements by symmetrically extracting the knowledge from the comparable quantity of data for each client. For different noise type, the noise-sensitive method decrease 1.11% from pairflip to symflip noise, while our proposed method shows the stable performance under diverse noise types and noise rates, by 77.34% to 77.80% on \(\mu \) = 0.1.

Table 2 Compared with state-of-the-art methods in similar model settings, we set all four local models to ResNet12 and demonstrate using the average test accuracy of the local model
Full size table

Homogeneous federated learning methods

In this experiment, we aim to evaluate the generality of our proposed method, and test the performance under the homogeneous scenario. In Table 2, the experimental results show that our method achieves the best performance compared with the state-of-the-art robust federated learning methods in a homogeneous model setting. The experimental results also indicate a significant 12.76% improvement over the baseline, when the noise type is set to symmetric flipping noise with 20% noise rate. In this scenario, the average test accuracy of our method reached 79.63%, surpassing the performance of the current existing algorithm RHFL [15], which only achieved an accuracy of 78.83%.

Table 3 Ablation experiments
Full size table

Ablation study

Component analysis

In this paper, we proposed a balanced coarse-to-fine framework to address the noisy heterogeneous federated learning. The proposed BCFFL algorithm comprises two integral components: the balanced progressive learning (BPL) framework and coarse-to-fine learning framework. The latter, in turn, is structured into two stages: coarse learning stage (CLS) and fine-grained learning stage (FGLS). We empirically evaluate the efficacy of each component independently. In our experiment, we set the noise rate to 0.1, with pairflip and symflip noises as the noise type. Theoretically, our method degrades to the baseline HFL without the key components (BPL & CLS & FGLS), and to be RHFL only with FGLS component. The experiment results depicted in Table 3 show that only FGLS component added to RHFL prevents the client model from overfitting on noisy data, resulting in a 0.77% improvement in average accuracy. The CLS component, which selects the samples with high confidence, achieves stable performance with an average accuracy of 75.90%, surpassing the baseline by 1.91% and RHFL by 1.14%. However, it is challenging to discern whether high-loss samples are hard negatives or noisy data, limiting the improvement from noise elimination. Integrating both FGLS and CLS outperforms each single stage, demonstrating that the effectiveness of the two-stage learning strategy, resulting in a 1.24% improvement. Moreover, combination BPL with either FGLS or CLS or both components leads to additional improvements in average accuracy, by 0.36%, 0.36% and 0.88% on symflip noise, respectively. This consistency highlights the role of BPL in evenly selecting a limited amount of simple data throughout the training phase. In conclusion, the joint framework achieves optimal performance in noisy HFL scenarios, showcasing the effectiveness of the proposed method.

Fig. 3
figure 3

The impact of smoothing factor and the weight of cross-entropy loss on heterogeneous clients under Pairflip and Symflip noise types when the noise rate was \(\mu =0.1\). a and b show the impact of the smoothing factor on accuracy under Pairflip and Symflip noise types, respectively, when the noise rate was \(\mu =0.1\). c and d show the impact of the weight of the cross-entropy loss on accuracy under Pairflip and Symflip noise types respectively when the noise rate was \(\mu =0.1\)

Full size image
Table 4 The accuracy of the heterogeneous clients with InceptionV3, ResNet18, ResNet34 and VGG16 under Pairflip and Symflip noise scenarios when the noise rate was \(\mu =0.1\)
Full size table

Hyperparameter sensitivity

To perform a comprehensive sensitivity analysis for the hyperparameters in our BCFFL, we conducted a series of experiments on the CIFAR-10 dataset using two distinct noise types with noise rate \(\mu =0.1\). Our objective was to evaluate the impact of two hyperparameters the smoothing factor T in Eq. (5) and the weight \(\alpha \) of loss function in Eq. (8), respectively. The experimental results depicted in Fig. 3 illustrate the best performance is achieved when the smoothing factor is set to 10 and the weight of cross-entropy is set to 0.1. We found that \(\tau \) was not significantly sensitive to different noise types, while increasing the value of \(\alpha \) to 1.0 led to a decline in performance. This suggests that a higher weight of reverse CE loss can result in eliminating the noisy data to achieve high-quality training performance.

Generalization evaluation

To perform evaluation on generalization, we conducted experiments on additional COVID-19 dataset to test on those real-world FL scenarios. The experimental results in Table 1 demonstrate that our BCFFL outperforms other robust FL approaches, resulting in 0.99%, 0.50%, 1.67% and 1.76% improvement in average accuracy on four noisy heterogeneous scenarios. This suggests our method perform significantly well on more complex data distributions. Meanwhile, we replaced the client models from ResNet10, ResNet12, ShuffleNet, and MobileNetv2 with other four neural architectures: InceptionV3 [41], ResNet18, ResNet34, and VGG16 [42]. The experimental results presented in Table 4 demonstrate that, even after changing the models, our performance remains the best compared to other methods with 0.85% improvement in average accuracy.

Conclusion

In this paper, we propose a two-stage coarse-to-fine federated learning framework for noisy heterogeneous clients. The framework incorporates a balanced progressive learning (BPL) strategy, inspired by self-paced learning, to facilitate the construction of client models from simple to difficult manner. In the coarse stage, the method utilizes a ramp-up smooth loss with BPL, enabling the client model to confidently learn features from clean samples with high confidence. In the fine-grained stage, we jointly optimize the symmetric cross-entropy, which help the client model avoid noise data. Experimental results demonstrate that our method outperforms state-of-the-art methods, exhibiting superior performance across two popular benchmarks and various noisy heterogeneous scenarios. In the future, we plan to focus on mitigating model performance degradation caused by multiple corruptions in heterogeneous federated learning.