Hostname: page-component-55f67697df-bzg56 Total loading time: 0 Render date: 2025-05-09T15:30:32.466Z Has data issue: false hasContentIssue false
  • English
  • Français

Compact serialization of Prolog terms (with catalan skeletons, cantor tupling and Gödel numberings)

Published online by Cambridge University Press:  25 September 2013

PAUL TARAU
PAUL TARAU*
Affiliation:
Department of Computer Science and Engineering (e-mail: tarau@cs.unt.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

We describe a compact serialization algorithm mapping Prolog terms to natural numbers of bit-sizes proportional to the memory representation of the terms. The algorithm is a ‘no bit lost’ bijection, as it associates to each Prolog term a unique natural number and each natural number corresponds to a unique syntactically well-formed term.

To avoid an exponential explosion resulting from bijections mapping term trees to natural numbers, we separate the symbol content and the syntactic skeleton of a term that we serialize compactly using a ranking algorithm for Catalan families.

A novel algorithm for the generalized Cantor bijection between 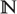${\mathbb{N}$ and 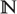${\mathbb{N}$k is used in the process of assigning polynomially bounded Gödel numberings to various data objects involved in the translation.

Keywords

bijective serialization of Prolog termsranking/unranking of Catalan familiesgeneralized Cantor n-tupling bijectioncombinatorial number system
Type
Regular Papers
Information
Theory and Practice of Logic Programming , Volume 13 , Special Issue 4-5: 29th International Conference on Logic Programming , July 2013 , pp. 847 - 861
Copyright
Copyright © 2013 [PAUL TARAU] 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Buckles, B. P. and Lybanon, M. 1977. Generation of a vector form the lexicagraphical index [G6]. ACM Transactions on Mathematical Software 5, 2 (June), 180–182.CrossRefGoogle Scholar
Cegielski, P. and Richard, D. 1999. On arithmetical first-order theories allowing encoding and decoding of lists. Theoretical Computer Science 222, 12, 55 – 75.CrossRefGoogle Scholar
Gödel, K. 1931. Über formal unentscheidbare Sätze der principia mathematica und verwandter systeme I. Monatshefte für Mathematik und Physik 38, 173–198.CrossRefGoogle Scholar
Hartmanis, J. and Baker, T. P. 1974. On simple goedel numberings and translations.. In ICALP (2002-02-01), Loeckx, J., Ed. Lecture Notes in Computer Science, vol. 14, Springer, Berlin Heidelberg, 301–316.Google Scholar
Knuth, D. E. 2005. The Art of Computer Programming, Volume 4, Fascicle 3: Generating All Combinations and Partitions. Addison-Wesley Professional.Google Scholar
Knuth, D. E. 2006. The Art of Computer Programming, Volume 4, Fascicle 4: Generating All Trees–History of Combinatorial Generation (Art of Computer Programming). Addison-Wesley Professional.Google Scholar
Kreher, D. L. and Stinson, D. 1999. Combinatorial Algorithms: Generation, Enumeration, and Search. The CRC Press Series on Discrete Mathematics and its Applications, CRC Press, Inc.Google Scholar
Lehmer, D. H. 1964. The machine tools of combinatorics. In Applied Combinatorial Mathematics, Wiley, New York, 5–30.Google Scholar
Liebehenschel, J. 2000. Ranking and unranking of a generalized Dyck language and the application to the generation of random trees. Séminaire Lotharingien de Combinatoire 43, 19.Google Scholar
Lisi, M. 2007. Some remarks on the Cantor pairing function. Le Matematiche 62, 1.Google Scholar
Martinez, C. and Molinero, X. 2003. Generic algorithms for the generation of combinatorial objects. In MFCS, Rovan, B. and Vojtas, P., Eds. Lecture Notes in Computer Science, vol. 2747, Springer, Berlin Heidelberg, 572–581.Google Scholar
Salomaa, A. 1973. Formal Languages. Academic Press, New York.Google Scholar
Tarau, P. 2009. An embedded declarative data transformation language. In Proceedings of 11th International ACM SIGPLAN Symposium PPDP 2009, ACM, Coimbra, Portugal, 171–182.Google Scholar
Tarau, P. 2011. Bijective term encodings. In CICLOPS'2011, Lexington, KY.Google Scholar
Tarau, P. 2012. Deriving a fast inverse of the generalized cantor N-tupling bijection. In 28th International Conference on Logic Programming - Technical Communications (ICLP'12), Dovier, A. and Costa, V. S., Eds. Budapest, Hungary.Google Scholar
Supplementary material: PDF

Tarau supplementary material

Appendix

Download Tarau supplementary material(PDF)
PDF 128.1 KB