Introduction

High accuracy and high resolution are urgently required in high pressure measurements in variety fields, such as ocean science, petroleum industry, downhole drilling and gas transportation, and microelectro-mechanical system (MEMS) pressure sensors have the potential to be widely applied in these fields1,2,3,4,5. In the current studies, piezoresistive and capacitive microsensors, which take advantages of simple structure and low cost, have been applied in a wide range pressure measurement by modifying the size or shape of the diaphragm or the cavity. However, these high-pressure microsensors are all suffer from low accuracies in full-range of pressure and temperature6,7,8,9. Alternatively, resonant pressure microsensors offer the benefits of high accuracy and outstanding resolution, opening up new possibilities for high-pressure measurement. Kinnell suggested that these microsensors, which rely on a pressure-sensitive diaphragm, have the potential to measure a wide range of pressures, up to 70 MPa10.

Several resonant high-pressure microsensors based on diaphragm deformation were developed in previous works11,12,13. To enhance the durability of the diaphragm across a wide pressure range, its stiffness was augmented by making it smaller and thicker, which brought out the problem of unmatched of pressure sensitivity of two resonators, leading a poor differential effect14. Though there are also methods to modify the shape of the pressure sensitive diaphragm, the measurement range is limited to 30 MPa because of the stress concentration caused by the diaphragm15. Compared to diaphragm sensing, the volume compressed sensing is a new way for pressure sensing without stress concentration, indicating a theoretically much higher strength. It has been firstly applied in piezoresistive high pressure microsensors in 2009 with poor accuracy of 0.3% from 0 to 100 MPa16. Continuous research was conducted and improved the measurement accuracy by optimizing the structure17,18,19,20,21. Due to the buckling of a clamp-clamp resonator anchored inside a microsensor based on volume compressed sensing while high pressure applied, this principle of pressure sensing has not been applied in resonant high-pressure sensors until Yokogawa Inc. proposed a microsensor for high-pressure measurement in 2016 with a complex fabrication process22,23, introducing tensile pre-stress through doping to protect resonators from buckling, achieving high-pressure measurement. A further report in 2023 indicated that this microsensor has high stability and resolution24; In 2023, the Aerospace Information Research Institute developed a novel resonant pressure microsensor based on volume compressed sensing with Y-shaped micro-beam anchors to avoid the buckling of resonators under high pressure, but only a qualitative mechanism of the micro beams was obtained25. At the same time, the Au/Si eutectic bonding was adopted for vacuum packaged. However, external temperature sensors were still needed for temperature compensation, and measurements were only conducted within the range of 7 MPa; Later, a pressure microsensor based on a composite pressure-sensitive mechanism was developed, which combined diaphragm bending and volume compression to realize pressure/stress transitions. However, its size increased with the introduction of the diaphragm26.

In order to further explore the principle of volume compressed, this paper firstly introduced a theoretical model for micro beams and obtained an expression for the influence of micro beam structure on pressure sensitivity. Combined the theoretical analysis and the fabrication methods, a resonant high-pressure microsensor with dual resonators based on volume compressed sensing was developed. Both resonators were supported by micro-beam anchors in different structural design, leading to varying pressure sensitivities, which can be utilized for temperature compensation. Dealing with potentially complex hydraulic measurement, the microsensors fixed on an isolation structure were surrounded by silicone oil together, and sealed with a corrugated diaphragm and a base. Compared to previous work, this microsensors performed a temperature self-compensation by dual resonators with different pressure sensitivities, and a high accuracy can be featured within 0.1~70 MPa from −10 °C to 50 °C. The resolution and response time are also characterized, indicating that the high-pressure sensor can meet practical application requirements

Design and simulation

Structural design and sensing principle

Figure 1a shows the overall structural design of the microsensor, which mainly consists of two parts: a SOI wafer and a silicon wafer as cap. Micro-beam supports and resonators are placed on the device layer in SOI. In details, there are Resonant I, which is insensitive to pressure for temperature compensation, Resonator II, which is sensitive to pressure, as well as micro-beam supports and driving and detection electrodes. The resonators are connected to the anchors through micro-beam supports as shown in Fig. 1b. The silicon cap and device layer of the SOI are bonded by Au/Si eutectic bonding, implementing vacuum packaged for the resonators. Silicon vias are etched on the substrate layer to reach the pads on the device layer for electrical connection.

Fig. 1: The structural design of the microsensor and the principle of volume compressed sensing.
figure 1

a The resonant high pressure microsensor comprises a SOI wafer with resonators and vias, and a silicon wafer as cap for vacuum packaged. b The resonators anchor to the bulk of SOI and silicon cap through micro-beams and by modifying the micro-beams, two resonators behave different sensitivities to pressure. c While under pressure, the volume of the microsensor would be compressed, and the compressed deformation generates axial stresses on resonators through micro beams

Full size image

The principle of volume compressed sensing is shown in Fig. 1c. The resonators are connected to the anchors by micro-beam supports, and unlike the diaphragm sensing, the anchors are bonded to both the substrate layer of SOI and the silicon cap. There are only small chambers for resonators and gas getters, and the size of chambers are minimized as possible, so that the microsensor would be compressed as a bulk while under pressure without any deformation similar to diaphragm, and a uniform internal stress occurs in the microsensor, producing the frequency shifting of both resonators. The relation between the given pressure and stress is expressed by the following equation27:

$${\varepsilon }_{s}=-\frac{1}{3{Y}_{B}}P$$
(1)

Where \({Y}_{B}\) is the bulk modulus, for silicon \({Y}_{B}=9.8\times 1{0}^{10}{Pa}\)27, \(P\) is the external pressure, \({\varepsilon }_{s}\) is the average strain in microsensors caused by external pressure. As pressure has been applied on all six faces of the microsensor, according to the deformation compatibility equation:

$${\varepsilon }_{{sx}}={\varepsilon }_{{sy}}={\varepsilon }_{{sz}}={\varepsilon }_{s}$$
(2)

Assuming a clamped-clamped beam (C-C beam) as a resonator is located inside the microsensor, and its axial direction is along with the x-axial of microsensor, according to deformation compatibility equation:

$${\varepsilon }_{R}={\varepsilon }_{s}$$
(3)

Where \({\varepsilon }_{R}\) is the strain on the axial direction of the resonator, Therefore the axial stress \({\sigma }_{l}\) on resonator is as bellow:

$${\sigma }_{R}=E{\varepsilon }_{R}=-\frac{E}{3{Y}_{B}}P$$
(4)

Considering a resonator subjected to stress \({\sigma }_{R}\), the frequency under this condition is outlined below.

$${f}_{\sigma }={f}_{0}\sqrt{1+\frac{{\sigma }_{R}}{{\sigma }_{c}}}$$
(5)

The resonator’s inherent frequency is denoted by \({f}_{0}\) while the critical Euler stress is represented by \({\sigma }_{c}\), Simplify the Eq.(5) that,

$${f}_{\sigma }={f}_{0}\left(1+\frac{{\sigma }_{R}}{2{\sigma }_{c}}\right)={f}_{0}-\frac{{f}_{0}E}{6{\sigma }_{c}{Y}_{B}}P$$
(6)

It indicates that in a resonant pressure microsensor without diaphragm, the sensitivity of the frequency of a particular C-C resonator shifts along with pressure in a sensitivity as below:

$$S=\frac{\Delta f}{{f}_{0}\Delta P}=-\frac{E}{6{\sigma }_{c}{Y}_{B}}$$
(7)

Micro-beam supports

From (7), In order to achieve temperature compensation with dual resonators, additional structures are necessary to achieve different pressure sensitivities for the two resonators Through the innovative structural designs of micro-beam supports, different stress distributions are generated approaching the resonators that results in different pressure sensitivities. The structures of micro-beam supports are shown in fig. 2. Defined the axial direction of a resonator as x-axis, and the y-axis is perpendicular to the x-axis. \(\theta\) is the angle between positive x-direction and the micro-beams and it’s around 90 degrees. Resonator I and Resonator II both takes a couple of T-type micro-beam supports but with different angles \(\theta\). Resonator I is insensitive to pressure with \(\theta\, > \,90^{\circ}\) and on the contrary Resonator II with \(\theta\, < \,90^{\circ}\) is sensitive to pressure. To analysis the effects of the micro-beams on the axial stress of the resonators, the compressed deformations on both the directions of parallel and vertical to the axes of the resonators should be taken into consideration. According to the principle of superimposed, the stresses on the resonators generated by compression deformation in two directions can be separately considered, and the total stress can be calculated by superposition;

Fig. 2: Theoretical analysis and finite element analysis of the pressure sensor with highly-integrated sensitive microelectrodes.
figure 2

a Structure of resonators with micro-beam anchors. b, c The equivalent model for x direction and y direction. d The simulated pressure sensitivities of dual resonators. e The simulated temperature disturbances of dual resonators

Full size image

For the x direction, the model can be simplified based on symmetry as shown in Fig. 2b, A and B are the two ends of a micro support beam, which can only move in x-axis. Both A and B are considered as fixed supports as the bending of the micro-beams is the main deformation with a \(\theta\) around 90 degrees.

When a pressure applied, the deformation of micro-beam can be described with (8)

$$\Delta {x}_{A}-\Delta {x}_{B}={w}_{x}$$
(8)

Among them \({w}_{x}\) is the deflection deformation of the micro beam in the x direction. \(\Delta {x}_{A}\) and are the To write the expression for deflection, consider point A with no displacement and point B as subjected to support reaction force \({F}_{B}\) when there is a stress \({\sigma }_{R1}\) on the resonator,

$${w}_{x}=\frac{{F}_{B}{l}^{3}}{6E{I}_{s}}\cdot \frac{1}{{\rm{si}}{{\rm{n}}}^{2}\theta }$$
(9)

Where,

$${F}_{B}=\frac{{\sigma }_{R1}{BH}}{2},{I}_{s}=\frac{{b}^{3}h}{12}$$

According to the principle of volume compression, since there are only very small cavities inside, the average strain in the x-direction between two anchors for overall compression deformation is expressed as follows:

$$\bar{{\varepsilon }_{x}}=\frac{2\Delta {x}_{A}}{L+2l\cot \theta }=-\frac{1}{3{Y}_{B}}P$$
(10)

For a resonator, the average strain on the resonator is:

$${\bar{\varepsilon }}_{R1}=\frac{2\Delta {x}_{B}}{L}=\frac{{\sigma }_{R}}{E}$$
(11)

Substitute (9), (10), and (11) into (8):

$$-\frac{\left(L+2l\cot \theta \right)P}{6{Y}_{B}}-\frac{L{\sigma }_{R1}}{2E}=\frac{B{l}^{3}}{E{b}^{3}}\frac{1}{{\rm{si}}{{\rm{n}}}^{2}\theta }{\sigma }_{R1}$$
(12)

As \(2l\cot \theta \ll L\), (12) can be simplified:

$${\sigma }_{R1}=-\frac{E}{3{Y}_{B}\left(\frac{2B{l}^{3}}{L{b}^{3}}\frac{1}{{\rm{si}}{{\rm{n}}}^{2}\theta }+1\right)}P$$
(13)

On the y-axis, the model can also be simplified based on symmetry as shown in Fig. 2c. Point A can only move in y-axis with \(\Delta {y}_{A}\) and the Point B can only move in x-axis with \(\Delta {x}_{B2}\). On the contrary, both A and B are considered as simple supports as the bending of the micro-beams can be ignored with a \(\theta\) around 90 degrees.

As the micro beam has been seen as a rigid rod and the small change of angle under compression can be ignored, so that:

$$\left(l+\Delta {y}_{A}\right)\cot \theta =l\cdot \cot \theta +\Delta {x}_{B2}$$
(14)

Similar to (10) and (11), the average strain in the y-direction between two anchors and the average strain on the resonator are shown below:

$$\bar{{\varepsilon }_{y}}=\frac{\Delta {y}_{A}}{l}=-\frac{1}{3{Y}_{B}}P$$
(15)
$${\bar{\varepsilon }}_{R2}=\frac{2\Delta {x}_{B2}}{L}=\frac{{\sigma }_{R2}}{E}$$
(16)

Substitute (15) and (16) into (14) and simplified:

$${\sigma }_{R2}=-\frac{2{lE}}{3L{Y}_{B}}\cot \theta \cdot P$$
(17)

Considering the stress generated by compression deformation in the two directions mentioned above, the total stress on the resonator is:

$${\sigma }_{R}={\sigma }_{R1}+{\sigma }_{R2}=-\frac{E}{3{Y}_{B}}\left({\beta }_{x}+{\beta }_{y}\right)P$$
(18)

Where

$${\beta }_{x}=\frac{1}{\left(\frac{2B{l}^{3}}{L{b}^{3}}\frac{1}{{\rm{si}}{{\rm{n}}}^{2}\theta }+1\right)},{\beta }_{y}=\frac{2l}{L}\cot \theta$$

Substitute (18) into (6) :

$${f}_{\sigma }={f}_{0}\left(1-\frac{E}{3{Y}_{B}}\frac{{\beta }_{x}+{\beta }_{y}}{2{\sigma }_{c}}P\right)$$
(19)

So the pressure sensitivity \(S{\prime}\) of resonator with micro-beams is as followed:

$$S^{\prime} =\frac{\Delta f}{{f}_{0}\Delta P}=-\frac{E}{6{\sigma }_{c}{Y}_{B}}\left({\beta }_{x}+{\beta }_{y}\right)$$
(20)

According to (20), as \({\beta }_{x}\, > \,0\), when \(\theta \,< \,90^{\circ}\), \({\beta }_{y}\, > \,0\), so that a negative pressure sensitivity is obtained. On the other hand, once \(\theta \,> \,90^{\circ}\), \({\beta }_{y}\, < \,0\), as a result there is a possibility that the pressure sensitivity could be around zero, which is insensitive to pressure, with specific structural parameters. Based on this theoretical analysis, the geometric parameters are determined as Table 1. With these geometric parameters, a finite element analysis has been done. Figure 2d, e show the simulated pressure sensitivities and temperature disturbances of two resonators.

Table 1 The key geometric parameters and the theoretical and simulated pressure sensitivity
Full size table

Fabrication

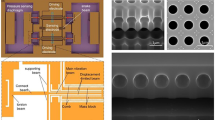
In Fig. 3a, the process of manufacturing high-pressure resonant microsensors utilizing bulk silicon technology are depicted. As shown in Fig. 3a, the processes i) to vi) of DRIE, oxide layer removed and the eutectic bonding are the same as previous work25,28. The resonator’s structure is depicted in Fig. 3b, while the cross-sectional view of the resonators is presented in Fig. 3c. Additionally, the different micro-beam structures of the two resonators are illustrated in Fig. 3d, e. Then, a patterned BF33 wafer as stress-isolated structure is produced in vii) and viii) by gaseous hydrofluoric acid with Au/Cr mask.

Fig. 3: The processes of manufacturing and the images of high-pressure microsensors.
figure 3

a The schematic of manufacturing process of the high-pressure microsensors includes key steps of i) vias etching, ii) device layer etching, iii) oxide layer removing, iv) sputtering, v) lithography and etching, vi) sputtering, vii)-viii) etching of iso-structure, ix) eutectic bonding for vacuum packaged, x) anodic bonding, xi) scribing and wire bonding. b The resonator on the device layer of the SOI. c The SEM image of cross-section through A-A plane. d, e The SEM image of micro-beams of Resonator I and II. f Three views of the chip of microsensors

Full size image

The iso-structure is bonded to the silicon cap by wafer anodic bonding and the fabricated wafer-level resonant pressure microsensor is scribing into chips, The images of microsensors are shown in Fig. 3e with the scale of 3.3 mm × 3.3 mm × 1.6 mm.

In order to verify the characteristics and enhance the environmental adaptability of developed microsensors, the microsensors were oil-filled encapsulated15,29. the microsensors in chips were fixed on a stainless base for wire bonding, surrounded by silicone oil and sealed with a corrugated diaphragm. Figure 4a shows the cross-section of a microsensor sealed in an oil-filled isolated structure. A patterned ceramic was placed around the chip to reduce the volume of the silicone oil for a reduced temperature disturbance from the silicone oil. The oil-filled encapsulation process is as bellowed: First, the microsensor and the ceramic were pasted onto the base. Then, the electrical connections from the microsensor to each pin were formed through wire bonding. Subsequently, the base, the corrugated diaphragm, and the ring were stacked in sequence and then formed by laser welding. The silicone oil immersion and filling were carried out under high vacuum conditions. Finally, a sealing pin was pressed in to seal the oil filling hole, forming the oil-filled isolation encapsulation. The microsensor after oil-filled sealing has six pins, including DC bias, the driving and detection of the two resonators, as well as the grounding.

Fig. 4: Oil-filled packaging and basic characteristics of microsensors.
figure 4

a The cross-section of oil-filled isolated structure of microsensors and the sealed microsensors. b The test system of high pressure microsensors. c, d Pressure sensitivity and temperature disturbance characterization of the developed high-pressure microsensors where the horizontal axis represented the pressure and temperature, and the vertical axis represented frequency of resonators

Full size image

Results and discussion

A closed-loop measurement has been conducted using a DC bias voltage of 15 V. Figure 4b shows the test system of microsensors. The piston manometer(BHY-160B) provides a hydraulic pressure up to 70 MPa with an accuracy of 0.005%. The temperature chamber(SU-262) provides different temperature conditions. The microsensor will send the frequency of two resonators and pressure back to host computer.

Figure 4c, d shows the pressure sensitivity and temperature disturbance characteristic with a pressure range of 0.1 ~ 70 MPa and a temperature range of −10 ~ 50 °C. Pressure sensitivities of resonators are quantified as 0.003 kHz/MPa ( ~ 30 ppm/MPa) for Resonator I and −0.118 kHz/MPa (~−1311 ppm/MPa) of Resonator II under 20 °C. Temperature disturbances of the two resonators are −1.270 Hz/°C ( ~ −12.2 ppm/°C) and −0.943 Hz/°C ( ~ −9.75 ppm/°C).

As shown in Fig. 4c, d, the pressure sensitivity of Resonator I is so small compared to temperature disturbance that Resonator I can be considered insensitive to pressure, the functions F1 and F2 are employed to describe how the frequencies of the resonators are affected by temperature or pressure. Specifically, F1 represents the relationship of the frequency of the Resonator I with temperature, while F2 represents the relationship of the frequency of the Resonator II with both pressure and temperature:

$$\left\{\begin{array}{c}{f}_{1}={F}_{1}\left(T\right)\\ {f}_{2}={F}_{2}\left(P,T\right)\end{array}\right.$$
(21)

So there is:

$$P={G}_{2}\left({f}_{2},{G}_{1}\left({f}_{1}\right)\right)$$
(22)

Where \({G}_{1}\) and \({G}_{2}\) are \({{F}_{1}}^{-1}\) and \({{F}_{2}}^{-1}\). Therefore, a polynomial surface, as expressed in (23) is utilized to approximate the measurement outcomes of the high-pressure resonant pressure microsensor, enabling temperature compensation within a pressure range spanning from 0.1 MPa to 70 MPa and a temperature range of −10 °C to 50 °C.

$$P=\mathop{\sum }\limits_{i=0}^{5}\mathop{\sum }\limits_{j}^{5-i}{a}_{{ij}}{{f}_{1}}^{i}{{f}_{2}}^{j}$$
(23)

It yields a fitting error within the range of ±7 kPa and demonstrates a fitting accuracy exceeding 0.01%FS, as depicted in Fig. 5a. Utilizing the fitting coefficients, Fig. 5b illustrates the measurement errors at temperature conditions of −10 °C, 20 °C, and 50 °C, with an accuracy better than 0.01%FS at these temperatures.

Fig. 5: The characteristics of microsensors.
figure 5

a Fitting errors from 0.1 to 70 MPa and from −10 to 50 °C by polynomial algorithm. b Measurement errors under different temperature conditions of −10 °C, 20 °C, and 50 °C. c Response time of the microsensor from beginning to 63% step pressure. d Resolution characterization of the developed high-pressure microsensor at 20 °C

Full size image

The response time was characterized with a pre-filled chamber with a pressure of 10 MPa and a quick-opening valve. The high-pressure microsensor was connected to the outlet of an electrically controlled quick-opening valve. The inlet of the valve was connected to a pressure chamber, and a high-precision pressure controller was used to control the pressure in the chamber to an accurate value of 10 MPa. After the pressure stabilizes, trigger the valve via an electrical signal to achieve a rapid pressure step. The sensor was connected to a high-speed data acquisition system with a sampling rate of 1000 Hz. When a step-change in pressure was applied to the sensor, the output of the sensor was continuously recorded. The results showed in Fig. 5c that it takes 6.23 ms for the sensor reading to rise from beginning to 63% step pressure, indicating sufficient dynamic performance. A high-precision pressure controller PPC4 that could generate small pressure changes was used to evaluate the resolution of the sensor. The pressure changes were incremented in different steps of \(\Delta P\) from 7 kPa to 100 Pa. The output of the sensor was recorded for each pressure steps. As shown in Fig. 5d, when the pressure changes to 100.1 kPa, the minimum value of the sensor output is greater than the maximum value when the pressure is 100.0 kPa. Therefore, a resolution of 100 Pa can be achieved. There is a certain deviation between the output value and the actual pressure value. This is because the sensor is designed with a measuring range of 70 MPa. Even with an accuracy of 0.01% FS, its absolute error is still relatively large.

Conclusion

A theoretical model is established for micro beams. The expression for pressure sensitivity of micro-beam supported resonators under the principle of volume compression sensitivity has been derived, and the theoretical results of pressure sensitivity are consistent with the simulation results and actual characteristic of microsensors. The micro-beam supports have been proved of great significance for stress reduction to protect resonators from buckling in previous work, and in this paper a quantitative relationship has been established between the geometric parameters of micro-beam structures and the pressure sensitivity of microsensors, providing guidance for design of high-pressure microsensors.

Based on the theoretical model, a resonant high-pressure microsensor with dual resonators based on volume compressed sensing is designed, fabricated and characterized experimentally. The two resonators in one bulk microsensors compressed by pressure can perform different pressure sensitivities as familiar as theoretical analysis, which make it possible to realize a temperature self-compensation. The developed microsensor performed in a similar way to the designed characterization and exhibited a high measurement accuracy of 0.01% FS (0.1 to 70 MPa) under full temperature range (−10 to 50 °C). And with an oil-filled isolating structure, the microsensors can deal with complex hydraulic environments. It shows that the resonant microsensors based on volume compressed sensing with micro beams take advantages of high strength, high accuracy, excellent resolution and sufficient dynamic performance.