Introduction

Entanglement is one major resource any quantum protocol utilizes to achieve quantum advantage1,2. Generally, the entanglement is created by unitary operations, where dissipation is considered detrimental and should be maximally avoided. Inspired by laser cooling, an alternative approach is to use tailored dissipation for stabilizing entanglement. By coupling the qubit system to some cold reservoirs, one can engineer the Hamiltonian such that the population will flow directionally to the stabilized point in the Hilbert space, and extra entropy is autonomously dumped into the cold reservoir during the process. This provides an extra route to state preparation. In a multiqubit-reservoir coupled system, dissipation engineering can enhance the capabilities of quantum simulation, as predicting the final state of a driven dissipative quantum system is more complex than its unitary counterpart3 when all local qubit and reservoir interactions are simultaneously turned on. Dissipation stabilization also inspires autonomous quantum error correction codes (AQEC)4,5,6,7,8,9 that achieve hardware efficiency in the experiment.

Stabilization has been theoretically proposed and experimentally realized in different platforms, such as superconducting qubits10,11,12,13,14,15,16,17 and trapped ions18,19, focusing on stabilizing a single special state per device, such as even or odd parity Bell states. Unlike universal quantum state preparation through unitary gate decomposition, dissipative stabilization requires individual Hamiltonian engineering for each stabilized state through different drive combinations or hardware. This makes the tunable dissipative stabilization a challenging task. A generalized scheme that allows one to programmatically choose stabilized states from a large class of states per device will expand the toolbox for state preparation. For instance, the ability to choose an arbitrary stabilized state can be used for the implementation of density matrix exponentiation20,21 by enabling an efficient reset of the input density matrix.

In this work, we realize an autonomous stabilization protocol with superconducting circuits that allows selection from a broad class of states, including the maximally entangled states. We use microwave-only drives with tunable parameters such as drive detunings and strengths that allow fast programmable switching between Bell states of different parities. The system is based on a two-transmon inductive coupler design8,17,22,23 that allows fast parametric interactions between qubits without significantly compromising their coherence. The readout resonators are also used as cold reservoirs, eliminating the requirement for extra components. We perform stabilization spectroscopy and demonstrate a fidelity over 78% for all stabilized states. For odd and even parity Bell pairs, we measured 84.6% and 82.5% stabilization fidelity and a stabilization time of 1.8 μs and 0.9 μs respectively. The current stabilization protocol cannot realize AQEC, and a larger code distance between logical states is necessary8,9 for demonstrating quantum error correction. The structure of the paper is as follows. First, we explain the Hamiltonian construction of the stabilization protocol. Then we discuss the experimental measurement of individual stabilized state and demonstrate a dissipative switch of Bell state parity.

Results

Stabilization theory

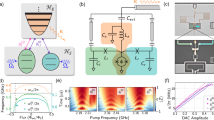
We consider a system of two coupled qubit-resonator pairs {Q1, Q2} and {R1, R2}. The lossy resonators serve as both cold baths and dispersive readouts for the qubits. We label the ground and the first excited states of the qubits Q1/2 as \(\left\vert g\right\rangle\) and \(\left\vert e\right\rangle\), and of the resonators R1/2 as \(\left\vert 0\right\rangle\) and \(\left\vert 1\right\rangle\), with the full system state being represented as \(\left\vert {Q}_{1}{Q}_{2}{R}_{1}{R}_{2}\right\rangle\). The system Hamiltonian Hsys = HQQ + HQR1 + HQR2 includes the dominant two-qubit interaction HQQ and qubit-resonator interactions HQRj, j = {1, 2} acting as perturbations. We label the four eigenstates of HQQ as \(\{\left\vert A\right\rangle,\left\vert B\right\rangle,\left\vert C\right\rangle,\left\vert D\right\rangle \}\) with eigenenergies {EA < EB ≤ EC ≤ ED} so that \(\left\vert A\right\rangle\) is the target state to stabilize. Our stabilization scheme involves engineering a one-way flow of population to \(\left\vert A\right\rangle\) connecting all intermediate eigenstates of the system.

We now derive the energy matching requirements for an efficient stabilization protocol in our two-qubit-two-resonator system depicted in Fig. 1a. We control the form of the target stabilized state \(\left\vert A\right\rangle\) by choosing different two-qubit interaction strengths and detunings that control HQQ. We change the resonator photon energy in the rotating frame by detuning the QR interactions. The dynamics of Hsys are captured by considering the following set of eigenstates: \(\{\left\vert A\right\rangle,\left\vert B\right\rangle,\left\vert C\right\rangle,\left\vert D\right\rangle \}\otimes \{\left\vert 00\right\rangle,\left\vert 10\right\rangle,\left\vert 01\right\rangle \}\). We neglect the resonator state \(\left\vert 11\right\rangle\) as the probability of simultaneous population in both resonators {R1, R2} is extremely low when resonator decay rate κ is much larger than the qubit decay rate γ (assumed identical). The central column in Fig. 1(a) shows the eigenstates of HQQ with no photons in the resonators. The left column represents the same states with one photon in the left (R1) resonator and similarly for the right column is associated with the second resonator (R2). We engineer the photon energies in R1 and R2 to be EB − EA and EC − EA respectively through tuning the QR interactions HQRj. This condition puts two transitions \(\left\vert A01\right\rangle \leftrightarrow \left\vert C00\right\rangle\) and \(\left\vert A10\right\rangle \leftrightarrow \left\vert B00\right\rangle\) on resonance, shown in Fig. 1a. If \(\left\langle A01\right\vert {H}_{QR1}\left\vert C00\right\rangle\) and \(\left\langle A10\right\vert {H}_{QR2}\left\vert B00\right\rangle\) are non-zero, two on-resonance oscillations between \(\left\vert C00\right\rangle\), \(\left\vert A01\right\rangle\) and between \(\left\vert A10\right\rangle\), \(\left\vert B00\right\rangle\) will be created. Since both resonators are lossy, the oscillation will quickly damp to \(\left\vert A00\right\rangle\). To complete the downward stabilization path, we need to also connect \(\left\vert D00\right\rangle\) into the flow. We further require that the following terms are non-zero so that the transfer path is not blocked: \(\left\langle B01\right\vert {H}_{QR1}\left\vert D00\right\rangle\), \(\left\langle C10\right\vert {H}_{QR2}\left\vert D00\right\rangle\). If all four interaction strengths (shown in green double-headed arrows in Fig. 1a) are dominant over the qubit decay rate, populations in \(\left\vert B\right\rangle\), \(\left\vert C\right\rangle\), and \(\left\vert D\right\rangle\) will flow to \(\left\vert A\right\rangle\). From Fermi’s golden rule, the interaction strength between two states is quadratically suppressed by their energy gap and maximized when on-resonance24. This imposes a simple energy-matching requirement for efficient stabilization: ED + EA = EB + EC. Energy degeneracy within \(\{\left\vert B\right\rangle,\left\vert C\right\rangle,\left\vert D\right\rangle \}\) will not affect the stabilization scheme, because it will not block the dissipative flow to \(\left\vert A00\right\rangle\) in Fig. 1a.

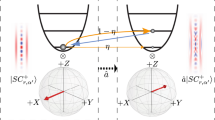
Fig. 1: Programmable stabilization protocol.
figure 1

a General stabilization scheme. Two qubits' eigenstates \(\{\left\vert A\right\rangle,\left\vert B\right\rangle,\left\vert C\right\rangle,\left\vert D\right\rangle \}\) are plotted in the energy level diagram. When the energy relation ED + EA = EB + EC is satisfied, \(\left\vert A\right\rangle\) is stabilized. Qubit-resonator interactions and resonator photon decay rate κ are shown in blue and orange arrows. Qubit decay rate γ is assumed slowest and not plotted. b Stabilization of entangled states \(\left\vert {\Psi }_{\theta }\right\rangle=\sin \left(\theta /2\right)\left\vert gg\right\rangle -\cos \left(\theta /2\right)\left\vert ee\right\rangle\) or \(\left\vert {\Phi }_{\theta }\right\rangle=\sin \left(\theta /2\right)\left\vert ge\right\rangle -\cos \left(\theta /2\right)\left\vert eg\right\rangle\). c A special case of b that stabilizes the odd and even parity bell states \(\left\vert {\Phi }_{-}\right\rangle\) and \(\left\vert {\Psi }_{-}\right\rangle\). Circulating arrows are color-coded to represent red (exchange-like) and blue (two-photon-pumping) sidebands respectively. The QQ and QR sideband rates are separate Ω and Wj, and the QR sideband is detuned in frequency by Ω/2.

Full size image

As an explicit demonstration, we first stabilize a continuous set of entangled states \(\left\vert {\Psi }_{\theta }\right\rangle=\sin \left(\theta /2\right)\left\vert gg\right\rangle -\cos \left(\theta /2\right)\left\vert ee\right\rangle\), illustrated in Fig. 1b. Here, θ can be regarded as a “blending angle" between the two even parity states \(\left\vert gg\right\rangle\) and \(\left\vert ee\right\rangle\). We introduce three sideband25 transitions into the system: qubit-qubit (QQ) blue sideband \(\left\vert gg\right\rangle \leftrightarrow \left\vert ee\right\rangle\) with rate Ω and two qubit-resonator (QR) blue sidebands \(\left\vert g0\right\rangle \leftrightarrow \left\vert e1\right\rangle\) between Qj and Rj with rate Wj. In this context, ‘sideband’ refers to a two-photon process where either a single photon is exchanged at the frequency difference (known as the red sideband) or two photons are simultaneously driven at the frequency sum (referred to as the blue sideband). To ensure that HQRj act as perturbations over HQQ, we adjust the drive strengths to satisfy Ω ≫ Wj. We further detune the QQ, QR1, and QR2 blue sideband by δ, (Δ − δ)/2, and (Δ + δ)/2 in frequencies, with \(\Delta=\sqrt{{\Omega }^{2}+{\delta }^{2}}\). The detuning δ determines the blending angle \(\theta={\tan }^{-1}\left(\frac{\delta+\Delta }{\Omega }\right)\) with a range of \([0,\frac{\pi }{2})\). In the presence of these three drives, the rotating frame Hamiltonian Hsys is

$${H}_{{{{\rm{sys}}}}}=\frac{\Omega }{2}\left({a}_{q1}{a}_{q2}+h.c.\right)+\delta {a}_{q1}^{{{\dagger}} }{a}_{q1}\\+\frac{{W}_{1}}{2}\left({a}_{q1}{a}_{r1}+h.c.\right)+\frac{{W}_{2}}{2}\left({a}_{q2}{a}_{r2}+h.c.\right)\\+\frac{\Delta+\delta }{2}{a}_{r1}^{{{\dagger}} }{a}_{r1}+\frac{\Delta -\delta }{2}{a}_{r2}^{{{\dagger}} }{a}_{r2}.$$
(1)

Here aqj and arj are separately the j-th qubit’s and resonator’s annihilation operator. Anharmonicity α is omitted from Equation (1) by treating both transmons as two-level systems. The presence of anharmonicity effectively suppresses the higher energy levels’ population in either transmon. Under the combined conditions Ω ≫ Wj ~ κ ≫ γ and Wj = W, the eigenstates with zero resonator photons are \(\{\left\vert {\Psi }_{\theta }00\right\rangle,\left\vert ge00\right\rangle,\left\vert eg00\right\rangle,\left\vert {\Psi }_{\pi -\theta }00\right\rangle \}\), with corresponding eigenenergies \(\{\left(\delta -\Delta \right)/2,0,\delta,\left(\delta+\Delta \right)/2\}\). Assuming the lossy resonator has a Lorentzian energy spectrum, the two-step refilling rate Γt from \(\left\vert eg00\right\rangle\) to \(\left\vert {\Psi }_{\theta }00\right\rangle\) (\(\left\vert eg00\right\rangle \leftrightarrow \left\vert {\Psi }_{\theta }01\right\rangle\), \(\left\vert {\Psi }_{\theta }01\right\rangle \to \left\vert {\Psi }_{\theta }00\right\rangle\)) is24

$${\Gamma }_{t}=\frac{{W}^{2}{\cos }^{2}\left(\theta /2\right)\kappa }{{\kappa }^{2}+{W}^{2}{\cos }^{2}\left(\theta /2\right)}.$$
(2)

The other two-step transitions \(\left\vert ge00\right\rangle \to \left\vert {\Psi }_{\theta }00\right\rangle\), \(\left\vert {\Psi }_{\theta -\pi }00\right\rangle \to \left\vert ge00\right\rangle\), and \(\left\vert {\Psi }_{\theta -\pi }00\right\rangle \to \left\vert eg00\right\rangle\) also have the same rate. Therefore, the steady-state fidelity \({{{{\mathcal{F}}}}}_{\infty }\) for \(\left\vert {\Psi }_{\theta }00\right\rangle\) is (ignoring all off-resonant transitions, see Supplementary Note 2 for detail)

$${{{{\mathcal{F}}}}}_{\infty }={\left(\frac{{\Gamma }_{t}+\gamma {\sin }^{2}\left(\theta /2\right)}{{\Gamma }_{t}+\gamma }\right)}^{2}.$$
(3)

Similarly, we can stabilize another set of entangled states with odd parity \(\left\vert {\Phi }_{\theta }\right\rangle=\sin \left(\theta /2\right)\left\vert ge\right\rangle -\cos \left(\theta /2\right)\left\vert eg\right\rangle\). We introduce three sideband interactions: QQ red \(\left\vert eg\right\rangle \leftrightarrow \left\vert ge\right\rangle\), QR1 red \(\left\vert e0\right\rangle \leftrightarrow \left\vert g1\right\rangle\), and QR2 blue \(\left\vert g0\right\rangle \leftrightarrow \left\vert e1\right\rangle\) with rates {Ω, W3, W4} and frequency detunings {δ, (Δ + δ)/2, (Δ − δ)/2} respectively. Under this condition, four resonant interactions will appear: \(\left\vert gg00\right\rangle \leftrightarrow \left\vert {\Phi }_{\theta }01\right\rangle\), \(\left\vert ee00\right\rangle \leftrightarrow \left\vert {\Phi }_{\theta }10\right\rangle\), \(\left\vert ee01\right\rangle \leftrightarrow \left\vert {\Phi }_{\theta -\pi }00\right\rangle\), and \(\left\vert gg10\right\rangle \leftrightarrow \left\vert {\Phi }_{\theta -\pi }00\right\rangle\). The detuning similarly sets the blending angle \(\theta=\arctan \left(\frac{\delta+\Delta }{\Omega }\right)\).

With the above construction, we create a stabilization protocol that can freely tune the blending angles. As a special case, when QQ sideband detuning δ = 0, the blending angle for both cases is \(\theta=\frac{\pi }{2}\), which corresponds to the odd and even parity Bell states \(\left\vert {\Phi }_{-}\right\rangle=(\left\vert ge\right\rangle -\left\vert eg\right\rangle )/\sqrt{2}\) and \(\left\vert {\Psi }_{-}\right\rangle=(\left\vert gg\right\rangle -\left\vert ee\right\rangle )/\sqrt{2}\), shown in Fig. 1c.

In fact, this stabilization protocol can be generalized to stabilize an even larger group of states, including both entangled and product states, as long as the energy matching requirement ED + EA = EB + EC is satisfied when engineering HQQ. The following is a list of tunable parameters to engineer HQQ: QQ sideband strength Ω, QQ sideband detunings δ, single qubit Rabi drive strength, and single qubit Rabi drive detunings. Corresponding stabilized state \(\left\vert A\right\rangle\) is determined from HQQ. Details about the stabilizable manifold are discussed in Supplementary Note 4.

Experimental results

We perform the stabilization experiment in a system with two transmons capacitively coupled to two lossy resonators (See Supplementary Note 1). Two transmons are inductively coupled through a SQUID loop. All QQ sidebands and QR red sidebands are realized through modulating the SQUID flux at corresponding transition frequencies. QR blue sidebands are achieved by sending a charge drive to the transmon at half the transition frequencies. The experimentally measured qubit coherence are T1 = 24.3 μs (9.1 μs),  TRam = 15.2 μs (9.8 μs),  Techo = 24.6 μs (14.3 μs) for Q1(Q2), and the measured resonator decay rate κ/2π are {0.33, 0.43} MHz for R1 and R2 respectively.

Figure 2 shows the time evolution of state fidelity for the odd and even parity Bell state stabilization. To stabilize \(\left\vert {\Psi }_{-}\right\rangle\), a Ω = 2π × 2.0 MHz QQ blue sideband, W1 = W2 = 2π × 0.47 MHz QR blue sidebands are simultaneously applied to the system. Both QR sidebands are detuned by Ω/2 = 2π × 1.0 MHz in frequency to implement the stabilization scheme depicted in Fig. 1(c). For each stabilization experiment, we reconstruct the system density matrix through two-qubit state tomography using 5000 repetitions of 9 different pre-rotations. The stabilization fidelity measured at 49 μs (much longer than single qubit T1 and TRam) is 82.5%. To stabilize \(\left\vert {\Phi }_{-}\right\rangle\), a Ω = 2π × 3.0 MHz QQ red sideband, W1 = W2 = 2π × 0.36 MHz QR1 red and QR2 blue sidebands are simultaneously applied to the system, with both QR sidebands detuned by Ω/2 = 2π × 1.5 MHz. The stabilization fidelity measured at 49 μs is 84.6%. The two-qubit state tomography data at 49 μs after ZZ coupling correction26 are shown for both stabilization cases. Fidelities are calculated as \(F={({\mbox{tr}}\sqrt{\sqrt{\rho }\sigma \sqrt{\rho }})}^{2}\), where σ is the target state and ρ is the tomography reconstructed density matrix. Error bars (one standard deviation) for all expectation values calculated from the Maximum Likelihood Estimation(MLE) reconstructed density matrix use the Tomographer package27.

Fig. 2: Experimental stabilization of different Bell states.
figure 2

Experimental demonstration of \(\left\vert {\Psi }_{-}\right\rangle\) (a, b) and \(\left\vert {\Phi }_{-}\right\rangle\) (c, d) stabilization with the initial state \(\left\vert gg\right\rangle\). Two-qubit state tomography is performed at each time point, and the reconstructed density matrix is used to calculate the target state fidelity. The density matrices reconstructed with 5000 single shot measurements at 49 μs are plotted. Lab frame simulation results are shown in dash lines, which matched well in both short and long time scales. Parameters used in simulation: {Ω, W1, W2, Γ1, Γ2}/2π = {2.0, 0.47, 0.47, 0.33, 0.43} MHz for \(\left\vert {\Psi }_{-}\right\rangle\) and {3.0, 0.36, 0.36, 0.33, 0.43} MHz for \(\left\vert {\Phi }_{-}\right\rangle\). Qubit coherence time is chosen as \(\{{T}_{1}^{q1},{T}_{1}^{q2},{T}_{\phi }^{q1},{T}_{\phi }^{q2}\}=\{25,12,25,25\}\,\mu\) s. Error bars (one standard deviation) are smaller than the marker size27.

Full size image

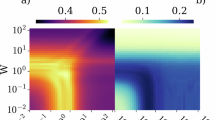
Next, we introduce QQ sideband detunings δ and stabilize more general entangled states \(\left\vert {\Psi }_{\theta }\right\rangle\) and \(\left\vert {\Phi }_{\theta }\right\rangle\). We choose the same sideband strengths ({Ω, W1, W2}/2π = {2.0, 0.47, 0.47}({3.0, 0.36, 0.36}) MHz for \(\left\vert {\Psi }_{\theta }\right\rangle\)(\(\left\vert {\Phi }_{\theta }\right\rangle\)) case) and detune QR sideband frequencies accordingly to maximize the stabilization fidelity measured at 40 μs. The experimentally measured state fidelity and state purity as a function of θ are shown in Fig. 3. Under the current QR sideband color combination, \(\left\vert {\Phi }_{\theta }\right\rangle\) fails to stabilize near θ = 180∘. This is because the interaction strength \(\left\langle gg00\right\vert {H}_{{{{\rm{sys}}}}}\left\vert {\Phi }_{\theta }01\right\rangle\) and \(\left\langle ee00\right\vert {H}_{{{{\rm{sys}}}}}\left\vert {\Phi }_{\theta }10\right\rangle\) are close to 0. Swapping QR1 and QR2 sidebands’ color and detuning performs a transformation θ → θ − π in the stabilized state. This ensures a high stabilization fidelity for arbitrary stabilization angles. Details about changing sideband colors and detunings to ensure high fidelity are presented in Supplementary Note 6.

Fig. 3: Spectroscopy of universal Bell-state stabilization.
figure 3

\(\left\vert {\Psi }_{\theta }\right\rangle\) a and \(\left\vert {\Phi }_{\theta }\right\rangle\) b are separately stabilized with a measured fidelity above 78% among different blending angle θ. The fidelities are measured after 40 μs of stabilization. For stabilizing \(\left\vert gg\right\rangle\), no external drives are applied. For \(\left\vert {\Phi }_{\theta }\right\rangle\) case, the fidelity dropped to 0 near θ = π. The dotted lines indicate simulated fidelities for the odd and even parity Bell state stabilization. All parameters used in the simulation are the same as in Fig. 2. Error bars (one standard deviation) are smaller than the marker size27.

Full size image

The flexibility in our schemes and easy access to different sidebands in our device allow a further demonstration—fast dissipative switching between stabilized states. Here, we implement such an operation that can flip the parity of the stabilized Bell pair by changing sideband combinations, shown in Fig. 1. To quantify the stabilized parity, we measure the system’s density matrix ρ and define the parity signature as \(2(| \left\langle ee\left\vert \rho \right\vert gg\right\rangle | -| \left\langle ge\left\vert \rho \right\vert eg\right\rangle | )\) describing the difference in relevant coherence parameters. The results are shown in Fig. 4. The scaling factor is chosen such that the ideal even and odd Bell pairs have parity signatures of  ± 1. Starting from the ground state \(\left\vert {Q}_{1}{Q}_{2}\right\rangle=\left\vert gg\right\rangle\), the stabilized state is set to even parity Bell pair \((\left\vert gg\right\rangle -\left\vert ee\right\rangle )/\sqrt{2}\), and we switch the parity every 20 μs. At 20 μs, the stabilized state is switched to odd parity Bell pair \((\left\vert ge\right\rangle -\left\vert eg\right\rangle )/\sqrt{2}\), and stabilization happens quickly with a time constant τr = 1.8 μs. At 40 μs, the switching from odd to even parity results in a faster stabilization with τb = 0.91 μs. The switching at 60 μs to odd Bell state shows a similar τr of 2.20 μs. We leave the stabilization drives turned on for another 25 μs to prove that the performance is not degraded after a few switching operations.

Fig. 4: Dissipative switching of Bell state parity.
figure 4

The initial state is \(\left\vert gg\right\rangle\), and the switch status is set to even parity between \(\left[0\,\mu {{{\rm{s}}}},20\,\mu {{{\rm{s}}}}\right]\) and \(\left[40\,\mu {{{\rm{s}}}},60\,\mu {{{\rm{s}}}}\right]\), and to odd parity between \(\left[20\,\mu {{{\rm{s}}}},40\,\mu {{{\rm{s}}}}\right]\) and \(\left[60\,\mu {{{\rm{s}}}},85\,\mu {{{\rm{s}}}}\right]\). Each experimental point is measured with the two-qubit state tomography. Stabilization time is calculated by fitting the parity signature to exponential decay after each switching event.

Full size image

Further improvement of the stabilized state’s fidelity is possible by reducing the transition ratio \(\frac{\gamma }{{\Gamma }_{t}}\) (from Eq. (3)) and increasing QQ sideband rate Ω for a larger energy gap. Increasing qubit dephasing time also improves stabilization fidelity (discussed in the Supplementary Note 3). To speed up the stabilization, i.e., reduce time constants, we need to increase the refilling rate Γt. Since QR sideband rate W is bounded by the QQ sideband rate Ω to ensure the validity of the perturbative approximation, given a fixed W, Γt is maximized when the resonator decay rate \(\kappa=W\cos (\theta /2)\). For the even and odd parity Bell states, further increase in both resonators’ κ compared to our current parameters would thus be beneficial. More details about stabilization robustness are discussed in Supplementary Note 3. To stabilize a more general set of states shown in Supplementary Note 4, longer qubit coherence is needed to improve the experimental resolution between different stabilized states in this manifold and is a subject of future work. Details about stabilization infidelities are discussed in Methods.

Discussion

In conclusion, we demonstrate a two-qubit programmable stabilization scheme that can autonomously stabilize a continuous set of entangled states. We develop an inductively coupled two-qubit device that provides access to both QQ and QR sideband interactions required. The stabilization fidelity among all stabilization angles is above 78%, specifically, we achieved high Bell pair stabilization fidelity (84.6% for the odd parity and 82.5% for the even parity) as two special points. We further demonstrate a parity switching capability between the Bell pairs with fast stabilization time constants (< 2 μs). To realize AQEC, the refilling rate from the error state to the logical state should be much faster than the error rate. The fast switching rate between different stabilized states, which is over an order of magnitude larger than the transmons’ decay and dephasing rate, is sufficient for AQEC. We believe such freedom in choosing stabilized states will inspire generalization to autonomous stabilization of larger systems, large-scale many-body entanglement3, remote entanglement28, and density matrix exponentiation20,21. While the current stabilization protocol cannot stabilize a logical manifold, it is possible to generalize this to new AQEC logical codewords by incorporating higher transmon levels8 or by utilizing additional transmons in future developments.

Methods

Experimental error analysis

To accurately simulate the real system, we sequentially introduce several error channels. After each addition, we calculate its contribution to infidelity by measuring the difference in the steady-state fidelity. We use the states \(\left\vert {\Phi }_{-}\right\rangle\) and \(\left\vert {\Psi }_{-}\right\rangle\) as examples, with results detailed in Table 1.

Table 1 Infidelity channels for odd and even parity Bell states stabilization
Full size table

Initially, in an ideal case, decoherence-free simulations are conducted within a Hamiltonian of dimension 2 × 2 × 2 × 2 (two levels per resonator), resulting in infidelities of 1.71% and 4.98% respectively. Subsequently, transmon T1 and Tϕ are incorporated into the system, revealing that transmon decoherence accounts for the majority of the stabilization infidelity observed in experiments. A higher transmon level is then added, extending the Hamiltonian to a dimension of 3 × 3 × 2 × 2. The contribution of transmon ZZ coupling to the stabilization infidelities is found to be less than 1%. Other error channels contribute minimally, such as leakage to the \(\left\vert f\right\rangle\) state and inaccuracies in sideband frequency calibration. The discrepancy between the theoretically predicted and experimentally measured state fidelities is primarily attributed to the thermal excitation rate in the transmons when all sidebands are active. An excitation rate of 0.9 ms in both transmons sufficiently explains these deviations in the simulation.

Tomography error bar

Error bars (one standard deviation) for all expectation values calculated from the Maximum Likelihood Estimation(MLE) reconstructed density matrix use the Tomographer package27.