Introduction

Grain refinement1,2 is arguably the most effective route to elevate the mechanical strength of single-phase metallic materials. This has in fact been pushed towards an extreme over the past three decades3,4, during which the grain size in metals has been purposely brought down to below a few tens of nanometers5. The resultant “nanocrystalline (NC) metals” achieve high (such as ~2 GPa) yield strengths (σy)5. However, these NC metals still face several nagging issues that need to be resolved. First, these materials generally lack the capacity for strain hardening, as the dislocations would readily traverse the tiny grains from one side to the other, having little opportunity to be accumulated in the grain interior to block ensuing moving dislocations5,6. This takes away a primary mechanism for work hardening in metals. NC metals are therefore prone to plastic instability such as severe strain localization. Second, the tiny grains are intrinsically unstable, such that they tend to grow upon heating as well as during plastic deformation to large strains7. Third, the GPa-level σy, while impressive for elemental metals, is not yet sufficient to excel over state-of-the-art alloys, including superstrong steels that offer σy in excess of 2 GPa8,9.

A potential way to resolve these three challenges is to seek help from alloying elements, via grain boundary segregation and precipitation strengthening — textbook mechanisms for strengthening single-phase metallic materials10. Concentrated solutes with high segregation energy have a tendency to segregate to grain boundaries (GBs) to suppress grain growth11. If the solute species has a large negative mixing enthalpy with, and a different electronegativity from, the matrix12, local chemical orders may nucleate in the grain interior, facilitating dislocation multiplication and strain hardening during plastic deformation. However, for these functions to make a marked difference, the solute content needs to be sufficiently high. As such, it would be unlikely for traditional dilute solid solutions to suffice. The required solute concentration would exceed the solubility limit in the host metal such that a second phase forms.

To get around this, we take a non-equilibrium approach in this paper to introduce ~5 at% Ni into the grain interior (forming chemical heterogeneities) and grain boundary of the TiZrNbHf system, significantly exceeding the solubility limit13 without forming any secondary intermetallic phase. We will demonstrate in the following that the complex concentrated alloy (CCA) designed as such not only imparts extraordinary strengthening effect (to near-theoretical value), but also exhibits large deformability (65% homogeneous compressive strain) with strain induced grain refinement behavior. The theoretical shear strength limit of around G/10 (G is the shear modulus) was proposed by Frenkel nearly a century ago14, and was achieved in nanowiskers15 and two-dimensional materials (e.g., graphene)16 that are free from dislocations and grain boundaries. This sets the stage for a synergistic interplay with properly selected additional solute species to resolve the three challenges mentioned above for NC metals, as outlined in the next sub-section.

Results

Alloy design strategy

The idea underlying our strategy is to combine an appropriate CCA with a carefully selected solute species, which can be exceedingly efficient/effective in resolving the three challenges, due to its desirable interplay with the constituent elements in the base CCA. A specific model system demonstrated below is the alloying of solute Ni into a TiZrNbHf CCA. This combination uses the bcc CCA to set the playground, into which a distinctly different (chemically and size-wise) element is incorporated as the additional solute. The interplay between the solute (Ni) and the principal elements (Ti, Zr, Nb, and Hf) leads to the following three synergetic effects. First, adding the “dissimilar” species (Ni) into the base CCA composed of “similar” elements ushers in enthalpic interactions in such a way that it results in local compositional undulation12 and local chemical order (LCO)17 inside the 30-nm grains. This deploys chemical inhomogeneity regions with sizes on the scale of no more than a few nanometers, which are not possible in an elemental metal or dilute solution and far less likely in the base CCA by itself. These nanometer-scale entities help to trap dislocations and promote their reaction/interlocking and accumulation (to the point of even dynamic grain refinement, see discussion later) in the NC grains upon plastic deformation. All these promote strengthening and the strain hardening ability. Second, the dissimilar Ni solutes also have a tendency to segregate to GBs in this CCA, leading to reduced GB energy18 (and hence the driving force for grain growth) as well as solute drag that suppresses boundary migration. The outcome upon large plastic deformation is astonishing: while the TiZrNbHf base alloy without Ni undergoes grain growth, the (TiZrNbHf)98Ni2 alloy shows instead grain refinement. Third, the GBs are strengthened by the segregating solutes against decohesion and dislocation emission, elevating the efficacy of grain boundary hardening (the Hall-Petch slope). These mechanisms result in a high yield strength of 2.5 GPa. In other words, the addition of solutes renders the NC CCA strain-hardenable, stable against grain growth, and extraordinarily strong; the three troubling issues with NC metals are therefore resolved simultaneously. That is, one stone kills three birds all at once.

Alloy design details

The tendency for electron charge transfer among the constituent species can be gauged by their difference in electronegativity. A large difference in electronegativity often corresponds to a strong charge transfer, sometimes even transforming some of the metallic bonds towards much stronger ionic/covalent ones19. Thus, blending in solutes with a markedly different electronegativity with the matrix constituent elements would enhance the enthalpic interaction among the atoms, which increases the degree of LCO12. In the meantime, the strong charge transfer also signals a reduced equilibrium solid solubility of the solute19, which predicts its high tendency for solute segregation to grain boundaries (GBs)20. Therefore, we use electronegativity (Pauling’s scale) difference among the elements to evaluate their tendency for LCO formation and GB segregation. We identified potentially suitable solutes (Ni, Co, Fe, Rh, Ru, Ir) that have a markedly different electronegativity relative to the matrix elements in the equiatomic TiZrNbHf alloy, and thus could induce a high tendency for solute segregation to GBs (Fig. 1a). Ni is an example of such candidates. We next evaluated the phase stability of the TiZrNbHf-X (X refers to the solute) alloys through CALPHAD (Calculation of Phase Diagrams) modeling (Fig. 1b). The introduction of Ni into the TiZrNbHf reduces the chemical potential of the base alloy, predicting a bcc solid solution. The strong chemical affinity between Ni and Zr (inferred from the large negative mixing enthalpy of −49 kJ/mol)21 suggests possible formation of nanometer-scale LCOs in the grain interior. Moreover, using density-functional-theory (DFT) calculation, the segregation energy of Ni at the GB was evaluated (see Methods for details). The corresponding average segregation energy is −1.919 eV, suggesting that Ni solutes prefer to segregate at the GBs (Supplementary Fig. 1). Besides, the strengthening energy of the GB, using the energy penalty required for boundary cleavage as a metric, was also calculated in DFT modelling (Supplementary Fig. 2). The negative value of −1.33 eV for average strengthening energy indicates that the Ni solutes will enhance the grain boundary cohesion (Fig. 1c). All of the above hint Ni as an appropriate solute for the TiZrNbHf base alloy. We will see next that Ni is indeed able to produce the desired microstructural features.

Fig. 1: Alloy design, structure and composition of the (TiZrNbHf)98Ni2 (at%) nanocrystalline alloy.
figure 1

a Electronegativity48 versus atomic radius49 of the candidate solute elements. b Normalized chemical potential of element X in the TiZrNbHf-X alloy as a function of solute (X) content, after doping one element into the TiZrNbHf base alloy, calculated using CALPHAD. c Strengthening energy of the alloy’s grain boundaries (GBs) with Ni, obtained using DFT calculation. d TEM image of the needle-shaped (TiZrNbHf)98Ni2 (atomic %, at%) sample for correlative TEM-APT analysis. e Three-dimension (3D) reconstruction of the atom probe tomography (APT) dataset for the correlative TEM-APT sample. f Overlay of (d) and (e). g 1D compositional profile measured across a nanograin (marked by an arrow in e), showing Ni-enriched (LCO cluster) regions and GBs. Source data are provided.

Full size image

We prepared nanocrystalline TiZrNbHf and the designed (TiZrNbHf)98Ni2 alloys using magnetron sputtering. Transmission electron microscopy (TEM) analysis shows that the TiZrNbHf base alloy has columnar grains of ~100 nm-width, a single-phase body centered cubic (bcc) structure (Supplementary Fig. 3), and an average composition of Ti24.9Zr25.3Nb25.1Hf24.7 (atomic %, at%). The (TiZrNbHf)98Ni2 alloy also has a columnar grain structure, with an average grain width of ~30 nm (Fig. 1d, Supplementary Fig. 4). This Ni-containing alloy remains single-phase bcc as revealed by selected-area electron diffraction (SAED) analysis. The correlative TEM-APT analysis (Fig. 1e) indicates the alloy has an average composition of Ti25.6Zr21.0Nb31.7Hf19.6Ni2.1 (at%), and the GBs are enriched with Ni with an average composition of Ti24.1Zr20.8Nb26.2Hf22.2Ni6.7 (at%). In addition, ~3 nm-diameter Ni-enriched LCOs having an average composition of Ti25.5Zr19.5Nb28.9Hf21.1Ni5.0 (at%) are uniformly dispersed within the nanograins at a high number density of ~1.9 × 1023 m−3 (Fig. 1e–g). Apparently, the CCA is well suited to respond to the Ni addition for forming local inhomogeneities. Energy-dispersive X-ray spectroscopy (EDS) analysis further confirms the Ni-enrichment at the GBs and the presence of nanometer-scale Ni-enriched LCOs in the grain interior (Supplementary Fig. 5). The HAADF-STEM and EDS images show a size distribution for the LCOs, corroborating the APT results. Atom-resolved HAADF-STEM imaging reveals that the ~3 nm-sized intragrain LCO is fully coherent with the bcc matrix, and fast Fourier transformation (FFT) pattern suggests an absence of second phase (Supplementary Fig. 6). These TEM and APT findings demonstrate that the desirable intragrain LCOs and GB modifications targeted in the alloy design have indeed been realized via the Ni-TiZrNbHf combination.

Mechanical properties

We now move on to show that Ni solutes can induce a substantial change in the properties of the NC TiZrNbHf alloy. The mechanical properties of the NC (TiZrNbHf)98Ni2 alloy have been evaluated using micropillar compression (Fig. 2a, b) and microcantilever bending (Fig. 2c, d) experiments. As references for comparison, we also tested the NC TiZrNbHf under identical conditions. The base alloy shows a yield strength (σy) of 1.3 GPa and deforms homogeneously in compression with 30% strain (Fig. 2a). Interestingly, the (TiZrNbHf)98Ni2 alloy shows a σy as high as 2.5 GPa with even higher capability of homogeneous deformation (Fig. 2a, b). Three stress-strain curves of the alloy are presented in Supplementary Fig. 7, demonstrating the repeatability of the measured properties. Supplementary Fig. 8 shows improved mechanical properties of the (TiZrNbHf)98Ni2 alloy compared with that of other HEAs with similar sample dimensions. As seen in Fig. 3 (a1–a3, b1–b3), there is no localized deformation such as shear band formation even after compression to 65% strain. We compared the true stress-strain curves and calculated the apparent strain hardening rates (Supplementary Fig. 9); the (TiZrNbHf)98Ni2 alloy shows both a higher flow stress and a higher strain hardening rate, compared to those of the TiZrNbHf base alloy.

Fig. 2: Mechanical properties of the (TiZrNbHf)98Ni2 alloy in compression and bending.
figure 2

a Compressive engineering stress-strain curves of the 1 μm-diameter micropillars prepared from the (TiZrNbHf)98Ni2 and TiZrNbHf alloys. The inset shows a (TiZrNbHf)98Ni2 micropillar before compression. b SEM images of the (TiZrNbHf)98Ni2 and TiZrNbHf pillars after compression. c Load-displacement curves of the microcantilevers prepared from the (TiZrNbHf)98Ni2 and TiZrNbHf alloys. The inset displays a (TiZrNbHf)98Ni2 cantilever before deformation. d SEM snapshot images of the (TiZrNbHf)98Ni2 and TiZrNbHf cantilevers upon deformation with identical beam deflection of 640 nm. Source data are provided.

Full size image

In bending tests where the upper surfaces of the cantilevers experience tensile deformation, the NC TiZrNbHf base alloy shows a maximum flow stress (σmax) of 3.6 GPa. Large cracks are initiated from the upper surfaces of the microcantilevers (Fig. 2d). The (TiZrNbHf)98Ni2 alloy, in comparison, achieves an ultrahigh σmax of 5.6 GPa, and crack generation is absent even at a large bending deflection of 640 nm (Fig. 2d). The upper portion of the (TiZrNbHf)98Ni2 cantilever withstands a tensile strain of 11% (measured as a reduction in the necking area). The compression and bending tests show that the (TiZrNbHf)98Ni2 alloy achieves an ultrahigh yield strength almost doubling that of the base alloy, and at the same time a much higher deformability.

In a recent work, a Nb45Ta25Ti15Hf15 (at%) CCA22 achieves an exceptionally high fracture toughness, surpassing most commercial alloys and fcc HEAs that are known for their high fracture toughness. The severe lattice distortion of bcc CCA results in retarded motion of nonscrew dislocations23. The edge-character dislocations form kink bands, which prolong nonuniform strain and increase the characteristic distance between the voids ahead of the crack tip, leading to the high toughness of the Nb45Ta25Ti15Hf15 alloy22. We performed microcantilever (pre-notched) bending tests on the NC (TiZrNbHf)98Ni2 alloy (Supplementary Fig. 10). The result shows a fracture toughness of 6.0 MPa·m1/2, compared with 4.3 MPa·m1/2 for the reference NC TiZrNbHf alloy. The fracture toughness previously measured for NC alloys24,25,26, tested using such micro-cantilever (pre-notched) tests, usually ranges from 1.5–3.5 MPa·m1/2. The NC (TiZrNbHf)98Ni2 alloy clearly shows a high fracture toughness in the class of NC alloys.

Mechanisms responsible for the all-around performance

We next use the microstructural features to explain how/why the Ni-TiZrHfNb combination is able to overcome the three difficulties we are tackling for NC metals. The evolution of the grain structure in the (TiZrNbHf)98Ni2 alloy has been monitored along with compressive strains from 20% to 65% (Fig. 3a–d). SAED analysis indicated that the (TiZrNbHf)98Ni2 alloy remained single-phase bcc structure upon deformation to various strains, without twining or phase transformation. The columnar grains are slightly curved at a strain of 20%, and the curvature increases with increasing strain to 30%. At a strain of 30%, sub-grains are observed, accompanied by a more continuous diffraction ring in the SAED pattern. At a strain of 65%, the columnar grains are refined into globular grains, which are almost equiaxed with an average diameter of ~10 nm (Fig. 3b, c). Figure 3d presents a ~ 10 nm-diameter globular grain in the deformed pillar. The TEM and SAED results indicate that the (TiZrNbHf)98Ni2 alloy deforms through the motion and massive accumulation of dislocations, which is the reason why the grains get refined at large compressive strains (see further discussion below).

Fig. 3: Structural and chemical information of the (TiZrNbHf)98Ni2 alloy after compression.
figure 3

a1–a3 Cross-sectional TEM images of the (TiZrNbHf)98Ni2 micropillars after compression to strains ranging from 20% to 65%. The bottom-right insets are the corresponding SAED pattern. b1–b3 Magnified images of the local regions indicated by the white rectangles in (a), showing that the original columnar grains are slightly curved at 20% strain, and the sub-grains are formed at 30% strain. The columnar grains are refined into globular grains at a strain of 65%. c Frequency distribution of the grain diameters in the pillar deformed to 65% strain. d Typical HRTEM image of a local region in (b3), showing a globular grain with ~10 nm-diameter observed from <001> zone axis. The inset displays the fast Fourier transformation (FFT) pattern of the white dashed rectangle in (d). e 3D reconstruction of an APT sample prepared from the (TiZrNbHf)98Ni2 micropillar with 65% strain. f 2D compositional plots of Ni in a 2 nm-thick slice from the APT dataset in (e). g Schematic illustration of dislocations as carriers for Ni solutes transportation from grain interior to grain boundaries during plastic deformation. h Schematic diagram indicating the region for APT investigation.

Full size image

The dislocation evolution in (TiZrNbHf)98Ni2 turns out to be quite different from that in traditional NC materials. In the latter, after dislocations nucleate from the GBs, they transmit through the grain interior rapidly and get absorbed by the opposite GBs6, leading to the lack of strain hardening. In contrast, the intragrain Ni-enriched LCOs in the (TiZrNbHf)98Ni2 alloy promote dislocations’ entanglement and accumulation in the grain. Atom-resolved HAADF-STEM imaging reveals the profuse interactions between dislocations and Ni-enriched LCO clusters during plastic deformation (Fig. 4b2, b3). Dislocations pile up either inside the LCO (Fig. 4b3, red arrow) or at the interface between the LCO and the matrix (Fig. 4b3, yellow arrow), but do not form loops around the cluster. This suggests that while these LCOs retard dislocation motion and elevate strength, they are still shearable and can be cut through by dislocations. The BF-STEM image of the region used for HAADF-STEM imaging in Fig. 4b2 was presented in Supplementary Fig. 11, which clearly shows edge dislocations. The deformation in bulk TiZrNbHfTa alloy was found to be dominated by screw dislocations27. It was later found that in a bcc TiNbMo CCA, the severe lattice distortion renders rugged atomic environment, which retards the motion of nonscrew dislocations23. Recently, kink bands formed by edge-character dislocations promote exceptional fracture toughness in a Nb45Ta25Ti15Hf15 (at%) CCA22. Dislocations with edge segments were also observed in a deformed bcc TiVNbHfAl10 (at%) CCA with hierarchical chemical fluctuations28. In the present (TiZrNbHf)98Ni2 alloy, the solute (Ni) is markedly different from the matrix elements, which greatly enhances the inhomogeneity and promotes lattice distortion of the alloy. It is thus reasonable to expect that, in addition to screw dislocations, edge-character dislocations also play an important role during deformation.

Fig. 4: In-situ TEM tension of the TiZrNbHf and (TiZrNbHf)98Ni2 alloys at ambient temperature.
figure 4

a1–a3 Sequential TEM images of the TiZrNbHf alloy, showing dislocations (indicated by the red dashed line) move towards a grain boundary (yellow dashed line) and pile up in front of the grain boundary region. a4, a5, Bright field (BF) and dark field (DF) (probed by selecting {110} plane) TEM images of a same deformed region, showing that a crack appears at the grain boundary region. A nanograin is enclosed by the yellow dashed lines, as recognized from the DF probing. The white dashed lines in (a1–a5) highlight a reference nanograin. b1 TEM image presenting the propagation of a crack upon loading on the (TiZrNbHf)98Ni2 alloy. b2 HAADF-STEM image and (b3), the overlay atomic strain distribution and BF-STEM image of the (TiZrNbHf)98Ni2 alloy, probed near the crack. |Z| contrast in HAADF-STEM imaging reflects mass difference, and the dark regions reveal lighter weight, representing the Ni enriched regions. c1, c2 BF and DF TEM images of the TiZrNbHf alloy after fracture, respectively, probed from the same region. d1, d2, BF and DF TEM images of the (TiZrNbHf)98Ni2 alloy after fracture, respectively, probed from the same region. The white arrows in (c2, d2) highlight the nanograins in adjacent to the crack, and the yellow arrows indicate the grains away from the crack.

Full size image

Fracture toughness is directly proportional to flow stress and strain to failure22. In the (TiZrNbHf)98Ni2 alloy, the severe lattice distortion and LCOs retard dislocation motion, promoting a high yield strength. During plastic deformation, they promote the multiplication of dislocations in the nanograins, elevating the flow stress. Besides, GB cohesion is improved through Ni segregation (Fig. 1c), which impedes crack propagation and contributes to prolonged deformation, increasing the fracture strain. Consequently, the (TiZrNbHf)98Ni2 alloy achieves an enhanced fracture toughness relative to that of the base alloy.

The defect accumulation and grain refinement behavior above are distinctly different from that in the TiZrNbHf base alloy, in which we observe grain growth after compression (Supplementary Fig. 12). Upon tensile pulling to fracture of the TiZrNbHf sample, we also observe that the orientations of the nanograins become similar near the fracture surface (Fig. 4c1, c2), indicating grain rotation induced grain growth7. Such dynamic grain growth has often been observed in nanocrystalline alloys upon loading29. As shown above, (TiZrNbHf)98Ni2 showed grain refinement instead. This stark contrast is because now the Ni solutes in the grain interior segregate towards the GBs, including the newly formed ones during deformation. Dislocations appear to provide the pathways for sufficiently fast transport of the segregating solutes. We acquired chemical information from the (TiZrNbHf)98Ni2 pillar after compression to 65% strain using APT (Fig. 3e, f). The needle-shaped sample used for APT analysis was prepared in such a way that the upper region is in the deformed pillar and the lower part is in the original material, as schematically shown in Fig. 3h. In the deformed pillar, the GBs are enriched with Ni (Fig. 3e, f), and the Ni content inside of the grain is lower than that of the undeformed regions (Fig. 3f, less yellow-colored regions in the deformed pillar). The statistical concentration histogram of Ni in Supplementary Fig. 13 confirms the compositional changes upon deformation. These results suggest that Ni solutes are transported from the grain interior to the GBs of the (TiZrNbHf)98Ni2 alloy during plastic deformation. Dislocations are in fact known to serve as short-circuit channels for solutes to transport towards energetically favorable positions30, such as GBs (see schematic in Fig. 3g illustrating Ni solutes being transported from the grain interior and the LCOs to the newly formed GBs). The solute relocation is accomplished due to the short transportation distance for Ni solutes in the nanometer-sized grains. This segregation provides a mechanism that dynamically enhances the stability of the newly formed ~10 nm-diameter globular grains, rather than deformation-induced grain growth.

DFT modelling confirms a reduction of grain boundary energy by Ni segregation. Specifically, Ni segregation enhances the stability of the GBs by reducing its energy, that serves as the thermodynamic driving force for grain growth, and kinetically suppresses the GB motion via solute dragging. Grain growth is prohibited as a result. This explains why the (TiZrNbHf)98Ni2 alloy shows grain refinement (Fig. 4d1, d2), in opposite to the grain growth for the TiZrNbHf reference alloy (Fig. 4c1, c2). We also evaluated the effect of Ni segregation on the thermal stability. The (TiZrNbHf)98Ni2 and TiZrNbHf alloys were annealed at 500 oC for 1 hour, and at 600 oC for 100 h (Supplementary Fig. 14). The base alloy experiences grain growth from the original 100 nm to over 200 nm, while the (TiZrNbHf)98Ni2 alloy shows unchanged grain size after annealing at 500 oC for 1 hour. With an increase of temperature to 600 oC and prolonged annealing time to 100 h, the original columnar grains in the TiZrNbHf alloy have become globular grains, while some of the columnar grains are maintained in the (TiZrNbHf)98Ni2 alloy. The (TiZrNbHf)98Ni2 alloy shows a much smaller grain size (~50 nm) compared to that of the TiZrNbHf base alloy (~150 nm).

For the TiZrNbHf base alloy, Fig. 4a1–a3 shows that a dislocation (indicated by the red dashed line) quickly traverses the nanograin and gets absorbed by the grain boundary. Subsequently, a crack initiates from this GB region at t = t0 + 42 s (Fig. 4a4, a5), likely due to GB decohesion. In contrast, the (TiZrNbHf)98Ni2 alloy shows no preferential crack initiation from the GB region even at larger stresses and larger tensile strains (Fig. 4b1), suggesting a higher resistance against GB decohesion than that of the reference TiZrNbHf alloy. This observation is corroborated by our DFT calculation results (Fig. 1c), which indicate that Ni increases the GB cohesion of the TiZrNbHf alloy. The effects on elevating the strength of the NC alloy will be elaborated further in the next sub-section.

Our key discovery is that “small amount of solutes” can produce “big effects”, without adverse effects from brittle precipitates. To make this happen, the essential ingredient is a solute species into the base CCA, i.e., Ni + TiZrNbHf, while each alone cannot cut it. Note that a CCA is normally based on “similar” elements, which by themselves would not be able to produce the (three) effects discussed below. However, with the CCA as the NC matrix, desirable nanostructures and properties emerge with only a minor addition of solutes, thanks to the favorable interplay of the distinctly different Ni species with the base elements in the CCA.

The reasons for employing the CCA-solute combination are multi-fold. First, only when both are present, i.e., only when markedly different elements co-exist, can solute (in this case Ni)-enriched LCOs form. These intragrain inhomogeneity regions are needed to elevate strength by blocking dislocations, imposing additional energy barrier against dislocation motion from a more energetically favorable location to an unfavorable one31,32. The rate of strain hardening is enhanced as well, as can be seen in the true stress-true strain curve (Supplementary Fig. 9). This is because, the dislocation lines fighting through Ni-enriched LCOs have to increase their waviness and inevitably run into one another. Some tangled/trapped dislocations thus get stored inside the grains, reorganizing into boundaries to dynamically refine the grains.

Second, it is the presence of multiple principal components in the CCA grains that makes the diffusion sluggish to begin with, such that the smaller species Ni has adequate time (especially when through dislocation pipe diffusion) to accomplish the segregation to the GBs, which would otherwise run away if it were for a pure NC metal. Then GB migration would take off too easily for any solute segregation to catch up with. Holding down the GBs may also require a lot more solutes, which would likely cause precipitation of an unwanted second phase. Again, the solute Ni, bringing with it a pronounced difference in chemistry and atomic size, has the propensity to segregate to the GBs to reduce the GB energy by a large margin (see DFT calculation in Fig. 1c), which reduces the driving force for grain growth. The solute drag on the boundaries kinetically retards grain growth as well.

Third, the TiZrNbHf CCA provides a well-behaved baseline material that not only has a high σy (~1 GPa) to begin with but also deforms with ample dislocation activities (in fact most high-strength bcc CCAs with tensile ductility are based on the Ti-Zr-Nb-Hf system)33. In terms of yield strength, note that solid solution hardening due to the misfit of Ni solutes (assuming 2 at%) would add at most 200 MPa, according the Curtin’s formula (see Methods for details), particularly when much of these solutes aggregate to LCOs and GBs. For micrometer-grained alloys, solid solution strengthening is highly effective in enhancing the strength. Solid solution strengthening also contributes to NC alloys, yet it is far from enough to elevate the strength to the observed level, as GBs also play a crucial role. The increase of strength (from 1.3 to 2.5 GPa, as shown in Fig. 2) is therefore from another two contributors, apart from solid solution. One is the grain size difference (from 100 nm to 30 nm) between the TiZrNbHf base alloy and the (TiZrNbHf)98Ni2 alloy. This factor, based on the Hall-Petch coefficient (the Hall-Petch slope, K) of 240 MPa·μm−1/2 established by Juan et al.34, contributes ~600 MPa. The other factor is the elevation in K after the decoration of the GBs by the high-modulus Ni. In other words, the yielding of NC metals requires the re-nucleation of dislocations from their GBs, which are now hardened by Ni segregation4. K is therefore increased, relative to the GBs in the base alloy. From the Hall-Petch relationship, we know that the strength is proportional to Kd-1/2, where d is the grain size. The first derivative, dσy/dK, i.e., the strength increase due to an escalation of K, scales with d-1/2, which becomes very effective at small d. In other words, although the Ni content segregated to GB, and the resultant increase in K, may not be very large, its effect on σy gets magnified by the 30-nm grain size we are working with. Taken together, the yield strength is elevated after adding Ni, strikingly, from 1.3 GPa to 2.5 GPa (see comparison in Fig. 2).

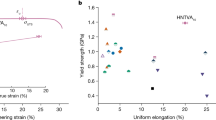
The NC (TiZrNbHf)98Ni2 alloy achieves a yield strength of 2.5 GPa (σy) which corresponds to a τy (shear stress for the initiation of plastic flow)35 of 1.25 GPa. The shear modulus (G) of the alloy is 39 GPa, calculated based on the elastic modulus measured using nanoindentation. The τy/G ratio of the NC (TiZrNbHf)98Ni2 alloy reaches 1/31, approaching the theoretical shear strength limit14. We anticipate numerous applications related to the alloy’s ultrahigh strength and deformability, for example as high wear-resistance coatings for cutting tools. Furthermore, the above-mentioned alloy design concept should guide the design of other materials. We note that a HfNbTiVAl10 alloy with three-dimensional hierarchical chemical fluctuations (HCFs) achieves an enhanced strength and tensile ductility synergy compared with the Al-free HfNbVTi alloy28. The strong bonding among the atoms of different species with negative mixing enthalpy promotes a high strength. Besides, the HCFs retard dislocation motion, which increases the opportunities of dislocation entanglement and multiplication, enhancing strain hardening and tensile ductility. Hence, it is reasonable to expect that, through utilizing the favorable interplay of the distinctly different species with the base elements in the CCA, which promote intragrain LCOs and GB segregation (enhancing GB cohesion), the alloy’s strength and tensile ductility can be simultaneously improved. This can be hinted from the microcantilever bending tests (Fig. 2c, d) where the (TiZrNbHf)98Ni2 cantilever shows a higher deformability than that of the TiZrNbHf base alloy.

The (TiZrNbHf)98Ni2 alloy in the present work was prepared using magnetron sputtering with a cooling rate above 108 K/s36, and the high cooling rate promotes a NC structure. Mechanical alloying11,37 or severe plastic deformation4,38 are also known for preparing NC samples; in those approaches suitable solutes (with electronegativity markedly different from those of the matrix) can also be introduced with an amount that is sufficient to promote LCOs and GB segregation, while avoiding the formation of second phases. The NC alloys can be annealed at an intermediate temperature to further promote the formation of LCOs. We would like to emphasize that the intragrain LCOs and enhanced GB cohesion may also benefit micrometer-grained bulk cast alloys, which requires future exploration.

In sum, this work advocates an alloy design strategy to simultaneously achieve work hardening ability, stabilized grain structure against (deformation-assisted) grain growth, and extraordinary strength, for NC alloys. The success of this approach is demonstrated using a judiciously selected CCA-solute combination: alloying species (Ni) markedly different from the constituent principal elements, into a suitable base CCA (TiZrNbHf). The interplay between the solute and the CCA ingredients spontaneously generates the intragrain LCOs to facilitate strain hardening, brings forth the GB segregation to suppress grain growth, and causes GB hardening for strength elevation, all at the same time. The resultant solute-into-CCA NC alloy is thus extraordinarily strong yet highly deformable, and self-tuned to guard against instabilities.

Methods

Materials fabrication

The (TiZrNbHf)98Ni2 and TiZrNbHf alloys were prepared using magnetron sputtering. The substrates were Si (001) wafer and the background vacuum was 10−5 Pa. The depositions were performed with a substrate bias voltage of −50 V and an Ar pressure of 0.2 Pa. The (TiZrNbHf)98Ni2 alloy was fabricated through co-sputtering with an equiatomic TiZrNbHf alloy target (99.9% purity) and an equiatomic TiZrHfNi alloy target (99.9% purity), and then annealed in the sputtering chamber at 10−5 Pa and 350 oC for 1 h. The TiZrNbHf base alloy was deposited using the equiatomic TiZrNbHf alloy target. The alloy films have a thickness of ~4 μm.

Thermodynamic modeling

The thermodynamic calculations were carried out using the Thermo-Calc Software 2021a with the TCHEA3 database, which was specifically designed for high-entropy alloys. The stability of the bcc phase was evaluated by the change of the chemical potential (μ) after introducing the solute element.

Chemical potential (μ) is defined as the chemical energy (Uc) for 1 mol of substance, \(\mu=\,\frac{{U}_{c}}{N}\), where \(N\) is the number of moles of the substance. Within the Calphad method, Gibbs free energy (G) is regarded to be equivalent to chemical energy (Uc), hence, \(\mu=\,\frac{G}{N}\).

The underlying assumption is that for a simple system without the consideration of surface, electric, magnetic, and non-hydrostatic mechanical energy contributions, the total internal energy (U) is equal to the summation of thermal (Ut), mechanical (Um), and chemical energies (Uc), U = Ut + Um + Uc, where Ut = T × S, Um = -pV, and Uc = μN. These are the fundamental equations of thermodynamics formulated by Gibbs, combing the first and second laws of thermodynamics. Hence, G = Uc = U – TS + pV, the chemical potential μ = G/N is derived from the existing G information at the given composition within the commercial thermodynamic databases TCHEA3.

Density-functional-theory (DFT) calculation of grain boundary (GB)

Five independent random solid-solution TiZrNbHf samples containing 480 atoms with a ∑5(310)[001] grain boundary (GB) was constructed as special quasi-random structure (SQS)39 (see Supplementary Fig. 2). Within the GB region (total 100 atoms) of each configuration, 5 atoms (corresponds to 5% Ni in the GB region) are randomly replaced by Ni atoms to model the corresponding Ni segregation. The atom configurations of the TiZrNbHf and (TiZrNbHf)98Ni2 alloy are listed in Supplementary Data 1 and 2, respectively. Energy calculations and structure optimization were performed using the Vienna ab initio simulation package40 (VASP) with a plane wave cutoff energy of 320 eV. Only a Γ-centered Gamma k-mesh was used for all configurations to delineate the density of reciprocal space. Projector augmented wave potentials (PAW) were adopted with the Perdew–Burke–Ernzerhof generalized-gradient approximation41 (PBE) for the exchange-correlation functional. To capture the segregation tendency of Ni atoms towards GB region, the segregation energy Eseg was calculated42:

$${E}_{{seg}}=\left({E}_{{GB}}^{{Ni}}-{E}_{{GB}}\right)-\left({E}_{{bulk}}^{{Ni}}-{E}_{{bulk}}\right)$$
(1)

Here,\(\,{E}_{{GB}}^{{Ni}}\) and \({E}_{{GB}}\) are the total energies of the simulated GB model with and without Ni atoms, respectively. \({E}_{{bulk}}^{{Ni}}\) and Ebulk denote the total energies of the corresponding bulk model with and without Ni atoms, respectively. Note that a negative Eseg indicates that the Ni segregation at GB is energetically favorable.

Theoretical prediction of solid solution strengthening

For an alloy containing n types of alloying components with concentrations, the shear yield stress for bcc lattice at zero-temperature can be estimated using Curtin’s solid-solution strengthening model as43

$${\tau }_{y0}=0.04{0{{\rm{\alpha }}}}^{-\tfrac{1}{3}}G\,{\left(\frac{1+v}{1-v}\right)}^{\tfrac{4}{3}}{\left[\frac{{\sum }_{n}\,{c}_{n}\Delta {V}_{n}^{2}}{{b}^{6}}\right]}^{\tfrac{2}{3}}$$
(2)

where G, v, b denotes the shear modulus, Poisson’s ratio and Burgers vector, respectively. The values of G, v, and lattice constant (a) are listed in Table 1. α describes the dislocation line tension, with α = 1/12 for bcc CCAs. TiZrHfNb and (TiZrNbHf)98Ni2 alloys were investigated by DFT calculation and each sample contained 432 atoms (The atom configurations are presented in Supplementary Data 1 and 2). Energy calculation was performed with a plane wave cutoff energy of 350 eV and Brillouin zone integrations of Monkhorst–Pack meshes using a single k-point (Γ). Projector augmented wave potentials were adopted with the Perdew–Burke–Ernzerhof generalized-gradient approximation for the exchange-correlation functional. For each sample, the atomic misfit volume, ∆Vn, for the type-n element, can be determined43

$$\Delta {V}_{n}={\sum}_{m} \, {c}_{m}\left\langle \Delta {V}^{n/m}\right\rangle$$
(3)

where 〈∆Vn/m〉 is the volume change caused by substituting type-m atom with type-n atom (see Table 2) and cm is the concentration of type-m element. Their polycrystalline elastic constants were calculated by combining the stress-strain method44 and the Voigt-Reuss-Hill (VRH) averaging approximation45.

Table 1 Input parameters to the Curtin’s solid-solution strengthening model
Full size table
Table 2 Comparison of atomic misfit volume, ∆Vn, between (TiZrHfNb)98Ni2 and TiZrHfNb alloys
Full size table

Structural and compositional characterization

TEM investigation was performed using a JEM 2200 F FEG transmission electron microscope operated at 200 kV. STEM characterization was conducted in an aberration-corrected STEM/TEM (FEI Titan Themis) at an acceleration voltage of 300 kV. HAADF-STEM imaging was collected with a probe semi-convergence angle of 17 mrad, and the inner and outer semi-collection angles of the annular detector was from 73 to 350 mrad. The chemical information of the alloys was characterized using APT (CAMECA LEAP 5000XR) at 60 K in laser mode, with a pulse energy of 20 pJ, and pulse rate of 200 kHz. The results were analyzed using Imago Visualization and Analysis Software (IVAS 3.8.8). The thin foils for TEM/STEM investigation and the needle shaped samples for APT and correlative APT-TEM characterizations were prepared using a focused ion beam (FIB, FEI Helios Nanolab 600i) workstation. The final parameters used for cleaning were 5 kV/41 pA and 2 kV/23 pA.

Mechanical characterization

Micropillar compression experiments were performed at ambient temperature using a nanoindenter (Hysitron TI950) equipped with a 10 μm-diameter diamond punch, under displacement-control mode and at a nominal strain rate of 5 × 10−3 s−1. Each test was repeated for at least three times. We conducted in-situ SEM bending experiments at ambient temperature using a PI 88 PicoIndenter (Hysitron Inc.) with a tungsten carbide wedge, under displacement-control mode and at a displacement rate of 5 nm/s. The in-situ SEM bending experiments for the evaluation of fracture toughness were performed using a PI85 PicoIndenter (Hysitron Inc.) with a diamond tip, under displacement-control mode and at a displacement rate of 5 nm/s. The loading direction in respective to the columnar grains were schematically depicted in Supplementary Fig. 15. At least three samples were tested at each condition to ensure repeatability. In-situ TEM tension tests were conducted using a Gatan model 654 single-tilt straining holder at ambient temperature in an image-corrected STEM/TEM (FEI Titan Themis) operated at 300 kV.

The thin foils for in-situ TEM tension, micropillars for compression, and microcantilevers for in-situ SEM bending were prepared using a FIB workstation (FEI Helios Nanolab 600i). The micropillars adopt dimensions of 1 μm-diameter, 2 μm-height, and their taper angle was carefully controlled to be smaller than 1o. The microcantilevers for bending have a width of 1 μm, a thickness of 1 μm, and a length of 2 μm. The maximum flow stress in bending was calculated according to the equation46 σmax = 6 × \(\frac{F\times l}{w\times {t}^{2}}\), where F is the maximum load measured in bending, l is the distance between the loading position and the fixed end of the cantilever, w is the width and t is the thickness of the cantilever. The pre-notched microcantilevers with length (L0) of ~8.0 μm, width (W) of ~1.8 μm, thickness (B) of ~1.5 μm for fracture toughness evaluation were prepared using FIB. The cantilevers were notched at 2 μm away from the cantilever beam support, with sharp notch tip radius of ~50 nm and notch depth (a) of ~600 nm. We carefully controlled the a/W value to be 0.3, resulting in a dimensionless geometry factor47 f(a/W) of 6.6. The fracture toughness KIC was calculated using the equation: \({K}_{{IC}}=\frac{{F}_{\max }\cdot L}{B\cdot {W}^{\frac{3}{2}}}f(a/W)\), where the maximum load Fmax was taken from the measured load during bending.