Introduction

The emergence of artificial metamaterial has opened new avenues for exploring the unusual electromagnetic, mechanical, optical and thermal properties of the materials1,2,3,4. These artificial structures introduce a paradigm for engineering the materials with designable structural properties and thus enabling functions beyond the reach of existing bulky materials. They feature micron/nanoscale characteristics, which facilitates various applications ranging from hierarchical photonic devices5,6, electromagnetic and acoustic metamaterials7,8, mechanical metamaterials9,10, and thermal energy transfer11.

So far, artificial structures have been primarily fabricated using lithography techniques, including two-photon lithography (TPL)12, electron beam lithography (EBL)13, nanoimprint lithography (NIL)14, capillary force lithography (CFL)15, and traditional three-dimensional (3D) printing16. Generally, TPL has the capability of producing high-resolution structures with feature size down to 200 nm17,18. However, similar to the EBL relying on pixel-by-pixel writing process19, its limited-throughput caused by seriality renders TPL time-consuming to pattern large-area microstructures17,18. Although this challenge can be partially mitigated by the high-throughput NIL and CFL which are particularly suitable for large-area patterning, they either heavily rely on the master imprint mold or lack flexibility in geometric design14,20,21. Alternatively, traditional 3D printing technique can offer great design flexibility, but it suffers from bottlenecks in patterning accuracy and inherent limitations in materials22. Generally, aforementioned lithography techniques either lean on static masks or have relatively low fabrication accuracy. In principle, the preparation of conventional artificial structures with single height gradients is relatively straightforward, whereas multi-height gradients should turn to top-down or bottom-up methods23,24,25,26. Hence, the cost-effective preparation method of hierarchical structures with micron/nanoscale features remains challenging.

Traditionally, the fabrication of hierarchical structures based on static masks adopts multiple lithography processes requiring the successive replacement of different masks, which is sophisticated and challenging due to the difficulties in accurately aligning the patterns on the masks13,27,28,29. Using an aligner reduces the risk of alignment errors, however, it complicates the manufacturing process and increases the associated time and cost30. Although this challenge can be alleviated by employing multiplexed lithography, allowing for production of various multilevel microstructures, the fabrication of the mask remains complicated31. Recently, there has been increasing attention on the temporal and spatial evolution facilitated by electrically stimulated liquid crystal (LC), as highlighted in these studies32,33. Nematic LC (NLC) stands out as a simple and versatile soft material characterized by optical birefringence and ability to assemble into multifarious architectures under the geometric confinement and external stimuli, thus generating dynamic diffraction patterns with designable properties34,35,36,37,38,39,40. Hence, these dynamic patterns are highly promising in photolithography as metamask for preparing structures with micron/nanoscale features onto the photosensitive materials through one-step lithography.

Herein, we report a dynamic photomask for directed lithography, which is driven by diffraction patterns from assembling the electrically stimulated NLC molecules into multifarious architectures. The virtual metamasks are composed of reconfigurable and switchable diffraction patterns of the NLC architectures, which are enriched with information of grayscale and can be used as bridge in lithography. We adopt the Landau-de Gennes’s Q tensor and nonuniform finite difference method to theoretically predict the optical behavior of the NLC architectures under external stimuli. The resultant diffraction patterns, functioning as the metamask, successfully fabricates two-height gradients microstructure on negative photoresist (HN-018) using one-step lithography process, and the obtained microstructure has feature size about 3.2 times smaller than the initial electrode pattern. This also can produce hierarchical microstructure through in-situ manipulation of the working distance and simultaneous exposures. Moreover, the microstructure is transferred onto a silicon wafer through wet etching, yielding structures endowed with distinctive optical and mechanical properties that align with the diffraction patterns. Remarkably, our metamask is independent from incident wavelengths, making it compatible with a broad range of materials for lithography. This approach streamlines the controlled and flexible production of various microstructures, distinguishing itself through its simplicity, cost-effectiveness, and efficiency in manufacturing. The resulting multi-functional microstructures are highly advantageous for a multitude of applications.

Results

Principle of lithography utilizing metamask

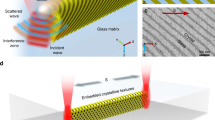
Figure 1 depicts the basic principle of the proposed dynamic photomask directed lithography. Figure 1a and Supplementary Fig. 1 show the schematic setup to create the metamask based on the electrically stimulated assembly NLC molecules into architectures. The continuous-wave laser beam with working wavelength of 405 nm is expanded and subsequently collimated by the beam expander consisting of lens 1, pinhole and lens 2. The collimated beam is converted to circularly polarized light by a linear polarizer (LP) and a quarter waveplate (QWP), and then modulated by the NLC sample, generating coherent diffraction patterns that spatially evolve along the propagation direction (Fig. 1a). The sample of the dynamic NLC photomask is consisted of uniaxial LC material (5CB, with positive dielectric anisotropy) sandwiched between a top glass substrate coated with uniform ITO and a bottom glass substrate with patterned ITO coated with a passivation layer (Hyflon) (Supplementary Fig. 1). Hyflon is an amorphous fluoropolymer, which not only can provide a high resistance as insulating layer, but also can homeotropically anchor the NLC director at the boundary, aligning with the simulation boundary conditions (Supplementary Fig. 2)41. In principle, the optical axis of 5CB molecules undergoes constant fluctuations attributed to thermal movements, and hence only a small amount of energy is sufficient to reorient their directors. This remarkable characteristic allows for manipulating the NLC molecules with an external electric field. The LC director distributions (LC thickness H: 50 μm, electrode diameter D: 20.11 μm, and the spacing between neighboring electrode patterns L: 19.89 μm) along the z-axis and x-z plane have been calculated in response to the applied electric field (1 kHz, 400 Vpp) (Fig. 1b). We applied a voltage of 400 Vpp to ensure the NLC molecules can be sufficiently stabilized (Supplementary Fig. 3). Wherein, the upper and lower surfaces are set to strong homeotropic anchor, and the x-y boundary is set to periodic boundary conditions. The deflection angle is defined as the angle (θ) between the LC director and x-y plane of the lower electrodes (dashed circle in Fig. 1b). For more elaboration on the calculation process and conditions, the relative work could be conducted42. The NLC molecular directors tend to exhibit uniform state (90°) within the conductive ITO region, due to the uniform electric field distribution across the LC layer in the z-axis direction (green region in Fig. 1b). On the contrary, in the circular aperture region without ITO, the NLC molecular directors θ from 33.23 to 90° are circularly symmetric in the transverse planes along z-axis, and follow the electric field in x-z plane, leading to a controllable phase profile (yellow region in Fig. 1b). The LC molecules with a small deflection angle are distributed close to the boundary between 0 and 2 μm (inset in Fig. 1b). Consequently, when the laser beam passes through this region with specific phase retardation, typical diffraction patterns are generated (Fig. 1a). Large quantity of complex diffraction patterns resulted from the constructive or destructive interference between neighboring patterns, appear in the propagation direction, thus providing a promising platform for photomask. The intensity distribution of one of the diffraction patterns is illustrated by the optical microscope (OM) image (Fig. 1c). When it is employed as meta mask to pattern photosensitive materials (negative photoresist HN-018), the microstructure with 3D surface topography is obtained after one-step standard photolithographic process (Fig. 1d). Alternatively, we can also realize a new microstructure (Fig. 1e) after transferring the pattern in Fig. 1d to a silicon wafer by wet etching, providing a promising technique for microelectromechanical systems (MEMS). Our technique reduces the complexity of the fabrication process by eliminating the need for multiple alignment steps which are necessary in traditional lithography.

Fig. 1: Design concept and principle.
figure 1

a Experimental setup and achieved diffraction patterns of the proposed dynamic photomask when the laser beam passes it. b Top: spatial distribution of calculated nematic liquid crystal (NLC) molecular directors along the z-axis driven by an electric field (1 kHz, 400 Vpp); bottom: distribution map of NLC director’s tilt angle (θ) of x-z plane aligning to the electric field (E). The inset highlighted with green rectangle depicts the enlarged part of x from 5 to 20 μm and z from 0 to 9 μm; the inset highlighted with pink rectangle detailly shows the director of each LC molecule x from 8 to 12 μm and z from 0 to 2 μm; the inset highlighted with black circle defines the tilt angle θ. c Experimentally observed optical microscope (OM) image of diffraction pattern, d corresponding 3D surface topography of the microstructure obtained via one-step lithography, and e transferred microstructure on silicon wafer at z = 2530 μm. Note: LP-linear polarizer, and QWP-quarter waveplate. The sample parameters are given as: D = 20.11 μm, L = 19.89 μm, H = 50 μm, U = 400 Vpp, and λ = 405 nm.

Full size image

Modulation of diffraction patterns

We simulated the optical performance of the NLC architectures under the stimulation of electric field after efficiently calculating the molecular director configuration in Fig. 1b. Typical parameters of a circle electrode pattern are given as follows: diameter of the electrode (D = 20.11 μm), spacing between neighboring electrode patterns (L = 19.89 μm), and thickness of LC layer (H = 50 μm). Here, the measured electrode parameters are obtained from the image of scanning electron microscopy (SEM, Phenom G2 Pro, Resolution: 25 nm). The working wavelength of the incident continuous-wave laser beam is 405 nm. The driving alternating voltage (AC) of square wave is set at a frequency of 1 kHz and 400 peak-to-peak value (Vpp)43,44. The resultant diffraction pattern is composed of light fields propagating through the glass substrate and air, where z defined is as the distance between the upper surface of NLC layer and the acquired OM image. Figure 2a (I) shows the simulated images of diffraction patterns propagating along the z-axis at specific distance: z = 0, 335.0, 1401.0, 3188.0, and 4176.0 μm. The diffraction pattern on the upper surface of LC layer, situated at z = 0 μm, is initially circle-shaped due to the retardation arising from the tilted LC molecules close to the patterned ITO region. As z increases, the diffraction patterns evolve, exhibiting various levels of complexity within the circular aperture. Subsequently, a uniform pattern across the whole area is formed due to the coherent interference between the neighboring patterns, morphing from flower-like shapes at z = 335.0 μm to squares, and ultimately returning to circles. Correspondingly, we experimentally record the OM images of diffraction patterns at z = 85.3, 419.9, 1485.0, 3250.0, and 4194.9 μm, which are consistent with the simulation results (Fig. 2a (II) and Supplementary Fig. 4). We also provide two movies to illustrate the dynamic evolution of diffraction patterns in the simulation and experiment (Supplementary Movies 1 and 2). These movies show that the diffraction patterns repeat themselves along the propagation direction after a regular distance away from the exit plane, following the theory of Talbot effect45. This regular distance is widely known as Talbot length and given by \(Z=2({d}^{2}/{{\it{{\lambda }}}})\), where d is a pitch (\(d=D+L\)) and λ is the incident wavelength. Since the image at \({\it{d}}^{2}/{\it{\lambda}}\) corresponds to a negative image, thus we can simply consider half of the Talbot length as the periodic length (\({Z}_{{{{\rm{T}}}}}={d}^{2}/{{\it{\lambda }}}\)) to avoid the repetition of optical patterns. The simulated and experimental \({Z}_{{{{\rm{T}}}}}\) values are estimated to be 4176.0 and 4194.9 μm, indicating a good match, whereas the theoretical \({Z}_{{{{\rm{T}}}}}\) value is 3950.6 μm based on the assumptions of working wavelength of 405 nm and a pitch of 40 μm. This minor difference between the simulated and experimental values can be attributed to the ideal conditions set in the simulation, where the refractive index of air and glass is ideally set to 1.0000 and 1.5000, respectively. The difference between simulated and theoretical values can be attributed to the lack of consideration for the cell thickness in the calculation. The simulated \({Z}_{{{{\rm{T}}}}}\) value includes the propagation distance between the LC layer and the glass and air. Moreover, it can be observed that \({Z}_{{{{\rm{T}}}}}\) is inversely proportional to the wavelength, implying that the dynamic change of diffraction pattern can be tuned with the wavelength. When the wavelength is 532 nm, \({Z}_{{{{\rm{T}}}}}\) value is shortened by 0.76 times (Fig. 2a (III)). However, the same diffraction patterns can be obtained at z = 0.9, 319.0, 1111.0, 2470.0, and 3210.0 μm. This helps to demonstrate that the sample is broadband, which is a significant advantage of the NLC photomask for lithography, due to the greatly expanding selection range of photosensitive materials. To compare the patterns under different conditions, a dimensionless ratio R applicable throughout the entire study is defined as \(\it z/{Z}_{{{{\rm{T}}}}}\).

Fig. 2: Spatial evolution of diffraction patterns.
figure 2

a Simulated diffraction patterns (I) using incident laser beam with wavelength (λ) of 405 nm and experimentally observed OM images at (II) λ = 405 nm and (III) λ = 532 nm at specific distances (z), when D = 20.11 μm, L = 19.89 μm, and H = 50 μm. The scale bar denotes 20 μm. b Normalized intensity along the selected yellow dashed line in the OM images of experimental diffraction patterns in Supplementary Fig. 6a with D = 29.87 μm, L = 10.13 μm and D = 35.05 μm, L = 5.95 μm, when R = 0.289, H = 50 μm and λ = 405 nm. Each colored box along the x-axis highlights a peak or valley that indicates the presence of one of the microstructures. Each color on the curve represents a height gradient. c Normalized intensity at a representative dashed line in the simulated diffraction pattern with different LC layer thickness (H = 1, 5, 9, 30, 50 μm) when D = 20.11 μm, L = 19.89 μm, λ = 405 nm and R = 0.560. d ZT values as a function of the square pitch d (\(d=D+L\)) at (I) D = 20.58 μm, L = 4.42 μm, (II) D = 20.19 μm, L = 9.81 μm, and (III) D = 29.87 μm, L = 10.13 μm for circle aperture; (IV–IX) d = 40 μm for octagonal, hexagonal, square, and triangular aperture; (VIII) D = 30.12 μm, L = 29.88 μm, and (IX) D = 40.23 μm, L = 39.77 μm for circle aperture when H = 50 μm, λ = 405 nm. Error bars in panel (d) represent the standard deviation from at least three experiments. All voltage is 400 Vpp.

Full size image

The pluralistic morphology of the diffraction pattern can also be modulated by changing the electrode shapes (Supplementary Fig. 5). Moreover, it is very reasonable to infer that the diffraction pattern can also be tuned by the electrode parameters. This is demonstrated by the experiments in Supplementary Fig. 6a, where two samples (D = 29.87 μm, L = 10.13 μm and D = 35.05 μm, L = 5.95 μm) with the same pitch but different L and D are fabricated and optically characterized. In order to better illustrate the properties of diffraction patterns, we plotted the normalized intensity of gray value on a representative line. The intensity in the selected yellow dashed line in the OM images (Supplementary Fig. 6a) reveals that the diffraction patterns contain four gray levels, four peaks and valleys when D = 29.87 μm and L = 10.13 μm (Fig. 2b). The gray levels represent the gradients, whereas the peak or valley along the x-axis reflects an indicator of microstructure. However, the features increase to five and six when D = 35.05 μm and L = 5.95 μm. This is because the small deflection angle (28.20°) of the electrically stimulated NLC molecules can lead to maximum refraction of light (Supplementary Fig. 6b), resulting in an increase of interference intensity between the neighbored electrode patterns when D = 35.05 μm and L = 4.95 μm. Compared to the case of D = 29.87 μm and L = 10.13 μm with a minimum angle of 30.49°, the thickness of the electrically stimulated NLC molecules is also increasing, which plays a synergistic role in the complexity of diffraction patterns (Supplementary Fig. 6b). Therefore, it is also imperative to delve into exploring how LC layer thickness affects the gray levels of diffraction patterns when D and L remain unchanged. As aforementioned in Fig. 1b, the orientations of the NLC molecules experience sufficient perturbations when the LC thickness falls below 9 µm when D = 20.11 μm and L = 19.89 μm. The normalized intensity (Fig. 2c) along the designated black dashed line in the simulated diffraction pattern (Supplementary Fig. 7a), showcases discernible variations corresponding to different LC layer thickness (H = 1, 5, 9, 30, 50 μm). At a thickness of 1 μm, the intensity remains a fixed value out of nuanced gradients of gray levels. However, three distinct gray levels emerge with a relatively low contrast at a LC thickness of 5 μm. When the LC thickness is beyond 9 μm, the diffraction pattern characterized by pronounced contrast remains virtually unaltered. This phenomenon can be attributed to the vertical alignment of NLC molecules near the upper electrode, and thus there is an absence of birefringence, leading to negligible impact on the diffraction pattern. Moreover, owing to the small extinction coefficient of 5CB46, the transmitted light intensity exhibits remarkable stability even the LC thickness reaching 50 µm. Simultaneously, these experimentally captured diffraction patterns adopt consistently aligned when H = 30, 50, 80, and 100 μm (Supplementary Fig. 7b). Moreover, we also investigate the other electrode parameter and find that the diffraction patterns are highly adjustable (Supplementary Fig. 8).

Although these diffraction patterns are reconfigurable, they are periodic and follow the Talbot length. Figure 2d shows the corresponding \({Z}_{{{{\rm{T}}}}}\) values as a function of the square pitch d. A linear correlation of \({Z}_{{{{\rm{T}}}}}=2.47{d}^{2}+190.79\) (R2 = 0.99) can be observed in the range of 25 − 80 μm. Similarly, the \({Z}_{{{{\rm{T}}}}}\) values match excellently with the same pitch of 40 μm when the electrode shapes are circular, octagonal, hexagonal, square, and triangular apertures in the red dashed line of Fig. 2d. Supplementary Fig. 7c also shows the \({Z}_{{{{\rm{T}}}}}\) values remain nearly constant at different LC layer thickness, with the slight discrepancies attributed to the variations in LC layer thickness. The cyclic periodicity of the diffraction pattern in the direction of light propagation allows for greatly selecting metamask for photolithography.

Fabrication of microstructure

The efficiency of lithography and stability of photomask are two crucial factors in practical application. In this work, the applied electric field requires certain relaxation time to trigger the rotation of NLC molecules towards the state of minimum total free energy. The measured native response on-time is 477 ms following the case with 400 Vpp (Fig. 3a). Subsequently, upon deactivating the electric field, the NLC molecules revert to their original state within a time-frame of 480 ms. This response time is at least four orders of magnitude smaller than the entire lithography process, proving that our proposal is efficient enough for lithography. Furthermore, the OM images in Fig. 3a affirm that the transitions between stable configurations are entirely reversible, maintaining ultrahigh stability even after 100 switching cycles. Hence, the assembled NLC architectures, functioning as a photomask generator, have the advantages of fast response, excellent stability, and outstanding repeatability, rendering them exceptionally well-suited for the fabrication of microstructure for active applications.

Fig. 3: Fabrication of multi-height gradients microstructure.
figure 3

a Response time (produced via 100 switching cycles) and OM images between on and off state at z = 150 μm. Scale bar: 10 μm. Diffraction patterns of b simulation at z = 1060 μm and c experiment at z = 1078 μm, and the corresponding d 2D profile image and e 3D surface topography of the fabricated height gradient microstructures through one-step lithograph. f Normalized intensity along the representative dashed line in (c) and (e). The experimental parameters are given as follows: D = 20.11 μm, L = 19.89 μm, H = 50 μm, U = 400 Vpp, and λ = 405 nm.

Full size image

In our strategy, the diffraction patterns formed by NLC architectures contain gray information, which can serve as gray mask to pattern the multi-height gradient microstructure. Although microstructures featuring multi-height gradients have been widely utilized in fields such as optics and surface engineering3,47, efficient fabrication remains a challenge. Here, we prove the feasibility of using this gray mask to prepare a typical multi-height gradient microstructure through one-step lithography. We choose the diffraction pattern of sample with circular electrode array (d = 40 μm, H = 50 μm) at position of 1060 μm (Fig. 3b). The normalized intensity of the dashed line in the simulated diffraction pattern exhibits a minimum 6 gray levels (Supplementary Fig. 9). Each peak or valley along the x-axis reflects an indicator of lithographic resolution, with simulation results suggesting an achievable resolution of 1.2 μm. Compared to the state of art spatial light modulators (SLMs) with minimum resolution is 3.74 μm, our result is a significant breakthrough48,49. After using this diffraction pattern (Fig. 3c) as a metamask for lithography, the diffraction pattern is successfully replicated onto the negative HN-018 photoresist coated on the glass by one-step lithography, which can be partially demonstrated by the 2D profile image of microstructure (Fig. 3d). The resulting 3D surface topography image displays at least two-height gradients on photosensitive materials with an 8 μm thickness (Fig. 3e). The 1st gradient microstructure corresponds to the glass substrate, as evidenced by the region with null diffraction light. The average size measures 6.2 μm, which is 3.2 times smaller than the designed electrode size, as shown in the red dotted box in Fig. 3e. The 2nd gradient microstructure displays a thickness ranging between 4 and 6 μm, while the 3rd gradient manifests a thickness of approximately 8 μm, aligning with the initial thickness of the photoresist layer. Figure 3f plots the normalized intensity and height of the selected dashed line containing 3 levels on the image of Fig. 3c, e. The 2nd level has subtle difference within a range, attributing to the low accuracy of laser. This approach for fabricating multi-height gradient microstructures through one-step lithography is time-saving and cost-effective. Meanwhile, this method provides a balanced solution with adequate resolution and significantly higher throughput compared to two-photon lithography, making it much practical for manufacturing large-area pattern17,18.

Owing to the high freedom of this photomask, hierarchical microstructures could also be easily generated in-situ using the one-step multilayer photolithography technique. Specifically, the sample undergoes exposure to the first target light field and then to the second light field at another longitudinal location, both originating from the same photomask (Fig. 4a). Through this process, the two light fields are superimposed and embedded together into the same sample, hence the hierarchical microstructure can be realized through rather simple lithography process. Theoretically, holographic image through incorporation of multiple into the same hierarchical 3D microstructure can be achieved by multi-exposing process (Fig. 4a). As a proof of concept, we experimentally fabricate a hierarchical microstructure by superimposing two metamask, namely two diffraction patterns (Fig. 4b). The sample of HN-018 photoresist coated on glass is initially exposed at z = 3400 μm and then mechanically moved to 4100 μm for the second exposure. Ultimately, three levels microstructure is achieved after developing. The 3D surface topography image of resultant hierarchical microstructure shows that the 1st level microstructure corresponds to the glass substrate, the 2nd level microstructure is formed by the first exposure, and the 3rd level microstructure emerges from the combining effects of the two exposures, resulting in the highest gradient (Fig. 4c). It should be emphasized that the dynamic photomask for lithography facilitates the creation of hierarchical microstructures in a novel manner, avoiding alignment errors that may arise in multiple lithography compared to EBL13.

Fig. 4: Fabrication of hierarchical microstructure.
figure 4

a Schematic diagram of hierarchical microstructures and holographic image preparation. b Experimentally observed OM images and corresponding to the light intensity of diffraction patterns at z = 3400 and 4100 μm. c 3D surface topographies of resultant hierarchical microstructures from two exposures. The experimental parameters are given as follows: D = 20.11 μm, L = 19.89 μm, H = 50 μm, U = 400 Vpp, and λ = 405 nm.

Full size image

Naturally, the realization of single-layer microstructure on the photosensitive material (HN-018) photoresist coated on the silicon wafer is possible through using our metamask (Fig. 5a). The recorded 3D surface topography image after lithography aligns closely with the OM image (Fig. 5b). Subsequently, leveraging the derived 3D surface topography of microstructure, the mechanical performance of the obtained material is calculated under the 5×108 N/m2 stress using the open-source COMSOL software (Fig. 5b). It is found that the microstructure is anisotropic and possesses a period of 180°. Such kind of anisotropic microstructural materials plays a key role in areas such as the human brain or tendons10. Apart from the demonstration of producing anisotropic microstructure, we transfer the resultant microstructures from the photosensitive material to the silicon wafer by a wet etching process (12.5 wt% TMAH, 300 rpm, 80 °C, 5 min). The scanning electron microscopy (SEM) image of the produced microstructure (Fig. 5c) illustrates that there is bowl-like structure from a similar square master microstructure, characterized by numerous random upright pyramids (UPs) on the surface. In contrast, the numbers of UPs on the surface decrease in case without microstructure under the same experiment condition (Supplementary Fig. 10). It has been already proven that these textured surfaces which are covered by UPs are promising for manufacturing high-efficiency silicon solar cells50,51. The reflectance spectrum of Fig. 5d, e shows that when the standard silicon wafer is used as a baseline and its performance is set to 100% for comparison, the overall averaged reflectance of the textured surfaces covered with UPs but without trapping of microstructure is 60%. In contrast, the overall average reflectance can be reduced to 19% due to the trapping effects of microstructures arising from the multiple reflection that maximizes the absorption of the incident light. It implies that these microstructures can be transferred onto the silicon wafer, holding the promise in high-efficiency solar energy harvesting.

Fig. 5: Optical and mechanical properties of microstructures.
figure 5

a Experimentally observed OM image of diffraction pattern, corresponding b 3D surface topography of microstructures obtained via the lithography: (top) the 3D data model from 3D surface topography and (bottom) the simulated mechanical response of the microstructure at different angles at a specific distance (z = 3400 μm). c Top view of SEM image of upright pyramids (UPs)-textured silicon wafer obtained by etching in (b). d Schematic diagram of sunlight reflection on UPs-textured silicon wafer. e Reflectance spectrum of standard silicon wafer, and UPs-textured silicon wafer without and with trapping effects of microstructures responding to sunlight. The experimental parameters are D = 20.11 μm, L = 19.89 μm, H = 50 μm, U = 400 Vpp, and λ = 405 nm.

Full size image

Discussion

We have developed a cost-saving methodology of harnessing electrically driven NLC assembly architectures to craft a dynamic photomask. Our study demonstrates that modulating the spatially localized orientations of the NLC molecules enables the tuning of the wavefront of the incident laser beam, and consequently leads to intricate diffraction patterns. These patterns can achieve a resolution of 1.2 μm, in compared to the state of art SLMs with a resolution of 3.74 μm, significantly enhanced resolution in lithography applications. Meanwhile, these diffraction patterns are enriched with grayscale information, which may function as metamask and serve as powerful catalysts for lithography. We have successfully prepared the multi-height gradients microstructure onto photosensitive materials (HN-018) by using the proposed metamask. Furthermore, based on the high freedom of the photomask in the propagation direction owing to the coherence between neighboring electrode patterns, we obtain a kind of hierarchical microstructures through in-situ modulation of work distance from sample photomask. In comparison with the traditional multilayered photolithography methods for fabricating hierarchical microstructures, our proposal eliminates intermediate alignment steps and significantly enhances the efficiency. Remarkably, the microstructure can be transferred onto silicon wafer, and the ensuing microstructures featuring random upright pyramid shapes showcase good optical performance, expanding the application of this methodology. However, we noticed in the experiments that the resolution and height gradient of the obtained microstructures deviated from perfection in comparison to the simulation. Envision an enhancement in this work, enhancing the uniformity and power output of the laser, reducing the pattern size, or using high-power ultraviolet laser will lead to better precision, more height gradients and even nanoscale structures. Furthermore, the established simulation method serves as a valuable predictive tool, successfully forecasting a spectrum of diffraction patterns. Looking forward, our vision encompasses the capability to create arbitrary multilevel structures even holographic image through the pre-superimposition of meticulously designed patterns. These strides open expansive application possibilities for customizable metamaterials across various fields such as mechanics, optics, photonics, electronics and so on.

Methods

Experimental design of photomask

We fabricated the electrode arrays using a standard lithography process. Initially, the ITO substrate was cleaned with a 4 wt% alkaline solution, followed by rinsing with DI water and drying with nitrogen blowing. A positive-type photoresist (SUN-120P) was spin-coated onto ITO substrate (step 1: 500 rpm for 5 s; step 2: 3000 rpm for 60 s) and then soft-baked at 120 °C for 90 s on the hot plate (EH20B, Lab Tech, Beijing, China). UV light exposure (13 mW·cm−2 for 13 s) was performed using an aligner (URE-2000/35, Institute of Optics and Electronics, Chengdu, China) with a chrome mask with designed patterns, and then the substrates were submerged in a developer (0.5 wt% KOH) for 90 s. Afterwards, it was cleaned with DI water and blow dried with nitrogen. The patterned photoresist was then hard-baked on the hot plate at 120 °C for 30 min. The substrates were then submerged in an acidic etchant (37 wt% HCl: 68 wt% HNO3: H2O = 50: 3: 50, V/V) until the exposed ITO area was fully etched. The photoresist residue was removed by ethanol after cleaned by DI water and then dried by nitrogen blow to obtain the patterned electrode.

The LC materials were assembled between two glass substrates (Supplementary Fig. 1). First, the bare and patterned ITO electrode was spin-coated with Hyflon (377 nm) to form a stable dielectric protective layer. The upper substrate was made of a Hyflon-coated uniform ITO electrode. The lower substrate was patterned electrode with Hyflon. The cell was assembled by patterned electrode and a bare ITO electrode using a commercial-available double tape (TESA, German) as a spacer. To easily connect the wires, two substrates were controlled in dislocation. Subsequently, the LC cell was filled with 5CB by capillary force at 40 °C above the isotropic temperature and then cooled down to the room temperature. Additionally, we sealed the edge using the UV curing to prevent the leakage of LC.

Schematic diagram of optical path

Supplementary Fig. 1 depicts the experimental platform used to optically characterize the samples. A collimated Gaussian beam is expanded by the beam expander consisting of lens 1, pinhole, and lens 2. After that, it is converted into circularly polarized light by a linear polarizer (LP) and a quarter waveplate (QWP). Finally, the collimated beam, reflected by a mirror, normally impinges onto the sample placed on the microscope stage. Charge Coupled Device (CCD, Leica DMC 4500) together with a ×5 magnification objective lens is used to collect the diffraction field of the sample. The blue double arrow represents the moving direction of the stage, and the distance between the upper surface of NLC layer and the acquired OM image is defined as “z” (Supplementary Fig. 1). The diameter and spacing of the patterned electrode are denoted with “D and L” and the pitch is “\(d=D+L\)”. The thickness of LC layer is described as “H”.

Preparation of lithography samples

The microscope cover glass and the silicon wafer were cleaned by soaking them in piranha solution (H2O2: H2SO4 = 1: 3), and rinsed with DI water and blow dried using nitrogen. The HN-018 photoresist was spin-coated on the glass and silicon wafer: step 1: 500 rpm for 5 s, step 2: 1000 rpm for 65 s for 8 μm thickness; step 1: 500 rpm for 5 s, step 2: 2000 rpm for 65 s for 4 μm thickness; and step 1: 500 rpm for 5 s, step 2: 2500 rpm for 65 s for 3 μm thickness. After that, it was soft-baked at 90 °C for 90 s, exposed, developed for 30 s with 0.4 wt% KOH, and then hard-baked at 210 °C for 30 min on a hot plate.

Numerical methods

To simulate the optical properties of the NLC device, the first task is to efficiently calculate the molecular director configuration. According to P. G. de Gennes52, the average molecular direction of rod-shaped uniaxial molecule 5CB can be described by its director n (n = -n). Therefore, the Landau-de Gennes’s Q tensor is employed to represent the director’s configuration and the elastic free energy of NLC. Afterwards, the NLC molecular directors tend to rotate to reduce the overall energy of the system and ultimately rearrange along the electric field based on the dielectric anisotropy when a voltage is applied. The total free energy is minimized when the energy of the electric field is competitive with the elastic energy of NLC. The Euler-Lagrange equations are used to solve the director configuration by using the relaxation method based on dynamics53. To expedite the calculation process, techniques such as the momentum gradient descent algorithm, the improved successive over-relaxation method, the multigrid, and the symmetric boundary conditions are utilized. The formulas of calculation processes refer to the Supplementary information.

After obtaining the director configuration of NLC molecules between the sandwich electrodes, this information is used to model the device and then simulate the diffraction field using the commercial-available FDTD (Finite-Difference Time-Domain) software. Basically, the model in this study cannot be fully simulated by the FDTD software due to the heavy computational cost. However, we notice that the light passing through the NLC layer propagates through a uniform and parallel medium of glass and air. In this case, the diffraction pattern can be efficiently simulated using the vectorial Rayleigh-Sommerfeld diffraction formula and fast Fourier transform, which help to greatly reduce the computing resources and run time. For more details about the simulation and calculation process, please refer to the work by Guo et al.42.

Materials

Indium-tin-oxide (ITO) coated glass (700 μm, 90 ± 10 Ω·sq−1, Leaguer Optronics CO., Ltd, Shenzhen, China) was employed as electrode substrates. The 110 μm thickness microscope cover glass (Fisherbrand®) was procured by Thermo Fisher Scientific, Germany. P-type (100) 4″ silicon wafers were acquired from Lijing Optoelctronics Co., Ltd. (Suzhou, China). Nematic liquid crystal 4-cyano-4’-pentyl-biphenyl (5CB, TNI = 35 °C; K11 = 6.2, K22 = 3.9, K33 = 8.2 pN; ε‖ = 18.5, ε⊥ = 7.0; ne = 1.6975, no = 1.5350) was purchased from J&K Scientific Co., Ltd., China. Hyflon (AD 40 SX 2.5 wt%) was obtained from Solvay (Shanghai) Co., Ltd., China. Negative-type photoresist (HN-018) and positive-type photoresist (SUN-120P) was soured from Suntific Microelectronic Materials Co. Ltd, Weifang, China. KOH and TMAH (Tetramethylammonium hydroxide) were purchased from Aladdin, Shanghai, China. H2O2, H2SO4, HCl and HNO3 was obtained from Guangzhou chemical reagent Co., Ltd., Guangzhou, China.