Introduction

An intriguing benefit of molecular electronics involves the high degree of freedom in synthesizing molecular structures as nanometer-sized electrical components1,2,3. In order to be used in applications, their fundamental charge transport mechanisms have to be understood. A key phenomenon is quantum interference4,5, owing to the wave-like nature of an electron traversing the molecular nanostructure. Despite being a quantum mechanical effect, this mechanism leads – even at room temperature – to large (up to more than an order of magnitude) variations of the conductance.

Different external stimuli have been used to control quantum interference, including electrical/electrochemical gating6,7,8,9, mechanical manipulation10,11,12,13,14,15 and the combination of both16. However, to establish a clear connection between experiments and theoretical predictions a full reconstruction of the interference features is highly desirable. Preliminary attempts to reconstruct such features from experimental data were performed by electrochemical gating, i.e., as a function of energy7,8. At cryogenic temperatures, a three-terminal graphene device was used to map the transmission as a function of gate voltage and to quantify the enhancement of transistor performance by quantum interference9. In addition, thermoelectric measurements can provide crucial information concerning charge transmission through molecular junctions17; in the context of measurements across destructive quantum interference conductance dips, single-molecule thermopower experiments have so far not been reported.

Instead of employing electrostatic gating we here use mechanical manipulation to reconstruct the destructive quantum interference feature of a tailor-made para-connected naphthalenophane, whose global (thermo)electrical transport properties have been reported in ref. 18. Like other similar structures with π-stacked moieties11,12,13,19 this molecule is expected to exhibit mechanically induced destructive quantum interference features. With a distance modulation technique11,20 we employ this mechanosensitivity to reconstruct the quantum interference feature as a function of electrode displacement with two complementary break-junction techniques: (i) the mechanically controlled break-junction (MCBJ) technique, to take advantage of its high mechanical stability allowing for the accumulation of large amounts of data and robust statistical analysis, and (ii) a novel alternating current scanning tunneling microscope break-junction (AC-STM-BJ) technique, to realize the continuous simultaneous measurement of both conductance G and thermopower S. The conductance data is used to determine in each cycle of the modulation the electrode displacement of the molecular configuration, for which the conductance minimum of the interference dip occurs. Profiting from the interference dip as reference point of the individual measurements allows for the first time the comparison of different configurations and the analysis of the thermopower while traversing the quantum interference dip. Detailed atomistic modeling employing density functional theory (DFT) calculations and molecular dynamics (MD) simulations demonstrate the crucial role that thermal fluctuations at room temperature play in both single-molecule conductance and thermopower experiments.

Results and discussion

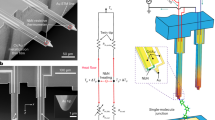
In the wake of previously studied compounds11,12, we analyze the intrinsic mechanosensitivity in the electrical response for para-connected naphthalenophane para-NP as displayed in Fig. 1a; its basic (thermo)electrical characterization has been reported in a previous study18. To explore the role of quantum interference, distance modulation experiments have been performed under ambient conditions in a home-built MCBJ set-up21. A schematic of the set-up is depicted in Fig. 1b. The technique entails a lithographically defined gold nanowire on a flexible substrate, which is bent and ultimately broken using a three-point bending mechanism driven by a piezo-electric element. Molecules are introduced by dropcasting a molecular solution of 5 μM of the acetyl-masked derivative in dichloromethane (DCM) directly onto the sample. At room temperature the molecules hydrolyze at the electrode surface and a covalent S-Au bond is formed. The stability of the latter is crucial to enable the mechanical manipulation of the molecule’s structure. Modulation experiments are performed at ambient conditions and entail the periodic manipulation of the piezo-voltage, thereby periodically modulating the lateral electrode displacement. During these experiments, the current across the junction is measured with a bias voltage of 100 mV (see Fig. 1c). The technique allows for acquiring large data sets (up to 10,000 consecutive traces) and corresponding statistics (see the supplementary information (SI) for further details).

Fig. 1: Modulation experiments on a para-connected naphthalenophane (para-NP) using the mechanically controlled break-junction (MCBJ) technique.
figure 1

a Acetyl-protected form of the para-connected naphthalenophane, para-NP. b MCBJ set-up. c Modulation experiment using the MCBJ. Top panel: triangular wave (orange) applied to the piezo-electric element, connected to the pushing rod, resulting in a modulated distance between the electrodes of 0.3 nm. Center and bottom panels: different types of conductance response of the molecular junction on the electrode distance modulation. Center panel: in-phase (red) and anti-phase (light blue) conductance response. Bottom panel: double-frequency conductance response (blue). d Reconstruction of the quantum interference dip using data from the bottom panel in (c): individual dips (blue) and their average (black).

Full size image

Analogous to previously measured mechanosensitive paracyclophane structures11,12, three kinds of conductance response of the para-NP to mechanical modulation of the electrodes occur as shown in Fig. 1c. They originate from different molecular configurations at the beginning of the modulation. The center panel displays both the anti-phase response, in which the junction conductance decreases as the electrode separation increases, and the in-phase response, in which the conductance increases as the electrode separation distance increases. Note, that the anti-phase and in-phase behavior correspond to pre-compressed and pre-stretched configurations of the molecular junction, respectively. Finally, the bottom panel depicts an example of the double-frequency response, which occurs at a near-equilibrium configuration of the molecular junction. In this case the destructive quantum interference dip is traversed during both the increase and decrease of the electrode separation distance, leading to the observed frequency doubling11,12.

The double-frequency response is the main subject of this study as we will use it to reconstruct the destructive quantum interference dip as shown in Fig. 1d. The conductance vs. time data at the bottom panel of Fig. 1c is the starting point for this reconstruction: To get from Fig. 1c to d we first split the full trace into individual parts consisting of single dips and represent them as a function of electrode distance. By taking the dips corresponding to retraction of the electrodes as the reference, the ones corresponding to the approach are mirrored and placed on top of them. The conductance minima are taken as the zero displacement, i.e., as the point at which the destructive quantum interference dip is at its zenith. Finally, the average of conductance values at a given displacement range is calculated and superimposed as the black trace in Fig. 1d on top of the individual conductance traces. A more thorough description can be found in the SI.

The aforementioned method profits from the excellent mechanical stability of the junctions in MCBJ experiments. The maximum modulation time is set to 15 s and traces that show a response above the noise floor for a duration of at least 2 s are denoted as molecular traces, as junctions in which no molecule is trapped typically reach the noise floor due to self breaking faster. Traces, where the molecular response shows the double frequency behavior consecutively for at least 2 s, are then used for the dip reconstruction. The example shown in Fig. 1c originates from a data set of in total 9,956 consecutive traces, where we observe 2,465 molecular traces of which 192 show the double frequency behavior. In the SI five other examples of dip reconstruction are shown from this dataset, alongside five other examples from another data set containing 10,000 traces. Also in the SI, a collection of 50 dips (25 of each data set) can be found alongside a histogram containing the values of the corresponding dip minima. On average, we find a difference of half an order of magnitude in conductance values for a displacement change of 0.2 nm. The exact shape of the reconstructed dip varies from trace to trace, while the conductance minimum ranges from 10−6G0 to 10−4G0. Here, G0 = 2e2/h is the quantum of conductance with e the elementary charge and h the Planck constant.

Having established the modulation experiments as a robust technique to reconstruct the destructive quantum interference dip in conductance vs. electrode displacement, we now introduce the AC-STM-BJ set-up. While being mechanically less stable than the MCBJ, implementing this technique allows for mapping simultaneously and continuously the conductance and thermopower of the junction as a function of the electrode displacement without the need to stop the electrode movement as in previous techniques22. A schematic of the set-up is shown in Fig. 2a. While a surface resistor is employed as a heater to establish a temperature difference between the gold tip (Th) and the sample (Tc), an AC bias is applied to the tip. Using multi-frequency detection, the DC component of the thermocurrent generated at the junction is continuously measured, thereby allowing the extraction of the Seebeck coefficient at ambient temperatures. Further details can be found in the SI.

Modulation experiments have been performed in a similar fashion as with the MCBJ technique, discussed above. A voltage modulation is applied to the piezoelectric tube connected to the STM tip, while the substrate remains fixed. Molecules are introduced by immersing a pre-annealed Au(111) substrate into a 1 mM molecular solution in DCM for 20 min., after which the substrate is blown with helium gas and loaded into the set-up. Figure 2b displays results of the double-frequency feature from the simultaneous conductance and thermopower measurements. The center panel depicts the double-frequency conductance behavior of the molecular junction, unveiling its destructive quantum interference feature. The bottom panel shows the corresponding thermopower, i.e., the Seebeck coefficient measured with an applied thermal gradient of 38 K. In Fig. 2b, the conductance range at which the double frequency oscillations occur is located between 10−4G0 and 10−3G0, values that are on the high side but consistent with the observations in the MCBJ. Seebeck coefficients are in the range of 10 μV/K to 20 μV/K, similar to the average value of 10 μV/K reported earlier in fast-breaking experiments with the STM-BJ technique18.

Fig. 2: Modulation experiments on para-NP using the alternating current scanning tunneling microscopy break-junction (AC-STM-BJ) technique.
figure 2

a AC-STM-BJ set-up, in which substrate-tip distance modulation experiments of conductance and thermopower response are recorded simultaneously. b Results from modulation experiments using the AC-STM-BJ. Top panel: 3.5 Hz triangular voltage wave with a peak-to-peak amplitude of 15 mV applied to the piezo-electric element (orange), connected to the STM tip, resulting in a tip-substrate modulation distance of 0.3 nm peak-to-peak. Center panel: double frequency conductance response of the molecular junction (blue). Bottom panel: corresponding thermopower signal with Th−Tc = 38 K (red). c Superimposed individual conductance dips obtained from multiple modulation experiments, where the molecular junction exhibits double frequency conductance response (blue) and their calculated average (black). d Corresponding thermopower response (red) and its average (black).

Full size image

In the same way as the analysis performed for the MCBJ experiments, double frequency conductance behavior can be used to reconstruct the quantum interference dip as illustrated in Fig. 2c. The dip minimum is located around 10−4G0, while for negative displacements of 0.2 nm a conductance increase of almost one order of magnitude is observed. Knowing the position of the dip minimum, the corresponding thermopower evolution for displacements across the interference dip can now be deduced from the data (see Fig. 2d and the SI for more details). The Seebeck value of the average curve starts around 14 μV/K for negative displacements and increases to 18 μV/K at the positive side, after passing a minimum of 10  μV/K. Comparing the average conductance and the corresponding thermopower, while going from negative to positive displacement, a decrease for both is observed until a minimum in the thermopower is reached. The minimum in conductance appears later, after which both the conductance and thermopower increase. We note that the sign of the Seebeck coefficient does not change while crossing the destructive quantum interference dip.

Other examples of simultaneous measurements of the conductance and corresponding Seebeck response can be found in the SI, showing a very similar behavior. Herein, the minimum of the reconstructed dips can be found between 10−5G0 and 10−3G0, overlapping in range with the dip minima found for the MCBJ approach. Besides experiments on the para-NP, simultaneous measurements of a meta-NP have been performed, for which the molecular junctions show no double-frequency behavior (see the SI).

To understand the quantum transport properties of para-NP single-molecule junctions, we model electronic transport as phase-coherent and elastic in terms of the Landauer-Büttiker scattering theory23. The electronic transmission τ(E) is determined by combining DFT calculations with nonequilibrium Green’s function (NEGF) methods24. From the transmission, both the conductance G and the thermopower S are derived in linear response theory. Since DFT calculations have known shortcomings in terms of the underestimation of the gap between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO), and the energy alignment of molecular and metallic states at surfaces25,26, we use the DFT+Σ correction26,27. As discussed in detail in the SI, the correction comprises a molecular and an image-charge term.

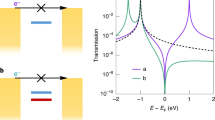
Figure 3a shows the calculated transmission as a function of electrode displacement and energy. Resonances of HOMO levels lie between energies of  −7.0 and  −6.0 eV, those of LUMO levels between  −2.0 and  −1.0 eV. Controlled by mechanical manipulation a destructive quantum interference crosses the entire HOMO-LUMO gap, making it a robust feature and leading to a strongly suppressed transmission around zero electrode displacement. The destructive quantum interference enters the gap at the intercept of HOMO levels at around  −0.025 nm, traverses the gap and passes through the crossing of LUMO levels at around 0.075 nm. Above displacements d of 0.075 nm and below  −0.025 nm the symmetry conditions for a destructive quantum interference are not met12,28, and frontier orbitals interfere constructively (for a discussion of orbital symmetries see the SI).

Fig. 3: Transport calculations for para-NP single-molecule junctions based on the DFT+Σ approach.
figure 3

a Transmission as a function of electrode displacement d and energy E. b Thermopower as a function of electrode displacement and Fermi energy EF at T = 300 K. White areas correspond to values around 30 μV/K or above. The black solid line indicates vanishing thermopower and thus the positions of sign changes. Horizontal dashed lines in panel a mark the range of Fermi energies explored. c Overview of conductance values as a function of electrode displacement, showing the averaged and rescaled experimental data of Fig. 2 and the standard deviation as shaded area, DFT+Σ data using an electronic thermal smearing in the electrodes corresponding to T = 300 K, and DFT+Σ data employing an additional displacement and energy averaging with σd = 0.28 Å and σE = 0.11 eV. In the computations we set EF = −5.3 eV, and each curve is aligned to the displacement d0 with its respective conductance minimum. d Same as in panel c but for the thermopower. The displacement d0 is fixed by the conductance. The inset in the upper left corner shows the extended central cluster used in the quantum transport calculations for d = 0 nm, near the destructive quantum interference dip. The Euclidean sulfur-sulfur distance amounts to 1.15 nm in this configuration. An animation of the stretching process as a function of displacement d is provided as Supplementary Movie 1.

Full size image

Figure 3b illustrates the computed thermopower as a function of electrode displacement and corresponding Fermi energy EF. The experimental work function of gold is in the range of  −5.3 eV and depends on the crystal surface29. Here, we consider an energy range from EF = −5.75 to −4.5 eV. Of particular interest is the thermopower’s sign behavior. Sign changes of the thermopower are expected once a destructive quantum interference feature is crossed5,17,30,31,32,33. In Fig. 3b, we indicate a vanishing thermopower with the black drawn line. The simulations with static junction geometries predict sign changes near the destructive quantum interference for Fermi energies above EF = −5.5 eV, i.e., in the experimentally relevant range.

Direct comparisons between theoretical predictions and experimental data are presented in Fig. 3c for the conductance and in Fig. 3d for the thermopower. Distance modulations in the experiments deform both the elastic gold electrodes and the molecule trapped inside the junction34,35. To relate to the theoretical simulations with rather stiff electrodes, we consider the whole junction of molecule and electrodes as a spring system. From this analysis we determine a scaling factor of 0.57 for the ratio of displacement of the molecule or junction gap size to total experimental electrode displacement. Details of the model are discussed in the SI. Through rescaling, the experimental conductance of Fig. 2c is compressed to a smaller displacement range in Fig. 3c, and thus the experimental destructive quantum interference dip becomes more pronounced and exhibits steeper slopes on both left and right sides towards the minimum. Similarly, the experimentally determined average thermopower and its standard deviation of Fig. 2d are shown in Fig. 3d in the rescaled form.

Comparison between the experimental data for the conductance G and the DFT+Σ results including the electronic thermal broadening in the electrodes shows qualitative similarities, see Fig. 3c. Quantitatively, however, the conductance minimum of the simulation is nearly two orders of magnitude too small, and slopes towards the minimum are much steeper than observed experimentally. Similar conclusions hold for the thermopower in Fig. 3d, where calculations show a sinusoidal form around the destructive quantum interference feature. The minimum of the thermopower of approximately  −2 μV/K on the displacement axis is reached before the minimum of the conductance, both being ~0.01 nm apart. Instead, the experimental data in Fig. 3d exhibits a slight decrease to a minimum of 10 μV/K near d − d0 = −0.03 nm, and a flat maximum at the upper displacement range. Let us stress that a sign change is predicted in the simulation, but is not observed in the experimental data. Electric and thermoelectric transport are thus qualitatively well described by the DFT+Σ method, but significant quantitative deviations from the experimental results remain.

These differences are explainable by thermally induced configurational and energetic fluctuations, which are not captured in the theoretical description using static junction geometries. To include such effects, averaging schemes are proposed in the literature which typically calculate electronic transport properties for a set of junction geometries (e.g. created by MD simulations)36,37,38,39,40,41,42 or perform a statistical average over different molecular configurations43,44. Here, we introduce an averaging scheme to describe the experimental data obtained from a few traces at the destructive quantum interference dip.

The design of the studied para-NP is optimized to avoid torsional modes. The main configurational degree of freedom of the molecule is thus a length variation, when naphthalene decks shift with respect to each other. We hence take configurational effects into account by averaging the simulated transmission data over the displacement axis with a Gaussian distribution. Further energetic variations beyond the image-charge correction of the DFT+Σ model may arise from fluctuations in the electromagnetic environment of a junction. They can cause changes in the Fermi energy in the range of several hundred meV45, which we account for by averaging in Fig. 3a not only over the displacement direction with σd but also over the energy direction with σE. From MD simulations of para-NP junctions we extract a standard deviation of around σd = 0.27 Å at room temperature. A description of MD simulations performed, a sensitivity analysis for the choice of σd, σE and the Fermi energy are provided in the SI. The stability analysis demonstrates that our method is robust across a wide range of parameters. Good agreement between rescaled experimental data and thermally averaged DFT+Σ data in Fig. 3c and d is obtained for σd = 0.28 Å, σE = 0.11 eV and EF = −5.3 eV. It is important to note that σd is very close to the value estimated by MD simulations. Additionally, an upper bound σE  ≤ 0.2 eV is set by the order of minima for conductance and thermopower on the displacement scale. Note that it is a feature in all acquired experimental data that the minimum in the thermopower is reached before the minimum in the conductance. Displacement- and energy-averaged DFT+Σ results at EF = −5.3 eV are shown in Fig. 3c and d. The conductance and thermopower, obtained by the averaging procedure, are within the experimental range. Importantly, the calculated averaged thermopower does not exhibit a sign change.

Thermally driven fluctuations hence smooth destructive quantum interference dips. As single-molecule junction experiments require a statistical analysis, we compare the simulations to additional dip reconstructions in the SI. We find that these combined conductance and thermopower measurements of the dip reconstruction can also be well reproduced with our averaging approach, pointing at the power of the simulation as proxy of the experiment. Furthermore, theory on the related meta-linked naphthalenophane derivative (meta-NP) consistently shows that a destructive quantum interference dip is not detectable through mechanical manipulation, in agreement with experiment (see SI).

From a broader perspective, we expect the presented analysis to hold in molecular junctions which have a sharp feature in the transmission curve, i.e., show a strongly nonlinear dependence of transmission on energy, displacement or both. Thus, even for rigid molecules sharp quantum interference features may be smeared at ambient conditions. Concerning thermoelectric experiments on single molecules at room temperature, our data indicates that one should be careful with the interpretation of the sign of the Seebeck coefficient near narrow dips or peaks in the transmission. High thermoelectric efficiencies have been predicted at destructive quantum interferences due to a large logarithmic energy derivative of the transmission and correspondingly enhanced thermopower46,47. Such effects may be attenuated at ambient conditions due to thermal fluctuations. We further note that the given fluctuations in molecular junction length (0.3 Å) and in energy (0.1 eV) are for gold and molecules with thiol-gold bonds; for molecular systems sharing these properties, the quoted values could be taken to estimate the thermal influence. For other electrode materials and anchoring groups the values may be different.

We developed a statistical analysis to study destructive quantum interference as a continuous function of electrode separation. For this purpose we used the mechanoelectric sensitivity of a para-connected naphthalenophane, para-NP, tailor-made to possess a high conductance and minimal torsional degrees of freedom. Using a modulation technique, we demonstrated consistent results for two experimental approaches, MCBJ and AC-STM-BJ. The MCBJ method was used to reveal the destructive quantum interference effect at different conductance values with a high statistical sampling. The AC-STM-BJ method offers the advantage of continuous and simultaneous conductance and thermopower measurements, and we employed it to correlate conductance and thermopower in the vicinity of the destructive quantum interference. We showed that the thermopower exhibits a sinusoidal shape in this range and that it does not change its sign when the destructive quantum interference minimum of the conductance is crossed. Comparison to theory for static junction geometries shows qualitative agreement with the experimental data. In order to reach quantitative agreement with both the conductance and thermopower data, dynamic effects from fluctuations in geometry and energy are crucial, and at room temperature we quantify junction-length fluctuations and energy variations to be around 0.3 Å and 0.1 eV, respectively.

Methods

Conductance and thermopower measurements using the AC-STM-BJ technique

An AC bias voltage of 15 mV RMS at a frequency of 2.123 kHz is applied to the sample, while the tip is heated by a constant current passing through a surface mount resistor. The resulting current through the molecular junction has AC and DC components proportional to the conductance and thermopower of the junction, respectively. After amplification in a transimpedance amplifier, these components are separated using a Zurich Instruments HF2LI lock-in amplifier, allowing for the simultaneous and continuous determination of the electrical conductance and thermopower. Further details can be found in the SI.

Calculation of transport properties

Conductance G and thermopower S are calculated within linear response theory via23:

$$G={G}_{0}{K}_{0}(\mu,T)\quad \,{\mbox{and}}\,\quad S=-\frac{{K}_{1}(\mu,T)}{eT{K}_{0}(\mu,T)}.$$
(1)

Here, \({K}_{n}(\mu,T)=\int_{-\infty }^{\infty }{{{\rm{d}}}}E\tau (E)\big(-\frac{\partial f(E,\mu,T)}{\partial E}\big){(E-\mu )}^{n}\), f (E, μ, T) is the Fermi function, τ(E) is the energy-dependent transmission function, μ is the electrochemical potential, which we assume to be equal to the Fermi energy EF, and G0 = 2e2/h is the quantum of conductance. The low temperature limits for conductance and thermopower simplify to G = G0τ(EF) and \(S=-\frac{{\pi }^{2}{k}_{{{{\rm{B}}}}}^{2}T}{3e}\frac{{\tau }^{{\prime} }({E}_{{{{\rm{F}}}}})}{\tau ({E}_{{{{\rm{F}}}}})}\). The latter expressions provide an intuition, how G and S relate to the transmission τ(E) in Fig. 3a.

DFT calculations and further computational settings

We use TURBOMOLE 7.648 for all DFT calculations. We employ the def-SV(P) Gaussian basis set49 for all atoms, the PBE exchange-correlation functional50, converge energies to better than 10−7 Hartree (“scfconv 7”), and relax geometries until the gradient norm is below 10−3 a.u. (“gcart 3”). In the DFT+Σ correction, image charge planes in the molecular junctions are positioned 1.47 Å in front of fixed gold layers27,51. To obtain well converged results, we use 32 × 32 transverse k points for the construction of surface Green’s functions in quantum transport calculations.