Introduction

Traumatic brain injury (TBI) represents a critical global health challenge, emerging as one of the primary pathogenes to mortality and morbidity in modern society1. Intracranial pressure (ICP), which reflects the balance among brain tissue, cerebral blood volume, and cerebrospinal fluid within the skull, is one of the key diagnostic parameters for TBI management2. Anomaly-increased ICP is the most common cause of death in patients having severe TBI3 due to compromised cerebral blood flow, brain ischemia, inflammation, secondary neurovascular damage, and brain herniation4. This indeed necessitates swift intervention to mitigate risks such as brainstem compression and compromised brain circulation3. Consequently, precise and continuous monitoring of brain physiological parameters is imperative to prevent irreversible damage to TBI patients5.

Present ICP monitoring in clinics predominantly relies on the implanting of intraventricular catheters6. However, this approach is fraught with drawbacks, including restricted patient mobility due to wire connections (catheters) and heightened risks of complications like infection and hemorrhage, which may further worsen brain damage or result in new neurological disorders7. Although various non-invasive systems have been developed8,9,10 in the recent past, their effectiveness has been compromised by the ICP range, rendering them inadequate for use alone in patients with severe TBI11,12. Additionally, these methods are prone to artifacts from patient movement and rely heavily on the assistance of the equipment operator13. To make things worse, many state-of-the-art transducers for ICP monitoring suffer from constraints typified by low sensitivity and insufficient resolution14,15, failing to detect tiny ICP fluctuations. On the other hand, multimodal monitoring16 in addition to the information on ICP is also desired for clinical diagnostics, which, however, may unavoidably necessitate an extensive battery and therefore, exhibit low biocompatibility. Thus, multimodal monitoring poses additional challenges for the transducers to possess the ability of intrinsic information decoupling, high biocompatibility, and battery-free operation. Conventional capacitive pressure transducer (CPT) typically consists of two electrodes with a soft dielectric or air layer sandwiched between them. Despite its simple structure, CPT suffers from limited sensitivity, low-pressure resolution, and slow response speed17,18,19,20. To this end, recent advancements in ion-containing dielectric materials have made it possible to improve transducer performance. This iontronic capacitance transducer generates a dense concentration of electron-ion pairs at the interface between the dielectric layer and electrodes21,22, separated by mere nanometers23, thus significantly promoting the piezo-capacitive effect upon compressed and therefore exhibiting a more sensitive response24.

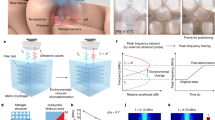
In addition to a high-performance transducer for ensuring the precise monitoring of ICP, wireless operation is also highly demanded to make the monitoring non-invasive, which has been typically realized by exploiting the inductor-capacitor (“LC”) oscillators (Fig. 1a). It is characterized by its simplicity and batteryless operation25,26, demonstrating significant potential in various biomedical sensing applications, including epidermal sensing for electrocardiogram (ECG) and plantar pressure measurement and the monitoring of intraocular27 and ICP28 in in-vivo scenarios. Nonetheless, despite the advantages of this conventional wireless passive sensing system, challenges still persist in terms of accuracy, resolution, robustness, stability, and interrogation distance29, which will be further exacerbated by tissue barriers such as the skull and dura mater in in-vivo scenarios. Recently, the concept of parity−time (PT) symmetry, which stems from quantum mechanics, has been extended to electronics, denoting that a non-Hermitian electronic system can still have purely real eigenspectra beyond a certain threshold, namely the exceptional point (EP)30. It has been reported that the eigenfrequencies of the system operating in the proximity of an EP may dramatically shift (Fig. 1b), greatly outperforming conventional “LC” wireless sensing (Fig. 1c)31. Such enhanced responsivity of EP-based devices has been successfully implemented in experiments32,33,34,35,36,37,38, showing great potential in biomedical sensing scenarios such as the monitoring of ICP.

Fig. 1: Non-Hermitian EP-based biotelemetric system.
figure 1

a Schematic of the EP-based biotelemetric system used for wireless ICP monitoring. b Circuit diagram of the PT-symmetric system in (i) and its spectral performance under different ICPs in (ii). c is similar to b but for the traditional “LC” wireless system.

Full size image

To this end, we propose an innovative biotelemetric ICP monitoring system (Fig. 1a), amalgamating a highly sensitive iontronic pressure transducer with the EP-based operation, whose circuit schematic is shown in Fig. 1b. In-vitro experiments demonstrate that the EP-based biotelemetric system has a sensitive response within the ICP range, and the maximum relative sensitivity in terms of frequency shift reaches 115.95 kHz/mmHg with a resolution of 0.003 mmHg, which significantly surpasses the current technologies by orders of magnitude. In-vivo experiments with a rabbit model demonstrate the EP-based biotelemetric system’s capability for multimodal detection regarding the ICP, heart rate, and respiratory rate. This multifunctionality could remarkably reduce the complexity of monitoring equipment and procedures. Our biotelemetric system operates effectively at detection distances unattainable by conventional “LC” wireless systems and demonstrates its superior performance exceeding three orders of magnitude over commercial instruments, revealing its great potential for medicine and clinical applications.

Results

EP-based ICP monitoring system

Figure 1a illustrates the diagram of the proposed EP-based biotelemetric system, which comprises an implantable sensor and an external reader for non-invasive (during the monitoring) physiological assessments. A standard second-order PT-symmetric circuit schematic is depicted in Fig. 1b(i). The external reader is an active oscillator (\(-{R}_{1}\), \({L}_{1}\), \({C}_{1}\)) while the passive oscillator (\({R}_{2}\), \({L}_{2}\), \({C}_{2}\)) forms the implantable sensor. It is attracting to compare it with the conventional “LC” wireless system [Fig. 1c(i)], which only retains a coil antenna (\({L}_{1}\)) in the reader to interrogate the same sensor. Without any perturbation (ignoring the transducer first in Fig. 2a) and applying Kirchhoff’s law to the resonating (oscillating as \({e}^{-i\omega t}\)) system, we can readily write the circuit dynamics [see details in Supplementary Material (SM) note 1], and the \(2\times 2\) non-Hermitian Hamiltonian reads

$${H}_{0}=\left(\begin{array}{cc}1-i\frac{1}{2{\gamma }_{1}} & -\frac{{\mu }_{12}}{2}\\ -\frac{{\mu }_{21}}{2} & 1+i\frac{1}{2{\gamma }_{2}}\end{array}\right),$$
(1)

where \({\gamma }_{1,2}={R}_{1,2}^{-1}\sqrt{{L}_{1,2}/{C}_{1,2}}\) is the non-Hermiticity of this non-Hermitian system, \({\mu }_{12,21}={M}_{12,21}/\sqrt{{L}_{1}{L}_{2}}\) denotes the inductive coupling strength and \({M}_{12,21}\) is the mutual inductance between the two coils. The PT symmetry condition requires that \([PT,{H}_{0}]\equiv PT{H}_{0}-{H}_{0}PT=0,\) leading to \({\gamma }_{1}={\gamma }_{2}=\gamma\) and \({\mu }_{12}={\mu }_{21}=\mu\); here, P denotes the parity operator associated with the first Pauli matrix and T is the time-reversal operator which takes the complex conjugation. Then, the eigenfrequencies in the unit of the resonance frequency (\({\omega }_{0}=1/\sqrt{LC}\)) yield

$${\omega }_{1,2}=1\pm \frac{1}{2\gamma }\sqrt{{\mu }^{2}{\gamma }^{2}-1}.$$
(2)
Fig. 2: Evolution of eigenfrequencies and reflection spectra as functions of asymmetrical perturbations.
figure 2

a Schematic of the equivalent circuit model for the EP-based biotelemetric system with an integrated ICP transducer. b The real part \({\mathrm{Re}}(\omega )\) (solid lines) and the imaginary part \({\mbox{Im}}(\omega )\)(dash lines) of the eigenvalues as functions of the normalized non-Hermiticity parameter \(\gamma /{\gamma }_{{{\rm{EP}}}}\). c Reflection spectra for the EP-based biotelemetric system with capacitive perturbations. Real eigenfrequency isosurface normalized by \({\omega }_{0}\) as a function of asymmetric capacitive perturbation \(\delta\) and dimensionless non-Hermiticity parameter \(\gamma\) (\(\mu=0.08\)) in (d), and coupling coefficient \(\mu\)(\(\gamma=23.32\)) in (e), respectively. Lines denote theoretical results while dots indicate experimental data.

Full size image

Invoking Eq. (2), one may quickly find that the eigenfrequencies may bifurcate and become purely real when \(\gamma > 1/\mu\) and become a complex conjugate pair when \(\gamma < 1/\mu .\) Indeed, this point is the EP dividing the system into the exact PT symmetry phase and the broken PT symmetry phase. This can also be observed in Fig. 2b, where \({\gamma }_{{{\rm{EP}}}}=1/\mu .\) Additionally, in the very vicinity of the EP, two eigenfrequencies may undergo a drastic shift with respect to the tiny variation of \(\gamma\), implying that such a characteristic may be implemented into the sensing scenarios. This indicates that such a circuit configuration may be highly sensitive to perturbations, which are induced by the ICP variation in this study, manifested by the significant frequency shift.

To this end, we next analyze the frequency response of the EP-based system when subject to asymmetric perturbations (i.e., the perturbation is introduced to the sensor end only). Here, we focus on the capacitive perturbations (\({C}_{2}^{\prime}=C+\Delta C\) and \(\delta=\Delta C/C < < 1\)) since later our transducer provides capacitive responses against pressure variations. Then, the perturbed Hamiltonian and the corresponding eigenfrequencies have the form of

$$H^{\prime}=\left(\begin{array}{cc}1-i\frac{1}{2\gamma } & -\frac{\mu }{2}\\ -\frac{\mu }{2} & 1-\frac{\delta }{2}+i\frac{1}{2\gamma }\end{array}\right),$$
(3)
$$\omega ^{{\prime} }_{1,2}=1-\frac{\delta }{4}\pm \frac{1}{4\gamma }\sqrt{({\delta }^{2}+4{\mu }^{2}){\gamma }^{2}-4i\delta \gamma -4}.$$
(4)

The analysis for the conventional “LC” system applies a similar approach, as detailed in SM note 2.

We notice here that in an electronic oscillator system, the resonance frequency (resonance dip in the reflection spectrum) probed by the port at the reader (Fig. 2a) is identical to the above eigenfrequencies only when the perturbation is small as the larger one will make the system not respect the PT symmetry anymore; here, it is worth noting that by connecting an isolated PT system into an input-output channel with the port impedance (\({Z}_{0}\)), \({R}_{2}={R}_{1}-{Z}_{0}\) should be ensured for the PT symmetry. We obtain the non-normalized frequencies (\({f}_{1,2}={\omega }_{0}\cdot \omega ^{{\prime} }_{1,2}/2\pi\)) from the reflectance spectrum as the monitoring targets for subsequent experiments. We can also see from Fig. 2c that when \(\Delta C\) is considerably large, the lineshape of the reflection coefficient probed by the reader will no longer exhibit the two sharp dips, indicating the breakdown of PT symmetry. Figure 2d, e are contour plots of two eigenfrequencies as functions of perturbations and system parameters (\(\gamma\) and \(\mu\)), which demonstrate a higher sensitivity when \(\gamma\) becomes smaller at the weak coupling regime. In addition, the two eigenfrequencies exhibit different responses to asymmetrical capacitive perturbations. \({\omega }_{1}\) shows a more pronounced frequency shift against the elevation of perturbation, while \({\omega }_{2}\) shifts gradually and diminishes as the strength of perturbation increases. On the contrary, when the perturbation is negatively added, \({\omega }_{2}\) displays a larger shift. The above analytical results demonstrate the efficacy of the EP-based system to detect the tiny capacitive perturbations by tracking the frequency shift, which will also be experimentally verified later.

High-Performance iontronic pressure transducer

Having introduced the theoretical framework of our ICP monitoring system, we now demonstrate the iontronic pressure transducers exploited in our work. One of the emerging methods to enhance the performance of pressure transducers is to utilize ionic materials as dielectrics, which can form an electric double layer (EDL) at the interface between the dielectric and electrode21,22. The EDL-based capacitive pressure transducer is distinguished by its broad detection range of pressure, high sensitivity, and excellent resolution. Consequently, they have been extensively explored for physiological pressure monitoring, wearable applications and robot operation, etc39,40,41,42,43.

To this end, we introduce the iontronic pressure transducer and conduct comprehensive characterization to ensure its efficacy for ICP monitoring. We show the preparation process of the ionic film in Fig. 3a, and the details are included in Methods. The iontronic pressure transducer features a sandwich-like structure, composing an ionic film [formulated from a mixture of Polyvinyl alcohol (PVA) and Phosphoric acid (H3PO4) as the intermediate dielectric layer] and two flexible electrodes (Fig. 3b), which can be equivalent to a shunt capacitor. The electrodes are made of a custom flexible printed circuit board (FPCB) with a 50 μm-thick polyimide film (PI) as the substrate, on which a 35 μm-thick copper (Cu) layer and a 25.4 nm-thick gold (Au) layer are deposited as the electrodes. This structure ensures not only biocompatibility and flexibility but also makes the device comply well with the skull’s curvature and the dura mater. As detailed in Fig. 3b, the ionic film contains a large number of low-molar positive and negative ion pairs. The electrons on the electrode and the counterions in the film come together in the contact area at a distance of nanometers to form EDL, establishing an interface capacitance or the so-called EDL capacitance44. The iontronic pressure transducer can achieve excellent capacitive response due to the ultra-high unit area capacitance (UAC), which varies with the actual contact area between the iontronic layer and the electrode21. When a tiny pressure is applied, the contact area increases drastically (characterized by \(\Delta A/{A}_{0}\)), directly leading to a significant alteration in corresponding capacitance; here  \(\Delta A\) is the change of contact area under external pressure and \({A}_{0}\) is the initial contact area.

Fig. 3: Design principle and characteristics of the iontronic pressure transducer.
figure 3

a Preparation process of the iontronic pressure transducer. b Schematic illustration of the iontronic pressure transducer and its equivalent circuit model. c Cross-sectional view and (d) top view of the ionic film obtained by scanning electron microscope (SEM). Similar result can be repeated for at least five times. e Simulated stress distribution visualizations for the ionic film with sandpaper-like architectures at varying applied pressures. f Dynamic capacitive response of the iontronic pressure transducer measured over time for pressures of 1,5, and 10 mmHg, respectively. g Capacitance-pressure responses under different temperatures. The sample size is \(n=3.\) Error bars representing the standard deviation of measurements. Data are presented as the mean values ± standard deviation. h Limit of detection (LOD) of the pressure transducer. i Response and recovery times of the transducer. j Long-term stability of the pressure transducer tested over 2000 cycles under a periodic pressure of 0 to 10 mmHg.

Full size image

To further augment the transducer’s sensitivity, we implement the sandpaper with 7000-mesh to produce a rough surface morphology on the ionic film. This process significantly improves the form factor (the ratio of the compressed area to the free expanded loadless surface area) and makes the EDL structure more deformable during compression. The microstructures created by the aforementioned process, as shown in Fig. 3c, d, have irregular shapes with approximately 5 μm width (see details in SM note 3). The intricate surface topology enlarges the effective contact area, boosting the capacitive response against the applied pressures. Consequently, this transducer can be versatile for various applications, including sophisticated human-machine interfaces and critical physiological information monitoring. According to the classical Persson theory in contact mechanics, the actual contact is manifested in the deformation of sharp structures on the surface when solid surfaces come into contact45. In our transducer, the synapse structure (the irregular microstructure) is crucial for improving its sensitivity and resolution. Finite element analysis (FEA) is conducted to elucidate deformations of microstructures under pressures using COMSOL Multiphysics software, and the results are shown in Fig. 3e. The film surface is simplified into irregular synapses-like posts for the simulation. These simulations illustrate the pressure-induced stress variations across the sandpaper-inspired topology under varying loading conditions. At a low initial pressure, only the tip of the synapses establish contact with the electrode. With increasing pressure, these synapses are compressed, allowing even the shorter ones to come into contact with the electrode and subsequently deform. When more pressure is applied, the film body is compressed. The contribution of the synapses-like microstructures to the transducer’s flexibility and compressibility is therefore evident.

The performance evaluation of our iontronic pressure transducer, at an operating frequency of 24 MHz, is meticulously conducted using a vector network analyzer (VNA) and a dynamometer, specifically focusing on the pressure fluctuation range relevant to ICP. Figure 3f illustrates a representative performance plot of the iontronic pressure transducer’s loading and unloading at pressures of 1, 5, and 10 mmHg. The transducer exhibits stable capacitive responses under these repeated loading and unloading cycles. The capacitance variation increases proportionally with the applied pressure and demonstrates identical responses to periodic pressure changes with rapid responses. Figure 3g illustrates the capacitance variation across a pressure range interested at different temperatures that are typical for normal and inflammatory intracranial environments46. The results indicate that temperature variations have a negligible impact on measurement results, affirming the transducer’s suitability for critical applications such as organ pressure and vital physiological sign monitoring. In addition, we also explore the limit of detection (LOD) of the pressure transducer (Fig. 3h) which is a critical variable for its application in scenarios where detecting minimal pressures is paramount. The transducer’s LOD is exemplified by its persistent signal above the noise floor, demonstrating an acute sensitivity to minimal pressure perturbations. Specifically, the transducer reliably responds to a minuscule periodic pressure change of 0.4 Pa ( ∼ 0.003 mmHg). The pressure variation is achieved by placing and removing a 1 mg weight on the 5 mm × 5 mm pressure transducer. From this, we can readily conclude that the transducer at least has a minimum pressure detection limitation of 0.4 Pa, significantly surpassing the current pressure transducer47,48,49. This is particularly important as an indication that our transducer has an extraordinary advantage in detecting tiny pressure signals and may be able to facilitate the monitoring of weak ICP fluctuations caused by respiration and heartbeats.

To determine the response time of the transducer, we construct a voltage divider circuit and utilize a high-speed oscilloscope for precise measurements (see details in SM note 4). The response time of the transducer depends on the speed at which the dynamometer applies pressure. To optimize this, we position the pressure bar of the machine as close as possible to the transducer and manipulate it at a maximum speed of 1000 mm/s to apply pressures and subsequently release the pressure from the transducer. Figure 3i illustrates the voltage responses in time domain, demonstrating the transducer’s rapid response (4.5 ms) and relaxation (8 ms) time. These results are significantly shorter than the typical fluctuations of ICP, and demonstrate not only the potential of the system for real-time monitoring applications with high resolution but also its capability to accurately track dynamic physiological changes, such as respiratory and heart rates—crucial for dynamic pressure sensing applications where temporal precision is paramount.

Furthermore, to assess the stability and repeatability of the transducer, we perform 2000 loading and unloading cycles under 10 mmHg pressure. The results, as presented in Fig. 3j, show that the transducer has a negligible capacitive response drift throughout these cycles, confirming its robustness and long-term reliability and stability. This endurance testing is crucial for ascertaining the transducer’s operational lifespan and reliability. Notably, even after extensive use, the iontronic pressure transducer still exhibits a consistent response, demonstrating its excellent mechanical stability and its suitability for continuous physiological monitoring over prolonged periods, which can be better understood from the zoomed-in illustration in Fig. 3j.

In-vitro validation of the EP-based biotelemetric system

Combining our analytical results of EP operation and the sensitive pressure transducer, we have practically developed the EP-based biotelemetric system using the FPCB. As depicted in Fig. 4a, the sensor end consists of a planar coil, an iontronic transducer, and a capacitor (\({C}_{2}\)), wherein the capacitor is connected in parallel with the iontronic transducer to eliminate its resistive parasitic effect (see details in SM note 5). The loss contribution of the sensor (\({R}_{2}\)) is the internal resistance of the “LC” oscillator. By mounting the iontronic pressure transducer at the sensor end on the dynamometer and connecting the flexible coil via enameled wires, we can easily apply the pressures at will. Through meticulous adjustment of the resistance and capacitance at the reader end, the system operates adjacent to the EP and monitors the correlation between frequency shifts and pressure changes via the reflection spectra using the VNA. By doing so, we first measure the eigenfrequencies under different \(\mu\) and \(\gamma\), which are included in Fig. 2d, e with the blue dots, showing great agreement with the theoretical predictions.

Fig. 4: Sensitive response of the EP-based biotelemetric system.
figure 4

a Schematic illustration of the EP-based biotelemetric system. b Evolution of reflection spectra for the EP-based biotelemetric system at pressures of 0, 0.2, 1.0, 6.0, and 9.5 mmHg. c Frequency shift of the EP-based biotelemetric system as a function of applied pressure. The dashed lines denote simulation results. d Quality factor of eigenfrequencies as a function of applied pressure. e Reflection spectrum and f detailed change in eigenfrequency at the minimum pressure. g Reflection spectra when applied with (solid) and without (dashed) an acrylic plate mimicking the skull placed in-between the two coils. h Frequency shift versus pressure differential centered around a baseline pressure of 5 mmHg. The dashed lines denote simulation results. Reflection spectra for the EP-based biotelemetry system (i) and the conventional “LC” system (j) under different applied pressures.

Full size image

The physiological range of ICP for a healthy adult is 7−15 mmHg at rest50, with levels above 20 mmHg considered pathologically significant and above 40 mmHg extremely dangerous51. Raised ICP is also known as intracranial hypertension and is defined as a sustained ICP of greater than 20 mmHg52. Therefore, our EP-based biotelemetric system primarily focuses on responses within this critical ICP fluctuation range (ΔP < 10 mmHg), beyond which medical intervention is considered to be necessary. Figure 4b displays representative reflection spectra (from 21.5 MHz to 25 MHz) of the EP-based biotelemetric system measured under different pressures (0, 0.2, 1.0, 6.0, and 9.5 mmHg), noting that the system maintains PT symmetry and operates close to the EP in the absence of pressure. The system works under weak coupling (\(\mu=0.08\)) to ensure the implementation of in-vivo experiments (see details in SM Fig. S2). The eigenfrequencies bifurcation effect and two distinct eigenmodes rendered by two steep reflection dips can be observed. However, the capacitance of the iontronic transducer increases as pressure is applied, driving the system to operate a bit away from the EP, resulting in a drastic frequency shift.

We determine the eigenfrequencies from the reflection spectra, as depicted in Fig. 4c, which demonstrates an excellent response to pressure variation within the ICP fluctuation range. The experimental results exhibit excellent agreement with the simulations. Initially, the system operates in the vicinity of EP with no pressure applied. Subsequent pressure application drives the system operating away from the EP and induces a frequency shift. The larger eigenfrequency (\({\omega }_{2}\)) displays a more extensive pressure detection range, although its frequency variation is slightly less pronounced than that of the lower eigenfrequency (\({\omega }_{1}\)). The inset of Fig. 4c further illustrates the response of the EP-based biotelemetric system under extremely low pressure, showing similar responses between the two eigenfrequencies to pressure changes. We define the sensitivity of the EP-based biotelemetric system as \(S=\Delta f/\Delta P\), which is represented by the change in resonance frequency per unit pressure, where \(\Delta f\) and \(\Delta P\) denote the eigenfrequency changes and applied pressure, respectively. Remarkably, our system exhibits a high sensitivity of 115.95 kHz/mmHg for low pressure ( < 2 mmHg). This extraordinary sensitivity is attributed to the synergetic effects of the high performance of EDL-based iontronic transducer and the sensitivity enhancement of EP. We include a comparison among the current state-of-the-art designs of the pressure monitoring systems in SM note 6. These demonstrate potential for application in which ICP fluctuation must be monitored with high fidelity. Figure 4c additionally shows a limited pressure detection range up to 5 mmHg for \({\omega }_{1}\). Moreover, the quality factor (defined by \(Q={f}_{0}/BW\), where BW is the 3 dB bandwidth) becomes the largest when closing the EP, i.e., the optimal resolution as seen in Fig. 4d. However, as the pressure increases (and consequently capacitance increases), the quality factor degrades for both eigenfrequencies and the \({\omega }_{1}\) becomes increasingly difficult to distinguish, particularly when the pressure exceeds 5 mmHg. The \({\omega }_{2}\) is extremely sensitive (115.95 kHz/mmHg) in small pressure ranges (0−2 mmHg) and still has a recognizable resolution in large pressure ranges (2 − 10 mmHg), making it more suitable as the observation target for ICP monitoring.

In addition, we investigate the system’s capability to detect extremely low pressure. The strong response of the EP-based biotelemetric system to weak perturbations raises potential concerns about the noise impact on the performance53. While the system exhibits enhanced sensitivity to the target perturbations around EP, any unwanted noise existing in the system will also be amplified in the same magnitude. However, this noise-introduced frequency fluctuation is indeed ignorable compared to the frequency shift caused by the actual pressure variations (see details in SM note 7). Furthermore, Fig. 4e presents the reflection spectra of the EP-based biotelemetric system before and after applying a pressure of 0.4 Pa ( ∼ 0.003 mmHg), as well as Fig. 4f displays the corresponding waveforms for the two eigenfrequencies. This demonstrates frequency differentiation under extremely weak pressure perturbations. These results illustrate that our system can even discern pressure changes at the level of 10−3 mmHg, significantly surpassing the performance of currently available ICP monitoring systems28,51,54,55,56, and therefore, suggesting the sensor’s potential in scenarios where detecting subtle pressure variations is critical, even the most negligible pressure differences are of significant consequence. Furthermore, we use an acrylic plate to investigate the impact of the skull on the system. Figure 4g compares the measurements conducted with and without acrylic plate between the coils under the same conditions, revealing minimum influences on the reflectance spectra. This underscores the reliability of our EP-based biotelemetric system in realistic physiological conditions. Figure 4h explores the differential pressure response of our system by examining frequency shifts relative to a pressure differential from a baseline of 5 mmHg, providing insights into the system’s precision across a dynamic range. By setting a base pressure of 5 mmHg and conducting the EP operation, the system’s response to both increase and decrease in pressure is recorded. The results highlight the system’s heightened sensitivity to both increasing ordecreasing applied pressures. This particularly demonstrates the system’s utility in environments where monitoring pressure drop is vital.

A comparative analysis with a conventional “LC” wireless sensing system further emphasizes the advantages of our system. Figure 4i, j display the reflection spectra of our EP system and the conventional “LC” wireless sensing system. The EP-based biotelemetric system exhibits higher resolution with higher Q-factors and sensitive frequency responses to various pressures at distances that traditional “LC” sensing systems cannot respond to (see details in SM note 8). These observations suggest that the EP-based biotelemetric system could provide enhanced performance for diagnostic and monitoring applications, offering significant improvements over traditional methods.

In-vivo ICP monitoring by EP-based biotelemetric system

For the in-vivo validations, we encapsulate the flexible pressure sensor with a 20 μm polydimethylsiloxane (PDMS) film (1 cm × 1 cm dimension as detailed in SM note 9) to prevent water loss of the ionic film and moisture ingress from the environment. We implant the EP-based biotelemetric sensing module into the brains of rabbits (Fig. 5a) to measure the dynamic fluctuations of ICP.

Fig. 5: Multimodal detection of EP-based biotelemetric systems.
figure 5

a Schematic illustration of the EP-based biotelemetric system implanted in an animal model. b Schematic illustration of the EP biotelemetry sensing principle for the ICP monitoring. c A sequential depiction of the implantation procedure, demonstrating the steps taken to insert the sensing module into the animal. d Comparative frequency signals captured by the EP-based biotelemetric system and a conventional commercial intracranial pressure instrument before and after epinephrine injection. e Respiratory rate changes induced by pharmacologic interventions. f A representation of continuous ICP signal monitoring. g Extracted heart rate signal, corroborated against a standard ECG reading.

Full size image

Our ICP monitoring setup, illustrated in Fig. 5b, c, requires placing the sensor within the gap between the skull and dura to facilitate ICP sensing and wireless transmission. The external reader is delicately positioned above the implanted device to make the system operate around the EP and wirelessly acquire the data. According to the above analytical results, we exploit \({\omega }_{2}\) to monitor the fluctuation of ICP, and \({\omega }_{0}=2\pi {f}_{0}\) with \({f}_{0}\approx 24.1\) MHz. The calibration between the frequency shift and the ICP variation is then conducted. In addition, we implement a commercial probe into the brain to serve as a comparative reference. We use the AD8232 sensor and Arduino setup for additional monitoring of the cardiac and respiratory functions of the rabbit. The implantation procedure includes craniotomy, device implantation, and skull reduction, which are described in detail in the Methods.

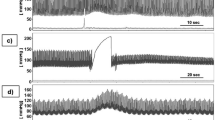
The sensor translates the ICP fluctuations of the rabbit into frequency signals, which will be interrogated by the reader outside the skull and displayed by the VNA and laptop. In the demonstration of ICP monitoring, we conduct continuous ICP monitoring for up to 800 s and induce a drastic change in ICP by injecting 0.1 mL epinephrine (1 mg/mL) into the rabbit’s vein at 90 s. Figure 5d illustrates the time-dependent frequency response, capturing the acute pressure response to the injection of epinephrine. The eigenfrequency shows a sharp variation corresponding to the rapid ICP rise, gradually recovering to the baseline as the drug’s effect fades away. Compared with data from the commercial ICP probe (yellow line) which exhibits stepwise changes and low temporal resolution due to its 1 mmHg measurement precision, our system displays superior precision and resolution, effectively capturing subtle physiological changes. Meanwhile, the trend of frequency change obtained by our device is briefly consistent with that recorded simultaneously by the commercial ICP sensor.

Further evaluation of the extraordinary sensitivity of the EP-based biotelemetric system is provided by an enlarged view of the frequency fluctuations before and after the epinephrine injection, with Fig. 5e highlighting the respiratory rate variation. The extracted signal shows that our system detects an increase in breathing rate after (stage II in Fig. 5d, ~21 times per minute) epinephrine injection compared to that before injection (stage I in Fig. 5d, ~15 times per minute), while the commercial ICP sensor could only measure large pressure changes. The system’s high-resolution capabilities are evident, detecting even subtle ICP changes caused by breathing, which conventional ICP sensors are unable to do. The capability to capture these changes with high resolution is not only indicative of its superb sensitivity but also of its potential to supersede traditional monitoring systems in capturing rapid physiological fluctuations in a clinical setting. The amplified and filtered frequency signals in Fig. 5f further corroborate the system’s ability through continuous monitoring of physiological signals. The signal envelope exhibits distinct spikes corresponding to the rabbit’s breathing. The eigenfrequency produces a spike signal as the rabbit breathes. By tracking the frequency of this signal, we can accurately measure the breathing rate of the rabbit ( ~ 21 breaths per minute, indicating proper maintenance of anesthesia). In addition, the frequency signal fluctuates periodically with a smaller amplitude, and details can be captured after amplifying the signal. The enlarged Fig. 5g (zoom-in window of Fig. 5f) distinctly contrasts the heart rate signals extracted from the system with a conventional ECG, it is found that the similarity between the extracted heart rate signal and the ECG readings is striking ( ~ 220 beats per minute). This observation can also be validated by the fast Fourier transformation (FFT) analysis of ICP signals, as detailed in SM note 10, underscoring the system’s powerful ability to provide real-time, accurate physiological monitoring.

This in-vivo ICP monitoring indeed highlights our EP-based biotelemetric system’s profound sensitivity and specificity in detecting and monitoring physiological signals. It exhibits remarkable performance, demonstrating not only the capability to monitor pressure changes with exceptional precision but also the ability to extract minor ICP fluctuations induced by respiration and cardiac dynamics. Such multimodal detection capability is particularly relevant and important in clinical settings, enabling the detection of respiratory changes and arrhythmias associated with increased ICP, thus informing the timely adjustment of medication.

Discussion

In this work, we have proposed an EP-based biotelemetric system for continuous and real-time wireless ICP monitoring facilitated by an iontronic capacitive pressure transducer. The utilization of the EP degeneracy integrated with the iontronic transducer having high sensitivity significantly enhances the reliability, resolution, and sensitivity of the ICP monitoring process. Remarkably, the EP-based biotelemetric system can achieve a highly sensitive response with a maximum relative sensitivity of 115.95 kHz/mmHg within the ICP fluctuation range, which is nearly an order of magnitude higher than those by current sensing systems. Moreover, the system’s capabilities extend to detecting pressure variations as subtle as one-thousandth of a millimeter of mercury, which far exceeds the accuracy of commercial ICP sensors. The practical efficacy of the biotelemetric system has been validated through in-vivo experiments conducted on a rabbit model. Our results demonstrate the system’s unparalleled sensitive response compared to commercial ICP probes. We have further shown the system’s ability to accurately identify various degrees of pressure signals and perform multimodal detection. The superior sensitivity and resolution enable the system to detect minute ICP fluctuations caused by physiological processes such as respiration and cardiac activity. In a word, the system not only monitors ICP but also concurrently tracks respiratory and heart rates, simplifying clinical procedures and enhancing clinical utility by providing a comprehensive monitoring solution in a single device. The integration of such a biotelemetric system into bio-implantation practices holds significant promise for healthcare applications, particularly in the continuous monitoring of vital signs.

Methods

Preparation of ionic films

First, 2 g polyvinyl alcohol (PVA, MW ≈ 145000, Aladdin Industrial Corporation) is dissolved into 18 g deionized (DI) water by magnetic stirring at 90 °C for 2 hours. After cooling the solution to room temperature, 1.65 mL phosphoric acid (H3PO4, GR, ≥ 85% in H2O, Shanghai Macklin Biochemical Co., Ltd.) is added and stirred at room temperature (22 °C) for another 2 hours. Next, the PVA/H3PO4 mixture is poured onto the 7,000-mesh sandpaper and spin-coat for 30 s at a speed of 100 rads/min using a spin coater (EZ6, Schwan Technology Co., Ltd.). Then, the mixture is dried at room temperature for about 12 hours until the water evaporates and forms an ionic film on the sandpaper.

Characterization of iontronic transducer and biotelemetry system

The microstructure of PVA/H3PO4 films is characterized by a field-emission scanning electron microscope (FESEM, Model SU5000, Hitachi, Ltd.). An electrochemical workstation (CHI 660E, CH Instruments, USA) is used for electrochemical characterization. External pressure is precisely applied and measured using a computer-controlled dynamometer (F105, MARK-10, ltd.). The response time of the transducer is tested using an oscilloscope (Model EXR104A, KEYSIGHT). Frequency signals are acquired using the vector network analyzer (Rohde & Schwarz ZNLE3).

Animal experiment

Three male New Zealand white rabbits (2.5–3 kg, 14–16 weeks, specific pathogen-free grade) serve as the subjects in our in-vivo experiments to demonstrate systems’ performance. All surgical and experimental procedures involving live animals conform to the Guide for the Care and Use of Laboratory Animals and the compulsory laboratory animal facility standard of China, and are approved by the Institutional Animal Care and Use Committee of Zhejiang University, China (No. ZJU20230269). Animals are fully acclimatized to the environment for seven days before any experimental procedure and are given standard chow and water. The following procedures is performed on rabbits to measure their ICP using our sensor and a commercial ICP probe (Codman microsensor 826631, Integra LifeSciences Production Corporation). First, atropine (0.08 mg/kg) is administered via subcutaneous injection to prevent bradycardia or decrease secretions. Then, ketamine (20 mg/kg I.M.) is used as an anesthetic agent. Next, the head and ears of the rabbits are shaved and fixed in a stereotaxic head frame. After applying lidocaine to the rabbit scalp for local analgesia, the head is disinfected, make an incision on the scalp, and hydrogen peroxide (H2O2) is applied to expose a dry and clean skull. 20 mL of 20% mannitol is injected intravenously to reduce ICP and prevent cerebral edema after craniotomy. A cranial window about 5 mm × 10 mm in size is drilled. The dura mater is separated from the skull around the cranial window by blunt dissection and the sensor and the commercial ICP probe are inserted under the adjacent skull. Then the skull is closed by placing back the removed skull piece. The system parameters are adjusted to the EP operation and record the frequency signal using a VNA. Then, 0.1 mL of epinephrine (1 mg/mL) is injected intravenously to increase ICP. After 120 seconds, the effect of epinephrine wears off and the ICP gradually decreases. The data from the commercial ICP probe is displayed and recorded by the ICP monitor (Codman ICP Express Monitor 82-6635, Integra LifeSciences Production Corporation) and a patient monitor (BeneView T5, Mindray Bio-Medical Electronics Co., Ltd).

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.