Isolating Cu-Zn active-sites in Ordered Intermetallics to Enhance Nitrite-to-Ammonia Electroreduction

Abstract

Electrocatalytic nitrite reduction to the valuable ammonia is a green and sustainable alternative to the conventional Haber-Bosch method for ammonia synthesis, while the activity and selectivity for ammonia production remains poor at low nitrite concentrations. Herein, we report a nanoporous intermetallic single-atom alloy CuZn (np/ISAA-CuZn) catalyst with completely isolated Cu-Zn active-sites, which achieves neutral nitrite reduction reaction with a remarkable NH₃ Faradaic efficiency over 95% and the highest energy efficiency of ≈ 59.1% in wide potential range from −0.2 to −0.8 V vs. RHE. The np/ISAA-CuZn electrocatalyst was able to operate stably at 500 mA cm⁻² for 220 h under membrane electrode assembly conditions with a stabilized NH₃ Faraday efficiency of ~80% and high NO₂^‒ removal rate of ~100%. A series of in situ experimental studies combined with density functional theory calculations reveal that strong electronic interactions of isolated Cu-Zn active-sites altered the protonation adsorption species, effectively alleviating the protonation barrier of *NO₂ and thus greatly facilitating the selective reduction of NO₂⁻ into NH₃.

Introduction

Ammonia (NH₃), as one of the most globally important chemicals, is mainly produced through Haber-Bosch process, which inevitably results in 1–2% of global energy consumption and 1–2% of global CO₂ emissions^1,2,3,4,5. As an alternative route, utilizing hydrogen from water to electrochemically reduce nitrite (NO₂^‒) as the nitrogen source is attracting more attention^6,7,8. The nitrite species are a widespread pollutant in industrial wastewater, liquid nuclear waste, livestock excrement, and chemical fertilizers, thereby threatening human health^9,10,11,12. Therefore, the direct electrochemical NO₂^‒ reduction reaction (NO₂RR) under ambient conditions using renewable electricity is an attractive strategy to convert toxic NO₂^‒ into valuable product NH₃, which could result in the production of a clean hydrogen carrier while simultaneously treating pollution sources^6,7,8,13,14. Despite significant advances in the development of electrocatalysts in recent years, the direct electrosynthesis of ammonia with high selectivity remains a great scientific challenge. This obstacle is largely due to the complicated reaction pathway with sluggish kinetics and side reactions such as hydrogen evolution reaction (HER), electroreduction to nitrogen (ERN₂), and electroreduction to nitric oxide (ERNO) affect multiple elementary steps simultaneously, especially in the low concentration of actual nitrite resources^4,15,16. Therefore, the rational design of advanced electrocatalysts that can selectively electroreduction NO₂⁻ to NH₃ with high-density active-sites and suitable rate-determining step (RDS) energy barriers is highly desirable.

Copper (Cu)-based nanostructures have recently emerged as promising electrocatalysts for converting NO_x species to NH₃ under ambient conditions^{16,17,18,19,20}. However, conventional copper catalysts usually have a high protonation barrier, which promotes competing HER reactions and side reactions (ERN₂, ERNO, etc.), thereby leading to selectivity for the desired NH₃ product^19,20. In this regard, anchoring metal single atoms on ideal substrates have been emerged as an efficient strategy to tuning the electronic structure of single atom catalysts (SACs) through low surface densities^21,22,23. Through this strategy, the catalytic reaction pathway may be altered and the adsorption/desorption properties of the relevant reaction intermediates can be optimized to achieve the ideal catalytic performance^23,24. But in light of actual conditions, the supported single-atom catalysts cannot offer the ability to create each well-defined metal atom with uniform activity and a stable local coordination environment, which are obstacles for revealing the roles of geometric and electronic structure on the catalytic properties. In contrast, ordered intermetallic single-atom alloys (ISAAs) are recently deemed to represent a structural motif, where might be isolated to single atom on intermetallic structures orderly with the insertion of a relatively inert metal (IM) to form the highest density isolated IM-M active-sites^17,24,25,26. Besides, the isolated IM-M active-sites in ISAAs lead to the moderate the adsorption/desorption ability of reaction/intermediates species and optimize the reaction pathways, leaving possibility of catalyzing the reaction in the desired direction^27,28. Moreover, the catalyst with nanoporous structure can effectively extend the residence time of the low-concentration reactants, which substantially increased the accessibility of the reactants thereby further boosting the selectivity to ammonia^29,30,31,32. Nevertheless, producing controlled compositions of ISAAs that contain elements with large differences in reduction potential remains challenging, particularly for alloys consisting of transition metals, which makes it difficult to simultaneously control the phase and morphology of the nanostructured ISAAs by conventional solution/high temperature-phase synthetic methods.

In this work, we report an intermetallic single-atom alloy Cu-Zn with bicontinuous nanoporous structure, which offers consistent highest density isolated Cu-Zn active-sites throughout the catalyst to promote neutral NO₂RR for selective NH₃ electrosynthesis. As a result, our np/ISAA-CuZn enables high selectivity NO₂^‒-to-NH₃ performance, with excellent NH₃ Faradaic efficiency over 95% and high energy efficiency in a wide potential range from −0.2 to −0.8 V vs. reversible hydrogen electrode (RHE). Using membrane electrode assembly (MEA) electrolyzer, the np/ISAA-CuZn electrocatalyst exhibits excellent stability of 220 h of continuous NO₂RR at 500 mA cm⁻² with a near-constant FE of ~80% and the NO₂^‒ removal rate of ~100%, which is sufficient to meet the drinking water standard. More importantly, this high nitrite reduction catalytic activity enables the selective conversion of 1 mM nitrite to ammonia with Faradaic efficiency of over 90.9% at −0.5 V vs. RHE. In situ X-ray absorption spectroscopy (XAS) and in situ attenuated total reflectance surface-enhanced infrared absorption spectroscopy (ATR-SEIRAS) coupled with density functional theory (DFT) calculations reveal that the high activity of the np/ISAA-CuZn catalyst can be attributed to the strong electronic interaction between the complete isolated Cu-Zn active-sites, which modulates the protonation adsorption species and effectively reduces the *NO₂ protonation energy barriers, thus enhancing the NO₂RR activity.

Results

Materials synthesis and characterization

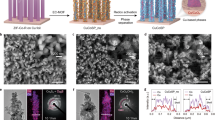
The precise synthesis of nanoporous ordered intermetallic Cu-Zn was carried out using an electrochemically selective phase dissolution and transformation method at room temperature, as illustrated schematically in Fig. 1a. Firstly, the Cu_xZn_1–x (at%, x = 6, 15) precursor alloy with two phases of the hexagonal close-packed metallic Zn and the hexagonal close-packed intermetallic CuZn₅ were fabricated by an arc-melted method (Supplementary Fig. 1). Then the intermetallic CnZn₅ could be created through selectively etching the active Zn phase by electrochemical selective phase dissolution approach in 1 M KOH solution (Supplementary Figs. 2–4). Subsequently, a series of intermetallic compounds (IMCs) of nanoporous CuZn₄ (denoted as np/CuZn₄), nanoporous Cu₅Zn₈ (denoted as np/Cu₅Zn₈), nanoporous intermetallic single-atom alloy CuZn (denoted as np/ISAA-CuZn) with a uniform nanoporous structure were synthesized from the conversion of np-CnZn₅ through an electrochemically induced phase transformation under different operated potentials (Supplementary Figs. 2 and 3), which allows Zn atoms to be instantaneously dissolved from the lattice during the electrochemical corrosion process, initiating the interdiffusion of atoms and the rearrangement of the crystal to an intermetallic phase (Fig. 1b and Supplementary Figs. 5–9)^32,33,34. Scanning transmission electron microscopy (STEM) image of np/ISAA-CuZn exhibits a uniform nanoporous architecture composed of interconnective ligaments (Fig. 1c), which has an ultrafine pore size of ~2.9 nm and a higher specific surface area of ~22.14 m² g⁻¹ (Supplementary Fig. 10). The ordered atomic structure of np/ISAA-CuZn is further identified by aberration-corrected high-angle annular dark-field STEM (HAADF-STEM) (Fig. 1d, e), which displays the surface atomic arrangement of body-centered cubic (bcc) CuZn IMC along the [$\bar{1}11$] and $[001]$ zone axes, respectively. The labeled d-spacing of 0.21 nm and 0.15 nm could match well with the (110) and ($200$) planes of bcc CuZn structure, respectively, in agreement with the atomic arrangement of the Pm3̅m CuZn crystal structure model projected along the [$\bar{1}10$] direction (Fig. 1f). It is noteworthy that a high density of atomic steps is presented on the np/ISAA-CuZn ($200$) surface (along the axis of [$001$] zone), indicating abundant atomic defects and unsaturated coordination atoms at the edge of np/ISAA-CuZn ligaments (Fig. 1e). In addition, elemental mapping of energy dispersive X-ray (EDX) spectra and high-resolution EDS line scans of the np/ISAA-CuZn surface show homogeneous and well-mixed distribution of Cu and Zn elements (Fig. 1g and Supplementary Fig. 11), indicating that no segregation occurred, which is confirmed by inductively coupled plasma optical emission spectrometer (ICP-OES) results (Supplementary Table 1).

Fig. 1: Fabrication and structural characterization of nanoporous Cu-Zn IMCs.

a Schematic illustration of preparation processes for np/CuZn₄, np/Cu₅Zn₈, np/ISAA-CuZn, and np/Cu. b XRD spectra of np/CuZn₄, np/Cu₅Zn₈, and np/ISAA-CuZn. c HAADF-STEM image of np/ISAA-CuZn, d, e Enlarged high-resolution HAADF-STEM images. f Crystal structure of np/ISAA-CuZn with ordered, bcc structure and its projection in the [$1\bar{1}0$] direction. g Elemental mapping of np/ISAA-CuZn, Scale bars: c 5 nm, d, e 1 nm, g 20 nm.

XAS was utilized to explore the electronic interactions and coordination environment of Cu and Zn sites over the nanoporous Cu-Zn IMCs at the atomic scale. The Cu K-edge X-ray absorption near edge structure (XANES) spectra of the nanoporous Cu-Zn IMCs are similar to that of the Cu foil (Fig. 2a), while the spectra for the nanoporous Cu-Zn IMCs shift to lower energy absorption edge compared to the Cu foil, suggesting the electron transfer from Zn to Cu^35,36,37. Figure 2b shows the normalized Zn K-edge XANES spectra of the nanoporous Cu-Zn IMCs and the references of Zn foil and ZnO powders. Specifically, the higher absorption edge of the nanoporous Cu-Zn IMCs approaching those of Zn foil imply a higher valence state of Zn in nanoporous Cu-Zn IMCs than that in Zn foil. Interestingly, as the Cu/Zn ratio in nanoporous Cu-Zn IMCs increases, the valence state of Cu decreases and the corresponding valence state of Zn increases (Supplementary Fig. 12). This indicates that the electronic interactions between Cu and Zn atoms gradually increase with the increase of the Cu/Zn ratio, leading to more electrons are transferred from Zn to Cu in np/ISAA-CuZn^37,38. The presence of CuO or ZnO can be ruled out as the Cu/Zn-O bond is not observed in the R-space data of the Fourier transform extended X-ray absorption fine structures (FT-EXAFS) plot (Fig. 2c, d). Moreover, the dominant peaks of Cu K-edge FT-EXAFS spectra of CuZn₄, Cu₅Zn₈, and CuZn IMCs show a slight shift relative to that of the Cu foil (Fig. 2c). The similar tendency is also observed on the Zn K-edge FT-EXAFS spectra (Fig. 2d). These results indicate the change of atomic distances in nanoporous Cu-Zn IMCs^17,20. This is further strengthed by the wavelet transformed EXAFS (WT-EXAFS) contour plots in Fig. 2e and Supplementary Fig. 13. Notably, the radial distance positions of both Cu and Zn k-edge EXAFS shift toward lower values as the Cu/Zn ratio increased, which is caused by the change of Cu and Zn coordination environments in different nanoporous Cu-Zn IMCs^38,39,40. The EXAFS fittings were further performed to obtain the quantitative structural configuration of Cu and Zn in the nanoporous Cu-Zn IMCs (Supplementary Table 2). The Cu and Zn K-edge EXAFS fitting results of np/ISAA-CuZn show that the coordination numbers (CN) of Cu and Zn are 4.5 and 3.2, respectively, which are lower than the theoretical coordination number (8), confirming the low coordinate environment of Cu and Zn atoms in np/ISAA-CuZn. Significantly, the coordination numbers of the first nearest Cu-Cu/Zn-Zn bond decrease to zero for the np/ISAA-CuZn, indicating the absence of the Cu-Cu/Zn-Zn bond. Therefore, the Cu and Zn atoms are completely segregated to form isolated Cu-Zn active sites, which are in good agreement with the CuZn crystal structure in an ordered intermetallic bcc phase.

Fig. 2: X-ray absorption spectroscopy analysis.

a Normalized Cu K-edge XANES spectra of np/CuZn₄, np/Cu₅Zn₈, np/ISAA-CuZn, Cu foil and CuO. b Normalized Zn K-edge XANES spectra of np/CuZn₄, np/Cu₅Zn₈, np/ISAA-CuZn, Zn foil and ZnO. c The corresponding Cu K-edge FT-EXAFS spectra. d The corresponding Zn K-edge FT-EXAFS spectra. e The corresponding Cu K-edge WT-EXAFS spectra.

Electrocatalytic Performance of NO₂RR

The electrochemical NO₂RR performance of the catalysts were investigated under ambient temperature and pressure in a standard three-electrode H-type cell. Nanoporous Cu (np/Cu) was also prepared using a similar method as comparasion (Supplementary Figs. 14 and 15). As shown in Supplementary Fig. 16, the linear sweep voltammetry (LSV) curves recorded by np/ISAA-CuZn in 0.2 M KHCO₃ solution with 10 mM KNO₂ show a larger increase in current density than that without NO₂^‒, indicating that a rapid NO₂^‒ reduction occurred^41,42. Figure 3a shows the LSV curves of np/CuZn₄, np/Cu₅Zn₈, np/ISAA-CuZn, and np/Cu in the electrolyte containing KNO₂ (10 mM) and KHCO₃ (0.2 M). The np/ISAA-CuZn exhibits a much more positive onset potential than that of np/CuZn₄, np/Cu₅Zn₈, and np/Cu, indicating that NO₂^‒ efficient protonation on the np/ISAA-CuZn³⁷. Indophenol blue spectrophotometry was used to quantify the NH₃ produced by the catalysts and thus reveal the selectivity of the catalyst in converting NO₂^‒ to NH₃ (Supplementary Fig. 17)⁴³_. The NH₃ FE and yield rate of the electrocatalysts are shown in Fig. 3b, c. The results showed that NH₃ was the only liquid product derived from the np/ISAA-CuZn catalyst, together with a small amount of N₂ and H₂ (Supplementary Fig. 18). The np/ISAA-CuZn exhibits over 95% NH₃ FE in a wide potential range from −0.2 to −0.8 V vs. RHE, and an exceedingly high yield rate of 11.8 mg h^‒1 mg^‒1 at −1.0 V vs. RHE (Supplementary Fig. 19a), outperforming most of the reported catalysts^13,41,44,45. However, a significant decrease in NH₃ FE occurred at high potentials (Supplementary Fig. 19b), which is mainly attributed to the lack of reactant supply due to the drastic decrease in local NO₂^‒ concentration at high potentials, resulting in the enhancement of the competitive reaction HER³. Partial current densities of NH₃ normalized according to electrochemically active surface area (ECSA) confirm that np/ISAA-CuZn possessed the highest intrinsic activity compared to the other catalysts (Supplementary Fig. 20). Furthermore, the energy efficiency (EE) of the np/ISAA-CuZn is further evaluated, which shows a high EE over 40% in a wide potential range (−0.2 to −0.8 V vs. RHE), and an exceedingly high EE of 59.1 ± 1.5% at −0.2 V vs. RHE (Fig. 3d).

Fig. 3: Electrocatalytic performance for the NO₂RR.

a LSV of np/CuZn₄, np/Cu₅Zn₈, np/ISAA-CuZn and np/Cu in 0.2 M KHCO₃ + 10 mM KNO₂. b-d The corresponding NH₃ FE (b), NH₃ yield rate (c), and EE (d) of np/CuZn₄, np/Cu₅Zn₈, np/ISAA-CuZn and np/Cu at different applied potentials in 0.2 M KHCO₃ + 10 mM KNO₂. e Quantification of NH₃ via Indophenol and IC measurements at −0.5 V vs RHE. f ¹H NMR measurements of produced ammonia using ¹⁴NO₂^‒ and ¹⁵NO₂^‒ as feeding N sources of np/ISAA-CuZn. g NH₃ FE and yield rate for np/ISAA-CuZn at a series of potentials in 0.2 M KHCO₃ + 1 mM KNO₂. h Long-term electrocatalytic stability of the NO₂RR (0.2 M KHCO₃ + 10 mM KNO₂) over np/ISAA-CuZn at 500 mA cm⁻² using the MEA electrolyzer. Blue arrows indicate the renewal of fresh electrolytes. The error bands represent the standard deviation of the data obtained from more than three repetitions.

To further verify the experimental results, NH₄⁺ concentrations in the solution before and after the reaction were examined using ion chromatography (IC) (Fig. 3e). Notably, the calculated values of NH₃ yield rate and the FE match well with the indophenol blue tests. Furthermore, we found that all ammonia produced by the reaction were generated from nitrite reduction (Supplementary Figs. 21 and 22), and the selectivity of nitrite conversion to ammonia is near to 100%, which confirms the high selectivity of ammonia synthesis by np/ISAA-CuZn NO₂RR. ¹⁵N isotope labeling experiments further verify that the generated NH₃ originated from NO₂RR (Fig. 3f). The triple coupling peak representing ¹⁴NH₄⁺ was not detected in the ¹H NMR spectrum of the electrolyte after electrolysis, while a double peak for ¹⁵NH₄⁺ was observed. In addition, we further investigated the nitrite-reducing properties of np/ISAA-CuZn at ultralow nitrite concentrations (1 mM NO₂^‒). The np/ISAA-CuZn shows high selectivity toward NH₃ production from NO₂RR with a FE of 90.9 ± 2.6% at −0.5 V vs. RHE and a high yield rate of 3.3 ± 0.2 mg h^‒1 mg^‒1 at -0.7 V vs. RHE (Fig. 3g and Supplementary Fig. 23). Moreover, the evaluation of the performance of np/ISAA-CuZn at different nitrite concentrations indicates that it shows great potential for the conversion of NO₂^‒ wastewater to NH₃ over a wide range of concentrations (1 mM - 1 M) (Supplementary Fig. 24). Furthermore, using a two-electrode MEA electrolysis cell, np/ISAA-CuZn achieves excellent NO₂RR operational stability for 220 h at a high current density of 500 mA cm^‒2 and a stable ammonia FE of around 80% (Fig. 3h). Meanwhile, the NO₂^‒ removal rate is near 100%, and the NO₂^‒-N content in the treated solution is below the drinking water standard (DWS, NO₂^‒-N, 0.3 mg L^‒1) (Supplementary Fig. 25)²⁵. These results indicate that np/ISAA-CuZn has great potential for industrial applications. The relatively low NH₃ FE in the MEA electrolyzer compared to the FE values measured in the H cell could be attributed to the gradual decrease in nitrite concentration as the reaction proceeded, leading to an increase in competitive HER. Remarkably, scanning electron microscopy (SEM) and X-ray diffraction (XRD) characterizations show no detectable changes in the morphology and composition of np/ISAA-CuZn after MEA testing (Supplementary Fig. 26), The stability of NO₂RR electrolysis can be assigned to the stable structure resulting from the strong bonding between the isolated Cu and Zn atoms.

Investigation of NO₂RR electrosynthesis mechanism

To further explore the evolution dynamics of electronic structure and local atomic environment of np/ISAA-CuZn during the ammonia electrosynthesis process, in situ XAS measurements were performed with a homemade electrochemical cell (Supplementary Fig. 27)⁴⁰. During In situ XAS measurements, the applied potentials were first increased from open circuit voltage (OCV) to –0.3 and −0.5 V vs. RHE, and then decreased back to OCV. Figure 4a, b show the normalized Cu and Zn K-edge XANES at different operating potentials, respectively. As shown in the insets of Fig. 4a, b, the absorption edges of the K-edge XANES spectra of both Cu and Zn are shifted to the higher energy side under the OCV condition compared to the Ex-situ conditions, implying an increase in the oxidation state of Cu and Zn due to the adsorption of reactants on the active-sites^22,46. With the potential further decreased to –0.3 V vs. RHE and –0.5 V vs. RHE, the absorption edge of Cu and Zn K-edge XANES are shifted to the low-energy side, which can be assigned to ligand effects and dissociation of the reactants or reaction intermediates^35,47. The corresponding FT-EXAFS spectra further clarify the information of coordination structures in Fig. 4c, d. Notably, the potential change from OCV to –0.5 V vs. RHE, the scattering peaks of the Cu-Zn shells increases to ~2.13 Å from ~2.11 Å (insert of Fig. 4c), and the Cu-Zn bond length increases to ~2.25 Å from ~2.23 Å (insert of Fig. 4d), which may be related to the binding of isolated Cu-Zn active-sites to the intermediates^46,48. In contrast, no appreciable shifts in the absorption edge of the Cu K-edge XANES and the Cu-Cu scattering peaks of the FT-EXAFS of np/Cu were observed under different applied potentials (Supplementary Fig. 28). The different behavior further confirms that the isolated Cu and Zn atoms, as the synergistic active-sites, carrying strong electronic interactions under the operated bias voltages, which could promote adsorption and evolution of reactants during the reductive nitrite process. The unique porous structure of nanoporous materials can expose more active sites, providing sufficient surface sensitivity to obtain reliable in situ XAS data. However, the data sensitivity is still low compared to that of single-atom catalysts, and thus efforts are still needed in the structural design and synthesis of catalysts.

Fig. 4: In situ XAS and ATR-SEIRAS measurements of np/ISAA-CuZn at different applied potentials.

a, b In situ XANES spectra of np/ISAA-CuZn recorded at Cu K-edge (a) and Zn K-edge (b). c, d Cu K-edge (c) and Zn K-edge (d) FT-EXAFS spectra for np/ISAA-CuZn. e, f In situ ATR-SEIRAS spectra of the np/ISAA-CuZn (e) and np/Cu (f) in 0.2 M KHCO₃ + 10 mM KNO₂.

In situ ATR-SEIRAS was further performed to identify the reaction pathways and intermediates during the NO₂RR (Supplementary Fig. 29)¹⁷. Figure 4e shows the potential-dependent in situ ATR-SEIRAS spectra using np/ISAA-CuZn as the catalyst in the electrolyte containing KNO₂ (10 mM) and KHCO₃ (0.2 M). Obvious *NO₂ characteristic peaks in np/ISAA-CuZn are detected at OCV potential, which verified the strong adsorption of nitrite species by np/ISAA-CuZn⁴⁹. With increasing applied potentials from OCV to –0.2 V vs. RHE, the peak intensity of the characteristic peak located at ∼1211 cm^‒1 (*NO₂) is increased significantly, indicating that the *NO₂ is consumed in large quantities on the catalyst surface after applying the potential, corroborating that NO₂RR proceeds. Meanwhile, three characteristic peaks of hydrogenation intermediates (H-N-H at ∼1511 cm^‒1, N-H at ∼1164 and ∼3230 cm^‒1, and -NH₂ at ∼3363 cm^‒1), and produced NH₃ (NH₄⁺ at ∼1118 cm^‒1) are observed during the NO₂RR process, suggesting the efficient electroreduction of NO₂^‒ to generate plentiful hydrogenation intermediates for successive NH₃ electrosynthesis^50,51,52. In contrast, the characteristic peaks of hydrogenation intermediates and NH₃ in the in situ ATR-SEIRAS spectra of np-Cu were weak under different applied potentials (Fig. 4f), which implies that np-Cu has a weaker catalytic effect on the hydrogenation of nitrite species for producing NH₃, ultimately leading to poor NO₂RR performance. The results highlighted that np/ISAA-CuZn can optimize the adsorption of reactants and accelerating the protonation process, thus synergistically promoting selective NO₂^‒ to NH₃ electrocatalysis.

In general, the cathode is usually negatively charged at the reduction potential, leading to cation enrichment and anion depletion near the electrode, resulting in the formation of an electrical double layer (EDL)^53,54. When occurring in the vicinity of the electrode, the structure and composition of the EDL becomes more complex. Studying the adsorption process of reactants in EDL requires a combination of complex electrolyte factors (e.g., cations, solvents, anions, local pH, impurities, additives, and surface modifiers). It has been shown that disregarding the solvation effect and EDL can also provide an overview of thermodynamics⁵⁵. We focused on the effect of different Cu-Zn IMCs crystal structures on NO₂RR activity by DFT calculations (Supplementary Data 1), without considering the negative electrode potential and the resulting instantaneous EDL. Currently, there is no consensus on how to consider the first step of the NO_x^‒ adsorption mechanism due to the complexity of the EDL⁵⁶. Recent literatures have shown that there are two main processes regarding reactant adsorption: process 1. * + NO_x^‒ + H⁺ →*NO_X^‒ + (H + + e^‒); process 2. * + NOx^‒ + H+ →*HNO_x⁵⁶. Since the experimental solution is neutral, we consider the KNO₂ species as the adsorbent, and the adsorption process could be the co-adsorption of K and NO₂ on the catalyst surface to form *NO₂ intermediates (similar to process 1) (Fig. 5a). Figure 5a shows the NO₂RR pathway and free energies of each reaction state on Cu (111), CuZn₄, Cu₅Zn₈ and ISAA-CuZn (Supplementary Figs. 30–33). The first-step-hydrogenation of *NO₂ intermediate to *HNOO is a RDS for NO₂RR on CuZn IMCs. Benefiting from the isolating Cu-Zn sites in ISAA-CuZn, the ISAA-CuZn shows a Gibbs free energy (ΔG) of 0.18 eV during the protonation of *NO₂, which is much lower than that of CuZn₄ (0.53 eV) and Cu₅Zn₈ (0.45 eV). Notably, the first-step-hydrogenation of *NO₂ by Cu-Zn IMCs proceeds as follows: proton-electron pairs consisting of H⁺ and e^‒ attack the N-atoms of *NO₂ to form *HNOO instead of O-atoms to form *NOOH, which is markedly different from the case on the surface of pure Cu (111), suggesting that electronic interactions between the Cu and Zn site can alter the protonation of adsorbed species (Supplementary Fig. 34 and Supplementary Table 3). In addition. the charge density distributions of the ISAA-CuZn and Cu surfaces with different adsorbed species were visualized in Fig. 5b. The electron transfer of *HNOO (1.12 |e | ) is significantly higher than that of *NOOH (0.24 |e | ) on the ISAA-CuZn surface, while the opposite is true for the Cu surface (electron transfer of *HNOO and *NOOH is 0.31 |e| and 0.37 |e | , respectively). This indicates that isolated Cu-Zn active-sites are beneficial for protonation of *NO₂ intermediate species to *HNOO species rather than *NOOH species, which is intrinsic reason for the ΔG lowering of RDS.

Fig. 5: DFT calculations.

a Gibbs free energy diagram for NO₂RR on Cu, CuZn₄, Cu₅Zn₈ and ISAA-CuZn surfaces, insert: ΔG for different protonation steps on Cu, CuZn₄, Cu₅Zn₈ and ISAA-CuZn surfaces. b The charge density difference and bader charge analysis of different intermediate on Cu and ISAA-CuZn surfaces. The yellow and blue colors represent the spatial distribution with increased and decreased charge density, respectively. c Partial wave d-band centers difference (ε) of Cu and Zn atoms for CuZn₄, Cu₅Zn₈ and ISAA-CuZn. d The relationship between d_Cu-Zn, computational ε and ΔG of *NO₂ protonation.

Moreover, the partial wave d-band centers difference (ε) of Cu and Zn atoms is used as a descriptor for their electron interactions (Fig. 5c). The ISAA-CuZn exhibits the ε value of 4.00 eV, which is lower than that of Cu₅Zn₈ (4.18 eV) and CuZn₄ (4.27 eV). It is surprising that there is a strong linear scaling of the Cu-Zn atomic spacing between the ε value and the ΔG of *NO₂ hydrogenation for the Cu-Zn IMCs (Fig. 5d and Supplementary Fig. 35). These results point out that the Cu-Zn bond length (d_Cu-Zn) could be considered as a structural descriptor for defining the ε value and the ΔG of *NO₂ protonation, indicating that the ISAA-CuZn with the smallest d_Cu-Zn exhibits the strongest d-d electron interaction between Cu and Zn atoms, thereby reducing the ΔG of *NO₂ hydrogenation, and thus would deliver superior performance for the selective NO₂^‒ to NH₃ electrosynthesis. Furthermore, we calculated the adsorption and dissociation processes of water on the Cu and ISAA-CuZn surfaces (Supplementary Fig. 36), which provide the necessary *H for the protonation (hydrogenation) step of the *NO₂. The results show that the Zn site could effectively lower the hydrolysis dissociation barrier (0.28 eV), which provides sufficient protonic hydrogen for the reaction intermediate. This provides an important guarantee that ISAA-CuZn exhibits excellent NO₂RR activity.

Discussion

In summary, we synthesized a high-performance NO₂RR catalyst of nanoporous intermetallic single-atom alloy Cu-Zn, which enabled a remarkable neutral NO₂RR performance with an excellent NH₃ FE of 95% and the highest EE of ~59.1% in wide potential range from –0.2 to –0.8 V vs. RHE. The np/ISAA-CuZn catalyst further exhibited a remarkable 220 h operation stability at 500 mA cm^‒2 with a stable NH₃ FE of ~80% and a high NO₂^‒ removal rate of ~100% in MEA electrolyzers. The in situ XAS, ATR-SEIRAS, and DFT calculations revealed that the high activity of the np/ISAA-CuZn catalyst can be attributed to the strong electronic interactions between the isolated Cu-Zn active-sites altered the protonation adsorption species, effectively reduce the ΔG of *NO₂ intermediate hydrogenation for the rate-determining step, thus substantially enhancing NH₃ electroproduction. In addition, the Zn site can promote the adsorption/dissociation of H₂O and provide active hydrogen for the hydrogenation of N-containing intermediates to NH₃. This work suggests that the importance for rational design and manipulation of highly selective yet stable catalysts by atomically regulating the ordered active-site structure.

Methods

Synthesis of np/CuZn₄, np/Cu₅Zn₈, np/ISAA-CuZn, np/Cu

The pure Cu (99.9999%, Beijing Jiaming Platinum Nonferrous Metals Co., Ltd.) and pure Zn (99.995%, Beijing Jiaming Platinum Nonferrous Metals Co., Ltd.) were mixed in a certain ratio (The atomic percentages of Cu and Zn in the precursor alloys of np/CuZn₄, np/Cu₅Zn₈, np/ISAA-CuZn, and np/Cu were 6: 94, 15: 85, 15: 85 and 30: 70, respectively) and arc-melted (Ar atmosphere, 99.999%, Changsha Gaoke Gas Co.) to prepare Cu-Zn alloy ingots. The size of the precursor alloy ingot prepared by arc melting is φ10 mm × 8 mm. Subsequently, melt spinning technology was introduced to remelt the alloy ingot and quickly quenched on the surface of the spinning Cu roll at a rotation speed of 2 K rpm. Ribbons with dimensions ~30 μm thick, ∼2 mm wide, and ~10 cm long were achieved. The np/CuZn₅ was obtained by applying –1.36 Vs. Hg/HgO (Tianjin Aida Hengsheng Technology Development Co., Ltd.) in 1 M KOH (AR, Greagent) and keeping it for ~6.0 h. Then, for the preparation of np/CuZn₄, np/Cu₅Zn₈, np/ISAA-CuZn, electrochemical dealloying of the np/CuZn₅ ribbons was carried out using chronoamperometry in 1 M KOH solution at a constant voltage based on the LSV curve. The electrochemical dealloying potentials of np/CuZn₄, np/Cu₅Zn₈, np/ISAA-CuZn, and np/Cu were –1.26 V, –1.15 V, –0.95 V, and −0.50 V vs. Hg/HgO, and the corresponding dealloying time are ~3.2 h, ~4.0 h, ~3.0 h and ~1.3 h, respectively. The dealloyed samples were cleaned by deionized water and ethanol (GR, ≥99.8%, Greagent) more than three times and dried in a vacuum overnight.

Characterization

XRD patterns of the samples were taken by using a Rigaku MiniFlex X-ray diffraction. Microstructure and chemical composition were inspected with a MIR3 TESCAN SEM (at 10 kV and 8.5 mm work distance.) equipped with an Oxford energy dispersive X-ray spectroscopy. The transmission electron microscopy (TEM), HAADF-STEM and element mapping were taken by a Thermo scientific Themis Z (3.2) with double spherical aberration (Cs) correctors for both the probe-forming and image-forming objective lenses at an accelerating voltage of 300 kV. The contents of Cu and Zn were obtained via the ICP-OES (Thermofisher Scientific iCAP PRO X). Surface areas and porosity were tested on a JW-BK200C analyzer using Brunauer-Emmet-Teller (BET) adsorption-desorption isotherms at 77 K. XANES and Fourier transform (FT) curves of EXAFS spectrum were measured at beamline TLS 01C1 of Taiwan light source. The produced ammonia was quantified using ¹H nuclear magnetic resonance measurements (¹H NMR; Bruker Avance III HD-400). The ion-chromatography (IC) tests were performed by an LC-2010PLUS ion-chromatography system.

Preparation of the electrode

To prepare the catalyst ink, 10 mg of catalyst was ultrasonically dispersed in 1 mL of a solution (40 μL of Nafion solution (D520, 5 wt%, Dupont), 960 μL of ethanol, and ultrasonicated for 30 mins to form a uniform ink. 40 μL of a uniform ink dispersion was taken with a pipette, loaded onto the gas diffusion layer (1×1 cm², Sigraset 29 BC) electrode, and dried under ambient conditions. The loading of catalyst was estimated to be ~0.4 mg cm^‒2.

Electrochemical NO₂RR measurements

Electrochemical NO₂RR measurements were performed with an electrochemical workstation (lvium CompactStat.h20250). A typical three-electrode H-cell (Tianjin Aida Hengsheng Technology Development Co., Ltd.) was used, with a working electrode, an Ag/AgCl electrode (saturated KCl solution) (Tianjin Aida Hengsheng Technology Development Co., Ltd.) as the reference electrode, and a Pt plate counter electrode (Tianjin Aida Hengsheng Technology Development Co., Ltd.) in 0.2 M KHCO₃ + 10 mM KNO₂ (pH 8.2 ± 0.1) or 0.2 M KHCO₃ + 1 mM KNO₂ (pH 8.2 ± 0.1) electrolyte (KHCO₃: AR, Greagent; KNO₂: RG, Adamas). The reference electrode calibration was completed in H₂-saturated 1 M KOH at room temperature. The pH of the solution was determined when the displayed value was stable using a pH meter (PHS-2F, Leici). A volumetric flask was used to prepare a fresh electrolyte solution prior to testing. This was a cathode and an anode cell by a proton exchange membrane (Nafion117, 183μm, DuPont). The Nafion 117 membrane was boiled in H₂O₂ (5%) for 1 h and ultrapure water was boiled for 1 hour for pretreatment. It was then boiled in a 0.5 M H₂SO₄ solution for 1 h and rinsed several times in ultrapure water. The chronoamperometry tests were performed in a typical H-type cell that contains 30 mL electrolyte for each chamber. For the catalytic potential, we did not use iR correction. All electrochemical data (except stability testing) were repeated more than three times, with error bars representing the standard deviation of the data. All potentials were calibrated to the RHE by the following equation: E_RHE = E_Ag/AgCl + 0.197 + 0.0591 × pH (pH 8.2 ± 0.1).

MEA stability test. The experimental setup used for MEA electrolyzer stability testing was a customized MEA electrolyzer (0.5 cm^2, Shanghai Chuxi Industry Co.). The membrane electrode consisted of a cathodic (np/ISAA-CuZn ribbons, ~ 0.7 mm×0.7 mm×50 μm), a proton exchange membrane (Nafion117), and an anodic (IrO₂-Ti mesh), which were hot-pressed together (80 °C, 2 Mpa and 120 min). The volume of cathode and anode electrolytes was 2.5 L, and a flow rate of 10 mL min⁻¹.

Determination of ammonia

After diluting the post-test electrolyte to the appropriate concentration (to match the calibration curve range), the produced ammonia was determined spectrophotometrically by the modified indophenol blue method⁴³. 2 mL of the diluted electrolyte was taken and added sequentially to take 2 mL 1 M NaOH (GR, Greagent) solution containing 5 wt% salicylic acid (RG, Adamas) and 5 wt% sodium citrate dihydrate (AR, Greagent), 1 mL of 1 mL of 0.05 M NaClO (Active chlorine ≥7.5%, Greagent) solution and 0.2 mL of 1 wt% C₅FeN₆Na₂O (sodium nitroferricyanide, RG, 99%+, Adamas) solution²⁹. After standing at room temperature for 2 h, the absorption spectrum of the color-developing solution was measured using an ultraviolet-visible spectrophotometer (Shimadzu, UV-2600). The formation of indophenol blue was determined by absorbance at a fixed wavelength of 655 nm. The concentration-absorbance curves were calibrated using standard (NH4)₂SO₄ ( ≥ 99.5%, Greagent) solutions.

Determination of nitrite

The NO₂^‒ in solution was quantified spectrophotometrically by N-(1-naphthyl)-ethylenediamine dihydrochloride⁵⁷. Typically, ultrapure water (90 mL) and acetic acid (5 mL, GR, Greagent) are mixed with N-(1-naphthyl)-ethylenediamine dihydrochloride (5 mg, RG, Adamas) and p-aminobenzenesulfonamide (0.5 g, RG, Adamas) to obtain the color reagent. The tested electrolyte solution was diluted to the appropriate concentration to be within the detection range; 1 mL of the treated electrolyte was mixed with 4 mL of the color developer, mixed homogeneously, and aged for 15 minutes before monitoring the absorbance at 540 nm. The concentration-absorbance curves were calibrated using standard ammonia sulfate solutions. The concentration-absorbance curves were calibrated using standard KNO₂ solutions.

Determination of gaseous products

Detection and quantification of the gaseous products were carried out by a gas chromatograph (GC) equipped with a flame ionization detector (FID) and a thermal conductivity detector (TCD), which uses high-purity argon (99.999%) as carrier gas³⁵.

Calculation of faradaic efficiency

The Faradic efficiency for NH₃ was calculated as follows:

$${{\rm{Faradaic\; efficiency}}}(\%)=({nFcV})/Q\times 100$$

(1)

where n is the electron-transfer number, F is the Faraday constant (96,485 C mol⁻¹), c is the concentration of NH₃ produced, V is the volume of the catholyte of the cathode chamber, and Q represents the applied overall coulomb quantity.

The Faradaic efficiency of each gas product was calculated by the equation:

$${{\rm{Faradaic\; efficiency}}}(\%)=({nFxV})/j*100$$

(2)

where n is the number of electrons transferred, F is Faraday constant (96,485 C mol^–1), x is the mole fraction of product, V is the total molar flow rate of gas and j is the total current.

Calculation of yield rate

The average yield rate was calculated as follows:

$$v=(c\times V)/(t\times m)$$

(3)

where c is corresponding product concentration, V is the total volume of electrolyte, t is time for electrocatalysis and m is the catalyst loadings.

Calculation of energy efficiency

The energy efficiency was defined as the ratio of fuel energy to applied electrical power, which was calculated by

$${{EE}}_{{NH}3}=(({E}^{\theta }{OER}-{{E}^{\theta }}_{{NH}3})\times {{FE}}_{{NH}3})/({E}_{{OER}}-{E}_{{NH}3})$$

(4)

where E^θ_NH3 represents the equilibrium potential of nitrite electroreduction to NH₃, E^θ_OER is the equilibrium potential of the oxygen evolution reaction (OER), FE_NH3 is the Faradaic efficiency for NH₃, and E_OER and E_NH3 are the applied potentials.

In situ XAS measurements

In situ XAS tests were performed in fluorescence mode at the NSRRC TLS 01C1 beamline. The experimental setup consisted of an electrochemical workstation, a homemade cell, and a three-electrode system (working electrode (prepared by coating a carbon paper with catalyst), a carbon rod counter electrode, and a Ag/AgCl reference electrode). The electrolyte solution was 0.2 M KHCO₃ + 10 mM KNO₂. The XAS data obtained were processed by the ATHENA software.

In situ ATR-SEIRAS experiments

Electrochemical in situ ATR-SEIRAS measurements were performed in internal reflection mode on a Thermo Fisher Nicolet iS50 (equipped with an ElectroChemIR unit from Pike Technologies). The experiments were carried out in a three-electrode system: working electrode (prepared by coating catalyst on monocrystalline silicon loaded with a gold film), counter electrode (platinum wire) and reference electrode (Ag/AgCl electrode). The electrolyte solution was 0.2 M KHCO₃ + 10 mM KNO₂ solution. All spectra were collected at a spectral resolution of 4 cm^‒1 and expressed in transmittance units, with a negative and positive peak indicating an increase and decrease in interfacial species, respectively.

Computational methods

DFT calculations were performed using the Vienna Ab-initio Simulation Package (VASP 5.4.4), with the Perdew-Burke-Ernzerhof exchange-correlation functional of generalized gradient approximation^58,59. The basis set utilized projector-augmented-wave pseudopotential method, and the energy cutoff was set at 400 eV^60,61. Convergence was assumed when forces on each atom was less than 0.02 eV/Å and the self-consistent field tolerance was 10^‒5eV in the geometry optimization. The DFT-D3 method with Grimme’s scheme was employed to correct the van der Waals interactions⁶².

In our calculations, the pure Cu surface was modeled by four-layer (111) fcc slabs with a 4 × 4 supercell, and a 3 × 3 supercell of CuZn (110) with four atomic layers was considered for the ISAA-CuZn. The CuZn₄ presents a disordered solid solution phase and its crystal structure is similar with pure Zn. Thus, we first established a four-layer pure Zn (0001) hcp slabs using 4 × 4 supercells, totaling 64 atoms of Zn. We then randomly replaced 13 of these atoms to construct 50 initial structures and optimized these structures to obtain stable model of np/CuZn₄. For the Brillouin zone integration, a Monkhorst-Pack k-point mesh of 3 × 3 × 1 was employed in these calculations. Moreover, a 1 × 1 unit cell of Cu₅Zn₈ (110) with six atomic layers was considered that the Monkhorst-Pack k-point sampling in the Brillouin zone was set to a 3 × 2 × 1 for calculations. Here, the top two atomic layers were relaxed, and all the atomic layers at the bottom were frozen. To avoid the interactions between periodic structure, the vacuum space of 20 Å was employed along the z direction.

As an indicator for each elemental step of NO₂RR, the G is calculated by

$$G=E+{E}_{{ZPE}}+\int {C}_{p}{dT}-{TS}$$

(5)

where $E$ is the DFT-optimized total energy, ${E}_{{ZPE}}$ is the zero-point vibrational energy, ${C}_{p}$ is the heat capacity, $T$ = 298.15 K is the temperature and $S$ is the entropy. The zero-point vibrational energies, internal energy and entropies of the adsorbates were computed from vibrational frequency calculations, in which only the adsorbate vibrational modes were computed explicitly, while the catalyst was fixed⁶³. All corrections of G were obtained using VASPKIT (v.1.1.2) software⁶⁴.

The calculation of reaction free energy (G) is based on the computational hydrogen model (CHE) proposed by Nørskov as following⁶⁵:

$$({{{\rm{H}}}}^{+}+{{{\rm{e}}}}^{-})\to \frac{1}{2}{{{\rm{H}}}}_{2}$$

(5)

Transition states (TS) were located using the climbing-image nudged elastic band (CI-NEB) method with the quasi-Newton algorithm⁶⁶.