Introduction

At the mid-latitudes, sea surface temperature anomaly (SSTA) at spatial scales of O(1000 km) or larger, referred to as the large-scale SSTA henceforth, is primarily driven by atmospheric internal variabilities1. Once generated, the SSTA induces surface heat flux anomaly (SHFA) that, in turn, acts to damp itself. This process, known as the surface heat flux feedback, serves as a pivotal element in the coupled ocean-atmosphere system1,2,3. It not only regulates the amplitude, persistence and predictability of SSTA1,3,4,5,6 but also exerts broad effects on many aspects including the stability of global overturning circulation7,8,9, the variability of major climate modes10,11,12,13,14 and the climatic response to stratospheric ozone forcing15.

The intensity of the surface heat flux feedback α, defined as the surface heat flux change in response to 1 K SST change, varies considerably with space, season, and spatial scale5,6,8,16,17,18,19,20,21,22. Such variations reflect the complicated underlying dynamics of the surface heat flux feedback. On the one hand, the value of α depends on the mean-state SST due to the nonlinearity in the Clausius–Clapeyron relation (i.e., the nonlinear dependence of the saturated specific humidity on temperature)22 and on the near-surface atmosphere condition, especially the wind speed5,6,20,22. Specifically, higher mean-state SST and wind speed promote the SHFA induced by SSTA, increasing the value of α. On the other hand, the value of α is affected by the adjustment of the marine atmospheric boundary layer (MABL) to underlying SSTA6,19,20,22. The adjustment manifests in many aspects, including the near-surface air conditions5,6,22,23,24,25,26,27,28,29,30, the stability and thickness of MABL24,29,30 as well as the rainfall29. In particular, the adjustment of near-surface air temperature and humidity to underlying SSTA diminishes the air-sea thermal disequilibrium. This tends to weaken SHFA caused by SSTA, reducing the value of α.

Increased greenhouse gas emission has been exerting profound impacts on the midlatitude ocean and atmosphere, including warmer mean-state SST31,32, strengthened surface zonal wind33, and more stable MABL34. Such changes may reinforce or counteract each other in terms of the surface heat flux feedback, complicating its response to greenhouse gas-induced warming. So far, it remains elusive how the midlatitude surface heat flux feedback for large-scale SSTA will change in the future. Here, we address this question using outputs from an ensemble of global climate models in the Coupled Model Intercomparison Project Phase 6 (CMIP6)35.

Results

Simulated surface heat flux feedback in the CMIP6

We first validate the simulated midlatitude surface heat flux feedback for large-scale SSTA in the CMIP6 models (Supplementary Table 1) against that in the reanalysis dataset (‘CMIP6 models and reanalysis dataset’ and ‘Computation of large-scale SSTA and SHFA’ in Methods). Fig. 1 compares the time-mean (1950–1999) α and its decomposition into turbulent and radiative components (αT and αR) in the CMIP6 with their counterparts in the reanalysis dataset (‘Computation of surface heat flux feedback’ in “Methods”). The value of α in the reanalysis dataset is positive across the midlatitudes (20°–50°) and dominated by \({\alpha }_{T}\). It shows a general negative trend with the increasing latitude (Supplementary Fig. 1), with local enhancement along the major subtropical western boundary currents as well as their extensions (WBCEs). Such a spatial pattern of α is similar to that of mean-state SST and partially due to the nonlinearity in the Clausius–Clapeyron relation22,36.

Fig. 1: Comparison of midlatitude large-scale surface heat flux feedback in the ERA5 reanalysis and Coupled Model Intercomparison Project Phase 6 (CMIP6) during 1950-1999.
figure 1

a–c, Spatial distribution of surface heat flux feedback (a) and its decomposition into turbulent (b) and radiative (c) components in the ERA5 reanalysis dataset. d–f, Same as (a–c), but for the multi-model ensemble (MME) mean of CMIP6. Regions within 20° S–20° N are excluded from analysis and filled with black oblique lines.

Full size image

The multi-model ensemble (MME) mean of CMIP6 reproduces the magnitude of α in the reanalysis dataset reasonably well (Fig. 1). The spatial mean α at the midlatitudes is 16.0 \({{{\rm{W}}}}\cdot {{{{\rm{m}}}}}^{-2}\cdot {{{{\rm{K}}}}}^{-1}\) in the CMIP6, very close to 16.1 \({{{\rm{W}}}}\cdot {{{{\rm{m}}}}}^{-2}\cdot {{{{\rm{K}}}}}^{-1}\) in the reanalysis dataset. The spatial pattern of α in the CMIP6 shows broad agreement with that in the reanalysis, qualitatively capturing the negative trend of α with the latitudes (Supplementary Fig. 1) and locally enhanced α along the subtropical WBCEs. However, the CMIP6 fails to faithfully reproduce some regional structures of α in the reanalysis dataset, leading to a moderate correlation coefficient (0.52) between the spatial variations of α in the CMIP6 and the reanalysis dataset. It should be noted that such regional differences of α are not necessarily attributed to the deficiencies of CMIP6 models but may partially result from the uncertainties of the reanalysis dataset itself, such as the lack of observational constraint37. In summary, the simulated α in the CMIP6 is qualitatively consistent with that in the reanalysis, whereas quantitative differences do exist in some regions. In view of these regional differences, we will mainly focus on the spatially overall change of α under greenhouse gas-induced warming.

Response of surface heat flux feedback to greenhouse gas-induced warming

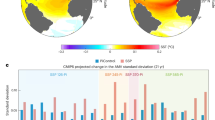
Under a high radiative forcing scenario, the projected surface heat flux feedback for large-scale SSTA in the CMIP6 is universally weakened across the midlatitudes (Fig. 2d–f), compared to its pre-industrial level (Fig. 2a–c). The MME mean α in the CMIP6 averaged over 20°–50° during 2051–2100 is only about 52% of that in the pre-industrial control (PI-CTRL) simulation (Fig. 2g, h). This decrease of α is primarily attributed to the reduced \({\alpha }_{T}\) with the change of \({\alpha }_{R}\) playing a secondary role (Fig. 2g, h). We remark that the decrease of α under greenhouse gas-induced warming holds for not only the MME mean of CMIP6 but also its individual members (Supplementary Fig. 2). Such inter-model consistency lends strong support to the fidelity of the projected weakening of surface heat flux feedback for large-scale SSTA at midlatitudes.

Fig. 2: Projected changes of midlatitude large-scale surface heat flux feedback under greenhouse gas-induced warming.
figure 2

a–c, Spatial distribution of time-mean surface heat flux feedback (a) and its decomposition into turbulent (b) and radiative (c) components in the pre-industrial control (PI-CTRL) simulation. d–f, Same as (a–c), but for the difference between the SSP585 simulation (2051–2100) and the PI-CTRL simulation. Regions within 20°S-20°N are excluded from analysis and filled with black oblique lines. Black dots mark the regions where the change of the surface heat flux feedback is statistically insignificant at the 95% confidence level. g, h, show the spatial mean values of (a–c) and (d–f), respectively. All the results shown here are the multi-model ensemble (MME) mean of Coupled Model Intercomparison Project Phase 6 (CMIP6) with error bars in (g) and (h) denoting the 95% confidence intervals of MME mean.

Full size image

To unravel the underlying mechanisms for the reduction \({\alpha }_{T}\) under greenhouse gas-induced warming, we decompose \({\alpha }_{T}\) into the components related to the background air-sea state \({\alpha }_{T}^{B}\) and adjustment of MABL to underlying SSTA \({\alpha }_{T}^{A}\) (‘Decomposition of surface turbulent heat flux feedback’ in “Methods”). The former assumes an atmosphere completely unaffected by the underlying SSTA, in other words, possessing an infinitely large heat capacity and ability to hold water vapor. The \({\alpha }_{T}\) in the PI-CTRL simulation is systematically lower than \({\alpha }_{T}^{B}\) (Fig. 3a and Supplementary Fig. 3). This is because the MABL inevitably adjusts to SSTA in reality23,25,27,28. On the one hand, the adjustments of near-surface air temperature and specific humidity, referred to as the thermodynamic adjustments and denoted as \({\alpha }_{T}^{{TA}}\), diminish the air-sea thermal disequilibrium caused by SSTA and thus weaken the surface heat flux feedback. The \({\alpha }_{T}^{{TA}}\) largely reconciles the difference between \({\alpha }_{T}\) and \({\alpha }_{T}^{B}\) in the PI-CTRL simulation (Fig. 3a). On the other hand, the adjustment of near-surface wind speed, referred to as the dynamic adjustment and denoted as \({\alpha }_{T}^{{DA}}\), contributes negligibly to the \({\alpha }_{T}\) in the PI-CTRL simulation (Fig. 3a). Under greenhouse gas-induced warming, \({\alpha }_{T}^{B}\) is increased, whereas \({\alpha }_{T}^{{TA}}\) becomes more negative (Fig.3d). The change of \({\alpha }_{T}^{{TA}}\) is larger in magnitude than that of \({\alpha }_{T}^{B}\), accounting for the reduced \({\alpha }_{T}\) under greenhouse gas-induced warming. Again, the change of \({\alpha }_{T}^{{DA}}\) plays a negligible role. In summary, the weakened midlatitude surface heat flux feedback for large-scale SSTA under greenhouse gas-induced warming is primarily attributed to the stronger thermodynamic adjustment of MABL to underlying SSTA.

Fig. 3: Factors responsible for the weakened midlatitude large-scale surface turbulent heat flux feedback under greenhouse gas-induced warming.
figure 3

a Spatial mean large-scale surface turbulent heat flux feedback and its decomposition into the components related to the background air-sea state \({\alpha }_{T}^{B}\), thermodynamic adjustment \({\alpha }_{T}^{{TA}}\), dynamic adjustment \({\alpha }_{T}^{{DA}}\), and the residue term in the pre-industrial control (PI-CTRL) simulation. b, and (c), Same as a, but for the surface latent and sensible turbulent heat flux only, respectively. d–f Same as (a–c), but for the difference between the SSP585 simulation (2051–2100) and the PI-CTRL simulation. All the results shown here are the multi-model ensemble (MME) mean of Coupled Model Intercomparison Project Phase 6 (CMIP6) with the error bars denoting its 95% confidence interval.

Full size image

The increased \({\alpha }_{T}^{B}\) under greenhouse gas-induced warming is mostly attributed to the latent heat flux component (Fig. 3d–f) and can be understood based on the nonlinearity in the Clausius–Clapeyron relation22,36. For a given magnitude of SSTA, the latent heat flux anomaly it induces is proportional to the derivative of saturated specific humidity with respect to the mean-state SST (‘Decomposition of surface turbulent heat flux feedback’ in “Methods”). As this derivative is an increasing function of mean-state SST due to the nonlinear Clausius–Clapeyron relation22,36 (Supplementary Fig. 4), the warmer mean-state SST under greenhouse gas-induced warming leads to a stronger response of latent heat flux anomaly to underlying SSTA, accounting for the increased \({\alpha }_{T}^{B}\). This is argument is further supported by a positive trend of \({\alpha }_{T}^{B}\) overtime in the ERA reanalysis (Supplementary Fig. 5), as the mean-state SST increase has already emerged during the past several decades38.

The stronger thermodynamic adjustment of MABL to underlying SSTA may result from the enhanced MABL stability that inhibits the removal of SSTA’s imprints on the near-surface air temperature and specific humidity via vertical mixing29,39,40,41. To test this conjecture, we analyze the inter-model relationship between the projected change of MABL stability and the change of thermodynamic adjustment of MABL to underlying SSTA. The MABL stability is measured as the air temperature at the 850hPa minus that at the 1000hPa. The thermodynamic adjustment of MABL to underlying SSTA is separately measured as the derivative of near-surface air temperature and specific humidity anomalies with respect to the underlying SSTA. Under greenhouse gas-induced warming, all the CMIP6 models consistently project a more stable MABL at midlatitudes (Fig. 4), probably due to the decreased moist-adiabatic lapse rate42. However, there are pronounced quantitative differences in the projected MABL stability changes among models. These inter-model differences are tightly correlated to the inter-model differences in the projected changes of thermodynamic adjustment of MABL to underlying SSTA (Fig. 4). The above results lend support that the enhanced MABL stability under greenhouse gas-induced warming is primarily responsible for the stronger thermodynamic adjustment of MABL to underlying SSTA.

Fig. 4: Underlying mechanisms for the stronger thermodynamic adjustment of the marine atmospheric boundary layer (MABL) to underlying large-scale sea surface temperature anomaly (SSTA) under greenhouse gas-induced warming.
figure 4

Scatterplot of MABL stability change vs. thermodynamic adjustment change of MABL in the individual Coupled Model Intercomparison Project Phase 6 (CMIP6) members. The MABL stability is computed as the difference in air temperature between 850hPa and 1000hPa. The thermodynamic adjustment of MABL to underlying SSTA is computed as the derivative of near-surface air temperature anomaly (a) and specific humidity anomaly (b) with respect to SSTA. These quantities are first averaged over the midlatitudes in the pre-industrial control (PI-CTRL) simulation and then subtracted from their counterparts during 2051–2100 in the SSP585 simulation to compute the changes under greenhouse gas-induced warming. The linear fit (solid black line) is shown together with the correlation coefficient r and corresponding p-value.

Full size image

Discussion

This study reveals the significant weakening of midlatitude large-scale surface heat flux feedback in a warming climate due to the more stabilized MABL, providing insight into the response of large-scale air-sea interactions to greenhouse gas-induced warming. As the surface heat flux feedback acts as a major damping mechanism for large-scale SSTA at midlatitudes2,43, its weakening is likely to increase the SSTA variance. This conjecture seems to be supported by the significantly increased frequency spectral level of midlatitude large-scale SSTA under greenhouse gas-induced warming (Fig. 5a, d). The spectral level during 2051–2100 is 10%–25% higher than that in the PI-CTRL simulation at sub-seasonal to interannual time scales.

Fig. 5: Effects of weakened surface heat flux feedback on the midlatitude large-scale sea surface temperature anomaly (SSTA) variance under greenhouse gas-induced warming.
figure 5

Frequency spectra of large-scale SSTA (a), normalized forcing surface heat flux anomaly (SHFA) (b), and normalized damping SHFA (c) averaged over the midlatitudes in the pre-industrial control (PI-CTRL) simulation. d–f, Same as, (a–c), but for their percentage changes under greenhouse gas-induced warming (2051–2100) relative to the pre-industrial levels. The decomposition of SHFA into the forcing and damping components is described in ‘Computation of surface heat flux feedback’ in Methods. Once the forcing and damping SHFAs are obtained, they are normalized by the heat capacity of the ocean surface mixed layer. Lines and shadings correspond to the multi-model ensemble (MME) mean of Coupled Model Intercomparison Project Phase 6 (CMIP6) and its 95% confidence interval.

Full size image

It should be noted that the enhanced mid-latitude large-scale SSTA variance could result from multiple factors. The decreased ocean surface mixed layer depth in a warming climate (Supplementary Fig. 6a) reduces the heat capacity of the ocean surface mixed layer, acting to amplify the response of SST to atmospheric internal forcing and enlarge its variance44. In fact, such an effect has been argued to contribute to the stronger SST seasonal cycle under greenhouse gas-induced warming45,46,47,48. To demonstrate that the enhanced SSTA variance under greenhouse gas-induced warming is primarily due to the weakened surface heat flux feedback rather than the shoaled ocean surface mixed layer (note that our definition of SSTA excludes the SST seasonal cycle), we decompose the SHFA into the forcing and damping components, denoted as the forcing SHFA and damping SHFA, respectively (‘Computation of surface heat flux feedback’ in “Methods”). The forcing and damping SHFAs are normalized by the heat capacity of the ocean surface mixed layer to quantify their effects on SSTA variations. The ocean surface mixed layer depth (MLD) is computed as the depth where the potential density is 0.03 kg m−3 denser than its surface value49. The time-mean MLD during 2051–2100 and PI-CTRL simulation are used to normalize the SHFA in these two periods, respectively.

There is no significant change for the frequency spectrum of normalized forcing SHFA under greenhouse gas-induced warming (Fig. 5b, e), although the shoaled ocean surface mixed layer alone would lead to an intensification of the normalized forcing SHFA variance. This is because the SHFA generated by atmospheric internal variability (i.e., the unnormalized forcing SHFA) weakens in a warming climate and largely offsets the effect of decreased ocean surface mixed layer depth on the normalized forcing SHFA (Supplementary Fig. 6b, c). In contrast, the frequency spectrum of normalized damping SHFA shows a significant reduction at sub-seasonal to interannual time scales under greenhouse gas-induced warming (Fig. 5c, f), as the weakened surface heat flux feedback overwhelms the shoaled ocean surface mixed layer in terms of their effects on the normalized damping SHFA. Therefore, the enhanced variance of midlatitude large-scale SSTA under greenhouse gas-induced warming is primarily caused by the weakened surface heat flux feedback.

In addition to the SSTA variance, the surface heat flux feedback has been demonstrated to exert evident influences on the stability of global overturning circulation7,8,9. Weaker surface heat flux feedback generally gives rise to stronger model resistance to freshwater perturbation9, which may alleviate the slowdown of global overturning circulation caused by surface freshening of subpolar North Atlantic under greenhouse gas-induced warming50,51. Moreover, there is some evidence that weakened surface heat flux feedback at the midlatitudes could decrease the amplitude of the North Atlantic Oscillation (NAO) at interannual and longer timescales10,14. As climate simulations project intensified NAO in a warming climate52, the weakened surface heat flux feedback is supposed to exert a counteracting effect on the projected NAO intensification.

Finally, there are two limitations of our study. First, the large-scale SSTA and SHFA should involve processes at a wide range of time scales. However, only those at monthly-to-decadal time scales are taken into consideration in this study due to the temporal resolution and coverage of the CMIP6 model data and the way the anomalies are computed (‘CMIP6 models and reanalysis dataset’ and ‘Computation of large-scale SSTA and SHFA’ in “Methods”). Second, this study excludes the surface heat flux feedback at the tropics, because the strong air-sea coupling there makes it difficult to isolate the SHFA induced by SSTA from that induced by atmospheric internal variabilities2,16,19. In view of the important role of surface heat flux feedback in the climate system, it is imperative to have a comprehensive knowledge of the anthropogenic changes of the surface heat flux feedback for SSTA at various spatio-temporal scales across the global ocean.

Methods

CMIP6 models and reanalysis dataset

To analyze the response of surface heat flux feedback to greenhouse gas-induced warming, we use monthly outputs from a selected subset of CMIP6 models (Supplementary Table 1). Specifically, we select models that consists of a 500-year-long PI-CTRL simulation and a historical-and-future transient (HF-TNST) simulation from 1850 to 2100, outputting all the necessary quantities for the computation of surface heat flux feedback and its decomposition into different components (‘Decomposition of surface turbulent heat flux feedback’ in “Methods”).

The PI-CTRL simulation is driven by the pre-industrial natural variability forcing without impacts from anthropogenic greenhouse gas. The HF-TNST simulation, initialized from the PI-CTRL simulation, adopts the historical forcing during 1850–2014 and shared socioeconomic pathway 5–8.5 (SSP585) greenhouse gas forcing during 2015–210035. For the CMIP6 models containing an ensemble of PI-CTRL and HF-TNST simulation members, only the first ensemble member is used. The model outputs during the last 50 years in the PI-CTRL simulation and during the years 2051–2100 in the HF-TNST simulation are used to compute the surface heat flux feedback in the pre-industrial and high radiative forcing scenarios, respectively. As the CMIP6 models differ in their native grids, all the model outputs are interpolated onto a uniform 1° × 1° grid to facilitate the computation of the MME mean of CMIP6. To evaluate the fidelity of CMIP6 models in simulating the surface heat flux feedback, we use the monthly ERA5 reanalysis dataset spanning from 1940–202037 and compare the surface heat flux feedback derived from the CMIP6 models and ERA5 reanalysis.

Computation of large-scale SSTA and SHFA

At midlatitudes, the air-sea interactions at oceanic mesoscales and large scales differ fundamentally from each other30,53,54,55,56. In particular, the large-scale and mesoscale SSTAs are driven primarily by atmospheric and oceanic internal variabilities, respectively. Although understanding the anthropogenic change of mesoscale air-sea interaction is important for its own sake57, this study focuses on the response of large-scale air-sea interactions to greenhouse gas-induced warming. The large-scale SSTA and SHFA are computed according to the following steps. First, we select a period for analysis, e.g., the last 50 years in the PI-CTRL simulation or 2051–2100 in the HF-TNST simulation. Second, the monthly SST and SHF are subtracted by their respective monthly climatology over the selected period to obtain the anomalies (SSTA and SHFA). Third, a 4° × 4° running mean is applied to the SSTA and SHFA to filter out the mesoscale signals. The cutoff wavelength of the 4° × 4° running mean is around O(1000 km), comparable to the outer range of wavelength of oceanic mesoscale eddies at midlatitudes58. Fourth, linear trends and ENSO signals are removed from SSTA and SHFA at each grid59. We remove the ENSO’s imprints on the SSTA and SHFA as these imprints are characterized by strong air-sea coupling, making it difficult to disentangle SHFA induced by SSTA and atmospheric internal variabilities2,16,60. This is done by regressing SSTA and SHFA at each grid onto the first two principal components of SSTA in the tropical Pacific within 12.5°S-12.5°N and then subtracting the regression lines from SSTA and SHFA at each grid59. Imprints of ENSO signals on the other model outputs, such as near-surface air temperature, are removed in the same way. We remark that the removal of ENSO signals leads to a slight decrease in the variances of SSTA and SHFA at the midlatitudes, consistent with the global ENSO teleconnections61,62,63. Nevertheless, removing ENSO signals or not does not affect the major conclusions of this study, i.e., weakened surface heat flux feedback under greenhouse-gas-induced warming (Supplementary Fig. 7).

Supplementary Fig. 8b shows the spatial distribution of the correlation coefficient between large-scale SSTA tendency and turbulent heat flux anomaly (THFA) for the MME mean of CMIP6. Consistent with an atmosphere-driven regime, the correlation coefficient is highly positive. In addition, varying the filter size from 2° to 6° does not affect the correlation coefficient substantially (Supplementary Fig. 8). This is partially because oceanic mesoscale signals are largely suppressed in the monthly mean CMIP6 model output.

Computation of surface heat flux feedback

The SHFA at some locations can be decomposed as 1,2,

$${Q}^{{\prime} }={q}^{{\prime} }-\alpha {T}^{{\prime} }$$
(1)

where the primes denote the anomalies, \({q}^{{\prime} }\) is the SHFA component that is attributed to atmospheric internal variability and acts to generate SSTA (\({T}^{{\prime} }\)), and \(-\alpha {T}^{{\prime} }\) the SHFA component induced by \({T}^{{\prime} }\) with the coefficient \(\alpha\) quantifying the surface heat flux feedback.

The value of \(\alpha\) can be estimated based on the cross-covariance between \(T{\prime}\) and \(Q{\prime}\), expressed as 16,19

$${R}_{{TQ}}\left(\tau \right)={R}_{{Tq}}\left(\tau \right)-\alpha {R}_{{TT}}\left(\tau \right)$$
(2)

where \({R}_{{TQ}}\left(\tau \right)\) (\({R}_{{Tq}}\left(\tau \right)\)) is the cross-covariance between \({T}^{{\prime} }\) and \({Q}^{{\prime} }\) (\({q}^{{\prime} }\)) when \({Q}^{{\prime} }\) (\(q{\prime}\)) leads \(T{\prime}\) by \(\tau\) months and \({R}_{{TT}}(\tau )\) is the auto-covariance of \({T}^{{\prime} }\) at \(\tau\)-month lag.

At the mid-latitudes, \({R}_{{Tq}}(\tau )\) becomes negligible when \(T^{\prime}\) leads \(Q^{\prime}\) by a month or longer due to the short persistence of atmospheric internal variabilities1,2,16,19, in which case the value of \(\alpha\) can be approximated as

$$\alpha=-\frac{d{Q}^{{\prime} }}{d{T}^{{\prime} }}\approx -\frac{{R}_{{TQ}}\left(\tau \right)}{{R}_{{TT}}\left(\tau \right)}$$
(3)

The value of \(\alpha\) is computed by averaging the values of Eq. (3) at \(\tau=-1,\,-2,\,-3\) (Park et al. 6). To avoid singularity caused by zero \({R}_{{TT}}\left(\tau \right)\), we exclude samples with \({R}_{{TT}}\left(\tau \right)\) insignificant from zero at the 95% confidence level before computing the average16. Once \(\alpha\) is obtained, the SHFA component induced by \({T}^{{\prime} }\) (the damping SHFA) is computed as \(-\alpha {T}^{{\prime} }\) and the SHFA component attributed to atmospheric internal variability (the forcing SHFA) is computed as the difference between \(Q^{\prime}\) and \(-\alpha {T}^{{\prime} }\) according to Eq. (1).

Decomposition of surface turbulent heat flux feedback

The surface heat flux \(Q\) is the sum of surface turbulent (\({Q}_{T}\)) and radiative heat flux (\({Q}_{R}\))

$$Q={Q}_{T}+{Q}_{R},$$
(4)

where \({Q}_{T}\) is the sum of sensible (\({Q}_{S}\)) and latent (\({Q}_{L}\)) components expressed as:

$${Q}_{S}=\rho U{C}_{S}{C}_{p}\left({T}_{a}-T\right)$$
(5)
$${Q}_{L}=\rho U{C}_{L}L\left({q-q}_{{sat}}\right)$$
(6)

where \(\rho\), \({T}_{a}\), and \(q\) are the 2-m air density, temperature, and specific humidity\(,\,{q}_{{sat}}\) is the saturated specific humidity at \(T\), \(U\) is the 10-m wind speed, \({C}_{p}\) is the air specific heat capacity, \(L\) is the latent heat of vaporization, and \({C}_{S}\) and \({C}_{L}\) are the transfer coefficients for sensible and latent heat. Decompose the quantities in Eqs. (5) and (6) into the climatological mean values and anomalies (denoted with the overbars and primes, respectively). Linearizing Eqs. (5) and (6) with respect to anomalous quantities gives rise to

$${{Q}_{S}}^{{\prime} }\approx \bar{\rho }\bar{U}{\bar{C}}_{S}{\bar{C}}_{p}\left({{T}_{a}}^{{\prime} }-{T}^{{\prime} }\right)+\bar{\rho }{\bar{C}}_{S}{\bar{C}}_{p}\left(\bar{T}-{\bar{T}}_{a}\right){\cdot U}^{{\prime} }$$
(7)
$${{Q}_{L}}^{{\prime} }\approx \bar{\rho }\bar{U}{\bar{C}}_{L}\bar{L}\left({q}^{{\prime} }-\frac{d{\bar{q}}_{{sat}}}{d\bar{T}}{T}^{{\prime} }\right)+\bar{\rho }{\bar{C}}_{L}\bar{L}{\left({\bar{q}}_{{sat}}-\bar{q}\right)\cdot U}^{{\prime} }$$
(8)

where we have approximated \(\rho\), \({C}_{p}\), \(L\), \({C}_{S}\) and \({C}_{L}\) as their climatological mean values, and \({\bar{q}}_{{sat}}={q}_{{sat}}(\bar{T})\). Taking the derivative of Eqs. (7) and (8) with respect to \(T{\prime}\) and adding them up lead to the expression of \({\alpha }_{T}\)

$${\alpha }_{T}= \bar{\rho }\bar{U}{\bar{C}}_{S}{\bar{C}}_{p}-\bar{\rho }\bar{U}{\bar{C}}_{S}{\bar{C}}_{p}\frac{d{{T}_{a}}^{{\prime} }}{d{T}^{{\prime} }}+\bar{\rho }{\bar{C}}_{S}{\bar{C}}_{p}\left(\bar{T}-{\bar{T}}_{a}\right)\frac{d{U}^{{\prime} }}{d{T}^{{\prime} }}\\ +\bar{\rho }\bar{U}{\bar{C}}_{L}\bar{L}\frac{d{\bar{q}}_{{sat}}}{d\bar{T}}-\bar{\rho }\bar{U}{\bar{C}}_{L}\bar{L}\frac{d{q}^{{\prime} }}{d{T}^{{\prime} }}+\bar{\rho }{\bar{C}}_{L}\bar{L}\left({\bar{q}}_{{sat}}-\bar{q}\right)\frac{d{U}^{{\prime} }}{d{T}^{{\prime} }}$$
(9)

where \(\frac{d{{T}_{a}}^{{\prime} }}{d{T}^{{\prime} }}\), \(\frac{d{q}^{{\prime} }}{d{T}^{{\prime} }}\) and \(\frac{d{U}^{{\prime} }}{d{T}^{{\prime} }}\) are computed based on the same method as \(\frac{d{Q}^{{\prime} }}{d{T}^{{\prime} }}\) with \({Q}^{{\prime} }\) in Eq. (3) replaced by \({T}_{a}{\prime}\), \(q{\prime}\) and \({U}^{{\prime} }\), respectively. The terms in the first line of the right-hand side of Eq. (9) denote the sensible heat flux feedback (\({\alpha }_{S}\)), with the first to third terms corresponding sequentially to the components related to the background air-sea state (\({\alpha }_{S}^{B}\)), thermodynamic (\({\alpha }_{S}^{{TA}}\)), and dynamic (\({\alpha }_{S}^{{DA}}\)) adjustments of MABL. Similar are the terms in the second line (denoted sequentially as \({\alpha }_{L}^{B}\), \({\alpha }_{L}^{{TA}}\) and \({\alpha }_{L}^{{DA}}\)), but for the latent heat flux feedback. Note that \({\alpha }_{L}^{B}\) is linearly proportional to \(\frac{d{\bar{q}}_{{sat}}}{d\bar{T}}\) that increases with \(\bar{T}\) due to the nonlinearity in the Clausius–Clapeyron relation22,36. To evaluate the validity of decomposition, we compute \({\alpha }_{T}\) directly as \(-\frac{d{{Q}_{T}}^{{\prime} }}{d{T}^{{\prime} }}\). The difference between this direct computation of \({\alpha }_{T}\) and that computed from Eq. (9) is negligible (Fig. 3).