Introduction

The transition state, which is a bottleneck to chemical reactions, governs the overall dynamical aspects such as reaction rates, product branching ratios, or energy disposal dynamics into fragments. Accordingly, the transition state theory1 based on the transition state concept has been enormously successful in describing chemical reactions on adiabatic potential energy surfaces within the Born-Oppenheimer approximation. Although the transition state concept has been firmly established, direct probing of the transition state has long been in a strong wish-list of chemists. Recent decades have seen many experimental and theoretical successes in this endeavor. In the temporal domain, femtochemistry, pioneered by Zewail and Bernstein, captured snapshots of molecules undergoing structural change during chemical reactions2, revealing not only the real-time dynamics of passage through the transition state but also a vibrationally coherent description of the propagating wavepacket3. The recent time-resolved electron or X-ray diffraction studies, in principle, made possible visualization of the three-dimensional movies of the chemical reactions4,5. Generally speaking, however, experiments using the ultrashort laser pulses in the pump/probe scheme suffer an unavoidable limit in terms of the spatial characterization of the transition states in the nuclear configurational space. In this sense, the frequency-resolved spectroscopic studies have been very fruitful in elucidating the quantum mechanical structures of the more tightly defined transition state. For instance, the negative ion photodetachment spectroscopy by Neumark and colleagues revealed rovibrational states of the transition state which are orthogonal to the reaction coordinate of bimolecular reactions6,7. For the unimolecular reaction of ketene (CH2CO* → 3CH2 + CO), the stepwise increasing reaction rate constants measured by Moore and coworkers revealed the quantized thresholds of the molecule at the transition state as implied from the RRKM theory8. The dynamical study of the transition state in both temporal and spatial domains has thus been found to be quite complementary as the former provides the real-time molecular movies whereas the quantum mechanical nature of the transition state could be learned from the latter.

Despite that the pivotal role of the transition state is now conceptually well established, the dynamical behavior of the reactive flux in the proximity of the transition state has been rarely explored to date. Especially for the excited state reactions, vibronic couplings along the multidimensional nuclear coordinates are crucial in dynamically determining the shape of the adiabatic potential energy surfaces underneath the conical intersection9,10,11,12,13. Specifically, the potential energy derivatives with respect to the particular nuclear displacement coordinates in the vicinity of the transition state determine many important dynamical outputs such as the nonadiabatic transition probability, product bifurcation ratios, and reaction rates. In this aspect, a recent report by Field and coworkers is quite noteworthy as the shape of the potential energy surface near the transition state was first revealed for the HCN–HNC isomerization reaction, providing the otherwise unattainable precise location of the transition state through the spectroscopic characterization of the large amplitude vibrational modes14. It should be emphasized though that the spectroscopic characterization of the transition state has been possible only when the corresponding vibrational mode is parallel to the reaction coordinate14,15,16,17,18.

Herein, we have found that one could track the structural change of the reactive flux up to the hill of the potential energy surface along the N-D chemical bond predissociation reaction coordinate of the S1 methylamine (CH3ND2). The highly excited internal rotor (of CH3 with respect to ND2 around the C-N axis) states of CH3ND2 on the S1 surface show a dramatic departure from the theoretical prediction because of the significant structural change in one of the N-D bond lengths. This indicates that the vibronic coupling strength of the internal rotor to the reaction coordinate increases as the reactive flux reaches the reaction barrier maximum, giving the unprecedented information regarding the dynamical behavior of the predissociating molecule in the proximity of the transition state. The structural evolution of the molecule on the verge of the chemical bond rupture has been revealed for the first time by the spectroscopic characterization of the vibrational mode which is apparently orthogonal to the reaction coordinate.

Results and discussion

Methylamine in its first electronically excited state (S1, n3s) is crossed by the high-lying repulsive nσND* state at the first conical intersection to give the underlying adiabatic potential barrier along the N-D bond predissociation reaction coordinate19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38, Fig. 1. Huge H/D isotope effect in the S1 vibronic state lifetime24,25,26,27 indicates that the N-D bond breakage of CH3ND2 occurs via tunneling under the adiabatic reaction barrier of which its height has been theoretically predicted to be ~1500 cm−1 above the S1 zero-point vibrational level20,28,29,30,31,32,35,36,37. The translational energy distributions of the D + CH3ND fragments from the S1 CH3ND2 are bimodal22,23,27,33,34. The Gaussian-shaped high kinetic energy portion reflects the repulsive nature of the potential energy surface in the exit channel whereas the Boltzmann-type low kinetic energy portion should originate from the vibrationally hot molecules in S022,23,27,33,34. This indicates that once the D atom departs from the predissociation on S1, it could either slide down on the repulsive potential energy surface all the way to the asymptotic limit or go back to the ground state at the second conical intersection prior to the subsequent statistical unimolecular reaction. The largest structural change of CH3ND2 in the S1–S0 optical excitation is the bent (S0) to planar (S1) geometrical change of the amino moiety39 accompanied by the quasi-free internal rotation of CH3 with respect to ND2 around the C-N axis in S1 (V6 ~ 5 cm⁻¹) compared to the rather large barrier to the internal rotation in S0 (V3 ~ 690 cm⁻¹)24,25,40,41.

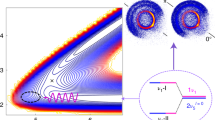
Fig. 1: Potential energy surfaces and S0/S1 quantum states of CH3ND2.
figure 1

a A schematic diagram showing the predissociation dynamics of the S1 CH3ND2. One-dimensional potential energy curves for the S0 and S1 states were calculated by scanning one of the N-D bond lengths of the otherwise frozen molecular geometry at the S1 minimum energy. Photoexcitation to the S1 state using single UV or IR + UV double resonance excitation initiates the N-D bond predissociation via tunneling through the reaction barrier on the adiabatic S1 surface. The inset shows the optimized geometry of CH3ND2 in the S0 (lower) or S1 (upper) state. Two different schemes of IR + UV double resonance excitations were employed; b The IR spectrum of the ground state was recorded by scanning the IR photon energy with the fixed UV wavelength of 243.069 nm. The experiment (black solid line) of the ν11″ band was completely reproduced by the asymmetric rotor simulation (red dashed line) with Trot = 3 K and a linewidth (Γ) of 1.0 cm−1. Rovibrational transitions with relative oscillator strengths are given as sticks. The red arrow depicts the rotational transition at 2984.0 cm−1 corresponding to the S0’ ( J’,Ka’) ← S0” ( J”,Ka”) transitions of (1,0) ← (1,1) and (2,1) ← (3,0). c The DR3PI spectrum was obtained by scanning the UV wavelength with the fixed IR laser at 2984.0 cm−1. d Progression of internal rotor states of which the rotation quantum numbers (m) were assigned from spectral simulations (see the text). Source data are provided as a Source Data file.

Full size image

Although state-selective predissociation dynamics of the S1 methylamine have been intensively studied for many recent years27,30,32,33,34, the explored S1 phase space has been confined within the S1 – S0 Franck-Condon window to date, preventing the thorough understanding of the predissociation mechanism in terms of the vibronic couplings among various nuclear degrees of freedom. Predissociation rate of the S1 CH3NH2 has been predicted to be extremely fast to give τ ~ 300 fs even at the zero-point level according to the earlier-reported spectroscopic works24,25,26. In this aspect, because of homogenously broadened spectral widths, spectroscopic investigation of the S1 CH3NH2 would not be unambiguous in terms of spectral identification and assignment. Furthermore, coupling of the internal rotor onto the reaction coordinate might not be as strong as that in the CH3ND2 case30, though femtosecond time-resolved studies of the S1 CH3NH2 could still be quite worthwhile as it may provide the coherent wavepacket dynamics of the quasi-free internal rotational motion. In this work, we have employed the IR + UV double resonance excitation scheme to explore the otherwise inaccessible S1 quantum states of CH3ND2. This approach turns out to be extremely useful to reveal the vibronic coupling dynamics in the predissociation reaction in terms of the vibrational energy flow of the particular mode into the reaction coordinate especially in the vicinity of the transition state. Indeed, the most spectacular spectral features could be found via the IR + UV double resonance excitation, enabling to observe the highly excited internal rotor states up to its quantum number (m) of 14 corresponding to the S1 internal energy even above the adiabatic reaction barrier maximum. Actually, the IR spectrum of CH3ND2 in S0 has been obtained by monitoring the D fragment from the IR + UV excitation as a function of the IR excitation laser wavelength (2800–3050 cm−1), Fig. 1. Here, the UV laser wavelength was fixed at 243.069 nm (or 41 141 cm−1) not only to further excite the IR-pumped S0 rovibrational states into S1 but also to detect the D fragment via the (2 + 1) multiphoton ionization. Individual rotational transitions could be clearly resolved for the ν11” mode (asymmetric C-H stretching) at ~2990 cm−1 42. The ν11” band was then analyzed using the asymmetric rotor simulation43 at a rotational temperature of 3 K and a bandwidth of 1.0 cm−1. More than six distinct rovibrational bands have been clearly identified with the pairs of specific rotational quantum numbers of the vibrationally excited [S0’ ( J’,Ka’)] and ground [S0 ( J”,Ka”)] states.

The IR laser wavelength was then fixed at 2984.0, 2989.5, or 2994.9 cm−1 for the S0 rotational excitation of ( J’,Ka’) ← ( J”,Ka”), mainly involving the {(1,0),(2,1)} ← {(1,1),(3,0)}, (1,1) ← (0,0), or (2,2) ← (1,1) transition, respectively. And then, the IR + UV double resonance three-photon ionization (DR3PI) spectra were recorded by monitoring the CH3ND2+ parent ion signal while scanning the UV wavelength in the range of 255 – 245 nm. The first UV photon initiates the electronic excitation from the IR-pumped S0’ rovibrational state ( J’,Ka’) into the specific S1 rovibronic state ( J,K), whereas it was ionized by the second UV photon at the same wavelength. Rovibronic structures of the DR3PI spectra are much simplified compared to those of the typical R2PI spectra obtained by the direct UV excitation. Remarkably, the rovibrational structures of the DR3PI spectra are found to be dramatically altered by choosing different rotational transitions of ν11” (see Suppl. Figure 1). Most interestingly, the extremely highly excited internal rotor states anchored at the S1 zero-point vibrational level have been observed in one particular DR3PI spectrum, and we are going to focus on this spectrum in the following.

In the DR3PI spectrum obtained at 2984.0 cm−1 that involves the ( J’,Ka’) ← ( J”,Ka”) transitions of (1,0) ← (1,1) and (2,1) ← (3,0), the extremely high quantum numbers of methyl internal rotor states are observed even above the adiabatic reaction barrier to the N-D bond dissociation (see Suppl. Figures 2 and 3). Taking into account the selection rules of ΔJ = J – J’ = 0, ±1 and ΔK = K – Ka’ = ±1 for the S1 – S0’ transition, the rotational quantum number of the S1 state ( J, K) could be either (1,1) or (2,1) for UV excitation from the ( J’,Ka’) = (1,0) state. On the other hand, the optical excitation from the S0’ ( J’,Ka’) = (2,1) state would give five different S1 rotational states of ( J,K) = (2,0), (1,0), (3,0), (2,2), or (3,2). Quite obviously, therefore, the doublet-like bands represent the rotational structures involved in the S1 – S0’ transitions from the S0’ ( J’,Ka’) = (1,0) state, whereas those excited from the S0’ ( J’,Ka’) = (2,1) state give rise to the more complex rotational contours consisting of at least five well-separated rotational transitions. Accordingly, the S1 rovibronic levels populated from the S0’ ( J’,Ka’) = (1,0) could be unambiguously distinguished from those excited from the S0’ ( J’,Ka’) = (2,1). The long progression bands of the internal rotor up to m = 11 starting from the S1 zero-point level have been clearly identified in the DR3PI spectrum obtained from the S0’ ( J’,Ka’) = (1,0) state. On the other hand, the even longer progressions of the internal rotor mode up to m = 14 anchored at the S1 zero-point level are observed in the DR3PI spectrum obtained via the S0’ ( J’,Ka’) = (2,1) state (see Suppl. Figure 3). For instance, the closely spaced multiple peaks centered at ~ 1055 cm−1 represent the S1 states of (K,m) = (2,−10), (0, ± 11) or (2,12) whereas those at ~1215 cm−1 are ascribed to the (K,m) states of (2,−11), (0, ± 12) or (2,13).

In order to characterize the extraordinarily long progressions of the internal rotor mode, the spectral simulations have been carried out by solving the overall/internal rotor Hamiltonian (H) as follows.

$$H={H}_{{rot}}+{F(p-P)}^{2}+V\left(\phi \right)$$
(1)

Hrot represents the Hamiltonian for the overall rotation whereas F is the effective rotational constant for the internal rotor of top (CH3) with respect to frame (ND2). V(ϕ) is the sixfold torsional potential given by (V6/2) [1 – cos(6ϕ)] where V6 is the barrier height along the torsional angle (ϕ). The (p – P) term is the relative angular momentum of the top and frame. A 100 × 100 Hamiltonian matrix constructed using a free-rotor basis set, \(|{m}{\rangle }=\frac{1}{\sqrt{2\pi }}\exp (-{im}\phi )\), then gives the non-vanishing matrix elements with the symmetric top approximation for Hrot.

$$\left\langle m\left|H\right|m\right\rangle= \left({A}^{F}+{A}^{T}-D{m}^{2}\right){m}^{2}+{BJ}\left(J+1\right)+\left({A}^{F}-{{\rm{B}}}\right){K}^{2} \\ -2{A}^{F}{mK}+({V}_{6}/2)$$
(2)
$$\left\langle m\left|H\right|m\pm 6\right\rangle=-\left({V}_{6}/4\right)\cdot$$
(3)

Here, AF and AT are rotational constants of frame and top, respectively, whereas B is the overall rotational constant and ( J, K) are the angular momentum quantum numbers of CH3ND2 in the S1 state. D is the centrifugal distortion constant inserted for the deviation from the structural rigidity at the high m quantum numbers. The Hamiltonian matrix is then diagonalized to give eigenvalues and associated eigenstates of S1. Ground state energies and associated rotational oscillator strengths for the S0’ – S0 transition are obtained from the PGOPHER program43. As described above, the rotational selection rules for the S1 – S0’ transition from the specific rotational quantum state of S0’ ν11″ determine the DR3PI spectral patterns. For the S1 – S0′ transitions via the S0′ ( J’,Ka′) = (2,1) state, the eigenvalues calculated from the Hamiltonian using the molecular constants of AF = 4.93 cm−1, AT = 4.93 cm−1, B = 0.67 cm−1, D = 0.0020 cm−1, and V6 = 5.0 cm−1 reproduced the experiment perfectly up to m = 8 corresponding to the S1 internal energy (Eint) of ~620 cm−1 24,25. The experiment, however, starts to deviate from the simulation at m = 9 (Eint ~ 770 cm−1) and the deviation becomes significantly larger as m is further increased (m ≥ 10), Fig. 2. For instance, the energy difference between experiment and theory was ~13 cm−1 for m = 9 whereas it sharply increases to ~41 cm−1 for the m = 10 level. It should be noted that the Hamiltonian is anticipated to be little modified for different m quantum numbers especially for the pure internal rotor states anchored at the S1 zero-point level. Furthermore, the intramolecular vibrational redistribution (IVR) is not expected to be significant in the low S1 internal energy (Eint < 1200 cm−1) where the density of states remains quite low. Under these circumstances, the significant and systematic deviation of the experiment from theory should be strong evidence for the geometrical change of the molecule at the highly excited vibrational state15,16,17,18. The most plausible geometrical change with the increase of m should be then the N-D bond length (RND) elongation as the potential energy curve along RND is anticipated to be extremely anharmonic near the reaction barrier maximum in the proximity of the transition state for the N-D bond predissociation20,28,31,32,35,36,37. Geometrical changes other than the extension of RND are expected to be little as the S1 CH3ND2 is most likely confined in the deep potential well with respect to all other internal degrees of freedom other than the quasi-free torsional angle in the corresponding energy region.

Fig. 2: Spectroscopic characterization of the internalrotor vibrational progression bands.
figure 2

(a) The DR3PI spectrum was recorded at the IR photon energy of 2984.0 cm−1. Red-shaded areas depict the internal rotor levels with the internal rotation quantum number of m = 8, 9, or 10 anchored at the S1 zero-point level excited from the S0’ ( J’,Ka’) = (2,1) intermediate state. The experimental spectrum simulated using (b) the fixed molecular rotational constant (AF = 4.93 cm−1) or (c) the energy-dependent values (AF = 4.93, 4.77 or 4.52 for m = 8, 9, or 10, respectively) is given. (d) The m-dependent energies of internal rotor bands observed in the DR3PI spectrum (black circles), showing the systematic deviation from those from the simulations with AF = 4.93 cm−1 (red stars) for high m levels. Source data are provided as a Source Data file.

Full size image

Based on this approach, a set of molecular constants that reproduce the experiment perfectly up to m = 8 had to be modified in order to reproduce the experiment at the higher internal rotor levels above ~700 cm−1, Fig. 2. Namely, taking the ab initio value of 1.042 Å for the N-D bond length at the S1 minimum energy, the experiment was perfectly reproduced by the internal rotational constant (AF) of 4.93 cm−1 up to m = 8. Now, taking the conjecture that the internal rotor is strongly coupled to the reaction coordinate at high m’s, the moment of inertia for the ND2 moiety has been modified to give AF = 4.77, 4.52, 4.04, or 3.82 cm−1 to reproduce the experiment at m = 9, 10, 11, or 12 associated with the transitions from the S0′ ( J’,Ka’) = (2,1) state, respectively. Here, all the other geometric parameters except the N-D bond length (such as the D-N-D angle of 124.3°) were assumed to remain unaltered for all m levels. Though it is less likely, for instance, the D-N-D angle has been modified to see if it could fit the experiment. The simulation requires the D-N-D angle to be increased to 155.2° or > 180° at m = 11 or 12, respectively, from that of 124.3° at the S1 minimum geometry. This unreasonably large increase of the D-N-D angle with the increase of m quantum number cannot be rationalized, and thus it could be completely excluded. The adjusted moment of inertia (AF) to simulate the experiment then represents the S1 molecular structure where one of the N-D bond lengths is extended to 1.076, 1.133, 1.251, or 1.310 Å at m = 9, 10, 11, or 12, respectively. These experimentally determined N-D bond lengths display remarkable behavior when they are plotted versus the S1 internal energy, Fig. 3b. Namely, the N-D bond length gives a sigmoid-shaped increase with the increase of Eint where the RND increment (ΔRND) is maximized at Eint ~ 1000 cm−1. It should be emphasized yet that the N-D bond lengths extracted from our spectroscopic analyzes should be regarded as their upper limits since those are based on the conjecture that only the N-D bond length is allowed to be modified at high m quantum numbers. Nevertheless, the sharp increase of the N-D bond length (ΔRND ~ 0.25 Å) observed in the narrow Eint range of 800–1200 cm−1 should reflect the extremely anharmonic nature of the potential energy curve with respect to the N-D bond elongation coordinate. According to the previously reported ab initio calculations and those by our own group, the transition state for the N-D predissociation of the S1 CH3ND2 is located at RND ~ 1.32 Å with the adiabatic barrier height of ~1500 cm−1 with respect to the S1 zero-point energy level20,28,31,32,35,36,37. This theoretical prediction is surprisingly consistent (even quantitatively) with our experimental determination (e. g. the N-D bond length of 1.310 Å (m = 12) observed at Eint ~ 1215 cm−1), corroborating our conjecture used in the spectroscopic characterization of the internal rotor modes. It should be noted however that the spectroscopic characterization of the internal rotor states of m ≥ 13 at Eint ≥ 1300 cm−1 is not quite straightforward since the DR3PI spectrum at this energy region is broadened and highly congested (Suppl. Figure 3). Nonetheless, the careful assignment on the pure internal rotor states (see Suppl. Note 1) suggests that the N-D bond length might be limited to RND ~ 1.35 Å even above the reaction barrier, Fig. 3b. This upper limit of RND is very close to the theoretical value predicted for the transition state (RND ~ 1.32 Å), implying that the structural change of RND may be limited to the N-D bond length of the molecule at the transition state. This is conceptually consistent with the idea that the vibrational predissociation (Herzberg type-II) on the adiabatic potential energy surface requires that the otherwise orthogonal modes are coupled to the reaction coordinates before the transition state, whereas the N-D stretching becomes pure translational departure motion after the transition state.

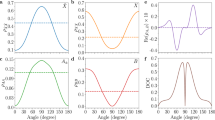
Fig. 3: Dynamical changes of molecularstructure and reactionrate near the reaction barrier maximum.
figure 3

a Energy gap between adjacent internal rotor states, ΔE = E(m) – E(m – 1), plotted versus the internal energy of [E(m) + E(m – 1)]/2. b The energy-dependent variation of the N-D bond length extracted from the simulation to the experiment with the modified internal rotor constants (symbols) and the sigmoidal curve fit (dotted line) for the visual aid. c State-specific S1 decay rates obtained by monitoring parent ion signals using the picosecond time-resolved pump-probe spectroscopy. Error bars are at the 95% confidence level as derived from the non-linear least square fits to the transients. In all plots, the data points are extracted from the S1 ( J,K,m) ← S0’( J’,Ka’) transition of (1,0,-m) ← (2,1) (black circles) or (1,1,-m) ← (1,0) (navy triangles). In plot (c), the rate constants taken from the transitions not belonging to the internal rotor states anchored at the zero-point level are depicted in purple diamonds. The blue-shaded area indicates the reaction barrier maximum for visual comparison across the panels. Source data are provided as a Source Data file.

Full size image

Importantly, it should be noted that the exactly same spectral characterization method could also be applied to the internal rotor states originated from the S0′ ( J’,Ka’) = (1,0) state, Fig. 3b. The N-D bond length has been estimated to be 1.105, 1.192, or 1.299 Å for m = 9, 10, or 11, respectively, from the DR3PI spectrum obtained via the S0′ ( J’,Ka’) = (1,0) state. These structural changes, when they are plotted versus Eint, do perfectly match with those extracted from the DR3PI spectrum taken via the S0′ ( J’,Ka’) = (2,1) state, confirming that the structural changes observed for high m’s are robust and are solely due to the internal rotor excitations near the transition state.

The structural change of CH3ND2 near the transition state is corroborated by the observation of a dip in the plot of the energy gap (ΔE) between adjacent m’s versus Eint, Fig. 3a. More explicitly, the energy gap of ΔE = E(m) – E(m - 1), when plotted versus the x-ordinate of [E(m) + E(m – 1)]/2, shows a kind of Dixon-type dip at Eint ~ 1000 cm−1, which coincides with the energetic position of the largest RND increment. The Dixon dip represents the large anharmonicity of the potential energy curve in the proximity of the transition state where the energy gap between adjacent levels of the particular mode becomes minimized44. For the experimental observation of the Dixon dip, however, the vibrational mode excitation must be parallel to the reaction coordinate and thus it has been observed mostly for the systems undergoing isomerization or pyramidalization reaction14,15,16,17,18, as nicely demonstrated by the Field group where they could give the precise topographical shape of the potential energy surface near the transition state for the HCN – HNC isomerization reaction14. In this aspect, our observation of a Dixon-type dip in the internal rotor levels is unique as it is observed in the highly excited states of the vibrational mode which appears orthogonal to the reaction coordinate. The observation of a dip near the reaction barrier maximum, therefore, reflects the dynamical change in the extent of the projection of the internal rotational motion onto the reaction coordinate as the reactive flux approaches the transition state. This spectroscopic behavior reflects the extremely anharmonic shape of the adiabatic potential energy surface near the transition state resulting from the surface crossing of the bound (n3s) and unbound (nσND*) states whereas it implies at the same time that the nonadiabaticity of the potential energy surfaces may constrain the further extension of the N-D bond length beyond the transition state, thus giving a Dixon-type dip.

In order to obtain the complementary and essential dynamical information, the N-D bond dissociation rate has been directly measured for the first time by the pump-probe method using the narrow-band picosecond laser pulses (Δt ~ 1.7 ps and ΔE ~ 20 cm−1), Fig. 3c. As the major dissipation channel of the S1 CH3ND2 should be the N-D bond cleavage, the parent transient recorded by monitoring the parent ion signal as a function of the delay time between pump (S1–S0 or S1–S0′ excitation) and probe (ionization from S1) wholly represents the N-D bond predissociation rate. At the zero-point level, the S1 lifetime (τ) of CH3ND2 is measured to be ~ 16.4 ± 0.4 ps and this is attributed to the N-D tunneling dissociation reaction. And then, it shows the gradual decrease with the increase of m, giving decrease of the lifetime with τ ~ 16.4, 16.1, 15.6, 14.9, or 14.1 ps at m = (0 and 1), 2, 3, 4, or 5, respectively. The fact that the N-D bond tunneling rate increases with m suggests that the excitation of the internal rotor may help the molecule to escape from the potential well with respect to the N-D extension coordinate. It is in agreement with the previous findings obtained from the slow-electron velocity map imaging (SEVI) experiment30 that the D atom tunneling is accompanied by the vibrational excitation corresponding to the internal rotation of CH3 with respect to ND2. On the other hand, the fact that the increase of the N-D tunneling rate with m is quite small indicates that the coupling of the internal rotor to the reaction coordinate is not significant in the low internal energy region 0 – 300 cm−1. This once again echoes of the spectroscopic result (Figs. 2 and 3b) that the structure of the molecule remains intact in the low m’s (m ≤ 8). Multidimensionality of the tunneling potential energy surfaces has to be invoked for the explanation of the experiment, although the subtle structural change at different m’s (not necessarily with respect to the N-D bond length alone) might also be responsible for the m-dependent behavior of the rate constant at low m’s. Unfortunately, for high m’s (m ≥ 6), since the spectral resolution of the picosecond laser pulse could not resolve the individual internal rotor states, the state-specific tunneling rates could not be rigorously measured. Nonetheless, it has been clearly found that the N-D predissociation rate increases suddenly at Eint ~ 1000 cm−1, strongly indicating that the dissociation reaction is being accelerated as the internal energy reaches the reaction barrier maximum. The energetic location of the sharp increase of the rate constant coincides with that of the N-D bond length (Fig. 3b), indicating that the strong coupling of the internal rotor to the reaction coordinate is perfectly correlated with the increase of the rate constant. This also conforms with the previous finding29,34 that the photofragment excitation signal is strongly enhanced compared to the R2PI signal starting at Eint ~ 1000 cm−1 as well as it rationalizes the significant linewidth broadening observed for high m levels (Suppl. Fig. 9). The reaction rate exhibits a sigmoid-like behavior as the S1 internal energy increases, and this is remarkably in good agreement with the energy-dependent behavior of the N-D bond length deduced from the spectroscopic characterization, giving the precise location of the transition state in terms of the N-D bond length and the barrier height.

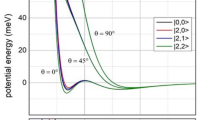
The transition state on the S1 adiabatic potential energy surface has been theoretically predicted to adopt the ciscoid geometry where one of the C-H bonds of CH3 moiety is in the plane of ND2 moiety20,31. The internal rotor barrier at the transition state has been calculated to be ~350 cm−1 at the CASPT2 level, and this is in stark contrast to the quasi-free sixfold potential energy surface with respect to the internal rotation about the C-N axis at the S1 minimum geometry. This suggests that the minimum energy path in the tunneling reaction may be the combination of the N-D bond length extension and internal rotation as the reactive flux should explore the phase space where the N-D bond length is elongated whereas CH3 is rotated with respect to ND2 to adopt the ciscoid geometry at the same time30, also implying that those two structural changes may be combined into the reaction coordinate. This dynamical picture on the two-dimensional potential energy surfaces in the proximity of the transition state conforms with the above argument that the internal rotation is strongly coupled to the N-D bond length extension coordinate, Fig. 4. Actually, this is quite consistent with the present experimental finding that the N-D bond length of the reactive flux is extended with the increase of the internal rotational quantum number, resulting in the sharp increase of the tunneling rate constant near the transition state.

Fig. 4: The structural change of the predissociating CH3ND2 near the transition state.
figure 4

The molecular structures (in terms of the N-D bond length extension) in the vicinity of the transition state result from the strong vibronic coupling of the internal rotor mode into the reaction coordinate. The two-dimensional adiabatic potential energy surface of the S1 CH3ND2 were obtained by the CASPT2 calculations. Source data are provided as a Source Data file.

Full size image

Herein, the structural change of the predissociating molecule in the proximity of the transition state has been revealed by the spectroscopic characterization of the long progression bands of the single vibrational mode which appears orthogonal to the reaction coordinate. We could directly access the highly activated states of S1 CH3ND2 only in terms of the internal rotation of CH3 with respect to ND2 up to its quantum number of 14 by employing the IR + UV double resonance excitation scheme. The internal/overall rotational Hamiltonian is solved to perfectly reproduce the experiment at low m’s whereas it is found that the experiment significantly deviates from the simulation at high m’s, suggesting that the molecule undergoes the structural change toward the geometry at the transition state as the vibrational energy approaches the reaction barrier maximum. The structural change is most probably attributed to the increase of the N-D bond length, and it should be a consequence of the strong coupling of the internal rotor to the reaction coordinate. This is corroborated by the mode-selective rate constants measured in real-time for the N-D predissociation. The sigmoidal behavior of the structural change with respect to the N-D bond length has been found to be perfectly correlated with the energy-dependent predissociation rate constant. This also manifests as a typical Dixon-type dip reflecting the extremely anharmonic nature of the potential energy surface near the transition state.

How does the vibrational energy flow into the reaction coordinate? This has been one of the outstanding dynamical questions in the vibrational predissociation (Herzberg type-II) reaction for a long time. In this regard, this work provides an excellent example where an otherwise orthogonal vibrational mode is coupled to the reaction coordinate to drive the geometrical change of the molecule toward the transition state near the reaction barrier maximum. The geometrical change of the reactive flux has been corroborated by its excellent correlation with the sharply increasing reaction rate with the increase in the S1 internal energy.

In the semiclassical picture where the nuclear motion along the reaction coordinate is classically treated whereas the other orthogonal vibrational modes are taken into account quantum mechanically, it seems that the reactive flux with the high internal rotation excitation, especially when its internal energy is near to the reaction barrier maximum, undergoes a structural change along the otherwise orthogonal N-D bond elongation coordinate to facilitate the tunneling predissociation. In this perspective, it may be stated that the vibrational energy of the internal rotor is partially transferred into the reaction coordinate to stretch the N-D bond length of the molecule on the verge of the chemical bond breakage. Dynamical details regarding the vibronic couplings of orthogonal vibrational modes into the reaction coordinate have rarely been investigated to date, despite that they should provide the essential key for the disentanglement of the otherwise complicated excited state dynamics. In this regard, the current work provides a platform to reveal the dynamical nature of the molecular predissociation in quantum mechanical details.

Methods

Experimental details

The gas mixture of the 3% CH3ND2 in Ne was expanded into vacuum through a 0.5 mm diameter nozzle orifice of the pulsed valve (General valve series 9) operating at a repetition rate of 10 Hz with a backing pressure of ~2 atmosphere. In order to utilize the monomeric molecular beam, the hot front edge of the supersonic jet was collimated by a conical skimmer (Ø = 1.0 mm) before being crossed by counter-propagating nanosecond IR and UV laser pulses in the ion extraction region. The narrow-band IR laser pulse (Δt ~ 10 ns, ΔE ~ 0.5 cm−1, ν = 2800 – 3050 cm−1) was generated from a tunable optical parametric oscillator/amplifier (Laser Vision) pumped by the fundamental output of an injection-seeded Nd:YAG laser (Surelite EX, Continuum). The UV pulse (Δt ~ 10 ns, ΔE ~ 0.3 cm−1, λ = 240 – 255 nm) was obtained by frequency doubling of the output of dye laser (Cobra-Stretch, Sirah) which is pumped by the second harmonic output of another Nd:YAG laser (Surelite II-10, Continuum). The time delay between the IR and UV pulses were maintained to be ~ 20 ns. The nascent ions of the D atom fragment or the parent ions were repelled and extracted in the velocity map ion imaging optics45 before they were drifted through the 25 cm-long field-free region and detected by the position-sensitive microchannel plates coupled to a phosphor screen. The resulting luminescence signal from the phosphor was monitored by a photomultiplier tube and digitized using an oscilloscope before it was transferred into the computer using a LabVIEW-based interface source code. The CH3ND2 transients were obtained by the picosecond (Δt ~ 1.7 ps, ΔE ~ 20 cm−1) time-resolved pump-probe spectroscopy. The 791 nm picosecond laser pulse was generated from a 1 kHz picosecond Ti:Sapphire regenerative amplifier system (Legend Elite-P, Coherent) seeded by a 80 MHz femtosecond oscillator (Vitara-T, Coherent). The picosecond pump (λ = 230 – 255 nm) and probe (λ = 260 nm) laser pulses were obtained by the non-linear frequency mixing through two independent optical parametric amplifier (TOPAS-800, Light Conversion) units pumped by the 5:5 split fundamental output. The pump and probe pulse were collinearly aligned and focused loosely onto the molecular beam in the vacuum chamber through a 1 mm thick CaF2 window. The angle between the polarizations of pump and probe pulses was kept at 54.7° to avoid the rotational effect on the transient. The time delay between pump and probe laser pulses was controlled by a 300 mm-long motorized linear translational stage where a hollow retroreflector unit was mounted. The transients were analyzed by nonlinear least-square curve fits to the Gaussian-convoluted molecular response function to give the decay time constants.

Computational details

The equilibrium geometries of CH3ND2 in the electronically ground and excited states were optimized using the multi-state second-order perturbation (MS-CASPT2) theory46 based on the state-averaged complete active space self-consistent field (CASSCF) reference wavefunction47,48 using a 6-311 + + G(d,p) basis set. Molecular constants, vibrational frequencies, and potential energy surfaces were obtained from the calculations of the S1 equilibrium geometry. The Cartesian atomic coordinates for the S1 equilibrium geometry of CH3ND2 are provided in Supplementary Data 1. The active space was comprised of six electrons and seven orbitals: σCN, σCN*, σND, σND*, 2pN, 3sN, and 3pN. All calculations were performed using the MOLPRO software package49.