Abstract
Waterfalls are anomalies in the angle-resolved photoemission spectrum where the energy-momentum dispersion is almost vertical, and the spectrum strongly smeared out. These anomalies are observed at relatively high energies, among others, in superconducting cuprates and nickelates. The prevalent understanding is that they originate from the coupling to some boson, with spin fluctuations and phonons being the usual suspects. Here, we show that waterfalls occur naturally in the process where a Hubbard band develops and splits off from the quasiparticle band. Our results for the Hubbard model with ab initio determined parameters well agree with waterfalls in cuprates and nickelates, providing a natural explanation for these spectral anomalies observed in correlated materials.
Similar content being viewed by others
Introduction
Angle-resolved photoemission spectroscopy (ARPES) experiments show, quite universally in various cuprates1,2,3,4,5,6,7,8,9, a high energy anomaly in the form of a waterfall-like structure. The onset of these waterfalls is between 100 and 200 meV, at considerably higher energy than the distinctive low-energy kinks10,11,12, and they end at even much higher binding energies around ~1 eV3. Also, their structure is qualitatively very different: an almost vertical and smeared-out waterfall and not a kink from one linear dispersion to another that is observed at lower binding energies. Akin waterfalls have been reported most recently in nickelate superconductors13,14, there starting at around 100 meV. This finding puts the research focus once again on this peculiar spectral anomaly. With the close analogy between cuprates and nickelates15,16 the observation of waterfalls in nickelates gives fresh hope to eventually understand the physical origin of the waterfalls.
Quite similar as for superconductivity, various theories have been suggested for waterfalls in cuprates, including: the coupling to hidden fermions17, the proximity to quantum critical points18, and multi-orbital physics19,20. The arguably most widespread theoretical understanding is the coupling to a bosonic mode, such as phonons21 or spin fluctuations (including spin polarons)22,23,24,25,26. Here, in contrast to the low energy kinks, the electron-phonon coupling appear a less viable origin for waterfalls, simply because the phonon energy is presumably too low. Also the spin coupling J in cuprates is below 200 meV, which however might concur with the onset of the waterfall. But, its ending at 1 eV is barely conceivable from a spin fluctuation mechanism, as it is almost an order of magnitude larger than J. Even the possibility that waterfalls are matrix element effects that are not present in the actual spectral function has been conjectured27.
The simplest model for both, superconducting cuprates and nickelates, is the one-band Hubbard model for the Cu(Ni) 3\({d}_{{{\rm{x}}}^{2}-{{\rm{y}}}^{2}}\) band. In the case of cuprates, the more fundamental model might be the Emery model which also includes the in-plane oxygen orbitals. However, with some caveats such as doping-depending hopping parameters, a description by the simpler Hubbard model is qualitatively similar28,29. In the case of nickelates, these oxygen orbitals are lower in energy, but instead rare earth 5d orbitals become relevant and cross the Fermi level30,31,32,33,34. Still, the simplest description is that of a one-band Hubbard model plus largely detached 5d pockets35,36. This simple description is confirmed by ARPES that shows no additional Fermi surfaces and only 5d A pockets for SrxLa(Ca)1−xNiO213,14.
In this paper, we show that waterfalls naturally emerge when a Hubbard band splits off from the central quasiparticle band. This splitting-off is sufficient for, and even necessitates a waterfall-like structure. Using dynamical mean-field theory (DMFT)37 we can exclude that spin fluctuations are at work, as the feedback of these on the spectrum would require extensions of DMFT38. For the doped model, the waterfall prevails in a large range of interactions, which explains its universal occurrence in cuprates and nickelates. A one-on-one comparison of experimental spectra to those of the Hubbard model with ab initio determined parameters for cuprates and nickelates also shows good agreement. Previous papers pointing toward a similar mechanism9,23,39,40,41,42,43,44,45 have, to the best of our knowledge, been quite general, without the more detailed analysis or understanding which the present paper provides. Among others, Macridin et al.23 noted a positive slope of the DMFT self-energy at intermediate frequencies, but eventually concluded that spin fluctuations lead to waterfalls; Moritz et al.9,41 emphasized that waterfalls simply connect Hubbard and quasiparticle bands; and Sakai et al.40 pointed out the importance of the quasiparticle renormalization and vicinity to a Mott transition, advocating the momentum dependence of the self-energy. All these publications use similar numerical quantum Monte Carlo simulations for the Hubbard model either directly for a finite lattice or for lattice extensions of DMFT. In such calculations, it is difficult to track down whether spin fluctuations23 or other mechanisms9,40,41 are in charge.
Results
Waterfalls in the Hubbard model
Neglecting matrix elements effects, the ARPES spectrum at momentum k and frequency ω is given by the imaginary part of Green’s function, i.e., the spectral function
Here, δ is an infinitesimally small broadening and εk the non-interacting energy-momentum dispersion. For convenience, we set the chemical potential μ ≡ 0. The non-interacting εk is modified by electronic correlations through the real part of the self-energy ReΣ(ω) while its imaginary part describes a Lorentzian broadening of the poles (excitations) of Eq. (1) at
Please note that we have here omitted the momentum dependence of the self-energy which holds for the DMFT approximation, while non-local correlations can lead to a k-dependent self-energy. This k-dependence can, e.g., arise from spin fluctuations and lead to a pseudogap. In Supplementary Figs. 1 and 2, we compare DMFT to an extension of DMFT, the dynamical vertex approximation (DΓA46) that includes such non-local correlations. We show that although non-local correlations can further corroborate the presence of waterfall-like structures, their underlying origin remains tied to local correlations.
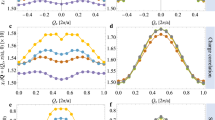
Figure 1 shows our DMFT results for the Hubbard model on the two-dimensional square lattice at half-filling with only the nearest neighbor hopping t. We go from the weakly correlated regime (left) all the way to the Mott insulator (right). The spectrum then evolves from the weakly broadened and renormalized local density of states (LDOS) resembling the non-interacting system in panel (a) to the Mott insulator with two Hubbard bands at ± U/2 in panel (d). In-between, in panel (c), we have the three-peak structure with both Hubbard bands and a central, strongly-renormalized quasiparticle peak in-between; the hallmark of a strongly correlated electron system that DMFT so successfully describes37. Panel (b) is similar to panel (c), with the difference being that the Hubbard bands are not yet so clearly separated. This is the situation where waterfalls emerge in the k-resolved spectrum shown in Fig. 1(j).
Top (a–d): DMFT LDOS for the two-dimensional Hubbard model with nearest neighbor hopping t = 0.3894 eV at half-filling and—from left to right–increasing U. The shaded areas denote the filled states. Temperature is room temperature T = t/15 except for the last column (U = 15t) where T = t. Energies are in units of eV. Middle (e–h): Graphical solution for the poles of the Green’s function in Eq. (2) as the crossing point (colored circles) between εk + ReΣ(ω) (solid lines in three colors for the three k points indicated by vertical lines in the bottom panel) and ω (black dashed line); the colored dashed lines denote εk for the same three momenta. Note that in the insulating case [panel (h)] the dashed lines are shifted by U/2 and the results scaled by a factor of 1/11. Also shown is the imaginary part of the self-energy (light gray; right y-axis). Bottom (i–l): k-resolved spectral function A(k, ω) along the nodal direction Γ = (0, 0) to M = (π, π), showing a waterfall for U = 5t in panel (j). Also plotted are energy distribution curve maxima (EDC MAX, gray circles) and momentum distribution curve maxima (MDC MAX, gray squares) defined as the maxima of A(k, ω) as a function of ω and k, respectively.
Waterfalls from \(\partial {\rm{Re}}{{\Sigma }}(\omega )/\partial \omega=1\)
To understand the emergence of this waterfall feature, we solve in Fig. 1(e–h) the pole equation (2) graphically. That is, we plot the right-hand side of Eq. (2), εk + ReΣ(ω), for three different momenta (colored solid lines), with each momentum indicated by a vertical line of the same color in panels (i-l). The left-hand side of Eq. (2), ω, is plotted as a black dashed line. Where they cross, indicated by circles in panels (i-l), we have a pole in the Green’s function and a large spectral contribution.
For U = 2t (leftmost column), the excitations are essentially the same as for the non-interacting system ω ≈ εk, with the self-energy only leading to a minor quasiparticle renormalization and broadening. In the Mott insulator at large U and zero temperature, on the other hand, Σ(ω) = U2/(4ω). Finite T and hopping t regularize this 1/ω pole seen developing in Fig. 1(h), but then turning into a steep positive slope of ReΣ(ω) around ω = 0. Instead of a delta-function, ImΣ(ω) becomes a Lorentzian (light gray curve; note the rescaling). Thus, while there is an additional pole-like solution around ω = 0, it is completely smeared out.
Now for U = 8t in Fig. 1(g) we have for large ω the same pole-like behavior as in the Mott insulator, though of course with a smaller U2 prefactor. On the other hand, at small frequencies ω we have the additional quasiparticle peak which corresponds to a negative slope ∂ReΣ(ω)/∂ω∣ω=0 < 0 that directly translates to the quasiparticle renormalization or mass enhancement m*/m = 1 − ∂ReΣ(ω)/∂ω∣ω=0 > 1. Altogether, εk + ReΣ(ω) must hence have the form seen in Fig. 1(g): we have one solution of Eq. (2) at small ω in the range of the negative, roughly linear ReΣ(ω), which corresponds to the quasiparticle excitations. We have a second solution at large ω, where we have the 1/ω self-energy as in the Mott insulator, which corresponds to the Hubbard bands. For a chosen k, there is a third crossing in-between, where the self-energy crosses from the Mott like 1/ω to the quasiparticle like—ω behavior. Here, the self-energy has a positive slope. This pole is however not visible in A(k, ω) [Fig. 1(k)], simply because the smearingImΣ(ω) is very large. It would not be possible to see it in ARPES.
However, numerically, one can trace it as the maximum in the momentum distribution curve (MDC), i.e, maxkA(k, ω) along Γ to M, shown as squares in Fig. 1k. This MDC shows an S-like shape since the positive slope of ReΣ(ω) in this intermediate ω range is larger than one (dashed black line). Consequently, for εk at the bottom of the band (orange and blue lines) this third pole in panel (g) is close to the quasiparticle pole, while for εk closer to the Fermi level μ ≡ 0 (green line) it is close to the pole corresponding to the Hubbard band.
For the smaller U of Fig. 1(e), on the other hand, Σ is small and thus also the positive slope in the intermediate ω range must be smaller than one (dashed black line). Together with the continuous evolution of the self-energy from (e) to (j), this necessitates that for some Coulomb interaction in-between, the slope close to the inflection point in-between Hubbard and quasiparticle band equals one: \(\partial {\rm{Re}}{{\Sigma }}(\omega )/\partial \omega=1\). That is the case for U ≈ 5t shown in Fig. 1(k).
Now there is only one pole for each momentum. For the momentum closest to the Fermi level μ (green line), it is in the quasiparticle band where ReΣ(ω) ~ − ω at small ω. When we reduce εk, i.e., shift the εk + ReΣ(ω) curve down, there is one momentum (blue curve) where the crossing is not in the quasiparticle band nor in the Hubbard band but in the crossover region between the two, with the positive slope of ReΣ(ω). As this slope is one, the blue and black dashed lines are close to each other in a large energy region. That is, we are close to a pole for many different energies ω. Given the finite imaginary part of the self-energy, we are thus within reach of an actual pole. Consequently, we get a waterfall in Fig. 1(j) with spectral weight in a large energy range for this blue momentum. Finally, for εk’s at the bottom of the band (orange line), the crossing point is in the lower Hubbard band. Altogether this leads to a waterfall as a crossover from the quasiparticle to the Hubbard band.
Doped Hubbard model
Next, we turn to the doped Hubbard model in Fig. 2. The main difference is that now for the U → ∞ limit, we do not get a Mott insulator, but keep a strongly correlated metal. As a consequence the U-range where we have waterfall-like structures is much wider, which explains that they are quite universally observed in cuprates and nickelates. Strictly speaking, an ideal vertical waterfall again corresponds mathematically to a slope one close to the inflection point of ReΣ(ω). This is the case for U ≈ 8t in Fig. 2c. However, with the much slower evolution with U at finite doping, we have a large U range with waterfall-like structures, first at small U in the form of moderate slopes as in panel (b), and then for large U in form of an S-shape-like structure as in panel (d) that are akin to waterfalls. The survival of the S-shape structure even at U = 15t strongly suggests that it extends up to U → ∞.
Top (a–d): Momentum-resolved spectral function for the two-dimensional Hubbard model with nearest neighbor hopping t = 0.3894 eV—from left to right—increasing U, room temperature T = t/15, and 20% hole doping, showing waterfall-like structures in a large interaction range. Bottom (e–h): Second momentum derivative of the spectral function, which is usually employed in experiments to better visualize the waterfalls. Besides the MDC maxima (MDC MAX, gray squares), we also plot the minima of the second derivative of the MDCs (SD MDC MIN, gray diamonds).
Figure 2 (e-h) shows the second derivative (SD) of the MDC, i.e., ∂2A(k, ω)/∂k2 along the momentum line Γ to M. This SD MDC is usually used in an experiment to better visualize the waterfalls; and indeed we see in Fig. 2e–h that the waterfall becomes much more pronounced and better visible than in the spectral function itself.
Connection to nickelates and cuprates
Let us finally compare our theory for waterfalls to ARPES experiments for nickelates and cuprates. We here refrain from adjusting any parameters and use the hopping parameters of the Hubbard model that have been determined before ab initio by density functional theory (DFT) for a one-band Hubbard model description of Sr0.2La0.8NiO235, La2−xSrxCuO447, and Bi2Sr2CuO6 (Bi2201)48. Similarly, constrained random phase approximation (cRPA) results are taken for the interaction U34,48. CRPA U values of ref. 47 are rounded up similarly to nickelates as in refs. 34,35 to mimic the frequency dependence of U. The parameters are listed in the captions of Figs. 3 and 4.
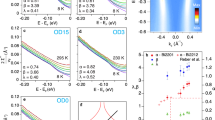
Waterfalls in the one-band DMFT spectrum (a; top) and its second derivative (c; bottom) for Sr0.2La0.8NiO2, compared to experiment13 (exp, golden circles), together with the MDC maxima (MDC MAX, gray squares), and the minima of the second derivative of the MDCs (SD MDC MIN, gray diamonds). In the right column (b; d), we added a broadening Γ = 1 eV to the DMFT self-energy to mimic disorder effects. The ab initio determined parameters of the Hubbard model for nickelates are35: t = 0.3894 eV, \({t}^{{\prime} }=-0.25t,{t}^{{\prime\prime} }=0.12,U=8t\), 20% hole doping, and we take a sufficiently low temperature T = 100/t.
Figure 3 compares the waterfall structure in the one-band Hubbard model for nickelates to the ARPES experiment13 (for waterfalls in nickelates under pressure cf.45). The qualitative agreement is very good. Quantitatively, the quasiparticle renormalization is also well described without free parameters. The onset of the waterfall is at a similar binding energy as in ARPES, though a bit higher, and at a momentum closer to Γ.
This might be due to different factors. One is that nickelate films still have a high degree of disorder, especially stacking faults. We can emulate this disorder by adding a scattering rate Γ to the imaginary part of the self-energy. For Γ = 1 eV, we obtain Fig. 3b, d which is on top of experiment also for the waterfall-like part of spectrum, though with an adjusted Γ. Indeed, we think that this Γ is a bit too large, but certainly disorder is one factor that shifts the onset of the waterfall to lower binding energies. Other possible factors are (i) the ω-dependence of U(ω) in cRPA which we neglect, and (ii) surface effects on the experimental side to which ARPES is sensitive. Also (iii) a larger U would according to Fig. 2 result in an earlier onset of the waterfall. At the same time, it would however also increase the quasiparticle renormalization which is, for the predetermined U, in good agreement with the experiment.
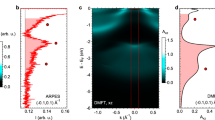
Figure 4 compares the DMFT spectra of the Hubbard model to the energy-momentum dispersions extracted by ARPES for two cuprates. Panels (a-d;g-j) show the comparison for four different dopings x of La2−xSrxCuO4. Again, we have a good qualitative agreement including the change of the waterfall from a kink-like structure at large doping x = 0.3 in panels (d,j) to a more S-like shape at smaller doping x = 0.12 in panels (a,g). The same doping dependence is also observed for Bi2201 from panels (f,l) to (e,k). Note, lower doping effectively means stronger correlations, similar to increasing U in Fig. 2, where we observe the same qualitative change of the waterfall. Altogether this demonstrates that even changes in the form of the waterfall from kink-like to vertical waterfalls to S-like shape can be explained. Quantitatively, we obtain a very good agreement at larger dopings, while at lower dopings there are some quantitative differences. However, please keep in mind that we did not fit any parameters here.
Waterfalls in the DMFT spectrum (top) and its second derivative (bottom) for (a–d;g–j) La2−xSrxCuO4 at four different x and (e, f;k, l) Bi2Sr2CuO6 (Bi2201) for x = 0.16 and x = 0.26 hole doping compared to experiment (golden circles, ref. 2), (green circles, ref. 5). Also shown are the MDC maxima (MDC MAX, gray squares), and the minima of the second derivative of the MDCs (SD MDC MIN, gray diamonds). The ab initio determined parameters of the one-band Hubbard model for La2−xSrxCuO4 are47: t = 0.4437 eV, \({t}^{{\prime} }=-0.0915t,{t}^{{\prime\prime} }=0.0467t,U=7t\). CRPA U values of ref. 47 are rounded up similarly to nickelates as in refs. 34,35 to mimic the frequency dependence of U. Those for Bi2201 are48: t = 0.527 eV, \({t}^{{\prime} }=-0.27t,{t}^{{\prime\prime} }=0.08t,U=8t\) (rounded). Again we set T = 100/t.
Discussion
Umbilical cord metaphor
At small interactions U all excitations or poles of the Green’s function are within the quasiparticle band; for very large U and half-filling all are in the Hubbard bands; and for large, but somewhat smaller U we have separated quasiparticle and Hubbard bands. We have proven that there is a qualitatively distinct fourth “waterfall" parameter regime. Here, the Hubbard band is not yet fully split off from the quasiparticle band, and we have a crossover in the spectrum from the Hubbard to the quasiparticle band in the form of a waterfall. This waterfall must occur when turning on the interaction U and is, in the spirit of Ockham, a simple explanation of the waterfalls observed in cuprates, nickelates, and other transition metal oxides. Even the change from a kink-like to an actual vertical waterfall to an S-like shape with increasing correlations agrees with the experiment.
As Supplementary Movie 1, we provide a movie of the spectrum evolution with increasing U. Figuratively, we can call this evolution the “birth of the Hubbard band", with the quasiparticle band being the “mother band" and the Hubbard band the “child band". The waterfall is then the “umbilical cord" connecting the “mother band" and “child band" before the latter becomes fully disconnected from the former. As a matter of course, such metaphors are never perfect. Here, e.g., we rely on the time axis being identified with increasing U. However, one could also interpret it vice versa, that is, as the quasiparticle band disconnects from the Hubbard band as U decreases.
Methods
In this section, we outline the model and computational methods employed. The two-dimensional Hubbard model for the 3\({d}_{{{\rm{x}}}^{2}-{{\rm{y}}}^{2}}\) band reads
Here, tij denotes the hopping amplitude from site j to site i, which we restrict to nearest neighbor t, next-nearest neighbor \({t}^{{\prime} }\), and next-next-nearest neighbor hopping t″; \({\hat{{c}_{i}}}^{\dagger }\) (\(\hat{{c}_{j}}\)) are fermionic creation (annihilation) operators, and σ marks the spin; \({\hat{n}}_{i\sigma }={\hat{c}}_{i\sigma }^{\dagger }{\hat{c}}_{i\sigma }\) are occupation number operators; U is the Coulomb interaction.
DMFT calculations were done using w2dynamics49 which uses quantum Monte Carlo simulations in the hybridization expansion50. For the analytical continuation, we employ maximum entropy with the chi2kink method as implemented in the ana_cont code51.
Code availability
The w2dynamics code49 is available at github.com/w2dynamics/w2dynamics; the ana_cont code51 is available at github.com/josefkaufmann/ana_cont.
References
Ronning, F. et al. Anomalous high-energy dispersion in angle-resolved photoemission spectra from the insulating cuprate Ca2CuO2Cl2. Phys. Rev. B 71, 094518 (2005).
Meevasana, W. et al. Hierarchy of multiple many-body interaction scales in high-temperature superconductors. Phys. Rev. B 75, 174506 (2007).
Graf, J. et al. Universal high energy anomaly in the angle-resolved photoemission spectra of high temperature superconductors: possible evidence of spinon and holon branches. Phys. Rev. Lett. 98, 067004 (2007).
Inosov, D. S. et al. Momentum and energy dependence of the anomalous high-energy dispersion in the electronic structure of high temperature superconductors. Phys. Rev. Lett. 99, 237002 (2007).
Xie, B. P. et al. High-energy scale revival and giant kink in the dispersion of a cuprate superconductor. Phys. Rev. Lett. 98, 147001 (2007).
Chang, J. et al. When low- and high-energy electronic responses meet in cuprate superconductors. Phys. Rev. B 75, 224508 (2007).
Valla, T. et al. High-energy kink observed in the electron dispersion of high-temperature cuprate superconductors. Phys. Rev. Lett. 98, 167003 (2007).
Zhang, W. et al. High energy dispersion relations for the high temperature Bi2Sr2CaCu2O8 superconductor from laser-based angle-resolved photoemission spectroscopy. Phys. Rev. Lett. 101, 017002 (2008).
Moritz, B. et al. Effect of strong correlations on the high energy anomaly in hole- and electron-doped high-Tc superconductors. N. J. Phys. 11, 093020 (2009).
Lanzara, A. et al. Evidence for ubiquitous strong electron-phonon coupling in high-temperature superconductors. Nature 412, 510 (2001).
Zhou, X. J. et al. Universal nodal Fermi velocity. Nature 423, 398 (2003).
Valla, T., Drozdov, I. K. & Gu, G. D. Disappearance of superconductivity due to vanishing coupling in the overdoped Bi2Sr2CaCu2O8+δ. Nat. Commun. 11, 569 (2020).
Sun, W. et al. Electronic structure of superconducting infinite-layer lanthanum nickelates. Preprint at https://arxiv.org/abs/2403.07344 (2024).
Ding, X. et al. Cuprate-like electronic structures in infinitelayer nickelates with substantial hole dopings. Natl Sci. Rev. 11, nwae194 (2024).
Anisimov, V. I., Poteryaev, A. I., Korotin, M. A., Anokhin, A. O. & Kotliar, G. First-principles calculations of the electronic structure and spectra of strongly correlated systems: dynamical mean-field theory. J. Phys. Condens. Matter 9, 7359 (1997).
Hansmann, P. et al. Turning a nickelate fermi surface into a cupratelike one through heterostructuring. Phys. Rev. Lett. 103, 016401 (2009).
Sakai, S., Civelli, M. & Imada, M. Direct connection between Mott insulators and d-wave high-temperature superconductors revealed by continuous evolution of self-energy poles. Phys. Rev. B 98, 195109 (2018).
Mazza, G., Grilli, M., Di Castro, C. & Caprara, S. Evidence for phonon-like charge and spin fluctuations from an analysis of angle-resolved photoemission spectra of La2−xSrxCuO4 superconductors. Phys. Rev. B 87, 014511 (2013).
Weber, C., Haule, K. & Kotliar, G. Optical weights and waterfalls in doped charge-transfer insulators: a local density approximation and dynamical mean-field theory study of La2−xSrxCuO4. Phys. Rev. B 78, 134519 (2008).
Barišić, O. & Barišić, S. High-energy anomalies in covalent high-Tc cuprates with large Hubbard Ud on copper. Phys. B: Condens. Matter 460, 141 (2015).
Mazur, E. A. Phonon origin of low-energy and high-energy kinks in high-temperature cuprate superconductors. Europhys. Lett. 90, 47005 (2010).
Borisenko, S. V. et al. Kinks, nodal bilayer splitting, and interband scattering in YBa2Cu3O6+x. Phys. Rev. Lett. 96, 117004 (2006).
Macridin, A., Jarrell, M., Maier, T. & Scalapino, D. J. High-energy kink in the single-particle spectra of the two-dimensional Hubbard model. Phys. Rev. Lett. 99, 237001 (2007).
Markiewicz, R. S., Sahrakorpi, S. & Bansil, A. Paramagnon-induced dispersion anomalies in the cuprates. Phys. Rev. B 76, 174514 (2007).
Manousakis, E. String excitations of a hole in a quantum antiferromagnet and photoelectron spectroscopy. Phys. Rev. B 75, 035106 (2007).
Bacq-Labreuil, B. et al. On the cuprates’ universal waterfall feature: evidence of a momentum-driven crossover. Preprint at https://arxiv.org/abs/2312.14381 (2024).
Rienks, E. D. L. et al. High-energy anomaly in the angle-resolved photoemission spectra of Nd2−xCexCuO4: evidence for a matrix element effect. Phys. Rev. Lett. 113, 137001 (2014).
Tseng, Y.-T. et al. Single- and two-particle observables in the emery model: a dynamical mean-field perspective. Preprint at https://arxiv.org/abs/2311.09023 (2024).
Kowalski, N., Dash, S. S., Sémon, P., Sénéchal, D. & Tremblay, A.-M. Oxygen hole content, charge-transfer gap, covalency, and cuprate superconductivity. Proc. Natl Acad. Sci. 118, e2106476118 (2021).
Botana, A. S. & Norman, M. R. Similarities and differences between LaNiO2 and CaCuO2 and implications for superconductivity. Phys. Rev. X 10, 11024 (2020).
Sakakibara, H. et al. Model construction and a possibility of cuprate like pairing in a new d9 nickelate superconductor (Nd, Sr)NiO2. Phys. Rev. Lett. 125, 77003 (2020).
Hirayama, M., Tadano, T., Nomura, Y. & Arita, R. Materials design of dynamically stable d9 layered nickelates. Phys. Rev. B 101, 75107 (2020).
Nomura, Y. et al. Formation of a two-dimensional single component correlated electron system and band engineering in the nickelate superconductor NdNiO2. Phys. Rev. B 100, 205138 (2019).
Si, L. et al. Topotactic hydrogen in nickelate superconductors and akin infinite-layer oxides ABO2. Phys. Rev. Lett. 124, 166402 (2020).
Kitatani, M. et al. Nickelate superconductors—a renaissance of the one-band Hubbard model. npj Quantum Mater. 5, 59 (2020).
Held, K. et al. Phase diagram of nickelate superconductors calculated by dynamical vertex approximation. Front. Phys. 9, 810394 (2022).
Georges, A., Kotliar, G., Krauth, W. & Rozenberg, M. J. Dynamical mean-field theory of strongly correlated fermion systems and the limit of infinite dimensions. Rev. Mod. Phys. 68, 13 (1996).
Rohringer, G. et al. Diagrammatic routes to nonlocal correlations beyond dynamical mean field theory. Rev. Mod. Phys. 90, 25003 (2018).
Matho, K. Kinks and waterfalls in the dispersion of ARPES features. J. Electron Spectrosc. Relat. Phenom. 181, 2 (2010). proceedings of International Workshop on Strong Correlations and Angle-Resolved Photoemission Spectroscopy 2009.
Sakai, S., Motome, Y. & Imada, M. Doped high-Tc cuprate superconductors elucidated in the light of zeros and poles of the electronic Green’s function. Phys. Rev. B 82, 134505 (2010).
Moritz, B., Johnston, S. & Devereaux, T. Insights on the cuprate high energy anomaly observed in ARPES. J. Electron Spectrosc. Relat. Phenom. 181, 31 (2010). proceedings of International Workshop on Strong Correlations and Angle-Resolved Photoemission Spectroscopy 2009.
Tan, F., Wan, Y. & Wang, Q.-H. Theory of high-energy features in single-particle spectra of hole-doped cuprates. Phys. Rev. B 76, 054505 (2007).
Zemljič, M. M., Prelovšek, P. & Tohyama, T. Temperature and doping dependence of the high-energy kink in cuprates. Phys. Rev. Lett. 100, 036402 (2008).
Deng, X. et al. Bad metals turn good: spectroscopic signatures of resilient quasiparticles. Phys. Rev. Lett. 110, 086401 (2013).
Di Cataldo, S., Worm, P., Tomczak, J., Si, L. & Held, K. Unconventional superconductivity without doping in infinite-layer nickelates under pressure. Nat. Comm. 15, 3952 (2024).
Toschi, A., Katanin, A. A. & Held, K. Dynamical vertex approximation; a step beyond dynamical mean-field theory. Phys. Rev. B 75, 45118 (2007).
Ivashko, O. et al. Strain-engineering Mott-insulating La2CuO4. Nat. Comm. 10, 786 (2019).
Morée, J.-B., Hirayama, M., Schmid, M. T., Yamaji, Y. & Imada, M. Ab initio low-energy effective Hamiltonians for the high-temperature superconducting cuprates Bi2Sr2CuO6, Bi2Sr2CaCu2O8, HgBa2CuO4, and CaCuO2. Phys. Rev. B 106, 235150 (2022).
Wallerberger, M. et al. w2dynamics: Local one- and two-particle quantities from dynamical mean field theory. Comp. Phys. Comm. 235, 388 (2019).
Gull, E. et al. Continuous-time Monte Carlo methods for quantum impurity models. Rev. Mod. Phys. 83, 349 (2011).
Kaufmann, J. & Held, K. ana_cont: Python package for analytic continuation. Comp. Phys. Comm. 282, 108519 (2023).
Additional data related to this publication, including input/ output files and raw data for both DMFT and DTA calculations is available at https://doi.org/10.48436/zyqxm-62108.
Acknowledgements
The authors thank Simone Di Cataldo, Andreas Hausoel, Eric Jacob, Oleg Janson, Motoharu Kitatani, Liang Si, Paul Worm, and Yi-feng Yang for helpful discussions. KH and JK acknowledge funding by the Austrian Science Funds (FWF) through Grant DOI 10.55776/P36213. KH further acknowledges funding through FWF Grant DOI 10.55776/I5398, SFB Q-M&S (FWF Grant DOI 10.55776/F86), and Research Unit QUAST by the Deutsche Foschungsgemeinschaft (DFG project ID FOR5249; FWF Grant DOI 10.55776/I5868). The DMFT calculations have been done in part on the Vienna Scientific Cluster (VSC).
Author information
Authors and Affiliations
Contributions
J.K. did the DMFT calculations, analytic continuations, and designed the figures; K.H. devised and supervised the project, and did a major part of the writing. Both authors discussed and refined the project, arrived at the physical understanding presented, and approved the submitted version.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Krsnik, J., Held, K. Local correlations necessitate waterfalls as a connection between quasiparticle band and developing Hubbard bands. Nat Commun 16, 255 (2025). https://doi.org/10.1038/s41467-024-55465-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-024-55465-7