Introduction

Complex networks represent the structure of several natural and artificial complex systems1, that exhibit ubiquitous properties such as heterogeneous connectivity2, efficient information transmission3, mesoscale4 and hierarchical5,6 organization. Moreover, additional information can be used to enrich these models considering multiplexity and interdependence7,8,9,10,11, high-order behavior and mechanisms12,13,14,15,16. The richness of network modeling and analysis opens the door for a wide variety of applications across multiple disciplines, ranging from gene regulation17,18 and protein interaction19 networks in molecular biology, brain networks20,21 in neuroscience, traffic networks22 in urban planning, to social networks23,24 in social sciences.

Furthermore, network science has been used to study the flow of information within networks, from the electrochemical signals traveling between brain areas and pathogens spreading among social systems to the flights in airline networks and the messages being shared on social media. To this aim, often, a dynamical process is exploited that governs the short- to long-range flow between the components25,26,27,28,29,30,31,32,33,34,35,36,37,38,39. Yet, the largeness of many real-world systems poses a challenge, due to computational complexity and components’ redundancies in roles and features, hampering a clear understanding of how complex systems operate. Therefore, an interesting possibility is to search for proper compressions of networks– by means of grouping and coarse-graining nodes with redundant features or roles– that preserve the flow.

The network renormalization method focuses on compressing the size of the network while preserving its core properties. Several pioneering methods have been proposed to coarse-grain the components. Song et al.40 brought the concept of the Box-Covering method into the network renormalization realm41, with subsequent works primarily focused on enhancing its efficiency42,43,44. Generally, these methods treat the network as a spin system45 and study the universality classes46 and fractal properties47. As another example, geometric renormalization on unweighted graph48 and weighted graph49 embeds the network structure into a two-dimensional hyperbolic space, groups the nodes based on their angle similarities, and merge them into a macro network: in that space they unravel the multiscale organization of real-world networks. In the same spirit, the effective geometry induced by network dynamics have been used to uncover the scale and fractal properties50. As an example, spectral coarse graining51 focuses on the dynamics on top of networks and attempts to preserve the large-scale random walk behavior of the network during structural compression. More recently, an approach based on Laplacian renormalization52 was proposed based on diffusion dynamics on top of the network, corresponding to the renormalization of a free field theory in network structures. This method pushed the boundaries of RG to include structural heterogeneity by preserving the slow modes of diffusion. However, none of these renormalization methods is designed to preserve the macroscopic features of information dynamics simultaneously at all propagation scales for all network types.

Similar to the Laplacian renormalization group, we capitalize on network density matrices33 to describe the information dynamics in the system53. From density matrices, we derive the typical macroscopic indicators like network entropy and free energy, which, respectively, quantify how diverse the diffusion pathways are53,54,55 and how fast signals travel in the system55,56. We show that such measures can be derived from the network partition function Zτ, as in equilibrium thermodynamics. On this theoretical basis, we deduce that a coarse-graining that preserves the shape of partition function across the propagation scale τ, preserves the macroscopic indicators of information flow. Therefore, we aim to reach a coarse-graining with minimum deviations from the full partition function profile.

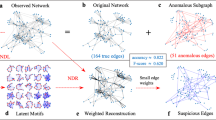
We bypass the challenge of finding an analytically closed solution for general complex networks. Avoiding simplifying assumptions and cases of poor practical interest, we leverage recent advances in machine learning based on graphs to develop the framework of the Network Flow Compression Model(NFC Model), as depicted in Fig. 1. More technically, we use graph neural networks57,58 to process and aggregate nodes’ local features like the number of connections (degree), and reach a high-level representation of them. In the representation space, it identifies groups of nodes that play redundant roles in information flow whose aggregation does not drastically change the flow and coarse-grain them to reach suitable compressions, minimizing the partition function deviation. While most coarse-graning methods define and identify supernodes by grouping nodes with similar local structures, their notion of similarity is typically predefined48,49. In contrast, our approach leverages a machine learning model to automatically learn the vital similarity features that can be used to compress the network while preserving the macroscopic flow properties. For instance, in the BA network, hub nodes are coarsened together, while leaf nodes are coarsened together. In real-world scientist collaboration networks, scientists with the highest number of collaborations are coarsened into one group, even if they don’t collaborate with(are connected to) each other. Experimental results in subsequent sections and show that our approach preserves the information flow even for large compressions, in synthetic and empirical systems. The analysis of the model’s interpretability in subsequent sections indicates that this strategy is reasonable: it preserves the function of local structures in the process of information diffusion while reducing the number of redundant structures.

Fig. 1: A Schematic representation of our framework.
figure 1

The message-passing mechanism of the GNN collects neighbors' information to create a vector representation for each node. The Softmax method normlizes the vector leading to a node grouping. The node features we use here include degree σd, degree’s \({{{{\mathcal{X}}}}}^{2}\)--- i.e., given by \({{{{\mathcal{X}}}}}_{i}^{2}={(E[d]-{\sigma }_{d})}^{2}/E[d]\) where d is the degree of neighboring nodes---, clustering coefficient and core-number. In this case, 3 groups are considered for simplicity, represented in the group matrix S. Using both S and the original adjacency matrix A, we proceed with a compression operation expressed as: \(\hat{{{{\bf{A}}}}}=\frac{M}{N}{{{{\bf{S}}}}}^{T}{{{\bf{A}}}}{{{\bf{S}}}}\). In this operation, \(\hat{{{{\bf{A}}}}}\) stands for the adjacency matrix of the macro network, whereas M and N symbolize the number of nodes within the macro and micro networks, respectively. The deviation of macro network’s normalized partition function from the original network is used as the loss function to supervise the GNN.

Full size image

Our work serves a purpose that is ultimately different from the network renormalization group methods. In fact, these methods aim to uncover the scaling behavior of systems. For instance, renormalization group methods preserve specific topological properties when compressing networks, like the degree distribution of scale-free networks. However, in other cases, for instance, in network with one or multiple characteristic topological scales, these methods are expected to capture the changes in network properties, including the flow, as it gets compressed. In contrast, our approach seeks to find a coarse-graining that preserves the flow properties, regardless of the specific features of a topology. Therefore, it is expected to outperform others in preserving the flow, when compared across distinct network families. We confirm this expectation through a series of numerical experiments demonstrated in Fig. 2.

Fig. 2: Compression for Synthetic Networks.
figure 2

Visual representation of the compression process applied to two representative Stochastic Block Model (SBM) networks (mixing parameters μ of 0.029 and 0.127, respectively) and Barabasi-Albert (BA) networks (numbers of links per node m of 1 and 2). The second row visualizes the structure of the macro network that was compressed to 35 nodes. The third row shows the Mean Absolute Error in the partition function before and after compression at different sizes. We selected 10 different sizes uniformly in the logarithmic space between 5 and 200. The last row shows the Mean Absolute Error of the partition function curve for different methods when compressing the network to 35 nodes.

Full size image

Finally, we train our graph neural networks on a vast number of real-world networks, enabling generalization to the datasets it has not seen before. We show that it leads to rapid and highly effective compressions across networks from various domains.

Results

Macroscopic indicators for information flow

Let G be a network of N nodes and ∣E∣ connections, respectively. The connections are often encoded by the adjacency matrix A, where Aij = 1 if nodes i and j are connected, and Aij = 0 otherwise. For a weighted network, the values Aij can be non-binary. Information exchange between the components happens through the connections.

We focus on diffusion as one of the simplest and most versatile processes to proxy the flow of information59 governed by the graph Laplacian matrix L = D − A, where D is a diagonal matrix, with Dii = ki being the connectivity of node i. Consequently, we write the diffusion equation and its solution:

$${\partial }_{\tau }{\psi }_{\tau }=-{{{\bf{L}}}}{\psi }_{\tau },\\ {\psi }_{\tau }={e}^{-\tau {{{\bf{L}}}}}{\psi }_{0},$$
(1)

where ψτ is a concentration vector, describing the distribution of a quantity over nodes and e−τL gives the time-evolution operator, with \({\left.{e}^{-\tau {{{\bf{L}}}}}\right]}_{ij}\) giving the flow from node j to i after τ time steps.

The network density matrix can be defined as

$${{{{\boldsymbol{\rho }}}}}_{\tau }=\frac{{e}^{-\tau {{{\bf{L}}}}}}{{Z}_{\tau }},$$
(2)

where \({Z}_{\tau }={{{\rm{Tr}}}}\,({e}^{-\tau {{{\bf{L}}}}})\) is the network counterpart of the partition function. In fact, Eq. (2) describes a superposition of an ensemble of operators (the outer product of eigenvectors of the Laplacian matrix) that guide the flow of information in the system53,60, with applications ranging from classification of healthy and disease states39,61 and robustness analysis62,63 to dimensionality reduction of multilayer networks56 and renormalization group52.

More importantly, the network Von Neumann entropy defined by \({{{{\mathcal{S}}}}}_{\tau }=-{{{\rm{Tr}}}}\,({{{{\boldsymbol{\rho }}}}}_{\tau }\log {{{{\boldsymbol{\rho }}}}}_{\tau })\) has been studied as a measure of how diverse the system responds to perturbations53,54, and the network free energy, \({F}_{\tau }=-\log {Z}_{\tau }/\tau\), as a measure of how fast the signal transport between the nodes55,56.

Since the network density matrix is Gibbsian (Eq. (2)) and the network internal free energy can be defined as \({U}_{\tau }={{{\rm{Tr}}}}({{{\bf{L}}}}{{{{\boldsymbol{\rho }}}}}_{\tau })\), we can write the network free and internal energy and Von Neumann entropy in terms of Zτ and its derivative:

$${F}_{\tau }=-\!\log {Z}_{\tau }/\tau$$
(3)
$${U}_{\tau }=-\!{\partial }_{\tau }\log {Z}_{\tau }$$
(4)
$${S}_{\tau }=\tau ({U}_{\tau }-{F}_{\tau }),$$
(5)

exactly like in equilibrium thermodynamics. It is noteworthy that having a compressed network with a compressed Zτ matching the one of the original network mathematically guarantees identical global information dynamics, measured in terms of macroscopic physics indicators such as network entropy and free energy. We consider a compression where the system changes size from N \({N}^{{\prime} }\), leading to a new Laplacian \(({L}^{{\prime} })\) and a new partition function \(({Z}^{{\prime} })\). Here, we aim to reach a compression that follows:

$$Z=\gamma {Z}^{{\prime} },$$
(6)

regardless of τ, with minimum error.

In fact, if the two networks have different sizes, the only valid value for the multiplier is \(\gamma=N/{N}^{{\prime} }\). A simple argument to support this claim is that at τ = 0 it can be shown that Z = N and \({Z}^{{\prime} }={N}^{{\prime} }\), regardless of the network topology. Therefore, the only solution not rejected by the counter example of τ = 0, which gives the maximum value for the partition function, is \(\gamma=N/{N}^{{\prime} }\). If \(\gamma=N/{N}^{{\prime} }\) with N and \({N}^{{\prime} }\) being the sizes of the original and the reduced systems, these transformations can be interpreted as size adjustments.

We show that such a compression simultaneously preserves other important functions, like entropy and free energy, after size adjustment. For instance, the system’s entropy has its maximum \(S=\log N\) at τ = 0, which can be transformed into the compressed entropy with the subtraction of the factor \(\log \gamma\) as size adjustment \(S\to S-\log \gamma\). Similarly, for free energy \(F=-\log Z/\tau\), the size required adjustment reads \(-\log Z/\tau \to -\log Z/\tau+\log \gamma /\tau\).

The partition function transformation we discussed earlier (Z → γZ, and therefore \({Z}^{{\prime} }=Z/\gamma\)), automatically guarantees both transformations:

$${S}^{{\prime} } =-\tau {\partial }_{\tau }\log {Z}^{{\prime} }-\tau {F}^{{\prime} }\\ =-\tau {\partial }_{\tau }\log {Z}^{{\prime} }+\tau \log {Z}^{{\prime} }\\ =-\tau {\partial }_{\tau }[\log Z-\log \gamma ]+\log Z-\log \gamma \\ =S-\log \gamma,$$
(7)
$${F}^{{\prime} }=-\frac{\log {Z}^{{\prime} }}{\tau }=-\frac{\log Z/\gamma }{\tau }=F+\frac{\log \gamma }{\tau }.$$
(8)

Also, since the von Neumann entropy of the coarse-grained system is given by

$${S}^{{\prime} }=\tau {U}^{{\prime} }+\log {Z}^{{\prime} },$$
(9)

the transformation of the internal energy can be obtained as:

$$S+\log \gamma =\tau {U}^{{\prime} }+\log \gamma+\log Z,\\ \tau U+\log Z =\tau {U}^{{\prime} }+\log Z,\\ U ={U}^{{\prime} },$$
(10)

In the following section, we use machine learning to find compressions replicating the original entropy and free energy curves by approximating \({Z}^{{\prime} }=Z/\gamma\), for all network types across all values of τ.

Machine learning model

Graph neural networks are a class of models suited for machine learning tasks on graphs that leverage node features as structural information64,65. Based on the fundamental idea of aggregating and updating node information with learnable functions, graph neural networks have spawned numerous variants such as graph convolutional networks66, graph attention networks67, graph isomorphism networks68, and graph Transformers69. They have been widely applied to problems such as node classification70, structural inference71, generative tasks72, and combinatorial optimization tasks73 on graphs.

Our approach to solving the network compression problem using graph neural networks is illustrated in Fig. 1. Here, we employ graph isomorphism networks to aggregate node features and decide on the grouping of nodes. Nodes within the same group are compressed into a supernode. Also, the sum of their connections becomes a weighted self-loop of the supernode. Of course, the inter-group connections shape the weighted links between different supernodes. To assess how effective a coarse-graining is, we compare the Mean Absolute Error (MAE) of the normalized partition functions, \(\frac{Z}{N}\), where N is the number of nodes in the original network or the compressed one. Therefore, MAE is the loss function that we use to train the graph neural network. Note that, through the optimization, the model continuously adjusts the mapping from node local structural features to node groupings, using gradient descent. This adjustment ensures that the resulting macroscopic network has a partition function resembling the original network.

Here we mention a number of suitable properties of our model. First, since every edge in the original network becomes a part of a weighted edge in the macroscopic network, the connectedness of the network is guaranteed. If the original network is connected, the macroscopic network will also be connected. Second, the number of nodes in the macroscopic network can be flexibly configured as a hyperparameter that can be tune to satisfy different tasks. Lastly, as we show in the next sections, the time complexity of our model is O(N + E), where N and E are the number of nodes and edges in the original network, respectively. This is a considerable edge over other models that often perform at O(N3)— including box-covering, laplacian RG, or O(N2)— for instance, geometric RG. For this reason, we are able to compress very large networks. Please see the supplementary material for a more detailed analysis of time complexity (Supplementary Note 7) and experiment on network compression with 100,000 nodes (Supplementary Fig. 3).

How our method differs from Laplacian Renormalization Group (LRG)

Since both methods use network density matrices, it is necessary to discuss their differences. The LRG was among the first to introduce Kadanoff’s decimation based on diffusion dynamics on networks as the core of the renormalization process. It has successfully pushed the boundaries of RG to include structural heterogeneity, a feature widely observed in complex systems. To do so, LRG focuses on the specific heat at the specific scale of phase transition to define their information cores52,60 and use them to perform renormalization.

It is crucial to note that the difference between LRG and our method is not limited to the machine learning implementation. Instead, the fundamental difference is in the theoretical conceptualization of the RG problem. We base our method on the fact that the partition function contains the full information of the macroscopic descriptors of the flow, including network entropy and free energy— as demonstrated in the previous sections. Therefore, by trying to replicate the full partition function profile at all propagation scales (all values of τ) we replicate the macroscopic features like the diversity of diffusion pathways and the flow speed in reaching distant parts of the network.

It is worth mentioning that LRG can be used to renormalize at any particular scale (τ). However, they discard the fast modes of diffusion processes (corresponding to eigenvalues greater than \(\frac{1}{\tau }\)). Instead, our method preserves the complete distribution of eigenvalues at all scales simultaneously by maintaining the full behavior of the partition function

Finally, in addition to the discussed theoretical arguments, we use various numerical evidence to demonstrate that our domain of applicability is much larger than LRG’s. As mentioned before, LRG is designed for heterogeneous networks like Barabasi-Albert (BA) and scale-free trees. However, the topology of real-world networks is not limited to what the BA model can generate. The two decades of network science have revealed that real-world networks also exhibit important features such as segregation while integration and order while disorder— i.e., modules, motifs, etc. That is why the compression methods must eventually go beyond the current limitations and model-specific assumptions.

In the following sections, we compare the performance of NFC Model and other widely used methods, including LRG, on both synthetic and empirical networks. Please see the supplementary Note 3 for a more detailed comparison with LRG on different datasets regarding the preservation of information flow (Supplementary Fig. 5) and entropy (Supplementary Fig. 7), the retention of eigenvalue distributions (Supplementary Fig. 6), and differences in supernode composition (Supplementary Fig. 8) and macroscopic network structures (Supplementary Fig. 9)— which comparison clearly shows a large difference between our method and LRG, both in the performance and the way they group nodes together.

Synthetic networks compression

Here, we use our model to compress four synthetic networks: two Stochastic Block Model (SBM) with mixing parameters (μ) of 0.029 and 0.127, and two Barabási–Albert (BA) models with parameters m = 1, 2, all with 256 nodes (See Fig. 2).

As expected, for very large compressions, we find an increase in the deviation between partition functions— i.e., cost. However, interestingly, the compression error exhibits an approximately scale-free relationship with network size, meaning that no compression size is special. We visualize the compressed network with 35 nodes in the second row of subfigures in Fig. 2, where the nodes in the compressed network and the corresponding nodes in the original network were assigned the same color.

We show that our approach outperforms others including Box-Covering, Geometric Renormalization, and Laplacian Renormalization. Also, our results indicate that the mesoscale structure of SBM and the presence of hubs in BA play important roles in the topology of the resulting compressed network. The nodes belonging to the same community in the original SBM networks often group together to form a supernode in the macro-network. More surprisingly, in the BA network, nodes with a similar number of connections were typically coarse-grained together.

This finding suggests that regardless of being directly connected or not, nodes with similar local structures need to group together when the goal is recovering the flow of information. Here, the coarse-graining of nodes with similar local structures is learned by the model automatically and was not predetermined a priori.

Empirical networks compression

We analyze two representative empirical networks to test the capability of our method. The networks include the U.S. Airports, taken from Open Flights and Netzschleuder, and the Scientists Co-Authorship Network used in 200674.

In the U.S. Airports Network, nodes and edges represent airports and flight routes between them— i.e., a binary and undirected edge connects two airports if there is at least one flight between them. Similarly, in the co-authorship network, nodes are individual researchers, and an edge exists between two scientists if they have co-authored at least one paper. (For more details on the datasets, see Table 1).

Table 1 Statistics for two real-world networks
Full size table

Firstly, we reduce the US airport network up to 50 and 20 supernodes compression sizes (See Fig. 3). We highlight the 15 airports with the highest connectivity, located in the cities of Atlanta, Denver, Chicago, Dallas-Fort Worth, Minneapolis, Detroit, Las Vegas, Charlotte, Houston, Philadelphia, Los Angeles, Washington, Salt Lake City, and Phoenix. Interestingly, these 15 airports group together to form only a few supernodes, owing to their similar local structures— i.e., degree, in this case— in both compressions. Furthermore, in the 50-node macro-network, cities like Atlanta and Denver are compressed into one supernode, and cities such as Detroit and Las Vegas shape another supernode. Whereas, in the compression with 20 supernodes, cities including Atlanta, Denver, Detroit and Las Vegas join into one single supernode.

Fig. 3: Compression of empirical networks.
figure 3

The U.S. Airport Network and the Co-Authorship network of scientists (2006) alongside the corresponding compression outcomes under different macro node configurations. We further illustrate the macro nodes associated with the top 15 airports and top 5 scientists as determined by node degree, some of the top nodes are marked in the original network. It becomes apparent that these most emblematic nodes primarily cluster within a limited number of macro nodes, supporting the hypothesis that nodes with similar local structures gravitate towards similar groups. As the macro airport network shrinks, these nodes amalgamate into fewer macro nodes, suggesting that the diminishing expressivity of the macro network necessitates the model to overlook the distinctions between these nodes. The three subsequent subgraphs delineate the Mean Absolute Error (MAE) of the normalized partition functions in the compression results derived from our method against other competitive approaches. It is worth noting that, due to the inability of some comparative methods (such as Box-Covering) to precisely control the size of the network after compression, we allow them to compress a network larger than the target size and compare it with our method.

Full size image

The compression of the network scientist system confirms the previous results (See Fig. 3). For instance, the five highest-degree researchers of this dataset, including Barabasi, Jeong, Newman, Oltvai, and Boccaletti, form one supernode, when the size of the macro-network is 10. Note that they are not a tightly connected group in the original network. In fact, Newman, Barabasi, and Boccaletti are not even connected in this network. This further suggests that having similar local structures in the network is a key factor in compression.

Finally, we compare the partition function deviation achieved by different compression methods and show that our approach clearly outperforms others (See Fig. 3), in the case of both empirical systems. For more detailed information on the groupings of all airports, please see Supplementary Table 1.

Overall, confirming the synthetic networks analysis, our approach generates macro networks closely resembling the information flow in the original networks by coarse-graining nodes of similar local structures.

Interpretability of the compression procedure

In experiments with both synthetic and real-world networks, we found that our machine-learning model merges nodes with similar local structures to preserve information flow. Here, we attempt to provide an explanation of how exactly it works.

Firstly, clustering nodes with similar local structures together preserves the function of that local structure within the original network while reducing structural redundancy. This can be intuitively understood through the analysis of several typical topological features.

High clustering coefficient nodes

Nodes with a high clustering coefficient often have neighbors that are interconnected, acting to trap information locally during the diffusion of information in the network. Grouping nodes with a high clustering coefficient together, their numerous interconnections will become a high-weight self-loop on the supernode, similarly playing a role in trapping information locally, as shown in Fig. 4, subplot a.

Fig. 4: Grouping strategies and the structure of the macroscopic network.
figure 4

a Illustration of the compression of nodes with high clustering coefficients. Both the high-clustering nodes and their corresponding macro-nodes tend to trap information locally. b Demonstration of the compression of hub nodes. Both the hub nodes and their corresponding macro-nodes act as bridges for global information diffusion. c Compression of community structures: Nodes within the same community are compressed into a supernode, which, similar to the original community structure, tends to trap information locally. d We show the macroscopic network after compression using different hard(discrete) grouping strategies for a toy network with 8 nodes and 5 types of different local structures, and the changes in the corresponding partition function. e The soft(continuous) grouping strategy learned by our model. In (f) we present the macroscopic network structure given by the grouping strategy from (e). g Comparison of the normalized partition function error before and after compression under different grouping strategies.

Full size image

Hubs

Hub nodes act as bridges for global information diffusion within the network. By clustering hub nodes together, the edges between hub nodes and other nodes transform into connections between supernodes in the compressed network, still ensuring the smooth passage of global information. Suppose we group a hub node and its neighbors into one; then, their interconnections become self-loop of that supernode that trap the information locally, acting as a barrier to global information transmission, as shown in Fig. 4, subplot b.

Strong communities

Networks with distinct community structures experience slow global information diffusion (due to few inter-community edges). Grouping nodes of the same community together transforms the numerous intra-community edges into self-loops on the supernodes, trapping information locally. Meanwhile, the few inter-community edges become low-weight edges between supernodes, similarly serving to slow down the speed of global information diffusion as shown in Fig. 4, subplot c. Through these three typical examples, we find that structural redundancy has been reduced while the corresponding functions are preserved. Therefore, this approach naturally benefits the preservation of information flow when compressing networks.

Then, based on the principle that “nodes with similar local structures are grouped together," the graph neural network still needs to optimize the specific grouping strategy. This is mainly because, on one hand, the number of groups is often far less than the number of types of nodes with different local structures (imagine a network with 3 different types of nodes, whereas we need to compress it into a macro network with 2 nodes). On the other hand, our model produces continuous grouping results, for example, a certain type of node might enter group A with an 80% ratio and group B with a 20% ratio. Each different ratio represents a new grouping strategy, and we need to find the most effective one from infinitely many continuous grouping strategies, which is an optimization problem, hence requiring the aid of a machine learning model. Subplots d − f of Fig. 4 show discrete grouping strategies and the learned continuous grouping strategy for compressing a network with 5 types of nodes into a macroscopic network with 4 supernodes.

From Fig. 4, we can see that different discrete grouping strategies produce different macroscopic network structures (subplot d), our learned continuous grouping strategy (subplot e), the macroscopic network structure (subplot f), and the partition function difference corresponding to different grouping strategies (subplot g). It is evident from the figure that the error in preserving information flow with our learned continuous grouping strategy is lower than that of all discrete grouping strategies. In summary, this is how our model works: based on the fundamental useful idea that “nodes with similar local structures enter the same group," our model uses the gradient descent algorithm to select one of the infinitely many solutions (continuous grouping strategies) that results in a lower error of the partition function.

Compressing networks from different domains

To further explore the applicable fields of our model, we conducted further analysis on various real networks and attempt to understand the differences in compression outcomes across different domains. In our upcoming experiments, we have selected 25 networks from 8 different fields: biological networks, economic networks, brain networks, collaboration networks, email networks, power networks, road networks, and social networks. Their node number ranges from 242 to 5908, and the number of edges ranges from 906 to 41,706. See Supplementary Table 2 for more information of these networks.

We compressed all networks at various scales, with compression ratios ranging from 1% and 2% up to 25% of the original network size. We aimed to explore how the effectiveness of compression varies with the compression ratio across networks from different domains. The results are shown in the left subplot of Fig. 5. First, we observed that in most of the cases, the error of the normalized partition function (measured by Mean Absolute Error) is less than 10−2, indicating that our model performs well across networks from different domains. Moreover, regarding the differences between networks from various domains, we found that the density of the network has a major impact on compression efficiency. As shown in the right subplot of Fig. 5, we plotted the density against the error in the partition function before and after compression for all networks, and observed a positive correlation(correlation coefficient of 0.856): a network with lower density tends to be more easily compressed. It is plausible that this happens because an increase in the number of connections makes the pathways for information transmission more complex, thereby increasing the difficulty of compression.

Fig. 5: Compressing empirical networks from different domains.
figure 5

In the left subplot, we show the pre- and post-compression partition function error (measured by MAE) for 25 networks from 8 different domains at various compression ratios, ranging from 1% to 25%. In the right subplot, we display the relationship between the average compression error and the network’s density when the compression ratio is greater than 0.1 (at this point, the compression error is not quite sensitive to the compression size, which can be considered as the best compression error achievable by the model without being limited by size).

Full size image

One compression model for many real-world networks

In previous sections, a separate GNN was trained to learn a compression scheme tailored to a specific network. Despite the satisfactory compression results, learning a new neural network for each dataset can be computationally costly. Therefore, we generalize the previous model and train it on a large set of empirical networks. We show that this generalization can compress new networks, the ones it hasn’t been trained on, without any significant learning cost.

First, we gather a dataset with 2, 193 real-world networks spanning various domains, from brains and biological to social and more, with the number of nodes ranging from 100 to 2, 495, from Network Repository (NR)75 (for more information about the dataset, training, and testing process, please see Supplementary Note 6). We randomly select the networks with size smaller than 1000 as the training set and keep the remaining networks as the test set. We apply one model to numerous networks, compress them to macro-networks, and calculate the loss in terms of partition function deviation. The results demonstrate highly effective learning that can successfully compress the test set, generating macro-networks that preserve the flow of information.

This pre-trained model directly possesses the capability to compress networks from different domains and sizes, and it reduces the computational complexity by orders of magnitude, outperforming existing methods. More technically, the time complexity of our model is O(N + E), where N is the system’s size and E the number of connections – which overall drops to O(n) for sparse networks – while the time complexity of other compression models often reaches O(N3) (box-covering, laplacian RG) or O(N2)(geometric RG). To better quantify the model’s time complexity, we validated it on a dataset with a much wider range of sizes. The results are shown in Fig. 6.

Fig. 6: Pre-Trained Mode: Running Time vs. Network Size.
figure 6

In this figure, we show the time required for a pre-trained model to run on W-S networks with different numbers of nodes and connections. The X-axis represents the number of nodes, and the Y-axis shows the time needed to compress the network.

Full size image

Discussion

In network compression methods, a method that can accurately preserve the full properties of the network information flow across different structural properties is still missing. Traditional methods rely on sets of rules that identify groups of nodes in a network and coarse-grain them to build compressed representations. Instead, we take a data-driven approach and extract the best coarse-graining rules by machine learning and adjusting model parameters through training. In contrast with most network compression methods that try to maximize the structural similarity between the macro-network and the original network, our model tends to preserve the flow of information in the network and, therefore, is naturally sensitive to both structure and dynamics.

To proxy the flow of information, we couple diffusion dynamics with networks and construct network density matrices— i.e., mathematical generalizations of probability distributions that enable information-theoretic descriptions of interconnected non-equilibrium systems. Density matrices provide macroscopic descriptors of information dynamics, including the diversity of pathways and the tendency of structure to block the flow. Here, we show that similar to equilibrium statistical physics, the network counterpart of the partition function contains all information about other macroscopic descriptors. Therefore, to preserve the flow of information through the compression, we train the model using a loss function that encodes the partition function deviation of the compressed system from the original networks.

We use the model to compress various synthetic networks of different classes and demonstrate its effective performance, even for large compressions. Then, we analyze empirical networks, including the US airports and researchers’ collaborations, confirming the results obtained from the analysis of synthetic networks.

Our work shows that one way to preserve the information flow is to merge the nodes with similar local structures. With this approach, we can reduce redundant structures while preserving the function of these structures in the original network. Note that this result is an emergent feature of our approach and not an imposed one. One significant feature of our method is that it is not constrained to localized group structures: units that are merged together through the compression process are not necessarily neighbors and can even belong to different communities.

We train the neural networks on thousands of empirical networks and show the effectiveness of generalization and excellent performance on new data. This results in a significant reduction in time complexity. While the time complexity of other compression models often reaches O(N3) (box-covering, laplacian RG) or O(N2)(geometric RG), our approach reduces it to O(N + E), where N is the number of nodes and E represents the number of edges, enabling our approach to compress networks of sizes that are unmanageable by other approaches. Therefore, our work demonstrates the feasibility of compressing large-scale networks.

Despite these advantages, our model still has limitations. While it can flexibly handle network structures from different domains, the statistical characteristics of networks also affect the model’s performance. Our experiments on more real network data have shown that denser networks are harder to preserve the partition function after compression. Furthermore, although we have proven that the model can preserve information flow, we cannot guarantee the preservation of all structural features. Experiments have shown that we can maintain the scale-free nature of the degree distribution after compressing BA networks, but we still cannot ensure the preservation of other important structural properties (see Supplementary Fig. 11 for related experiments).

Our work combines recent advances in the statistical physics of complex networks and machine learning to tackle one of the most formidable problems at the heart of complexity science: compression. Our findings highlight that to compress empirical networks it is required that nodes of similar local structures unify at different scales, behaving like vessels for the flow of information. Our fast and physically grounded compression method not only showcases the potential for application in a wide variety of disciplines where the flow within interconnected systems is essential, from urban transportation to connectomics, but also sheds light on the multiscale nature of information exchange between network’s components.

Methods

Training methodology

Our model is trained in a supervised learning manner, with our ultimate supervision objective being to ensure as much similarity as possible between the partition function curves of the macro and original networks. The partition function, a function of time, ultimately converges. In principle, we cannot directly compare and calculate losses between two functions. Therefore, we uniformly select ten points from the logarithmic interval of time before the partition function converges, composing a vector as the representation of the partition function. The aim is to minimize the Mean Absolute Error (MAE) between these two vectors.

In most scenarios, we also utilize another cross-entropy loss function to expedite the optimization process. Specifically, we randomly select two rows (indicating the grouping status of two nodes) from the grouping matrix and compute their cross-entropy, aiming to maximize this value as an alternative optimization objective. This loss function encourages the model to partition distinct nodes into separate supernodes, thereby accelerating the optimization process. The final loss function is determined by a weighted sum of this cross-entropy optimization objective and the similarity of the normalized partition functions, with different weights assigned to each.

Model parameter

In this section, we delineate the hyperparameters used during model training, enabling interested readers to reproduce our experimental results. Generally speaking, our model does not exhibit particular sensitivity towards hyperparameters.

  • Hyperparameter Settings for Network-Specific Compression Model

    • Epochs: we train the model for 15000 epochs until it converge;

    • Activation function: ReLU Function

    • Each layer learns an additive bias

    • Hidden neurons in GIN layer: 128

    • Num of layers in GIN: 1

    • Learning Rate: fixed to 0.001

    • Weight for loss functions: 0.99 for partition function loss and 0.01 for cross-entropy loss

  • Hyperparameter Settings for Compression Model for multiple networks

    • Epochs: we train the model for 3000 epochs until it converge;

    • Activation function: ReLU Function

    • Each layer learns an additive bias

    • Hidden neurons in GIN layer: 128

    • Num of layers in GIN: 1

    • Learning Rate: fixed to 0.001

    • Weight for loss functions: 0.99 for partition function loss and 0.01 for cross-entropy loss

Two target functions

Our model’s overall goal is to compress network size while ensuring the normalized partition function remains unchanged, with different normalization methods leading to different specific target functions. Assuming the original network has N nodes with a partition function Z, and the compressed network has \({N}^{{\prime} }\) nodes with a partition function \({Z}^{{\prime} }\), the two target functions are \(\frac{Z}{N}=\frac{{Z}^{{\prime} }}{{N}^{{\prime} }}\) and \(\frac{Z-1}{N-1}=\frac{{Z}^{{\prime} }-1}{{N}^{{\prime} }-1}\). Under all other equal conditions, the former target allows us to derive a relationship for the change in entropy as \({S}^{{\prime} }=S-log(N/{N}^{{\prime} })\), where \({S}^{{\prime} }\) denotes the entropy of the compressed graph, meaning the shape of the entropy curve remains unchanged after compression (see Supplementary Fig. 7 for numerical results). The latter ensures that the normalized results of the partition function range from 0 to 1, better preserving the original network’s eigenvalue distribution (see Supplementary Fig. 12 for experimental results). Unless otherwise specified, all results presented in the paper and supplementary materials are obtained under the first target function. We have also conducted experiments using the second target function; please refer to the Supplementary Fig. 13 for results on synthetic network compression results by the second target function. By setting different target functions, we have enriched the methods of network compression from different perspectives.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.