Abstract
Talc, as an important class of clay minerals constituting subducting oceanic crust, has long been known to undergo interlayer expansion by ~6% to contain net ~13 wt.% water into the ‘so-called’ 10 Å phase. Although subduction fluid is mildly alkaline and includes various salts and other dissolved species, its effect on the stability of subducting minerals has not yet been considered. Here, we report that subducting talc, when exposed to alkaline salty water conditions, breaks down to form a super-hydrated 15 Å phase at ~3.0 GPa and ~350 °C, corresponding to a depth of ~90–95 km along a cold subduction geotherm. The 15 Å phase remains stable down to ~125 km depth, where it transforms into the previously known 10 Å phase. Our combined experimental and computational results show that the super-hydrated 15 Å phase contains net ~31 wt.% water through interlayer expansion by ~60%. Our work thus demonstrates mineral transformation under more realistic subduction environments, which calls for reevaluation of subduction-related geochemistry and seismicity as well as water transportation into the deep Earth.
Similar content being viewed by others
Introduction
Subduction-related water transportation from the Earth’s surface to its deep interior is a pivotal process that fuels the Earth’s evolution and dynamics1,2. Current global subduction system transports ~7 – 10 × 1014 g/yr (or × 108 Tg/Myr) of water into the mantle in the form of structurally bound water (or hydroxyls) within various hydrous mineral phases contained in subducting slabs3,4. Experimental studies have established phase stabilities of major hydrous phases such as amphiboles, chlorite, serpentine, and dense hydrous magnesium silicates (DHMS), along diverse subduction thermal models3,5,6 where ca. 28.5% of the contemporary subduction has been categorized as cold system with a low thermal gradient of ~5–8 °C/km since ~800 Ma ago7,8,9,10. The stability of hydrous minerals depends on hydro-chemical processes as well as pressure-temperature (P-T) conditions, in most cases, resulting in liberation of structurally bound water in a range of subduction depths. The fluid chemistry along subducting slabs is then affected by exchange reactions with surrounding rocks while the fluid composition itself can cause changes in bulk rock composition, mineral assemblages, and mineral compositions under various chemical and physical conditions11. Therefore, it is a necessity to consider hydro-chemical characteristics of subduction zone fluids (SZFs) with respect to reactions and stabilities of subducting minerals. Salt and gas such as NaCl and CO2 are important components of the SZFs, together with dissolved silica, to affect the physical and chemical properties such as density, dielectric constant, and pH/alkalinity12,13,14. Subduction occurs initially in seawater-dominated fluid environment15 where the model calculated pH value is alkaline in the range of 8.08–8.33 due to bicarbonate ions [HCO3–]16,17. As such, the pH and alkalinity of the SZFs have been suggested as important variables in high-pressure and high-temperature (HP-HT) mineralogy and mantle geochemistry18,19,20,21. Recent studies employing theoretical and experimental approaches have further demonstrated that the pH of fluids in subducted crustal lithologies is moderately alkaline with the maximum changes of ΔpH up to ~2.3 along cold and intermediate P-T paths20,21,22.
In our previous work, we reported that albite (NaAlSi3O8), one of the most abundant minerals in the oceanic crust, breaks down into mono-layer hydrated smectite with interlayer spacing of ~12 Å (NaAl2(Si3Al)O10(OH)2·H2O) and moganite (SiO2) above ~2.5 GPa and 200 °C under water-containing cold subduction geotherm23. As the formation of the smectite assemblage from albite is accompanied by the release of OH- (and Na+) species into the region, alkaline fluids with as much as ΔpH of 2.2–2.5 have been postulated and linked to the mildly alkaline nature of SZFs23. This work called for the need to reevaluate the role of subducting fluid composition on the behavior of subducting minerals and their water transportation characteristics into the deep Earth. In this study, we have investigated the physicochemical properties and stability of subducting talc under controlled fluid compositions to simulate natural SZFs. As SZFs differ from pure water in terms of alkalinity, salts, dissolved silica, volatile contents, etc.12,20, fluid composition-dependent stability of talc would therefore provide more realistic insights into understanding subduction-related geochemistry, mineralogy, and related seismic and magmatic processes.
Talc (ideal composition, Mg3Si4O10(OH)2) is an important hydrous clay mineral in subduction-related environments since it commonly occurs as a metamorphic or hydrothermal alteration product in peridotite, basalt, and sediments constituting the oceanic lithosphere1,2,24,25,26,27,28. In terms of atomic structural arrangement, talc belongs to the 2:1 type layered silicate minerals (trioctahedral phyllosilicates) consisting of an Mg-octahedral (O) layer sandwiched by two Si-tetrahedral (T) layers (Supplementary Fig. 1). Because the OH- species, which account for ~4.75 wt.% of the hydration, are distributed in the central O-layer toward the vacant Si-tetrahedral site (Tv-site), the resulting tri-layer units (TOT ) are held together by weak van der Waals force to create cation- and water molecule-free interlayer with ~9.37 Å spacing. The interlayer d001-spacing of talc is non-expandable at ambient conditions, whereas it expands by ~6% to form the ‘so-called’ 10 Å phase (ideal composition, Mg3Si4O10(OH)2·nH2O, n = 0.65, 1.0, 2.0) via water intercalation in the P-T range of ~4–7 GPa and ~450–650 °C (refs. 29,30,31,32,33), corresponding to a ~ 125–220 km depth range in a cold subduction system. As such, the 10 Å phase with ~7.6–13.0 wt.% of water (counting both H2O and OH) has been proposed to be one of the major water carriers, together with other DHMS phases, down to the lower mantle30,31. This also led to the hypothesis that the MgO-SiO2-H2O (MSH) system could be a crucial chemical model for understanding the Earth’s mantle by about 85–90 wt.% in terms of its bulk composition32.
In this study, we have investigated in-situ phase stability and transformation of talc up to 7.7(3) GPa and 560 ± 30 °C using a resistively-heated diamond-anvil cell (RH-DAC) combined with synchrotron X-ray powder diffraction (XRD). We have applied cold subduction thermal gradients of ~5–8 °C/km (refs. 7,8,9,10), as modeled for the Kermadec and South Mariana subduction zones, and used salty and alkaline solutions that can be described in the Na2O-CO2-NaCl-H2O system to mimic natural subduction fluid compositions. Unlike previous results performed using pure water29,30,31,32,33, we observed the formation of a ‘super-hydrated’ 15 Å phase that contains ~8 times the amount of water in the original talc, together with magnesite, in the depth range between ~90 and ~125 km. This manifests a hydration reaction, which would call for reevaluation of the overall geochemical and geophysical models of subducting slabs and their surrounding regions.
Results
Hydration reaction of talc under modeled subduction fluids along cold subduction geotherm
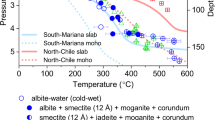
In-situ HP-HT synchrotron XRD experiments were performed on talc mixed with NaHCO3(l), NaCl(l), H2O(l), and CO2(g) in order to simulate diverse subduction fluid reactants in the Na2O-CO2-NaCl-H2O system (Fig. 1a, Supplementary Fig. 2, and Supplementary Table 1). Under alkaline salty water conditions using NaHCO3(l), talc breaks down into an expanded phase with the interlayer d001-spacing of 14.43(1) Å and magnesite (MgCO3) above 3.0(2) GPa and 350 ± 20 °C, corresponding to ~90–95 km depth along a cold subduction geotherm (Fig. 1b and Supplementary Fig. 2a). This phase assemblage remains stable up to 4.4(2) GPa and 470 ± 20 °C, corresponding to ~125 km depth, by which the interlayer d001-spacing of the expanded phase contracts gradually to 14.17(1) Å (Fig. 1b and Supplementary Table 2). Upon further increase in pressure and temperature above 5.3(3) GPa and 480 ± 20 °C, corresponding to ~165 km depth, the expanded phase transforms to the previously known 10 Å phase with the d001-spacing of 10.40(1) Å. The 10 Å phase then remains stable up to 5.8(4) GPa and 515 ± 30 °C, corresponding to ~180 km depth condition, by which its d001-spacing contracts gradually down to 9.76(1) Å. The 10 Å phase is recovered upon pressure and temperature release down to ambient condition with d001-spacing of ~10.30(1) Å. Based on the observed phase relationship of the expanded phase that forms between talc and its 10 Å phase under increasing depth conditions, we call the expanded phase ‘super-hydrated’ 15 Å phase that is expected to have a multi-layer hydration structure, compared to the mono-layer hydrated 10 Å phase.
a P-T stability of talc and its breakdown products under modeled subduction fluid along cold subdtion geotherms. The error bars represent pressure and temperature uncertainties (see Supplementary Table S1). Continuous and dashed curves denote the P-T paths of subducting slab surfaces and corresponding slab Moho, respectively, of two different cold subduction thermal models from Syracuse et al., 58. Black dashed lines represent previously established stability fields of talc29,30,83,84,85. b P-T dependent evolution of the basal d-spacing of talc under modeled subduction fluid along cold subduction geotherms. Each colored symbol represents talc under NaHCO3 solution (blue circle, purple circle for ex-situ), NaCl solution (yellow square), and H2O (green diamond). Phase abbreviations: Talc (Tlc), 10 Å phase (10 Å), super-hydrated 15 Å phase (15 Å), Enstatite (En), Magnesite (Mgs), Quartz (Qtz), Coesite (Cs) and Vapor/Fluid (V).
Grand canonical Monte Carlo (GCMC) simulations were conducted (see “Methods”, Fig. 2a, b) to estimate the interlayer water contents of hydrated talc phases with relative stabilities. As previous studies reported talc-like and phlogopite-like stacking modes for the 10 Å phase24,34, the two different staking modes were considered in the simulations. In the phlogopite-like stacking mode, basal oxygens of T-layers are superimposable across the interlayer (Fig. 2c), whereas the oxygens in the talc-like stacking mode are staggered across the interlayer (Fig. 2d). Based on the estimated water contents, three energy minima were identified in the interaction energy curves, mainly at d001-spacings of ~10, 12, and 15 Å, although the phlogopite-like model exhibited an additional minimum at 9.4 Å (Fig. 2a). The estimated water contents of hydrated talc phases at the apparent energy minima are ~9, ~19, and ~28 wt.% for interlayer H2O (or ~13, ~23, and ~31 wt.% including the intralayer OH species), respectively (Fig. 2b).
a Interlayer water content and interaction energy of hydrated talc phases as a function of basal d-spacing for two different stacking modes. b Density distribution of water (O atom) within the interlayer of 10, 12, and 15 Å phases of talc as calculated with NPT MD simulations (P = 3 GPa and T = 350 °C). c, d 2-D density distribution of H2O molecules and basal oxygens of Si tetrahedral (T) layers in (c) phlogopite-like 10 Å phase and (d) talc-like 10 Å phase averaged over 10 ns of MD simulations. Dashed hexagons represent two Si vacancy sites (Tv-site) of adjacent T-layers across the interlayer region. Black and red contours represent the basal oxygen positions of the adjacent T-layers. Blue and orange contours represent the O and H positions of water molecules, respectively. e, f and g MD simulation snapshots for each phase; (e) 9.4 Å phase, (f) 10 Å phase, and (g) super-hydrated 15 Å phase with density profile of its interlayer water (O atom) across the z-direction. Red rectangle and arrows indicate water bound to the vertically-oriented hydroxyls near the Tv-site via H-bonds. In the snapshot, yellow = Si tetrahedra, pink = Mg octahedra, red = O atoms, white = H atoms.
Molecular dynamics (MD) simulations were performed on those hydrated talc phases with relative stabilities. As expected, the hydroxyls in the central O-layer are modeled to be oriented toward the Tv-site in the basal T-layer. In the 10 Å phase, these hydroxyls form hydrogen-bonds by ~2.5 Å with intercalated H2O molecules in the interlayer while the dipole moments of the interlayer H2O are oriented almost vertically to the basal T-layer (Fig. 2e, f). Such an H2O bound to the Tv-site appears to be a unique feature in the water structure of hydrated talc phases formed at high pressure. In the phlogopite-like 10 Å phase (precisely d001 = 9.4 Å), interlayer H2O resides between a pair of upper and lower Tv-sites, forming a hydrogen-bond with only one of the two hydroxyls near the Tv-sites (Fig. 2e). In the talc-like 10 Å phase (precisely d001 = 10.5 Å), however, as the upper and lower Tv-sites are staggered, each hydroxyl near the Tv-site forms a hydrogen-bond with interlayer H2O (Fig. 2f). This configuration leads to two small peaks in the interlayer water density profile whereas the phlogopite-like 10 Å phase displays a single broad feature in the interlayer water density (Fig. 2b). It would, however, be reasonable to assign a single layer (1 W) hydration state for the 10 Å phases as the interlayer water molecules themselves lack hydrogen-bonded networks with intermolecular distances of ~5 Å. The H2O molecules bound to the hydroxyls near the Tv-sites were also identified in the 12 and 15 Å phases as small shoulder peaks in the water density profiles (Fig. 2g). Interlayer water molecules corresponding to the main peaks in the double-layer (2 W) and tri-layer (3 W) water densities of respective 12 and 15 Å phases are interconnected to form hydrogen-bonded networks with intermolecular distances of ~2.9 Å, featuring dynamic trajectories in their atomic positions. We suspect that the composition of fluid would affect further the formation and relative stabilities of the hydrated talc phases as our GCMC and MD simulations have not accounted for the effects of salts and/or alkalinity in the interlayer hydration.
In order to access the phase stability and evaluate the isothermal compressibility of the super-hydrated 15 Å phase, we have performed ex-situ HP-HT synchrotron XRD experiment under the same alkaline salty water condition using NaHCO3 solution up to 7.0(1) GPa (Supplementary Table 3 and Supplementary Fig. 3). The formation of the 15 Å phase assemblage from talc was observed at 3.8(1) GPa after heat treatment to 250 °C at 2.5(1) GPa (Supplementary Fig. 3), which was recovered to ambient condition to show the d001-spacing of ~15.22(1) Å for the uncompressed 15 Å phase (Supplementary Table 3). Isothermal compression at room temperature then showed gradual contraction of the d001-spacing for the 15 Å phase up to 7.0(1) GPa, which gave rise to a calculated linear compressibiliy (along the c-axis or d001-spacing) of β = 4.16 × 10−2 (GPa−1) for the 15 Å phase (Supplementary Fig. 4 and Supplementary Table 4). This value is about three and two times larger than those of the original talc and its 10 Å phase, respectively (refs. 35,36), which demonstrates that the 15 Å phase is potentially, also paradoxically, one of the most compressible minerals that forms under subduction environments. After the ex-situ experiment, we treated the recovered 15 Å phase with ethylene glycol solvation (C2H6O2) to examine its swelling property. As a result, the interlayer spacing has expanded to ~16.6 Å to confirm the smectite-like swelling feature of the super-hydrated 15 Å phase (Supplementary Fig. 5). Overall, the hydration reaction of talc under alkaline salty fluid condition along cold subduction geotherm can be summarized as follows:
To evaluate the role of CO2 in the Na2O-CO2-H2O fluid system, additional ex-situ HP-HT synchrotron XRD experiment was performed using talc under pure CO2 medium up to ~8 GPa and temperature treatment up to 300 °C. Unlike the hydration reaction observed in the Na2O-CO2-H2O fluid system, the formation of the super-hydrated 15 Å phase has not been observed as talc decomposed to form magnesite and quartz assemblage near 1.7(1) GPa after heating to 260 °C (Supplementary Fig. 2d). The dehydration breakdown scheme of talc in pure CO2 medium can be summarized as below:
Although most carbon-bearing geological fluids in the Earth’s mantle (at temperatures above 400 °C) exist as the C-O-H system, including species such as H2O, CO2, CH4, H2, CO, O2, and C2H6 (refs. 37,38), the reaction conditions (2) in our study would prefer the formation of magnesite (at temperatures below 400 °C), rather than the complex evolution of the fluid system itself. It has been known that magnesite is the major component of subducting carbonates to account for the carbon recycling through the deep mantle as its stability in the high pressure form extends to the lowermost mantle conditions, i.e., ~115 GPa and ~2100–2200 °C (ref. 39).
On the other hand, when NaCl solution or pure H2O are used as pressure transmitting medium along the similar P-T path, talc transforms directly to the 10 Å phase, as observed in the previous studies31,32,33, without transforming to the super-hydrated 15 Å phase assemblage (Fig. 1 and Supplementary Figs. 2b and 2c). The d001-spacing of the 10 Å phase formed under NaCl solution medium appears to be modulated to 9.51(1) Å at 4.8(2) GPa and 385 ± 20 °C, compared to 9.69(1) Å at 4.5(3) GPa and 420 ± 30 °C when formed under pure H2O medium (Fig. 1b and Supplementary Table 2), possibly due to the effect of dissolved salts on hydration network formation in the interlayer.
Discussion
Geological implications of the super-hydrated 15 Å phase
In a depth range of ~125–220 km along a water-containing cold subducting slab, talc has been known to undergo hydration by expanding its interlayer spacing by up to ~6.0%, i.e., from d(001) of 9.37 Å to d(001) of ~9.89–9.93 Å. This phase, previously named as the 10 Å phase, contains intercalated H2O molecules up to ~8.7 wt.% (or up to ~13.0 wt.% including the original OH)24,29,30,31,32,33,34,35. Under more realistic subduction fluid composition, i.e., under alkaline salty solution of pH ~8.3 by 0.5 M NaHCO3, we observed that talc decomposes into a phase assemblage consisting of the super-hydrated 15 Å phase and magnesite in a shallower depth range of ~90–125 km than the formation depth of the 10 Å phase. The appearance of the super-hydrated 15 Å phase (d(001) of ~15.2 Å when quenched to ambient conditions) indicates hitherto unknown hydration breakdown reaction while the formation of magnesite itself manifests a carbonation reaction.
In the case of smectite, which is built by the same 2:1 type trioctahedral layers such as talc but contains cations in the interlayer space, the correlation between the observed basal d(001) spacing and interlayer water contents has been established to be d(001) of ~18.3–18.9 Å for ~27 wt.% H2O in 3 W state, d(001) of ~14.4–15.8 Å for ~20 wt.% H2O in 2 W state, d(001) of ~12.0–12.6 Å for ~10 wt.% H2O in 1 W state, and d(001) of ~9.5–10.5 Å for dehydrated 0 W state40,41,42. However, the correlation between the water content and d-spacing should vary depending on the structural and chemical characteristics within and across the layers. According to our GCMC simulations, talc exhibits much smaller interlayer spacings than smectite-like interlayers at a given water content, i.e., ~28 wt.% H2O for ~15 Å interlayer spacing in the super-hydrated 15 Å phase vs. ~27 wt.% H2O for ~18.3–18.9 Å interlayer spacing in smectite. This is probably due to the P-T effect and the absence/presence of hydrated interlayer cations. Water density profiles obtained from our MD simulations show the super-hydrated 15 Å phase with ~28 wt.% H2O in 3 W state, potential 12 Å phase with ~19 wt.% H2O in 2 W state, and 10 Å phase with ~9 wt.% H2O in 1 W state (Fig. 2g). Based on the atomistic simulations, the super-hydrated 15 Å phase identified in the XRD experiments should correspond to the 3 W hydration state. We conjecture that the reason why the potential 12 Å phase in 2 W state has not been observed experimentally might be related to its limited stability at high temperatures as well as the different effects of dissolved salts and/or alkalinity in the course of the interlayer hydration, which needs further investigation.
Our experimentally observed 0 W to 3 W state hydration of talc, i.e., the formation of super-hydrated 15 Å phase, would account for absorbing ~8 times the amount of water contained in the original talc (i.e., hydroxyls), while subsequent transition from 3 W to 1 W state, i.e., partial dehydration to form the 10 Å phase, would be accompanied by releasing ~65% water (i.e., interlayer H2O) contained in the super-hydrated 15 Å phase (Fig. 3a). We have observed that the 1 W state of the 10 Å phase persists to ~180 km depth conditions, while the dehydration breakdown of the 10 Å phase has been reported to occur at ~690 °C in the pressure range of 5–7 GPa or with a negative dT/dP slope of ~80 °C/GPa in the higher pressure range up to ~10 GPa to form enstatite + coesite + fluids (MgSiO3 + SiO2 + H2O) assemblage43,44.
a The structural evolution of talc under modeled subduction fluid environment in cold subduction system: subducting talc (a, olive colored region) breakdowns into the super-hydrated 15 Å phase and magnesite assemblage in the depth range of ~90–125 km (b, pink colored region), followed by partial dehydration of the super-hydrated 15 Å phase into the 10 Å phase assemblage below ~165 km depth (c, brown colored region). b Estimations of H2O fluxes of subducting talc and global subducting slabs; boxes filled in pink and yellow are for subducting talc in cold and warm subduction zones, respectively, while boxes filled in navy are for global subducting slabs (based on the literature as summarized in Table 1). The boxes filled in light pink by dotted lines are enhanced estimations in the H2O fluxes to account the super-hydration and subsequent partial dehydration via the 15 Å phase (see Table 1 for the volatiles budget estimations). Depth ranges for subducting slab are shown in parenthesis. c H2O transport capacity of subducting talc compared to global subducting slabs by depths.
With regards to the source of water for the formation of the super-hydrated 15 Å phase in subduction environments, diverse cases of fluid generation, flow paths, and even local concentrations need to be assumed. One of the relevant processes is a dewatering in subduction zones that causes significant discharge of water into the overlying mantle45,46. Much of this fluid, however, is likely released at relatively shallow depths, escaping toward the surface. It has also been generally assumed that fluids migrate into the mantle wedge due to the vertically decreasing pressure. On the other hand, there are other perspectives on the migration pathways of subduction fluids, with potential deep fluid flow including upward migration, entrapment within the slab, updip migration along the slab, or even downward flow into deeper parts of the subducting slab47,48,49,50,51,52. For examples, hydrous fluids can originate from the dehydration of serpentinized lithosphere at depths between 120–200 km, migrating upward through the overlying mantle47. Some aqueous fluids may remain trapped within the subducting slab as free fluid or interstitial components, transported deeper into the mantle to depths beyond ~150 km48,49,50. Additionally, part of the released water could migrate updip along the slab51. Meanwhile, stress changes due to the bending of the oceanic plate could induce subhydrostatic or negative pressure gradients along normal faults, promoting downward fluid flow within the slab52. Therefore, we might infer that the released fluid does not simply disappear in the slab system; instead, it can be retained and redistributed through various processes within the system.
In modern subduction system, the H2O flux originating from hydrous minerals in the subducting slab has been estimated to be in the range of ~2.8 – 5.4 × 1014 g/yr (av. ~4.1 × 1014 g/yr) in a depth range of 100–150 km, which decreases to ~2.2 – 3.4 × 1014 g/yr (av. ~2.8 × 1014 g/yr) in a deeper region of 150–230 km as a result of (partial) dehydration4 (Fig. 3b). Based on the estimated amount of talc in the oceanic crust, i.e., < ~5–20 vol %, the initial H2O flux contributed through talc can be estimated to be ~0.73 – 2.6 × 1014 g/yr (av. ~1.7 × 1014 g/yr) (Fig. 3b, Table 1 and references therein). By assuming that in cold subduction zones, the subducting talc undergoes super-hydration to the 15 Å phase as observed in this study, we can re-evaluate the H2O flux of subducting slab down to ~300 km depth. From the depth of ~90 km, the water contents transported by talc would increase via the formation of the 15 Å phase by ~770% (ca. 8 folds) from ~0.42 – 1.5 × 1022 g H2O to ~0.36–1.3 × 1023 g H2O, i.e., from av. ~0.48 × 1014 g H2O/yr to ~4.2 × 1014 g H2O/yr (Fig. 3b and Table 1). This requires reevaluation of the H2O flux by global subducting slabs from av. ~4.1 × 1014 g H2O/yr to ~7.8 × 1014 g H2O/yr in the intermediate depth range of ~90–150 km, which leads to an increase in the H2O transport capacity of subducting talc from ~5.6% to ~53.5% (Fig. 3c). Such an estimated amount of the H2O uptake is ~0.32 – 1.2 × 1023 g, which may be translated to ~85 – 310 m of sea level reduction (or ~2.3 – 8.3% of global ocean) over 200 Ma (Table 1). While the super-hydrated 15 Å phase remains stable down to ~125 km depth, the partial dehydration from the 15 Å to 10 Å phase would occur in the depths below ~165 km to release ~2.4 – 8.6 × 1022 g of H2O to the surrounding mantle, which is equivalent to ~1.2 – 4.3 × 1014 g H2O/yr (or ~1.7–6.1% of global ocean) over 200 Ma (Table 1).
The H2O transportation along subduction zones affects arc magmatism and earthquakes51,53. Specifically, arc magma generation is controlled by the dehydration reactions of subducting hydrous minerals54,55, which is in turn influenced by subduction-related factors such as slab age, convergence rate, and slab dip56, together with other thermal characteristics of the subduction zone57. In order to find any correlations between the stability of subducting talc-related phases and subduction volcanism and seismicity, we have compiled the depths to the top of the slab beneath volcano (H) using volcano-specific subduction parameters of the global arc system at 298 volcanic centers above cold subductions (data from Syracuse and Abers, ref. 58). As a result, ~25% of volcanoes located above 15 cold subduction zones have H values within the range from 125 to 175 km (Fig. 4a). More specifically, for volcanoes above the South Mariana subduction zones, for which we modeled the P–T path of subducting talc, the H value is estimated to be ~134 km, for which the corrected H values (Hcorr) become ~156 km (Fig. 4a) after accounting for hypocenter errors. In this study, we showed that super-hydration of subducting talc would occur in the depth range of ~90–125 km while the partial dehydration of the super-hydrated 15 Å phase to the 10 Å phase would occur near ~165 km. Given the apparent correlation between the corrected slab depths beneath arc volcanoes and our experimental results, we speculate that the dehydration of the super-hydrated 15 Å phase may partially be contributing to the arc magma generation.
a Volcanoes in the South Mariana and other cold subduction systems using volcano-specific subducion parameters of the global arc system at 298 volcanic centers (data from Syracuse and Abers (2006)). The number of volcanoes along 15 cold subduction zones is shown by H (depths to the top of the slab beneath volcano) intervals of ~25 km in the right panel. b Earthquake distribution in the South Mariana subduction systems over the past 20 years using data from the International Seismological Center (2024), ISC-EHB dataset86,87,88. The depth-dependent earthquake frequency (in intervals of ~25 km) is shown in the right panel.
Furthermore, intermediate-depth seismicity in subduction zones is known to be induced by mechanisms such as dehydration embrittlement59, phase transformation60, hydration61, stress transfer62, and thermal runaway instabilities63. To find correlations of our observations to the seismicity of subduction zones, we have plotted the distribution of seismic frequencies along the South Mariana subduction zones (Fig. 4b). We find that the earthquake frequencies decrease by ~44% in the depth range of 75–125 km, which overlaps with the formation depth of the super-hydrated 15 Å phase ( ~ 90–125 km). On the other hand, the earthquake frequencies increase by ~34% in the depth range of 150–200 km, which appears to be correlated to the partial dehydration depth of the super-hydrated 15 Å phase ( ~ 165 km depth).
In summary, we have found a mineral breakdown reaction that facilitates water transport into the Earth’s interior. By taking into account the chemical and thermal characteristics of contemporary subduction system, the efficiency of water transport can be significantly revised to be enhanced via the formation of the super-hydrated 15 Å phase where carbonation reaction co-operates. Considerations on such complex nature of mineral-fluid interactions under realistic subduction environments are necessary to deepen our understanding of subduction-related volcanism and seismicity as well as volatile transport and cycling into the Earth’s interior.
Methods
Sample and initial characterization
Initial characterization of talc (The Smithsonian Institution, NMNH B17990/ IGSN NHB0027G4, Falkenkoepfle, Zillertal Valley, Tirol, Austria) used in this study was performed using X-ray diffraction (XRD) and field emission scanning electron microscope (FE-SEM, JEOL-7800F) equipped with energy-dispersive spectrometer (EDS, Oxford Instruments) (Supplementary Fig. 1). The chemical composition and morphology on talc were identified by using scanning electron microscopy (SEM) and energy dispersive spectroscopy (EDS). SEM images of talc show layered morphology while the calculated chemical formula from semi-quantified EDS results is derived to be (Mg3-x,Fex)Si4O10(OH)2 with x < 0.05. The XRD pattern on talc was indexed as space group C-1 with refined cell parameters of a = 5.3172(9) Å, b = 9.1666(6) Å, c = 9.4890(15) Å, α = 90.779(11) °, β = 99.064(14) °, γ = 89.923(8) °.
We have performed ex-situ and in-situ high-pressure and high-temperature synchrotron X-ray diffraction experiments to investigate the stability of talc in the Na2O-CO2-NaCl-H2O system using sodium bicarbonate (NaHCO3, 0.5 M, pH ~8.3) and sodium chloride (NaCl, 0.5 M) solutions as pressure-transmitting fluid (PTM).
Ex-situ high-pressure and high-temperature synchrotron x-ray powder diffraction
Ex-situ synchrotron X-ray powder diffraction measurements on talc under NaHCO3 and CO2 medium were performed using symmetric diamond anvil cell (DAC) at beamline 6D UNIST-PAL of Pohang Light Source-II (PLS-II) and at beamline BL10-2 of Stanford Synchrotron Radiation Lightsource (SSRL), respectively. At beamline 6D, the X-ray beam from the bending magnet was tuned to a wavelength of 0.653 Å (18.986 keV) and a beam size of 200 × 200 μm2. A 2D CCD detector (MX225-HS, Rayonix L.L.C., USA) was used to collect diffraction data at ~231 mm from the sample using 100 sec exposure time. At beamline BL10-2, the X-ray beam from the wiggler was tuned to a wavelength of 0.61992 Å (20.0 keV) and a beam size of 100 × 100 μm2. A Pilatus 300K-w Si-diode CMOW detector was used to collect diffraction data at ~1114 mm from the sample to cover 2-theta range of up to 30 ° for 200 sec exposure time. A symmetric-type DAC with culet diameter of 500 µm was used as a high-pressure vessel. A stainless-steel gasket of 250 µm in thickness was indented to ca. 80 µm, and a hole of ca. 250 µm in diameter was drilled in the center as a sample chamber using an electric discharge machine. For NaHCO3 medium run, the powdered talc sample was loaded with sodium bicarbonate solution (NaHCO3, 0.5 M, pH ~8.3) into the gasket hole with a few ruby spheres of several microns in size as pressure marker. The sample was then pressurized up to ~7 GPa while the temperature was applied ex-situ by placing the DAC in a furnace at ca. 250 °C for 24 h. For CO2 PTM run, the powdered talc sample was loaded with CO2 under liquid-nitrogen cooled condition into the gasket hole with a few ruby spheres as pressure marker. The sample was then compressed up to ~5 GPa while the temperature was applied ex-situ by placing the DAC in a furnace at ca. 260 °C for 2 h.
In-situ high-pressure and high-temperature synchrotron x-ray powder diffraction
In-situ synchrotron X-ray powder diffraction measurements were performed at 3D-XRS beamline at PLS-II, South Korea, 13-BMC beamline at Advanced Photon Source (APS), USA, and the Extreme Conditions Beamline (ECB) P02.2 at PETRA-III, Germany, as previously decribed in Hwang et al. 23. At beamline 3D, the X-ray beam from the bending magnet was tuned to a wavelength of 0.6888(1) Å (18.0 keV) or 0.6877(1) Å (18.03 keV) and beam size of 100 × 100 μm2. A Mar345 image plate detector was used to collect diffraction data at a distance of 315.7 mm from the sample with 200 sec exposure time. At beamline 13-BMC, the X-ray beam from the bending magnet source was tuned to a wavelength of 0.4340(1) Å (28.568 keV) and focused to 12 × 18 μm2 in size (FWHM) using a KB-mirror. A PILATUS 1 M detector was used to collect diffraction data at distance of ~169 mm from the sample with 150 sec of exposure time. At beamline P02.2, the X-ray beam from the undulator source was tuned to a wavelength of 0.4845(1) Å (25.590 keV) and focused to 8 × 4 μm2 in size (FWHM) using Compound Refractive Lense (CRL) optics. A Perkin Elmer XRD 1621 detector was used to collect diffraction data at distance of ~404 mm from the sample with 10 sec of exposure time. As a pressure vessel, symmetric-type DAC with culet diameter of 500 µm was used. A stainless-steel gasket of 250 µm in thickness was indented to ca. 40–60 µm, and a hole of ca. 250 µm in diameter was drilled in the center as a sample chamber using an electric discharge machine. Simultaneous P-T condition was created by the combination of a membrane device for online pressure control and a resistive electrical heater (a coil heater (at PLS and APS) and a graphite foil heater (at PETRA-III)) surrounding the diamond anvils. The coil heater was made of a kanthal (iron-chromium-aluminum alloys) wire of 0.45 mm in diameter with 2.2 Ω resistance. The graphite foil heater was made of a flexible graphite sheet of 0.5 mm in thickness with ~0.3 Ω resistance (A more detailed description of graphite RH-DAC setup can be found in the literature64). Temperature was monitored using a K-type or a R-type thermocouple attached to the pavilion of the diamond anvil close to the sample, which allowed the maximum uncertainties of ± 30 °C. Pressure was calculated using the equation of state of Au or Cu pressure marker65,66 included in the sample chamber. Initially, we compressed the sample to ~1.0–2.0 GPa and then increased the pressure and temperature in increments of ~0.5 GPa and 50 °C up to ~7.7 GPa and ~560 °C, respectively (Supplementary Table 1).
Atomistic simulations of hydrated talc phases
Talc crystal structures were constructed by expansion of the experimental unit cell structure67 to a 5 × 3 × 2 supercell (a = 26.30 Å, b = 27.30 Å, c = 18.81 Å, α = γ = 90°, β = 100°). For hydrated talc phases, H2O molecules were inserted to the interlayer of the pure talc supercell in two forms of TOT layer stacking, i.e., talc-like and phlogopite-like stacking modes. The CLAYFF force field68 was used to describe the interatomic potential of talc, and the SPC/E potential69 was used for water molecules. The Lorentz-Berthelot combination rule was applied to the potential between heteroatoms70. For evaluation of the maximum water contents of talc at given d-spacings, GCMC simulations were performed using the GIBBS code71. The chemical potential of the water reservoir corresponding to the state of 3 GPa and 350 °C was determined by the Widom insertion test of bulk water72. We performed an equilibrium run of 20 million MC steps and a production run of 100 million MC steps at the fixed chemical potential. Insertion or deletion of water molecules was attempted with a probability of 70%, translation with a probability of 15%, and rotation with a probability of 15%. The interaction energies between talc and intercalating water, calculated corresponding to the maximum water contents, are reported per water molecule. MD simulations were performed with NPT ensemble (350 °C, 3 GPa) for hydrated talc phases based on the water contents determined by GCMC simulations. We used the LAMMPS code73, with an equilibrium run for 1 ns and a production run for 10 ns. The temperature and pressure were controlled using Nosé-Hoover chain thermostats74,75. For long-range electrostatics, Ewald summation with an accuracy of 0.0001 kcal/mol was applied76. The SHAKE algorithm was used to maintain the rigidity of SPC/E water77. Additional simulations were performed at 470 °C and 4.4 GPa, but no significant differences between the phases were observed.
Data availability
All the data generated in this study are available within the Article, Supplementary Information, or Source Data file. Source data is deposited in the figshare repository (https://doi.org/10.6084/m9.figshare.27316125). Any additional data are available from the corresponding author upon request.
Code availability
All data presented in this manuscript were obtained without the use of custom code.
References
Schmidt, M. W. & Poli, S. 4.19 - Devolatilization During Subduction. Treatise on Geochemistry (Second Edition), 669–701 (2014).
Faccenda, M. Water in the slab: a trilogy. Tectonophysics 614, 1–30 (2014).
Ohtani, E. Water in the mantle. Elements 1, 25–30 (2005).
van Keken, P. E., Hacker, B. R., Syracuse, E. M. & Abers, G. A. Subduction factory 4. depth-dependent flux of H2O from subducting slabs worldwide. J. Geophys. Res. Solid Earth 116, B01401 (2011).
Grove, T. L., Chatterjee, N., Parman, S. W. & Médard, E. The influence of H2O on mantle wedge melting. Earth Planet. Sci. Lett. 249, 74–89 (2006).
Hacker, B. R. H2O subduction beyond arcs. Geochem. Geophys. Geosyst. 9, Q03001 (2008).
Korenaga, J. Urey ratio and the structure and evolution of Earth’s mantle. Rev. Geophys. 46, RG2007 (2008).
Ganne, J. & Feng, X. Primary magmas and mantle temperatures through time. Geochem. Geophys. Geosyst. 18, 872–888 (2017).
Weller, M. B. & Lenardic, A. On the evolution of terrestrial planets: bi-stability, stochastic effects, and the non-uniqueness of tectonic states. Geosci. Front. 9, 91–102 (2018).
Palin, R. M. et al. Secular change and the onset of plate tectonics on Earth. Earth-Sci. Rev. 207, 103172 (2020).
Dolejš, D. & Wagner, T. Thermodynamic modeling of non-ideal mineral–fluid equilibria in the system Si–Al–Fe–Mg–Ca–Na–K–H–O–Cl at elevated temperatures and pressures: Implications for hydrothermal mass transfer in granitic rocks. Geochim. Cosmochim. Acta 72, 526–553 (2008).
Manning, C. E. & Frezzotti, M. L. Subduction-zone fluids. Elements 16, 395–400 (2020).
Keppler, H. Fluids and trace element transport in subduction zones. Am. Mineral. 102, 5–20 (2017).
Frezzotti, M. L. & Ferrando, S. The chemical behavior of fluids released during deep subduction based on fluid inclusions. Am. Mineral. 100, 352–377 (2015).
Holland, G. & Ballentine, C. J. Seawater subduction controls the heavy noble gas composition of the mantle. Nature 441, 186–191 (2006).
Marion, G. M. et al. pH of seawater. Mar. Chem. 126, 89–96 (2011).
Middelburg, J. J., Soetaert, K. & Hagens, M. Ocean alkalinity, buffering and biogeochemical processes. Rev. Geophys. 58, e2019RG000681 (2020).
De Hoog, J. C. M. & Savov, I. P. Boron Isotopes as a Tracer of Subduction Zone Processes. (ed Marschall, H., Foster, G.) in Boron Isotopes: The Fifth Element. 217-247 (Springer International Publishing: Cham, 2018).
Mottl, M. J., Wheat, C. G., Fryer, P., Gharib, J. & Martin, J. B. Chemistry of springs across the Mariana forearc shows progressive devolatilization of the subducting plate. Geochim. Cosmochim. Acta 68, 4915–4933 (2004).
Galvez, M. E., Connolly, J. A. D. & Manning, C. E. Implications for metal and volatile cycles from the pH of subduction zone fluids. Nature 539, 420 (2016).
Mikhail, S., Barry, P. H. & Sverjensky, D. A. The relationship between mantle pH and the deep nitrogen cycle. Geochim. Cosmochim. Acta 209, 149–160 (2017).
Li, H.-Y. et al. Molybdenum isotopes unmask slab dehydration and melting beneath the Mariana arc. Nat. Commun. 12, 6015 (2021).
Hwang, G. C. et al. A role for subducted albite in the water cycle and alkalinity of subduction fluids. Nat. Commun. 12, 1155 (2021).
Fumagalli, P., Stixrude, L., Poli, S. & Snyder, D. The 10Å phase: a high-pressure expandable sheet silicate stable during subduction of hydrated lithosphere. Earth Planet. Sci. Lett. 186, 125–141 (2001).
Ohtani, E., Litasov, K., Hosoya, T., Kubo, T. & Kondo, T. Water transport into the deep mantle and formation of a hydrous transition zone. Phys. Earth Planet. Inter. 143-144, 255–269 (2004).
Ulmer, P & Trommsdorff, V. Phase relations of hydrous mantle subducting to 300 km. In Mantle petrology: Field observations and high pressure experimentation. Geochem. Soc. Spec. Publ. 6, 259–281 (1999).
Liou, J. G. & Zhang, R. Y. Significance of ultrahigh-P talc-bearing eclogitic assemblages. Mineralogical Mag. 59, 93–102 (1995).
Chopin, C. Talc-Phengite: a widespread assemblage in high-grade pelitic blueschists of the western alps. J. Petrol. 22, 628–650 (1981).
Chinnery, N. J., Pawley, A. R. & Clark, S. M. In situ observation of the formation of 10 Å phase from Talc + H2O at mantle pressures and temperatures. Science 286, 940–942 (1999).
Pawley, A. R. & Wood, B. J. The high-pressure stability of talc and 10 Å phase: potential storage sites for H2O in subduction zones. Am. Mineral. 80, 998–1003; (1995).
Yamamoto, K. & Akimoto, S. The system MgO-SiO2-H2O at high pressures and temperatures; stability field for hydroxyl-chondrodite, hydroxyl-clinohumite and 10 A o-phase. Am. J. Sci. 277, 288–312 (1977).
Wunder, B. & Schreyer, W. Metastability of the 10-Å phase in the system MgO–SiO2–H2O (MSH). what about hydrous MSH phases in subduction zones? J. Petrol. 33, 877–889 (1992).
Bauer, J. F. & Sclar, C. B. The” 10A phase” in the system MgO-SiO2-H2O. Am. Mineral. 66, 576–585 (1981).
Comodi, P., Fumagalli, P., Nazzareni, S. & Zanazzi, P. F. The 10 Å phase: crystal structure from single-crystal X-ray data. Am. Mineral. 90, 1012–1016 (2005).
Gleason, A. E., Parry, S. A., Pawley, A. R., Jeanloz, R. & Clark, S. M. Pressure-temperature studies of talc plus water using X-ray diffraction. Am. Mineral. 93, 1043–1050 (2008).
Comodi, P., Cera, F., Dubrovinsky, L. & Nazzareni, S. The high-pressure behaviour of the 10 Å phase: a spectroscopic and diffractometric study up to 42 GPa. Earth Planet. Sci. Lett. 246, 444–457 (2006).
Huizenga, J.-M. Thermodynamic modelling of C–O–H fluids. Lithos 55, 101–114 (2001).
Zhang, C. & Duan, Z. A model for C–O–H fluid in the Earth’s mantle. Geochim. Cosmochim. Acta 73, 2089–2102 (2009).
Isshiki, M. et al. Stability of magnesite and its high-pressure form in the lowermost mantle. Nature 427, 60 (2004).
Suquet, H., de la Calle, C. & Pezerat, H. Swelling and structural organization of saponite. Clays Clay Min. 23, 1–9 (1975).
Colton-Bradley, V. Role of pressure in smectite dehydration—effects on geopressure and smectite-to-illite transition. AAPG Bull. 71, 1414–1427 (1987).
Hüpers, A. & Kopf, A. J. Effect of smectite dehydration on pore water geochemistry in the shallow subduction zone: An experimental approach. Geochem. Geophys. Geosyst. 13, https://doi.org/10.1029/2012GC004212 (2012).
Pawley, A. R., Chinnery, N. J., Clark, S. M. & Walter, M. J. Experimental study of the dehydration of 10-Å phase, with implications for its H2O content and stability in subducted lithosphere. Contrib. Mineral. Petrol. 162, 1279–1289 (2011).
Rashchenko, S. V., Kamada, S., Hirao, N., Litasov, K. D. & Ohtani, E. In situ X-ray observation of 10 Å phase stability at high pressure. Am. Mineral. 101, 2564–2569 (2016).
Peacock, S. M. Fluid processes in subduction zones. Science 248, 329–338 (1990).
Bebout, G. E. & Barton, M. D. Metasomatism during subduction: products and possible paths in the Catalina Schist. Calif. Chem. Geol. 108, 61–92 (1993).
Ulmer, P. & Trommsdorff, V. Serpentine stability to mantle depths and subduction-related magmatism. Science 268, 858 (1995).
Bruce Watson, E. & Lupulescu, A. Aqueous fluid connectivity and chemical transport in clinopyroxene-rich rocks. Earth Planet. Sci. Lett. 117, 279–294 (1993).
Mibe, K., Yoshino, T., Ono, S., Yasuda, A. & Fujii, T. Connectivity of aqueous fluid in eclogite and its implications for fluid migration in the Earth’s interior. J. Geophys. Res. Solid Earth 108, 2295 (2003).
Scambelluri, M. & Philippot, P. Deep fluids in subduction zones. Lithos 55, 213–227 (2001).
Hacker, B. R., Peacock, S. M., Abers, G. A. & Holloway, S. D. Subduction factory 2. Are intermediate‐depth earthquakes in subducting slabs linked to metamorphic dehydration reactions? J. Geophys. Res. Solid Earth 108, 2030 (2003).
Faccenda, M., Gerya, T. V. & Burlini, L. Deep slab hydration induced by bending-related variations in tectonic pressure. Nat. Geosci. 2, 790–793 (2009).
Grove, T. L., Till, C. B. & Krawczynski, M. J. The role of H2O in subduction zone magmatism. Annu. Rev. Earth. Pl. Sc. 40, 413–439 (2012).
Tatsumi, Y. Formation of the volcanic front in subduction zones. Geophys. Res. Lett. 13, 717–720 (1986).
Kerrick, D. M. & Connolly, J. A. D. Metamorphic devolatilization of subducted oceanic metabasalts: implications for seismicity, arc magmatism and volatile recycling. Earth Planet. Sci. Lett. 189, 19–29 (2001).
England, P., Engdahl, R. & Thatcher, W. Systematic variation in the depths of slabs beneath arc volcanoes. Geophys. J. Int. 156, 377–408 (2004).
England, P. & Wilkins, C. A simple analytical approximation to the temperature structure in subduction zones. Geophys. J. Int. 159, 1138–1154 (2004).
Syracuse, E. M. & Abers, G. A. Global compilation of variations in slab depth beneath arc volcanoes and implications. Geochem. Geophys. Geosyst. 7, n/a–n/a (2006).
Jung, H., Green, H. W. II & Dobrzhinetskaya, L. F. Intermediate-depth earthquake faulting by dehydration embrittlement with negative volume change. Nature 428, 545–549 (2004).
Green, H. W. II, Shi, F., Bozhilov, K., Xia, G. & Reches, Z. Phase transformation and nanometric flow cause extreme weakening during fault slip. Nat. Geosci. 8, 484–489 (2015).
Barcheck, C. G., Wiens, D. A., van Keken, P. E. & Hacker, B. R. The relationship of intermediate- and deep-focus seismicity to the hydration and dehydration of subducting slabs. Earth Planet. Sci. Lett. 349-350, 153–160 (2012).
Ferrand, T. P. et al. Dehydration-driven stress transfer triggers intermediate-depth earthquakes. Nat. Commun. 8, 15247 (2017).
Braeck, S. & Podladchikov, Y. Y. Spontaneous thermal runaway as an ultimate failure mechanism of materials. Phys. Rev. Lett. 98, 095504 (2007).
Hwang, H. et al. Graphite resistive heated diamond anvil cell for simultaneous high-pressure and high-temperature diffraction experiments. Rev. Sci. Instrum. 94, 083903 (2023).
Anderson, O. L., Isaak, D. G. & Yamamoto, S. Anharmonicity and the equation of state for gold. J. Appl. Phys. 65, 1534–1543 (1989).
Tsuchiya, T. First-principles prediction of the P-V-T equation of state of gold and the 660-km discontinuity in Earth’s mantle. J. Geophys. Res. Solid Earth 108, 2462 (2003).
Gruner, J. W. The crystal structures of talc and pyrophyllite. Z. f. ür. Kristallographie - Crystalline Mater. 88, 412–419 (1934).
Cygan, R. T., Liang, J.-J. & Kalinichev, A. G. Molecular models of hydroxide, oxyhydroxide, and clay phases and the development of a general force field. J. Phys. Chem. B 108, 1255–1266 (2004).
Berendsen, H. J. C., Grigera, J. R. & Straatsma, T. P. The missing term in effective pair potentials. J. Phys. Chem. 91, 6269–6271 (1987).
Halgren, T. A. The representation of van der Waals (vdW) interactions in molecular mechanics force fields: potential form, combination rules, and vdW parameters. J. Am. Chem. Soc. 114, 7827–7843 (1992).
Mackie, A. D., Tavitian, B., Boutin, A. & Fuchs, A. H. Vapour-liquid phase equilibria predictions of methane–alkane mixtures by Monte Carlo simulation. Mol. Simul. 19, 1–15 (1997).
Widom, B. Some topics in the theory of fluids. J. Chem. Phys. 39, 2808–2812 (1963).
Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Computational Phys. 117, 1–19 (1995).
Martyna, G. J., Tuckerman, M. E., Tobias, D. J. & Klein, M. L. Explicit reversible integrators for extended systems dynamics. Mol. Phys. 87, 1117–1157 (1996).
Shuichi, N. Constant temperature molecular dynamics methods. Prog. Theor. Phys. Suppl. 103, 1–46 (1991).
Karasawa, N. & Goddard, W. A. III Acceleration of convergence for lattice sums. J. Phys. Chem. 93, 7320–7327 (1989).
Ryckaert, J.-P., Ciccotti, G. & Berendsen, H. J. C. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Computational Phys. 23, 327–341 (1977).
White, R. S., McKenzie, D. & O’Nions, R. K. Oceanic crustal thickness from seismic measurements and rare earth element inversions. J. Geophys. Res. Solid Earth 97, 19683–19715 (1992).
Geissler, W. H., Jokat, W., Jegen, M. & Baba, K. Thickness of the oceanic crust, the lithosphere, and the mantle transition zone in the vicinity of the Tristan da Cunha hot spot estimated from ocean-bottom and ocean-island seismometer receiver functions. Tectonophysics 716, 33–51 (2017).
Straume, E. O. et al. GlobSed: updated total sediment thickness in the world’s oceans. Geochem. Geophys. Geosyst. 20, 1756–1772 (2019).
Vine, F. J. & Moores, E. M. A Model for the Gross Structure, Petrology, and Magnetic Properties of Oceanic Crust. (ed Shagam, R. et al.) in Studies in Earth and Space Sciences, 132 (Geological Society of America, 1972).
Wyllie, P. J. The Dynamic Earth: textbook in geosciences. 139–165 (John Wiley & Sons, Inc.: New York (1971).
Johannes, W. An experimental investigation of the system MgO-SiO2-H2O-CO2. Am. J. Sci. 267, 1083–1104 (1969).
Jenkins, D. M., Holland, T. J. B. & Clare, A. K. Experimental determination of the pressure-temperature stability field and thermochemical properties of synthetic tremolite. Am. Mineral. 76, 458–469 (1991).
Boyd, F. R. & England, J. L. The quartz-coesite transition. J. Geophys. Res. 65, 749–756 (1960).
Engdahl, E. R., van der Hilst, R. & Buland, R. Global teleseismic earthquake relocation with improved travel times and procedures for depth determination. Bull. Seismological Soc. Am. 88, 722–743 (1998).
Weston, J., Engdahl, E. R., Harris, J., Di Giacomo, D. & Storchak, D. A. ISC-EHB: reconstruction of a robust earthquake data set. Geophys. J. Int. 214, 474–484 (2018).
Engdahl, E. R. et al. ISC-EHB 1964–2016, an improved data set for studies of earth structure and global seismicity. Earth Space Sci. 7, e2019EA000897 (2020).
Acknowledgements
This work was supported by the Leader Researcher program of the Korean Ministry of Science and ICT (NRF-2018R1A3B1052042). Y.B. acknowledges the support by the Institute for Korea Spent Nuclear Fuel (iKSNF) and National Research Foundation of Korea (NRF) grant funded by the Korea government (Ministry of Science and ICT, MSIT) (No.2021M2E1A1085186) for the work performed at KAERI. K.D.K. thanks the support by the Korean Ministry of Education (NRF-No.2019R1A6A1A03033167), and D.Z. acknowledges the support by the National Science Foundation (EAR−1634415 and EAR-1661511). Synchrotron experiments were performed at beamline BL10-2 at SSRL, the beamlines 3D and 6D at PLS-II, PAL, beamline 13-BMC at APS, and beamline ECB P02.2 at PETRA-III at Deutsches Elektronen-Synchrotron (DESY, Hamburg, Germany), a member of the Helmholtz Association HGF. We also acknowledge the scientific exchange and support of the Center for Molecular Water Science (CMWS) at DESY.
Author information
Authors and Affiliations
Contributions
Y.B. and Y.L. conceived and designed the research. Y.B. performed synchrotron experiments and data analysis with the help from J.C., H.S., D.Z, T.-Y.J., T.J.S., and H.-P.L. J.K. and K.D.K performed atomistic simulations. Y.B., J.K., K.D.K., and Y.L. wrote the initial draft of the manuscript. Y.L. supervised the research and worked on the manuscript with all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Stefano Poli, and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Bang, Y., Kim, J., Choi, J. et al. Formation of the 15 Å phase as the most expanded hydrated mineral in cold subduction zone. Nat Commun 16, 2279 (2025). https://doi.org/10.1038/s41467-025-56672-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-025-56672-6