Abstract
Next generation sequencing reads from RNA-seq studies expose private genotypes of individuals during computation. Here, we introduce pQuant, an algorithm that employs homomorphic encryption to ensure privacy-preserving quantification of gene expression from RNA-seq data across public and cloud servers. pQuant performs computations on encrypted data, allowing researchers to handle sensitive information without exposing it. Our evaluations demonstrate that pQuant achieves accuracy comparable to state-of-the-art non-secure algorithms like STAR and kallisto. pQuant is highly scalable and its runtime and memory do not depend on the number of reads. It also supports parallel processing to enhance efficiency regardless of the number of genes analyzed.
Similar content being viewed by others
Introduction
The ability to survey the personal transcriptome of patients has given researchers the power to interpret the functional elements of their genome, reveal the molecular constituents of their cells and tissues, and eventually connect their genetics to the molecular mechanisms underlying disease and development1. However, deciphering personal transcriptomics data to make connections to phenotypic consequences requires widespread access to data, which, in turn, is often in conflict with the increasing need to protect patient privacy. This issue is complicated by differences in the international regulatory landscape (e.g., GDPR vs. HIPAA), which can restrict data access to varying degrees. Institutional policies further restrict access in response to rising health data breaches and new privacy threats, such as the statistical linking of datasets to deduce an individual’s involvement in sensitive studies such as those investigating drug abuse2,3,4,5. Moreover, the rapid growth of data and computational requirements are challenging the use of local servers when data is collected from thousands of individuals in consortium settings. Therefore, there is a push towards cloud computing, which has the potential to further erode the privacy of research participants.
RNA-seq generates next-generation sequencing (NGS) reads that are composed of parts of personal genomic sequences of the expressed genes of the patients that samples are taken from6,7. These private genotypes are exposed during the quantification of gene expression from NGS reads. A major consequence of not solving these private information exposures is siloing datasets behind firewalls, creating administrative hurdles for scientists who could otherwise combine datasets and generate important biological knowledge from the data. Here we address this issue by creating a privacy-enhancing RNA-seq processing tool for quantification of gene expression (Fig. 1). This tool enables researchers to operate on data without ever revealing the content of the input and output during computation. We achieve this by using homomorphic encryption, which allows computations on encrypted data and provides mathematical guarantees for security. Note that this study focuses on addressing the challenges of responsibly accessing and processing data in cloud environments, rather than facilitating data sharing across institutions. Nevertheless, our tools can also be adapted for data-sharing protocols by leveraging shared encryption keys and enabling the secure exchange of secret keys.
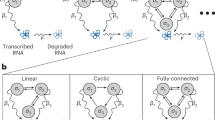
The raw reads are converted into k-mer frequency vectors using the k-mers in the reference transcriptome (1). This table is then transformed into polynomial representations to enable homomorphic operations (2). These polynomials are subsequently encrypted and used for secure computation by the server (3), where the secure polynomial multiplication computes the inner product between the k-mer vector of the reads and the reference sequences of the genes. Finally, the client downloads the encrypted results and decrypt them using their key. This allows secure extraction of the gene expression values from the computed ciphertexts. Created in BioRender. Gursoy, G. (2025) https://BioRender.com/w38p348.
With the growing privacy risks surrounding genome privacy, there has been an increasing need for cryptographic solutions to secure genomic data. A more accessible descriptions of these solutions were previously provided within the context of genome privacy7,8,9. Homomorphic encryption is a cryptographic technique that enables direct computations of encrypted data within the public cloud or any other shared server10,11,12,13. However, this technique has faced significant bottlenecks in its applicability, scalability, and performance, and is typically only suited for arithmetic tasks that involve addition and multiplication. Extending it to handle more complex algorithms can therefore be challenging. Additionally, both the storage size of encrypted data (i.e., ciphertext) and the associated computation times are several orders of magnitude greater than those for the original plaintexts. However, recent advances in algorithm design and computing power have enabled an increase in the use of homomorphic encryption in genomics for Genome-Wide Association Studies14,15,16,17, genotype imputation18,19,20, variant querying21,22, regression analysis for rare disease variants23, and inference using genetic variants in machine learning applications24. These methods have introduced significant algorithmic breakthroughs, laying the foundation for more feasible and effective privacy-preserving genomic analyses. However, they are focused on solely genomic data and cannot account for the intricacies of transcriptomics data, and working with genetic variants (e.g., SNPs in a VCF file) and cannot work with large and complex data types such as reads from NGS. As a result, there remain no privacy-preserving solutions for transcriptomics data analysis despite the privacy leakages in the data6,7,25,26.
Adapting established RNA-seq quantification algorithms such as kallisto27 and STAR28 to function using homomorphic encryption protocols presents significant challenges for gene expression quantification. These challenges primarily stem from the restrictions on the types of mathematical operations and the complexity of algorithms that homomorphic encryption can accommodate (for detailed explanations, please refer to Supplementary Methods 3.1). Therefore, significant algorithmic innovations are required in order to develop a secure RNA-seq processing tool. To address this need, we developed pQuant, a secure and scalable algorithm for privacy-preserving quantification of gene expression from both single and paired-end RNA-seq data across public and cloud servers. Our evaluations demonstrate that pQuant matches the accuracy of state-of-the-art (SOTA) non-secure algorithms like STAR28 and kallisto27 in gene expression quantification and subsequent differential gene expression analyses. Crucially, pQuant’s performance is unaffected by the number of reads in an RNA-seq dataset, and it supports parallel processing, which decouples its efficiency from the number of genes. Moreover, its parameter space is dataset-independent and depends solely on publicly available reference gene sequences. This combination of features makes pQuant scalable, thus suitable for large-scale gene expression studies.
Results
In this paper, we present pQuant, an RNA-seq processing algorithm optimized for homomorphic encryption. It enables secure and efficient quantification of gene expression using NGS reads from RNA-seq experiments. Our method uses a one-time calculation of the inner product between vectors that represent the sequences in the reads and a gene.
Similar to plaintext gene expression quantification methods, pQuant uses an indexing scheme for the reference transcriptome. The indexing represents the reference genome sequences of the genes in a vector of k-mer frequencies. The reads from the sequencer are converted into a k-mer vector following this indexing, encoded as polynomials to enable homomorphic computations, encrypted, and uploaded to a cloud server (Fig. 1). The server then performs an encrypted inner product between the indexed gene vector (also represented as polynomials) and encrypted reads vector to output an encrypted gene expression value for the gene. This is repeated for all genes (in parallel or serially) and encrypted gene expression values for all genes are downloaded locally for decryption (see Methods and Fig. 1). To reduce computational overhead, we also introduce the concept of k-mer entropy. This enables us to retain k-mers that are nearly unique to a single gene by removing k-mers that do not meet a certain entropy (H) threshold.
The details of pQuant can be found in Methods (see also Box). In short, the proposed pQuant algorithm comprises four main steps:
-
1.
Encoding of the reference transcriptome: Either the server (cloud provider) or the client (data owner) can encode the reference transcriptome. This is a one time computation that can be used by all clients. This step outputs polynomial representations of the reference transcriptome, where each polynomial contains the encoded k-mer counts of the genes.
-
2.
Encoding and encryption of reads by the client: The client generates a secret key, encodes the reads and encrypts the encoded reads using the secret key. This step outputs the ciphertexts, which are the encryptions that contains parts of the reads in polynomial representations. Note that reads are also converted into the same k-mer representations as reference transcriptome.
-
3.
Evaluation by the server: The server computes the inner products between the plaintext polynomial representations of the reference transcriptome and the encrypted polynomial representations of the reads using homomorphic encryption.
-
4.
Decryption by the client: The client downloads and decrypts the encrypted final ciphertexts with their secret key to reveal the raw gene expression values. Note that there is no key exchange involved in our algorithm.
pQuant can accurately quantify gene expression
We first compared the accuracy of pQuant with respect to two established, non-secure SOTA gene expression quantification algorithms: kallisto27 and STAR aligner28. A comparative approach is essential because the accuracy of gene expression quantification cannot be directly determined from the data. Therefore, benchmarking our algorithm against SOTA tools is crucial for validation. For this benchmarking, we used a paired-end poly-A RNA-Seq dataset from the K562 cell line (see Overview of Datasets in Methods) and quantified gene expression using pQuant, kallisto, and STAR. All raw values were normalized as log2-transformed transcripts per million (TPM) with a pseudocount of 1 (i.e. log2(TPM+1) before comparison (see RNA-Seq data processing and downstream analysis section in Methods for details).
Figure 2 a illustrates the correlation between the expression quantifications (log2(TPM+1)) by pQuant and those obtained using kallisto and STAR. The results indicate that the expression output of pQuant has a strong correlation with STAR (R2 = 0.95) and kallisto (R2 = 0.91) with low RMSE of 0.41 and 0.54, respectively. The small deviation observed is within the expected range as a direct comparison between STAR and kallisto yields an R2 of 0.89 with RMSE of 0.60. These results show that the quantification precision of pQuant algorithm aligns with that of other non-secure SOTA algorithms.
Next we assessed whether the pQuant algortihm has any effect on downstream analyses by focusing on differential gene expression. We used pQuant, kallisto, and STAR to quantify gene expression in two distinct datasets: one from a pancreas tissue sample with six replicates, and one from an esophagus tissue sample with seven replicates (see Overview of Datasets in Methods). Using the DESeq2 method29 implemented in PyDESeq230, we then performed differential gene expression analysis for these samples using the raw gene counts obtained from each method. That is, for each set of gene expression values, we calculated maximum a posteriori log2-fold change estimates for every gene between the two tissues. Our results indicate that estimates of log2-fold change calculated using the expression output of pQuant has a strong correlation with those calculated using the expression output of STAR (R2 = 0.93) and kallisto (R2 = 0.93) with low RMSE of 0.62 and 0.52, respectively (Fig. 2b). The small deviation observed is within the expected range as a direct comparison between STAR and kallisto yields an R2 of 0.93 with RMSE of 0.58. These results show that the use of homomorphic encrytion in gene expression quantification does not affect the log2-fold change estimates in differential gene expression analysis.
pQuant is efficient and scalable
We evaluated the performance of pQuant in terms of time, memory, and data storage requirements. pQuant is designed to independently calculate the gene expression for each gene and can run in parallel, enabling simultaneous computation across all genes if resources permit. Consequently, we assessed the runtime and memory requirements on a per-gene basis. As illustrated in Fig. 3a, pQuant completes its runtime in approximately 1.5 to 3 minutes depending on the length of the gene, maintaining this duration regardless of the number of reads in the RNA-seq data. Figure 3b shows that the peak memory usage per gene remains stable at about 477 MB, even as the number of reads increases.
a Runtime per gene with an increasing number of reads: Given that each gene can be calculated independently, we executed pQuant for all genes in the transcriptome and documented the distribution of runtime. The runtime remains consistent despite the increasing number of reads, indicating that pQuant’s time complexity is independent of read count. Please note that the center line represents the median, the bounds of the box indicate the interquartile range (IQR, 25th to 75th percentile), the whiskers extend to 1.5 times the IQR, and outliers are shown as individual points beyond this range. Each dot belongs to a gene in a gtf file, total number of dots (genes) is ~40,000 including both protein coding and non-coding genes (see Overview of Datasets in Methods). This figure is derived from a single RNA-seq sample. b Peak memory per gene with an increasing number of reads remains constant. c pQuant’s ciphertext files contain aggregated k-mer frequency information across all reads, resulting in a constant size across varying read counts. d Reference index size with an increasing number of genes: pQuant’s reference index size is significantly smaller than that of STAR, but larger than kallisto’s.
We also analyzed the storage demands for pQuant’s encoded and encrypted read files. Despite encryption, these files are relatively efficient in size, typically around 8GB, which is only about 30% of the size of a 50 million read FASTQ file and smaller than kallisto’s pseudoBAM files. Although pQuant read files are about twice as large as the typical RNA-seq BAM files produced by STAR, pQuant file sizes do not increase with the increasing number of reads. However, it is important to note that both kallisto pseudoBAM and STAR BAM files contain read-level information that might be useful for more downstream analyses. In contrast, pQuant ciphertext contains only aggregated k-mer frequency information rather than read-level data (Fig. 3c). Furthermore, pQuant’s index is half the size of STAR’s but more than three times larger than kallisto’s (Fig. 3d). We also evaluated the time and memory requirements of local pre-processing steps, including encoding, encryption, and decryption (see Supplementary Table 1 and Supplementary Methods 3.10 for details). Additionally, we include a table that compares the end-to-end runtime of pQuant, STAR, and kallisto for an RNA-seq data of K562 cell lines (see Overview of Datasets in Methods and Supplementary Table 2).
We also report both the end-to-end runtime and the runtime requirements for each individual step performed on the user side. To assess this, we conducted an experiment quantifying gene expression values for all ~ 60,000 genes, processed in parallel batches of 120 genes (Fig. 4a). Our results show that an RNA-seq sample containing up to 80 × 107 reads can be fully quantified in approximately 4 hours while maintaining privacy and security. Additionally, we demonstrate that the steps performed locally-encryption, encoding, and decryption-are relatively fast (Fig. 4b-d). The runtime is predominantly driven by the quantification step performed in the cloud (Fig. 4c).
End-to-end time cost analysis for increasing number of reads ranging from 10 × 107 to 80 × 107, with ~60, 000 genes and fixed k = 20 and H = 10−9. The evaluation step is computed in 500 parallel batches, and results are averaged. Additional experiments for encoding, encryption, and decryption are run 10 times to measure consistency. All error bars represent the standard deviation. a End-to-end time cost, where total time is broken into four stages: encoding, encryption, evaluation (500 batches), and decryption. b User’s local encoding and encryption times remain consistently constant. c The mean of evaluation times shows slight variations but generally remains stable. d Decryption time is stable across all experiments, with standard deviation of approximately one second, which is not visible in the graph.
Lastly, we evaluated our tool’s performance with long-read data by measuring runtime across increasing read lengths, ranging from 100 bp to 10,000 bp (by simulating them). As expected, we observed that read length does not impact the runtime for reference indexing or server-side computations (Supplementary Fig. 4a,c). Encoding and encryption times initially increase with longer reads but then slightly decrease at larger read lengths due to the efficiency of k-mer pruning, which becomes more effective as additional k-mers are incorporated into the reads (Supplementary Fig. 4b). Decryption time remains constant, as it is determined by the number of gene expression values, which is only dependent on the number of genes and independent of both read length and the number of reads (Supplementary Fig. 4d).
Our findings confirm that server runtime and memory usage are unaffected by the number of reads, highlighting a key advantage of pQuant: the cost of server resources does not increase with increasing number of reads, making it highly efficient for processing large-scale transcriptomic data. All measurements were performed at the New York Genome Center’s High Performance Computing cluster using Intel Xeon Gold 6132 CPUs @ 2.60GHz.
pQuant is almost parameter-free
pQuant operates with two main parameters: k, which specifies the size of the k-mers, and H, which measures the entropy of the k-mers. These parameters are not dataset-specific but are derived from the characteristics of the human reference transcriptome sequences, allowing them to be universally applicable across all human RNA-seq datasets. In our study, we have set k = 20 and H = 10−9.
The parameter H determines the uniqueness of the k-mers within the reference transcriptome. Our findings indicate that a lower (or more stringent) H value enhances the algorithm’s efficiency by reducing the number of k-mers it needs to process, without compromising its accuracy (Supplementary Fig. 2 and 3). In summary, smaller H value (e.g, H = 10−9) allows the algorithm to perform faster, especially for large datasets, while maintaining output accuracy. Therefore, we recommend choosing a smaller value for H.
The choice of k, on the other hand, impacts both the accuracy and the computational efficiency of the algorithm. Our analysis shows that accuracy improves as k increases but stabilizes around k = 20 (Fig. 5a). Additionally, larger k values also lead to increases in both runtime and memory usage (Fig. 5b-c). Thus, we recommend k = 20 as it provides optimal accuracy while maintaining manageable computational demands.
Discussion
We introduce pQuant, a secure, and user-friendly gene expression quantification tool using homomorphic encryption. We envision pQuant as a valuable tool for data owners, consortia, hospitals, non-profit academic research institutions, and government health agencies, offering them a secure means to process their RNA-seq data obtained from thousands of individuals. We propose that our tool has the potential to be used for ultra-sensitive samples, delivering enhanced security measures without compromising accuracy and scalability. We demonstrate this by showing that pQuant’s accuracy is on par with SOTA non-secure counterparts and runtime and memory requirements are independent of the number of reads in a dataset. pQuant is also parallelized to run on multiple genes at a time.
While quantifying gene expression on local machines is resource efficient per sample, it can be demanding when data is collected from thousands of individuals in consortium settings, especially for data storage (about 5GB per sample per raw FASTQ for 10 million reads, also see Fig. 3c). Therefore, there is a need for cloud computing and other decentralized alternatives, which have the potential to further erode the privacy of research participants and patients or prohibit sharing altogether due to local, global, or institutional privacy policies. While there are mandates in place to ensure that cloud environments holding sensitive data are certified by the Federal Risk and Authorization Management Program, this solution is not always practical due to associated time, financial cost, and administrative overhead31. Moreover, with the introduction of the General Data Protection Regulation (GDPR) in Europe, the storage of genomic and related data in the cloud has become more stringent with the requirement of appropriate security measures in place such as encryption and access controls32,33. Starting in 2023, a growing number of states in the US (e.g., California, Connecticut, Colorado, Utah, and Virginia) also entered a new GDPR-like privacy era34. However, the landscape of privacy protection governed by laws and institutional policies remains volatile and uncertain, creating substantial hurdles for researchers, institutions, and the individuals whose data is at stake, including research participants and patients. We propose that if data must be encrypted on cloud servers, computations are still possible while the data remains encrypted.
Computations on encrypted data can be achieved through homomorphic encryption, a cryptographic method that allows computation on ciphertexts, producing an encrypted result that, when decrypted, matches the result of operations performed on the plaintext. Homomorphic encryption has several advantages over other cryptographic techniques used in genomics such as Secure Multiparty Computation (MPC)35 and Trusted Executive Environments (TEE)36,37. Computations with homomorphic encryption do not depend on communication between servers (such as MPC) and the security in homomorphic encryption is grounded in the hardness of specific mathematical problems while TEEs requires security at the hardware level. Consequently, homomorphic encryption is less vulnerable to privacy attacks and easily accessible for use in cloud settings.
The most direct approach to utilizing homomorphic encryption for gene expression quantification would be adopting widely used RNA-seq analysis algorithms to operate under homomorphic encryption protocols. We show that such direct adaption is not possible due to the limitations of homomorphic encryption (please see Suplementary Methods 3.1 for a detailed explanation). Thus, to leverage the privacy-preserving properties of homomorphic encryption in RNA-seq analysis, it is necessary to develop a quantification algorithm that is compatible with homomorphic encryption. There are two key considerations to develop such an algorithm. First, it should only employ simple mathematical operations, such as additions or multiplications. Second, it should be data-independent, meaning that any operations performed on encrypted data should be computed without any information of private data.
We developed pQuant with these considerations in mind. The current version enables gene-level expression quantification; however, to enhance computational efficiency, the intermediate files exclude read-level information. While read quality information could be integrated into the encoding and ciphertexts, this would increase storage requirements. However, we believe this will not be a significant issue as with the advancement of sequencing technologies, the read quality will only increase in the future. In the future, we plan to enhance pQuant's capabilities to include transcript-level expression quantification, single-cell RNA-seq processing, and splicing detection. An alternative direction could involve developing privacy-preserving techniques for detecting novel transcripts and isoforms. However, employing homomorphic encryption may not be the optimal choice, as such detection would necessitate enumerating all possible exon combinations for a given gene within the encrypted domain-a process that is computationally prohibitive.
We also believe that our k-mer pruning approach might offer a key advantage in efficiency for the future design of plaintext pseudoalignment-based transcript discovery methods. That is, by eliminating redundant k-mers and using only unique k-mers during reference indexing, our approach reduces the overall memory usage and computational overhead.
We envision a future where managing sensitive clinical samples from thousands of patients is seamless, despite the immense challenges posed by substantial data storage demands. Traditional reliance on cloud services for processing introduces critical security and privacy risks. Our framework overcomes these vulnerabilities by encoding and encrypting data at the point of sequencing. This approach eliminates the need for local storage of vast datasets, ensuring secure, efficient, and privacy-preserving cloud-based processing.
Methods
Overview of datasets
We obtained raw FASTQ files of poly-A paired-end sequencing for an isogenic replicate of the K562 cell line from the ENCODE project38, under biosample accession ENCBS087RNA. We additionally obtained all replicates associated with poly-A paired-end sequencing runs for two samples: (1) a pancreas tissue sample with six replicates under accession ENCSR629VMZ, and (2) an esophagus tissue sample with seven replicates under accession ENCSR102TQN.
A reference transcriptome was defined for all analyses using the reference human genome GRCh38 and basic gene annotations ("gencode.v44.basic.annotation.gtf”) from GENCODE version 4439. To define a final set of 39559 genes in the reference transcriptome, we filtered the GENCODE GTF file, retaining only genes with gene type: protein_coding, lncRNA, antisense, IG_C_gene, IG_D_gene, IG_J_gene, IG_LV_gene, IG_V_gene, IG_V_pseudogene, IG_J_pseudogene, IG_C_pseudogene, TR_C_gene, TR_D_gene, TR_J_gene, TR_V_gene, TR_V_pseudogene, or TR_J_pseudogene. We then used the resulting GTF to create a reference index file for pQuant, STAR, and kallisto using default parameters. No data were excluded from the analyses.
Overview of homomorphic encryption
Homomorphic Encryption (HE) enables computations to be performed on encrypted data. This property allows for the manipulation of sensitive data without compromising its security. However, its practical implementation is deemed to be limited due to significant computational overhead and slower performance compared to operations on plaintext data. Since the first introduction of the main concepts of fully HE (FHE)10, a number of different HE schemes have been proposed11,12,13,40,41,42. Each of these schemes is tailored to specific functionalities and message (i.e., data) spaces. In this work, we use Brakerski/Fan-Vercauteren (BFV) scheme40,41, which supports bounded integer message space and arithmetic operations between ciphertext and plaintext. This choice equips us to conduct addition and multiplication on encrypted integers. Working in integer space is advantageous when dealing with NGS data, which are typically represented as counts.
The security of BFV scheme is based on the hardness of Ring Learning with Error (RLWE) problem43. This problem is considered hard based on the difficulty of solving polynomial equations when the coefficients are perturbed by small errors. Specifically, in RLWE, one deals with polynomials over a ring (see Supplementary Method for explanation of polynomials over a ring), and the challenge arises from trying to find the original polynomials given only noisy versions of their product. The “error” component makes it challenging to reverse the process and retrieve the original information without the correct key. This hardness assumption is crucial for ensuring the security of systems based on RLWE, as it implies that an adversary cannot feasibly decrypt a message without the secret key, even with substantial computational resources. Note that the RLWE problem is considered quantum-safe. This means that it is believed to be secure against attacks by quantum computers. Building on the RLWE problem framework, in BFV, all components of the system, including messages, keys, and ciphertexts, are structured as polynomials.
Since in BFV, both plaintext and ciphertext are expressed as polynomials, we first define what a plaintext and ciphertext modulus are. The plaintext modulus (p) refers to a prime number that defines the coefficient size of the plaintext polynomials. It specifies the range of values within which plaintext data can be securely stored as ciphertext. The choice of the plaintext modulus affects the precision of arithmetic operations on the encrypted data. Meanwhile, the ciphertext modulus (q) sets an upper limit on the coefficient size of ciphertext polynomials. The ciphertext modulus directly impacts the security of the encryption scheme. Setting it too large might make the encryption vulnerable to attacks, while setting it too low can negatively impact computational efficiency. This is because q is related to the maximum capacity of error that the ciphertext can hold, and the error inside of a ciphertext increases after every operation, thus smaller q allows less number of operations (especially multiplications) between ciphertexts.
In the BFV scheme, the spaces for plaintexts and ciphertexts are defined by polynomial rings based on a given ring dimension n (which must be a power of 2) and a ciphertext modulus q. Specifically, the plaintext space is represented as \({R}_{p}={\mathbb{Z}}[X]/({X}^{n}+1,p)\), and the ciphertext space as \({R}_{q}={\mathbb{Z}}[X]/({X}^{n}+1,q)\). In these expressions, Rp and Rq are composed of polynomials of degree up to n − 1, with coefficients in the sets of integers modulo p for plaintexts and modulo q for ciphertexts, respectively. Please see Supplementary Methods 3.4 for more details.
In this work, we set the ring dimension n to 8192, the plaintext modulus p to 536, 903, 681, and the ciphertext modulus q as a product of two 60-bit primes. The choice of n means that each polynomial contains 8192 coefficients, allowing each ciphertext to store up to 8192 elements. As computations on plaintexts are performed modulo p, the computation results will match exact computation as long as the final value do not exceed approximately 536 × 106. The choice of n and q is informed by security analysis44,45 to ensure 128-bit security level, i.e., best-known attack would require 2128 operations. Moreover, q is selected not only to support one level of multiplication depth on a ciphertext, but also to enable efficient polynomial operations using RNS-variant of BFV scheme46.
Note that, in HE, there are several public libraries facilitating the implementation of specific schemes, including the BFV scheme used in this work. From the libraries listed in the HE standard guidelines45, we used the openFHE library (version 1.1.2)47 for its inclusion of optimized algorithms for the BFV scheme. openFHE is one of the few libraries actively updated to incorporate the latest research developments.
pQuant algorithm
pQuant estimates gene expression from RNA-seq reads through a process of k-mer matching. We developed a k-mer matching algorithm that aims to be both accurate and efficient. In this method, both genes and reads are represented by the number of k-mers that their sequences contain, where k is a pre-set length. Instead of directly aligning reads to genes, pQuant calculates the total number of each k-mer of the the reads present in a gene. This method depends on selecting a k value sufficiently large to ensure the uniqueness of each k-mer sequence (at least unique enough when sufficient number of k-mers from the same read is searched), thus facilitating the determination of whether a read originates from a particular gene. The aggregate count of all reads mapped to a gene provides an estimate of the raw expression level of that gene. Below we outline the steps of our algorithm and detail the innovations that allow for its computation using HE where possible.
pQuant is composed of multiple steps: (a) Reference indexing, which is a one time operation that can be done publicly as it only uses the reference sequences of the genes. Indexed reference gene sequences are then encoded in polynomials. (b) Encoding and encrypting the reads, which are one time operations performed locally after obtaining the reads. This requires using the k-mers in the indexes reference to convert the reads in to k-mer representations, encoding them in polynomials, and encrypting them before sending them to the cloud. The computational requirements in terms of runtime, memory, and files sizes are small (see Results). (c) The cloud environment then performs a homomorphic inner product operation between the indexed reference polynomial and encrypted polynomials obtained from the reads to output an encrypted vector containing the raw number of reads mapping to each gene. (d) The client downloads the encrypted output, decrypt it locally, and obtains the results. Please see Fig. 1 for a visual depiction of these steps.
In addition, pQuant offers optional pre- and post-analysis summary statistics to assess data quality and results. Before encoding and encrypting reads, pQuant can generate basic metrics, such as total number of k-mers and reads meeting a quality threshold. After decryption, the tool can output the number of genes with TPM values above a defined threshold. These statistics allow for quality assessment of input data and results while preserving privacy. Note that common quality controls for sequence quality/library complexity, contamination detection, and adapter removal should all be done before encoding and encryption.
Reference indexing
Given that the reference transcriptome is publicly available, we conduct the indexing in plaintext. This one-time operation can be executed either on a cloud server or locally. After indexing, the generated k-mer table becomes accessible for use by any client. We utilize an indexing method to ascertain the number of of each k-mer within every gene in the reference transcriptome, focusing only the sequences of exons. This approach could be extended to gene bodies to enable processing of data types such as full-length RNA-seq. We also index the reverse complement of the exon sequences, which is necessary when dealing with paired-end reads. Please see Supplementary Methods 3.5 for details.
We start by identifying all k-mers within a gene’s sequence. Taking a gene with the sequence “AACTGCTGAACT” and setting k = 4 as an example, all unique k-mers extracted would be “AACT”, “ACTG”, “CTGC”, … , and “GAAC”. These k-mers are then counted for the number of times they occur in the gene, producing a vector g = (2, 1, 1, …, 1) with index (AACT, ACTG, CTGC …, GAAC), where each element of the vector denotes the total number of the k-mer of index in order. We repeat this process for all genes in the reference to obtain a k-mer by gene table, where each element is the frequency of a k-mer in a gene (Supplementary Fig. 1).
Let’s assume there are Ng genes in the reference transcriptome. We first generate a list of k-mers, denoted as K, which constitutes the ordered set of all k-mers identified within the reference transcriptome. Following this, we assemble occurrence vectors \({{{\bf{g}}}}^{(1)},{{{\bf{g}}}}^{(2)},\ldots,{{{\bf{g}}}}^{({N}_{g})}\), where each vector g(i) is associated with the number of k-mers for the ith gene, with all observed k-mers being cataloged in the list K. Ultimately, this procedure culminates in the formation of the k-mer table \({T}_{{{\rm{gene}}}}=\{{g}_{j}^{(i)}\}\) for 0 ≤ j < ∣K∣, and 1 ≤ i ≤ Ng, encompassing ∣K∣ rows and Ng columns. Here i and j represents the gene and k-mer, respectively (Supplementary Fig. 1). We also use a k-mer pruning approach using entropy of the k-mer to reduce computational cost. Please see Supplementary Methods 3.5 and Supplementary Algorithm 1 for more details.
Read pre-processing
Reads undergo pre-processing as soon as they are obtained from the sequencer in the FASTQ format. This entails creating a k-mer table based on the publicly available indexed reference transcriptome. For example, if the read sequence is “AACTGC” and the index set is (AACT, CTGC, …, GCTG) as in the Supplementary Fig. 1b, then we compute and output r1 = (1, 1, …, 0), indicating the number of times each k-mer of reference k-mer table in the read. That is, after Tgene is available, the client leverages this information to construct a k-mer table for the reads, termed Tread. Tread enumerates and records the number of occurrences of all k-mers across the reads for every k-mer in K. As a result, Tread is structured with ∣K∣ rows and a single column. This column signifies the cumulative sum of the occurrence vectors rm for all reads, represented as r as in Supplementary Fig. 1b.
Enabling homomorphic encryption
After reference indexing and read pre-processing, the vectors g(i) and rm represent the total number of occurrence of each k-mer in the genes and the reads, respectively. For each gene i and each k-mer j, the entry \({g}_{j}^{(i)}\), the jth element of vector g(i), indicates the number of occurrence of the jth k-mer in the ith gene. The vector rm similarly stores the number of occurrences of k-mers in the same order for mth read. Thus, when we count the number of occurrence of each k-mer in mth read to ith gene, we compute the inner product \(\langle {{{\bf{g}}}}^{(i)},{{{\bf{r}}}}_{m}\rangle=\mathop{\sum }_{j=1}^{| K| -1}{g}_{j}^{(i)}\cdot {r}_{m,j}\). Here, rm,j denotes the number of occurence of the jth k-mer in the mth read. The product \({g}_{j}^{(i)}\cdot {r}_{m,j}\) computes the contribution of the jth k-mer to the intersection of read and gene by multiplying the number of times this k-mer appears both in the gene and the read. Summing these products across all k-mers accumulates the total number of k-mer matches between the gene and the read. Therefore, the sum obtained from inner product represents the joint k-mer count between a specific gene and a read. Finally, the total raw expression value for a single ith gene is the sum of all inner products between the gene and each reads as expression\({}^{(i)}=\mathop{\sum }_{m=1}^{{N}_{r}}\langle {{{\bf{g}}}}^{(i)},{{{\bf{r}}}}_{m}\rangle .\)
Since the inner product is distributive over addition, this property can be utilized to enhance the efficiency of our computational process. Before computation, we aggregate the k-mer vectors from all reads to use a single vector \({{\bf{r}}}=\mathop{\sum }_{m=1}^{{N}_{r}}{{{\bf{r}}}}_{m}\), which represents the total number of occurrence of each k-mer across all reads (Supplementary Fig. 1b). Consequently, the raw expression value for ith gene can be computed as a inner product between a gene vector g(i) and the aggregated read vector r as follows.
To be able to keep the reads encrypted, we need to be able to execute this process with HE. This entails encoding Tgene and Tread as polynomials, encrypting Tread, and performing inner product in HE.
Encoding indexed reference transcriptome with polynomials
Since in BFV the message space is polynomial, we need to encode the Tgene in polynomials. We turn the g(m), which stores the k-mers of the genes into polynomials \({g}_{m}^{(i)}(X)\) for 1 ≤ i ≤ Ng and 0≤m < Nc. Nc = ⌈∣K∣/n⌉ is the number of required ciphertexts. Recall that n − 1 is the degree of the polynomial from the ring dimension described above. Each polynomial \({g}_{m}^{(i)}(X)\) is defined as
Here, \({g}_{m}^{(i)}=0\) if m≥∣K∣. This can be done in plaintext in the server or locally as reference transcriptome is publicly available information. This is a one time calculation whose results can be re-used by multiple clients.
Encoding the reads with polynomials and encrypting them
We first encode the read vector r, which has a length of ∣K∣, into Nc number of polynomials rm(X), where each polynomial rm(X) is defined as
Here, we define rm = 0 if m ≥ ∣K∣ for simplicity. The client then generates a set of ciphertexts ctxtm = Enc(rm(X)) for each m using their key. Please see Supplementary Methods 3.6 and Supplementary Algorithm 2 for details.
Inner product between a gene vector and reads vector
By definition, the sum of all multiplications of corresponding polynomials \({r}_{m}(X)\cdot {g}_{m}^{(i)}(X)\) contains the desired value 〈g(i), r〉 as its constant term modulo Xn + 1. Hence, after homomorphically computing ctxt\({}^{(i)}=\mathop{\sum }_{m=0}^{{N}_{c}-1}{g}_{m}^{(i)}(X)\cdot\) ctxtk for each i, the client can download the encrypted results and obtain the desired output by decrypting ctxt(i) for each i. Please see Supplementary Methods 3.9 for details of inner product in HE and see Supplementary Methods 3.7 and Supplementary Algorithm 3 for details of the computations on the server.
Overview of the pQuant algorithm
In short, the proposed pQuant algorithm comprises four main steps:
-
1.
Indexing and encoding of the reference transcriptome: Either server or client can encode the reference transcriptome. This is a one time computation that can be used for all clients. This step outputs polynomial representations \({g}_{m}^{(i)}(X)\) of the reference transcriptome, where each polynomial contains the encoded k-mer counts of the genes.
-
2.
Encoding and encryption of reads by the client: The client generates a secret key, encodes the reads and encrypts the encoded reads using the secret key. This step outputs the ciphertexts {ctxtm}, which are the encryptions that contains parts of the read vector r as polynomial representations. Optional summary statistics can be generated at this stage for quality control of input data.
-
3.
Evaluation by the server: Server computes the inner products between the plaintext polynomial representations \({g}_{m}^{(i)}(X)\) of the reference transcriptome and the encrypted read dataset {ctxt(i)} using HE. This computation involves summing up the products of corresponding polynomials \(\mathop{\sum }_{m=0}^{{N}_{c}-1}{r}_{m}(X)\cdot {g}_{m}^{(i)}(X)\) for each i.
-
4.
Decryption by the client: The client downloads and decrypts the encrypted final ciphertexts with their secret key to reveal the desired output to obtain the raw gene expression values. Post-decryption summary statistics are available to assess the quality of results. Please see Supplementary Methods 3.8 and Supplementary Algorithm 4 for details of the decryption.
Note that there is no key exchange involved in our algorithm. Also note that since client encrypts their own reads, we can use a single key. But the protocol is the same when we use public-private key pair.
RNA-Seq data processing and downstream analysis
Prior to quantification using pQuant, read pairs were first concatenated (see Supplementary Methods 3.5 for details). Raw gene expression vectors were then produced from all pairs of sequencing reads using pQuant, STAR (version 2.7.10b) with the argument --quantMode GeneCounts, and kallisto quant (version 0.44.0), with their respective reference index files. We ran pQuant with k = 20 and H = 10−9 for all quantifications, and ran STAR and kallisto using default parameters. Transcript-level counts from kallisto were collapsed to gene-level counts for all analyses, and rounded to integers prior to differential expression analysis.
Following quantification, the raw gene expression vectors from each method were normalized using a log2(TPM+1) transformation to facilitate comparisons across methods. For differential gene expression comparisons, raw gene expression vectors with unexpressed genes removed were used as input to PyDESeq2 version 0.3.330 (a python implementation of the DESeq2 method29) to generate maximum a posteriori estimates of log2-fold change for each gene.
Statistics and reproducibility
No data were excluded from the analyses.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Data availability
The K562 cell line dataset used in this study is publicly available in the ENCODE Portal under accession ENCBS087RNA. The pancreas tissue sample dataset with six replicates is available in the ENCODE Portal under accession ENCSR629VMZ. The esophagus tissue sample dataset with seven replicates is available in the ENCODE Portal under accession ENCSR102TQN.
Code availability
Implementation of the pQuant algorithm48 (with Snakemake version 7.30.1, Python version 3.11.2 and Pulp version 2.7.0) is available at https://github.com/g2lab/pQuant and Zenodo at https://doi.org/10.5281/zenodo.14852648.
References
Wang, Z., Gerstein, M. & Snyder, M. RNA-Seq: a revolutionary tool for transcriptomics. Nat. Rev. Genet. 10, 57–63 (2009).
Im, H. K., Gamazon, E. R., Nicolae, D. L. & Cox, N. J. On sharing quantitative trait GWAS results in an era of multiple-omics data and the limits of genomic privacy. Am. J. Hum. Genet. 90, 591–598 (2012).
Jacobs, K. B. et al. A new statistic and its power to infer membership in a genome-wide association study using genotype frequencies. Nat. Genet. 41, 1253–1257 (2009).
Homer, N. et al. Resolving individuals contributing trace amounts of DNA to highly complex mixtures using high-density SNP genotyping microarrays. PLoS Genet. 4, e1000167 (2008).
Sankararaman, S., Obozinski, G., Jordan, M. I. & Halperin, E. Genomic privacy and limits of individual detection in a pool. Nat. Genet. 41, 965–967 (2009).
Gürsoy, G. et al. Data sanitization to reduce private information leakage from functional genomics. Cell 183, 905–917.e16 (2020).
Gürsoy, G. et al. Functional genomics data: privacy risk assessment and technological mitigation. Nat. Rev. Genet. 23, 245–258 (2022).
Berger, B. & Cho, H. Emerging technologies towards enhancing privacy in genomic data sharing. Genome Biol. 20, 128 (2019).
Bonomi, L., Huang, Y. & Ohno-Machado, L. Privacy challenges and research opportunities for genomic data sharing. Nat. Genet. 52, 646–654 (2020).
Gentry, C. Fully homomorphic encryption using ideal lattices. In Proceedings of the 41st Annual ACM Symposium on Theory of Computing (STOC), pp 169–178 (2009).
Brakerski, Z., Gentry, C. & Vaikuntanathan, V. (Leveled) fully homomorphic encryption without bootstrapping. ACM Transactions on Computation Theory (TOCT) 6, 1–36 (2014).
Chillotti, I., Gama, N., Georgieva, M. & Izabachène, M. Faster Fully homomorphic encryption: bootstrapping in less than 0.1 seconds. In Advances in Cryptology–ASIACRYPT 2016: 22nd International Conference on the Theory and Application of Cryptology and Information Security, pp 3–33 (Springer Berlin Heidelberg, 2016).
Cheon, J. H., Kim, A., Kim, M. & Song, Y. Homomorphic encryption for arithmetic of approximate numbers. In Advances in cryptology–ASIACRYPT 2017: 23rd international conference on the theory and applications of cryptology and information security, pp 409–437 (Springer International Publishing, 2017).
Sim, J. J., Chan, F. M., Chen, S., Meng Tan, B. H. & Mi Aung, K. Achieving GWAS with homomorphic encryption. BMC Med. Genomics 13, 90 (2020).
Blatt, M., Gusev, A., Polyakov, Y., Rohloff, K. & Vaikuntanathan, V. Optimized homomorphic encryption solution for secure genome-wide association studies. BMC Med. Genomics 13, 83 (2020).
Kim, M., Song, Y., Li, B. & Micciancio, D. Semi-Parallel logistic regression for GWAS on encrypted data. BMC Med. Genomics 13, 99 (2020).
Blatt, M., Gusev, A., Polyakov, Y. & Goldwasser, S. Secure large-scale genome-wide association studies using homomorphic encryption. Proc. Natl Acad. Sci. USA 117, 11608–11613 (2020).
Sarkar, E. et al. Fast and scalable private genotype imputation using machine learning and partially homomorphic encryption. IEEE Access 9, 93097–93110 (2021).
Kim, M. et al. Ultrafast homomorphic encryption models enable secure outsourcing of genotype imputation. Cell Syst. 12, 1108–1120.e4 (2021).
Gürsoy, G., Chielle, E., Brannon, C. M., Maniatakos, M. & Gerstein, M. Privacy-preserving genotype imputation with fully homomorphic encryption. Cell Syst. 13, 173–182.e3 (2022).
Kim, M. & Lauter, K. Private genome analysis through homomorphic encryption. BMC Med. Inform. Decis. Mak. 15, S3 (2015).
Chen, L., Al Aziz, M. M., Mohammed, N. & Jiang, X. Secure large-scale genome data storage and query. Computer Methods Prog. Biomed. 165, 129–137 (2018).
Wang, S. et al. HEALER: homomorphic computation of ExAct Logistic rEgRession for secure rare disease variants analysis in GWAS. Bioinformatics 32, 211–218 (2016).
Hong, S., Park, J. H., Cho, W., Choe, H. & Cheon, J. H. Secure tumor classification by shallow neural network using homomorphic encryption. BMC Genomics 23, 284 (2022).
Harmanci, A. & Gerstein, M. Quantification of private information leakage from phenotype-genotype data: linking attacks. Nat. Methods 13, 251–256 (2016).
Schadt, E. E., Woo, S. & Hao, K. Bayesian method to predict individual SNP genotypes from gene expression data. Nat. Genet. 44, 603–608 (2012).
Bray, N. L., Pimentel, H., Melsted, P. & Pachter, L. Near-optimal probabilistic RNA-seq quantification. Nat. Biotechnol. 34, 525–527 (2016).
Dobin, A. et al. STAR: ultrafast universal RNA-seq aligner. Bioinformatics 29, 15–21 (2013).
Love, M. I., Huber, W. & Anders, S. Moderated estimation of fold change and dispersion for RNA-seq data with DESeq2. Genome Biol. 15, 550 (2014).
Muzellec, B., Teleńczuk, M., Cabeli, V. & Andreux, M. PyDESeq2: a python package for bulk RNA-seq differential expression analysis. Bioinformatics 39, btad547 (2023).
Taylor, L. FedRAMP: history and future direction. IEEE Cloud Comput. 1, 10–14 (2014).
Hansson, M. Striking a balance between personalised genetics and privacy protection from the perspective of GDPR. In: GDPR and Biobanking, 31–42 (Springer, 2021).
Zaeem, R. N. & Barber, K. S. The effect of the GDPR on privacy policies: recent progress and future promise. ACM Trans. Manag. Inf. Syst. 12, 2:1–2:20 (2020).
U.S. data privacy laws to enter new era in 2023∣reuters.https://www.reuters.com/legal/legalindustry/us-data-privacy-laws-enter-new-era-2023-2023-01-12/. Accessed 2025-02-27.
Cho, H., Wu, D. J. & Berger, B. Secure genome-wide association analysis using multiparty computation. Nat. Biotechnol. 36, 547–551 (2018).
Kockan, C. et al. Sketching algorithms for genomic data analysis and querying in a secure enclave. Nat. Methods 17, 295–301 (2020).
Dokmai, N. et al. Privacy-preserving genotype imputation in a trusted execution environment. Cell Syst. 12, 983–993.e7 (2021).
An integrated encyclopedia of DNA elements in the human genome∣Nature. https://www.nature.com/articles/nature11247. Accessed 29 May 2025.
Frankish, A. et al. GENCODE 2021. Nucleic Acids Res. 49, D916–D923 (2021).
Fan, J. & Vercauteren, F., Somewhat Practical Fully Homomorphic Encryption. IACR Cryptology ePrint Archive, 2012:144 (2012).
Brakerski, Z. Fully homomorphic encryption without modulus switching from classical GapSVP. In Annual cryptology conference pp. 868–886. (Springer Berlin Heidelberg, 2012).
Ducas, L. & Micciancio, D. FHEW: bootstrapping homomorphic encryption in less than a second. In Annual international conference on the theory and applications of cryptographic techniques. pp. 617–640 (Springer Berlin Heidelberg, 2015).
Lyubashevsky, V., Peikert, C. & Regev, O., On ideal lattices and learning with errors over rings. In Advances in Cryptology—EUROCRYPT 2010 1–23. Springer LNCS 6110 (Springer, 2010).
Albrecht, M. et al. Homomorphic Encryption Security Standard. HomomorphicEncryption.org (2018).
Bossuat, J.-P. et al. Security guidelines for implementing homomorphic encryption. Preprint, IACR ePrint 2024/463 (2024).
Halevi, S., Polyakov, Y. & Shoup, V. An improved RNS variant of the BFV homomorphic encryption scheme. In Topics in Cryptology–CT-RSA 2019: The Cryptographers' Track at the RSA Conference 2019 Proceedings, pp. 83–105 (Springer International Publishing, 2019).
Al Badawi, A. et al. OpenFHE: open-source fully homomorphic encryption library. In proceedings of the 10th workshop on encrypted computing & applied homomorphic cryptography, pp. 53–63 (2022).
Hong, S., Walker, C. R., Choi, Y. A. & Gursoy, G. Secure and scalable gene expression quantification with pQuant. GitHub repository (2025). https://github.com/g2lab/pQuant.
Acknowledgements
This study is funded by grants from the National Human Genome Research Institute (R56HG013319 and R00HG010909) to G.G., National Institute of General Medicine (R35GM147004) to G.G., and Warren Alpert Foundation to G.G.
Author information
Authors and Affiliations
Contributions
G.G. conceived and initiated the study. S.H. developed and implemented the methodology. C.R.W. assisted in the development of the methodological framework. S.H., C.R.W., and Y.A.C. processed and analyzed the data. G.G., S.H., and C.R.W. drafted the paper, and Y.A.C. participated in the result discussions. S.H., C.R.W., and Y.A.C. provided critical revisions.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Thomas Manke, who co-reviewed with Adrian Salatino, and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Hong, S., Walker, C.R., Choi, Y.A. et al. Secure and scalable gene expression quantification with pQuant. Nat Commun 16, 2380 (2025). https://doi.org/10.1038/s41467-025-57393-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-025-57393-6