Observed different impacts of potential tree restoration on local surface and air temperature

Li, Yitao; Li, Zhao-Liang; Wu, Hua; Liu, Xiangyang; Lian, Xu; Si, Menglin; Li, Jing; Zhou, Chenghu; Tang, Ronglin; Duan, Sibo; Zhao, Wei; Leng, Pei; Song, Xiaoning; Shi, Qian; Zhao, Enyu; Gao, Caixia

doi:10.1038/s41467-025-57606-y

Download PDF

Article
Open access
Published: 08 March 2025

Observed different impacts of potential tree restoration on local surface and air temperature

Nature Communications volume 16, Article number: 2335 (2025) Cite this article

6119 Accesses
9 Altmetric
Metrics details

Subjects

Abstract

Tree restoration can cool or warm the local climate through biophysical processes. However, the magnitude of these effects remains unconstrained at large scales, as most previous observational studies rely on land surface temperature (Ts) rather than the more policy-relevant air temperature (Ta). Using satellite observations, we show that Ta responds to tree cover change at only 15–30% of the magnitude observed in Ts. This difference is supported by independent evidence from site observations, and can be attributed to the reduced aerodynamic resistance and the resultant flatter near-surface temperature profiles in forests compared to non-forests. At mid- or high-latitudes, the maximum seasonal biophysical Ta warming or cooling only accounts for approximately 10% of the equivalent climate effect of carbon sequestration in terms of magnitude, whereas the biophysical Ts effect can reach 40%. These findings highlight the importance of selecting the appropriate temperature metric in different applications to avoid exaggerating or underestimating the biophysical impacts of forestation.

Asymmetric impacts of forest gain and loss on tropical land surface temperature

Article 01 May 2024

Atmospheric chemistry enhances the climate mitigation potential of tree restoration

Article Open access 13 May 2025

Asymmetric influence of forest cover gain and loss on land surface temperature

Article 03 August 2023

Introduction

In the past decade, the significance of terrestrial ecosystems has gained increasing recognition in high-level climate policies and pledges aimed at combating global climate change^1,2. A majority of these commitments focus on forest ecosystems^3,4, as global forested areas currently store over 800 petagrams (Pg) of carbon and can absorb ~13 Pg of CO₂ from the atmosphere annually^5,6. Global efforts to reduce the greenhouse effect through forest restoration, known as the biochemical (bchem) feedback of forests, are essential to mitigate global warming^7,8. Meanwhile, forests present several biophysical (bph) characteristics, such as lower albedo and greater roughness length, resulting in the local cooling or warming effect compared to their neighboring openlands^9,10,11. The sign and magnitude of the local biophysical temperature effects can vary considerably based on spatial location and background climate, and are typically characterized by a shift from cooling effects in the tropics to warming effects in cold regions^12,13. Forest changes also affect the temperature of spatially nearby regions through advective transport, and even global temperature via altering the large-scale circulation patterns¹⁴. The magnitude of this nonlocal effect depends on the area extent and the geolocation of the changes^15,16. Forestation is advocated as an effective solution to achieve the carbon neutrality goal by 2050, and its biophysical feedback can positively or negatively contribute to carbon-related global climate mitigation (the biochemical effect)^17,18.

Currently, forestation practices are predominantly concentrated in limited and specific regions^19,20. Given that CO₂ is well-mixed in the atmosphere, the biochemical feedback on temperature becomes less important when focusing on the climate effects of forestation at regional scales²¹. In contrast, the biophysical effects of forestation can directly induce local cooling or warming, substantially mitigating or exacerbating climate change^22,23. The mapping of maximum local climate effect through potential forestation practices is informative for policymakers to develop better regional adaptation strategies.

However, existing assessments of large-scale vegetation–climate feedback are subject to various sources of uncertainty. Numerous model-based studies have evaluated the biophysical effects of forest changes under various scenarios over the last two decades^24,25. Such assessments are dependent on the model representation of surface processes and are biased by the low resolution of simulations^26,27. High-resolution remote sensing (RS) data provide an avenue for evaluating the potential biophysical effects of forest changes, through a comparison between spatially adjacent forest and non-forest pixels. Nonetheless, for most RS-based studies, the temperature metric is land surface temperature (Ts)^{12,28,29,30,31,32,33,34}, which is a crucial parameter involved in surface energy or water balance processes but has limitations in characterizing the climate effects of forest change. According to the report of the Intergovernmental Panel on Climate Change (IPCC), the indicator used to describe global land warming and frame climate change mitigation targets is land surface air temperature (Ta) rather than Ts³⁵. Despite the strong correlation between Ts and Ta³⁶, the Ts effect of forest change may significantly differ from the Ta effect³⁷. Ts-based assessments are useful for model refinement or informing the sign of Ta effect, but the values cannot be directly considered in climate treaties or policies. Although a few studies have explored the different responses of these two temperatures in the context of forest change^38,39,40, their results may be affected by the uncertainties in numerical models or the sparse distribution of paired forest and non-forest sites. Consequently, it is still unclear whether the biophysical effects of forest change on Ts are comparable with those on Ta at large scales, posing challenges to the direct application of RS-based assessments for policymaking purposes and model result constraints.

This study aims to provide solid observational constraints for the biophysical sensitivity of different temperature metrics to tree cover change and evaluate the impact of potential tree restoration on the local climate. We first estimate the local biophysical Ts and Ta sensitivity to the full tree cover restoration (denoted as ${{{{\rm{\delta }}}}{{{\rm{Ts}}}}}^{{{{\rm{bph}}}}}$ and ${{{{\rm{\delta }}}}{{{\rm{Ta}}}}}^{{{{\rm{bph}}}}}$) at the 0.25° scale, based on the space-for-time analogy (Supplementary Fig. 1)^12,41,42. Notably, the evaluated Ts indicates the radiometric temperature of the land surface, and Ta indicates the air temperature at 2 m above the land surface (Supplementary Fig. 2). The land surface here refers to the interface layer between different land components and the atmosphere (e.g., vegetation canopy)⁴³. We revisit previous evaluations of the climate effects of forestation by comparing ${{{{\rm{\delta }}}}{{{\rm{Ts}}}}}^{{{{\rm{bph}}}}}$ and ${{{{\rm{\delta }}}}{{{\rm{Ta}}}}}^{{{{\rm{bph}}}}}$, and provide a comparative assessment of the sensitivities across latitudinal, seasonal, and diurnal dimensions. Furthermore, we use the FLUXNET2015 dataset⁴⁴ and two gridded temperature datasets to validate the differences between two sensitivities and elucidate the underlying biophysical mechanisms. Finally, we translate the biophysical temperature sensitivities to equivalent CO₂ metrics²², and compare them with the biochemical effects driven by the potential biomass increases, thereby informing the overall climate effects of forest-based climate strategies.

Results

Biophysical temperature sensitivities to tree cover gain

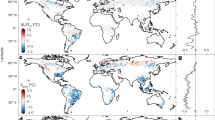
The RS-based biophysical sensitivities of annual mean Ts and Ta show similar spatial patterns in terms of sign (Fig. 1a, b). Both ${{{{\rm{\delta }}}}{{{\rm{Ts}}}}}^{{{{\rm{bph}}}}}$ and ${{{{\rm{\delta }}}}{{{\rm{Ta}}}}}^{{{{\rm{bph}}}}}$ exhibit positive values in northern high latitudes and negative values in other regions, delineated at around 50°N (Fig. 1c). This spatial distribution reflects a shift from non-radiative cooling in warm regions to radiative warming in cold regions^12,30. The estimated ${{{{\rm{\delta }}}}{{{\rm{Ts}}}}}^{{{{\rm{bph}}}}}$ aligns well with a previous study of the potential Ts effect of forestation based on the unmixing method⁴⁵, suggesting the robustness to different analytical approaches (Supplementary Fig. 3). In terms of magnitude, ${{{{\rm{\delta }}}}{{{\rm{Ta}}}}}^{{{{\rm{bph}}}}}$ demonstrates much lower absolute values compared to ${{{{\rm{\delta }}}}{{{\rm{Ts}}}}}^{{{{\rm{bph}}}}}$ (−0.14 ± 0.40 K vs. −0.65 ± 1.22 K, global mean ± standard deviation), indicating that the local Ta effect of tree restoration is ~22% of the Ts effect. The attenuated ${{{{\rm{\delta }}}}{{{\rm{Ta}}}}}^{{{{\rm{bph}}}}}$ relative to ${{{{\rm{\delta }}}}{{{\rm{Ts}}}}}^{{{{\rm{bph}}}}}$ can be observed across all latitudinal bands. At northern high latitudes, the Ta-based warming induced by tree cover change accounts for 32% of the Ts-based warming (0.17 vs. 0.53 K) (Fig. 1d). The ratio of Ta-based cooling to Ts-based cooling is about 40% (−0.32 vs. −0.80 K) at northern mid-latitudes, 17% (−0.24 vs. −1.41 K) at tropics, and 23% (−0.26 vs. −1.12 K) at southern mid-latitude (Fig. 1e–g). These quantitative results are robust to the choice of input tree cover data (Supplementary Fig. 4).

**Fig. 1: Annual mean temperature sensitivity to the full tree cover restoration.**

The monthly results further show similar seasonal variation patterns of ${{{{\rm{\delta }}}}{{{\rm{Ta}}}}}^{{{{\rm{bph}}}}}$ and ${{{{\rm{\delta }}}}{{{\rm{Ts}}}}}^{{{{\rm{bph}}}}}$, with differing intensities of cooling or warming (Supplementary Fig. 5). In boreal regions, where forest gains predominantly lead to cold season warming effects, the positive monthly ${{{{\rm{\delta }}}}{{{\rm{Ta}}}}}^{{{{\rm{bph}}}}}$ are considerably lower than ${{{{\rm{\delta }}}}{{{\rm{Ts}}}}}^{{{{\rm{bph}}}}}$. The ratios of ${{{{\rm{\delta }}}}{{{\rm{Ta}}}}}^{{{{\rm{bph}}}}}$ to ${{{{\rm{\delta }}}}{{{\rm{Ts}}}}}^{{{{\rm{bph}}}}}$ in these regions range from 21% to 30%. Conversely, at mid-latitudes, where forestation typically induces a strong growing season cooling effect, ~18% to 33% of the Ts-based cooling can translate into Ta-based cooling. In tropical regions, where forestation results in cooling throughout the year, the negative ${{{{\rm{\delta }}}}{{{\rm{Ta}}}}}^{{{{\rm{bph}}}}}$ accounts for about 15% of ${{{{\rm{\delta }}}}{{{\rm{Ts}}}}}^{{{{\rm{bph}}}}}$. These results highlight a consistent pattern in the response of two temperature metrics to forest change, albeit with varying magnitudes.

Previous studies have documented the diurnal asymmetry in the Ts effect of forestation, characterized by cooling at the daytime and warming at the nighttime^12,46. Our investigation into responses of daily maximum and minimum temperatures to tree cover gain reveals that both the daytime and nighttime Ta effects (${{{\rm{\delta }}}}{{{{\rm{Ta}}}}}_{\max }^{{{{\rm{bph}}}}}$ and ${{{\rm{\delta }}}}{{{{\rm{Ta}}}}}_{\min }^{{{{\rm{bph}}}}}$) are less pronounced compared to the corresponding Ts effects (${{{\rm{\delta }}}}{{{{\rm{Ts}}}}}_{\max }^{{{{\rm{bph}}}}}$ and ${{{\rm{\delta }}}}{{{{\rm{Ts}}}}}_{\min }^{{{{\rm{bph}}}}}$) (Supplementary Figs. 6 and 7). Globally, the mean ${{{\rm{\delta }}}}{{{{\rm{Ta}}}}}_{\max }^{{{{\rm{bph}}}}}$ is ~18% of the mean ${{{\rm{\delta }}}}{{{{\rm{Ts}}}}}_{\max }^{{{{\rm{bph}}}}}$ (−0.41 K vs. −2.24 K), whereas the mean ${{{\rm{\delta }}}}{{{{\rm{Ta}}}}}_{\min }^{{{{\rm{bph}}}}}$ accounts for about 15% of the mean ${{{\rm{\delta }}}}{{{{\rm{Ts}}}}}_{\min }^{{{{\rm{bph}}}}}$ (0.14 K vs. 0.94 K). Across most latitudinal zones, the extent of maximum and minimum Ta sensitivity is notably smaller than that of Ts sensitivity. An exception is observed in tropical nighttime, where the average ${{{\rm{\delta }}}}{{{{\rm{Ta}}}}}_{\min }^{{{{\rm{bph}}}}}$ and ${{{\rm{\delta }}}}{{{{\rm{Ts}}}}}_{\min }^{{{{\rm{bph}}}}}$ exhibit opposite signs (−0.04 K vs. 0.13 K) with small absolute values. Overall, we can conclude that roughly 15–30% of the previously observed Ts effects of forest change can translate into climate signals, a proportion that is notably lower than the nearly 50% conversion rate estimated by earth system models³⁹.

Validation of the magnitude of Ta sensitivity

Given that the Ta data used for assessment are empirically derived from satellite Ts, rather than direct observations, the accuracy of ${{{{\rm{\delta }}}}{{{\rm{Ta}}}}}^{{{{\rm{bph}}}}}$ might be dampened by the potential misrepresentations of the Ta retrieval model. To ensure the robustness of our findings, especially the relative magnitude of Ta effects to Ts effects, we further validate the RS-based ${{{{\rm{\delta }}}}{{{\rm{Ts}}}}}^{{{{\rm{bph}}}}}$ and ${{{{\rm{\delta }}}}{{{\rm{Ta}}}}}^{{{{\rm{bph}}}}}$ against the temperature effects of forestation (${{{{\rm{\delta }}}}{{{\rm{Ts}}}}}^{{{{\rm{bph}}}}*}$ and ${{{{\rm{\delta }}}}{{{\rm{Ta}}}}}^{{{{\rm{bph}}}}*}$) inferred from the in situ observations and gridded temperature data. Here, ${{{{\rm{\delta }}}}{{{\rm{Ts}}}}}^{{{{\rm{bph}}}}*}$ and ${{{{\rm{\delta }}}}{{{\rm{Ta}}}}}^{{{{\rm{bph}}}}*}$ are estimated in different shortwave radiation (SW_d) bins to represent the relative changes with changing background radiation conditions (see “Methods” and Supplementary Fig. 8).

The results show that both ${{{{\rm{\delta }}}}{{{\rm{Ts}}}}}^{{{{\rm{bph}}}}}$ and ${{{{\rm{\delta }}}}{{{\rm{Ts}}}}}^{{{{\rm{bph}}}}*}$ are negatively correlated with SW_d, and the slope obtained from in situ observations matches that derived from RS data (−1.14 vs. −1.39). For the Ta sensitivity, the negative slope derived from in situ observations (−0.24) is also nearly identical to the RS-based results (−0.27) (Fig. 2a, b). The comparable slope values indicate that in situ observations can quantitatively reflect the decrease in temperature sensitivity with increasing radiation, as seen in the RS-based results. Meanwhile, the ratio of slopes indicates that the relative magnitudes of Ta effects to Ts effects are also comparable between the RS-based (19.4%) and in situ results (21.1%).

**Fig. 2: Validation of the monthly land surface temperature and air temperature sensitivities.**

Since daytime maximum temperatures measure human exposure to heat stress⁴⁷, we also validate our findings of maximum Ta and Ts sensitivities via in situ measurements (${{{\rm{\delta }}}}{{{{\rm{Ts}}}}}_{\max }^{{{{\rm{bph}}}}*}$ and ${{{\rm{\delta }}}}{{{{\rm{Ta}}}}}_{\max }^{{{{\rm{bph}}}}*}$, Fig. 2c, d). The slopes derived from in situ measurements are more pronounced than RS-based results, which may be due to the satellite overpass times (around 13:30, see “Methods”) not precisely coinciding with the occurrence of daily maximum temperatures. However, we show that the ratios of Ta sensitivity slopes to Ts sensitivity slopes are close in the RS-based (16.9%) and site-based (17.4%) results (Fig. 2c, d). This result suggests that site measurements corroborate the relative magnitude of the RS-based maximum temperature sensitivity. In addition, we confirm that the validation results are robust irrespective of the choice of gridded temperature data used to control for the impact of macroclimate background (Supplementary Fig. 9). We also perform similar analyses on the site-based minimum Ta and Ts sensitivities (${{{\rm{\delta }}}}{{{{\rm{Ts}}}}}_{\min }^{{{{\rm{bph}}}}*}$ and ${{{\rm{\delta }}}}{{{{\rm{Ta}}}}}_{\min }^{{{{\rm{bph}}}}*}$, Supplementary Fig. 10), which supports the lower Ta-based warming than Ts-based warming during the nighttime in the RS-based results. We note that the relationship between ${{{\rm{\delta }}}}{{{{\rm{Ta}}}}}_{\min }^{{{{\rm{bph}}}}*}$ and SW_d is not significant, which corresponds to the weak correlation between ${{{\rm{\delta }}}}{{{{\rm{Ta}}}}}_{\min }^{{{{\rm{bph}}}}}$ and SW_d in the RS-based results (r = −0.38). Overall, these results verify the magnitude of the Ta sensitivities derived from the RS data, providing a strong basis for further analysis.

Biophysical mechanisms of the diverse temperature responses

To elucidate the biophysical mechanisms underlying the smaller magnitude of ${{{{\rm{\delta }}}}{{{\rm{Ta}}}}}^{{{{\rm{bph}}}}}$ than ${{{{\rm{\delta }}}}{{{\rm{Ts}}}}}^{{{{\rm{bph}}}}}$, we also analyze the vertical profile of temperature from the land surface to 2 m height at both forests and non-forested openlands, using the FLUXNET2015 and gridded temperature datasets (see “Methods”). We first focus on winter observations at European sites, which represent high latitudes where forestation leads to dormant season warming. We verify that site observations used in our study can capture the pattern of weaker Ta-based warming than Ts-based warming of forestation (0.16 vs. 1.63 K, Fig. 3a). In such cold environments, the near-surface boundary layer is generally in a stable condition, meaning that the atmosphere tends to warm the land surface, resulting in the temperature inversion phenomenon (Ta >Ts)⁴⁸. The temperature profiles show that the attenuation of ${{{{\rm{\delta }}}}{{{\rm{Ta}}}}}^{{{{\rm{bph}}}}*}$ in openlands is driven by a more pronounced temperature inversion compared to forests, where Ts is almost identical to Ta (Fig. 3a). Further examination of biophysical property differences reveals that both the absolute values of sensible heat flux (H) and aerodynamic resistance (r_a) are greater in openlands than in forests (H: −13.6 vs. −3.4 W·m⁻²; r_a: 178.1 vs. 30.7 s·m⁻¹, Fig. 3b). This implies two key factors: first, higher heat flux transfer in openlands favors more pronounced temperature gradients; second, lower transfer efficiency (higher r_a) can lead to larger temperature gradients even with constant heat flux. These factors collectively result in more significant temperature gradients in openlands (Fig. 3a), thereby contributing to the reduced Ta sensitivity. The quantitative analysis further shows that the impact through r_a (${{{\rm{\delta }}}}{{{{\rm{T}}}}}^{{{{{\rm{r}}}}}_{{{{\rm{a}}}}}}$, 55%) slightly outweighs the impact through H (${{{\rm{\delta }}}}{{{{\rm{T}}}}}^{{{{\rm{H}}}}}$, 45%) (Fig. 3c).

**Fig. 3: Attribution of differences in temperature sensitivities.**

We also examine summer observations from North American and Australian sites to understand the mechanisms underlying the reduced Ta cooling in mid- and low-latitude regions. Our results confirm that observations from both regions are consistent with the result of the smaller magnitude of ${{{{\rm{\delta }}}}{{{\rm{Ta}}}}}^{{{{\rm{bph}}}}*}$ than that of ${{{{\rm{\delta }}}}{{{\rm{Ts}}}}}^{{{{\rm{bph}}}}*}$ (North America: −0.25 vs. −2.23 K, Australia: −1.13 vs. -3.28 K, Fig. 3d, g). In these warm regions, the land surface is warmer than the ambient air, and the near-surface atmosphere is unstable, characterized by an upward sensible heat flux. The diminished Ta-based cooling effect in forests is attributed to stronger temperature gradients in openlands than in forests (Fig. 3d, g). In terms of the biophysical properties, openlands exhibit higher r_a than forests (North America: 49.2 vs. 9.2 s·m⁻¹; Australia: 45.3 vs. 16.1 s·m⁻¹), whereas the sensible heat flux appears to be similar (Fig. 3e, h). The quantitative analysis also shows that the weaker air cooling is primarily due to forest-resultant decrease of r_a (North America: 82%; Australia: 78%, Fig. 3f, i). Thus, it can be concluded that larger r_a values in openland lead to more pronounced Ts and Ta gradients, resulting in attenuation of the Ta-based cooling effect. These findings confirm the crucial role of r_a in influencing the impacts of both Ts and Ta in response to land cover changes⁴⁹. We note that the contribution of H is greater in European winter than in North American or Australian summer. The possible reason is that H is more dominant in the turbulent flux exchange during winter (characterized by the higher Bowen ratio) than summer⁵⁰, thus contributing more to the temperature gradients between the land surface and the near-surface air, and further to the attenuation of the air temperature response.

Comparison of biophysical with biochemical effects based on two temperature metrics

Most assessments of the climate benefits related to forestation have concentrated on carbon sequestration (i.e., biochemical effects)^51,52. Here, the biomass carbon stock sensitivity to tree cover is estimated via space-for-time analogy and converted to CO₂ absorption equivalents (${{{{\rm{\delta }}}}{{{{\rm{CO}}}}}_{2}{{{\rm{e}}}}}^{{{{\rm{bchem}}}}}$) to represent the biochemical effect. We also convert the biophysical Ts and Ta sensitivities to the metric of equivalent CO₂ uptake (${{{{\rm{\delta }}}}{{{{\rm{CO}}}}}_{2}{{{\rm{e}}}}}^{{{{\rm{bph}}}},{{{\rm{Ts}}}}}$ and ${{{{\rm{\delta }}}}{{{{\rm{CO}}}}}_{2}{{{\rm{e}}}}}^{{{{\rm{bph}}}},{{{\rm{Ta}}}}}$, Supplementary Fig. 11). These allow the comparison of the local biophysical and biochemical climate effects and evaluation of the relative importance of the former^22,23.

The spatial map shows that ${{{{\rm{\delta }}}}{{{{\rm{CO}}}}}_{2}{{{\rm{e}}}}}^{{{{\rm{bchem}}}}}$ in tropical rainforest margins can exceed 600 t·ha^-1 (Fig. 4a), which is comparable to the previous estimation of tropical intact forest based on ecological research network observations⁵. This value is greater than ${{{{\rm{\delta }}}}{{{{\rm{CO}}}}}_{2}{{{\rm{e}}}}}^{{{{\rm{bchem}}}}}$ in temperate and boreal forests, suggesting the highest carbon benefit of restoring damaged or degraded tropical forests. Latitudinally, ${{{{\rm{\delta }}}}{{{{\rm{CO}}}}}_{2}{{{\rm{e}}}}}^{{{{\rm{bchem}}}}}$ at low latitudes is higher than that at mid- or high latitudes, with a global mean of 268.2 ± 37.8 t·ha⁻¹ (mean ± uncertainty) (Fig. 4b). In terms of the biophysical effect, ${{{{\rm{\delta }}}}{{{{\rm{CO}}}}}_{2}{{{\rm{e}}}}}^{{{{\rm{bph}}}},{{{\rm{Ts}}}}}$ (41.7 ± 9.3 t·ha⁻¹) provides a global average of 15.7% additional benefits to ${{{{\rm{\delta }}}}{{{{\rm{CO}}}}}_{2}{{{\rm{e}}}}}^{{{{\rm{bchem}}}}}$ (Fig. 4b). However, if the more relevant biophysical Ta effect is considered, the ratio of ${{{{\rm{\delta }}}}{{{{\rm{CO}}}}}_{2}{{{\rm{e}}}}}^{{{{\rm{bph}}}},{{{\rm{Ta}}}}}$ (9.3 ± 2.9 t·ha⁻¹) to ${{{{\rm{\delta }}}}{{{{\rm{CO}}}}}_{2}{{{\rm{e}}}}}^{{{{\rm{bchem}}}}}$ is only 3.5%.

**Fig. 4: Comparison of the biophysical (bph) and biochemical (bchem) effects of potential tree cover gain.**

We then focus on northern high latitudes, where tree restoration shows a biophysical warming effect. The resultant negative ${{{{\rm{\delta }}}}{{{{\rm{CO}}}}}_{2}{{{\rm{e}}}}}^{{{{\rm{bph}}}},{{{\rm{Ts}}}}}$ could offset 9.5% of the ${{{{\rm{\delta }}}}{{{{\rm{CO}}}}}_{2}{{{\rm{e}}}}}^{{{{\rm{bchem}}}}}$ annually (Fig. 4b). The high-latitude biophysical warming is more pronounced in the cold season and can reduce the biochemical climate effect by 42.4% in March (Fig. 4c). However, when ${{{{\rm{\delta }}}}{{{{\rm{CO}}}}}_{2}{{{\rm{e}}}}}^{{{{\rm{bph}}}},{{{\rm{Ta}}}}}$ is used as the indicator, the offset of biophysical to biochemical effects is only 3.3% at the annual scale, with the maximum monthly value of 10.6% (February) (Fig. 4b, c). In mid-latitudes, the seasonal ${{{{\rm{\delta }}}}{{{{\rm{CO}}}}}_{2}{{{\rm{e}}}}}^{{{{\rm{bph}}}},{{{\rm{Ts}}}}}$ can enhance ${{{{\rm{\delta }}}}{{{{\rm{CO}}}}}_{2}{{{\rm{e}}}}}^{{{{\rm{bchem}}}}}$ by up to 33.7% (northern hemisphere) and 40.5% (southern hemisphere) during summer. However, these seasonal ratios are only about 10% considering ${{{{\rm{\delta }}}}{{{{\rm{CO}}}}}_{2}{{{\rm{e}}}}}^{{{{\rm{bph}}}},{{{\rm{Ta}}}}}$ (Fig. 4d, f). In low latitudes, annual positive ${{{{\rm{\delta }}}}{{{{\rm{CO}}}}}_{2}{{{\rm{e}}}}}^{{{{\rm{bph}}}},{{{\rm{Ts}}}}}$ is equivalent to 25.5% of ${{{{\rm{\delta }}}}{{{{\rm{CO}}}}}_{2}{{{\rm{e}}}}}^{{{{\rm{bchem}}}}}$, while the ratio for ${{{{\rm{\delta }}}}{{{{\rm{CO}}}}}_{2}{{{\rm{e}}}}}^{{{{\rm{bph}}}},{{{\rm{Ta}}}}}$ is only 6.2%, with insignificant seasonal variations (Fig. 4b, e). These results suggest that the relative importance of biophysical effects largely depends on the evaluated temperature metric, and the role of biophysical effects in the overall climate effect (usually measured by Ta) may not be as important as estimated in previous Ts-based studies^22,23.

Discussion

Previous studies have demonstrated that in boreal regions, forests can warm local Ts because the tree canopy is darker than the snow background and absorbs more solar radiation; in tropical regions, forests show strong local Ts cooling, mainly due to the higher evapotranspiration rates than other vegetation or bare land; in temperate regions, the net Ts effect depends on the relative magnitude of these two processes^10,12,28,30. However, the Ta effects cannot be simply extrapolated from the Ts effect, as the vertical mixing or coupling between Ts and Ta is much stronger in “rougher” forests than in “smoother” openlands^{13,37,38,39,53}. Leveraging satellite observations, we start by analyzing the biophysical sensitivities of Ta and Ts to tree cover gain. We quantify that ~15–30% of the Ts response could be translated into the Ta response. The less substantial Ta response than the Ts response is validated and further elucidated through in situ measurements, related to the distinct aerodynamic characteristics of forest canopies. Our findings underscore the duality of local Ts and Ta effects induced by tree cover gain, providing a universal metric for translating previous Ts-based results into climate effects. Through the comparison of biophysical and biochemical effects, we find that using Ts as the indicator may overestimate the role of biophysical processes in the overall climate effect of forestation. The evaluation based on the more relevant Ta can present better policy guidance for prioritizing the location of forestation.

The following points should be noted when our results are interpreted. First, akin to prior observational studies, our assessment of biophysical effects does not account for nonlocal or teleconnected effects²⁵, which could be substantial under scenarios of extensive global tree restoration. For instance, widespread restoration might alter atmospheric circulation patterns⁵⁴ and hydrological processes⁵⁵ at large or mesoscale scales, thereby affecting the temperature of non-forested areas. The nonlocal effect of forestation can even exceed the local effects in model simulations¹⁵. Therefore, our estimation of climate benefits should be viewed as the local effect of tree restoration at specific locations. The complex nonlocal feedbacks are better quantified through model simulations, and our findings can serve as constraints for model-based evaluations to more accurately quantify higher-order feedbacks. Second, the estimated biophysical sensitivity of tree restoration is contingent upon current climate conditions, and the impact may evolve in the future. For example, the positive biophysical sensitivity in boreal regions might become negative as snow-induced radiative effects decrease in a warmer world; the impact of rising CO₂ levels could also have profound impacts on the climate consequences of forestation⁵⁶. Nonetheless, our observational assessment could be useful for selecting models that better present the biophysical properties of forests and based on which to investigate the climate effects of forestation in future scenarios. Caveats should also be noted for our comparison of biophysical and biochemical effects. Both evaluated biophysical and biochemical effects represent potential cumulative results. It may take a shorter period for biophysical processes (a single decade) to come into effect than biochemical processes, as the newly restored forests gradually absorb CO₂ and reach equilibrium after several decades. In addition, potential variations in soil carbon are ignored in the biochemical part. In contrast to increases in biomass, tree restoration could have positive and negative effects on soil carbon, depending on the climate background and the ecosystem type^57,58,59. At the global scale, forestation can increase soil organic carbon, but the value is highly uncertain⁶⁰. Neglecting the potential change in soil carbon may lead to a slight underestimation of the biochemical effect⁶¹. The evaluated change in biomass should be the main contributor to carbon sequestration⁶².

In the context of global climate change, Ts and Ta show comparable variation patterns and trend values³⁶. However, when assessing the temperature effects of afforestation or deforestation, the Ts-based values can be about five times higher than the Ta-based values. This significant difference in magnitude highlights that attention should be given to the evaluated temperature metrics and the application scenarios when interpreting the biophysical effects of land cover changes. For instance, Ts (i.e., canopy temperature) could be the more appropriate metric when considering the effects of biophysical processes on ecosystem metabolism of photosynthesis, respiration, and transpiration^37,63. Meanwhile, the more relevant Ta should be used in analyses related to regional climate adaptation of tree restoration. We highlight that this issue should be considered in future RS-based studies focusing on the thermal buffering effects of forests.

Although Ta-based biophysical effect represents only a small proportion of equivalent biochemical effect, its role in local climate modulation should not be overlooked in regional adaptation strategies. In particular, the diurnal and seasonal changes in biophysical temperature effects should be considered when formulating comprehensive forest-based policies. For instance, we observe maximum temperature cooling and minimum temperature warming effects of forests at high latitudes. This suggests that tree restoration in such cold regions may be a solution to reduce the risks or impacts of daytime warming on the ecosystem. Meanwhile, we show that tree restoration at mid-latitudes can generate considerable summer maximum Ta cooling, indicating the potential for reducing the impact of hot extremes. Particularly for those mid-latitude countries with ambitious tree restoration goals, tree restoration can offer local climate benefits of mitigating summer heat stress in populated areas.

The biophysical warming effects of boreal forests should be given specific attention in related mitigation policies, although our results of negative biophysical climate effects at high latitudes may not be as strong as previous findings^64,65. This is because those studies focus on the additional radiative forcing induced by the darker forest canopy but ignore the impact of turbulent fluxes. The overlooked non-radiative effects could partially offset the albedo effects, leading to the observed net warming in our results. From the perspective of the whole climate system, the non-radiative effects represent the redistribution of energy within the climate system and may lead to warming in downwind regions or at the higher boundary layer⁶⁶. Thus, our results concerning the biophysical effects should be treated as the reference for local climate adaptation rather than global climate mitigation. The fact that the mitigation potential of high-latitude forestation could be reduced or even offset by the albedo impacts should be considered by forest-related global policies. Moreover, tree restoration can have numerous ecological, hydrological, and economic impacts besides the assessed temperature effects. Restoration in inappropriate geolocations (e.g., tropical savannas) can have counterproductive consequences such as ecosystem degradation, biodiversity loss, and water availability reduction^{67,68,69,70,71}. These impacts should also be considered in the development of comprehensive forest-related strategies to avoid the misconception that “restoring trees is the panacea for the current crisis”.

Methods

Tree cover map

In this study, two tree canopy cover datasets derived from different sensors are used for the analysis, including the recently released GLOBMAP fractional tree cover map with a spatial resolution of 250 m⁷², and the Global Forest Change (GFC) tree cover map with a spatial resolution of 30 m⁷³. Considering the data availability, we use the tree cover maps of 2010 (TC₂₀₁₀) of both two products to calculate the biophysical temperature sensitivities to ensure robustness. Both TC₂₀₁₀ maps from GLOBMAP and GFC are preprocessed and spatially aggregated to the 1 km resolution for further analysis (Supplementary Fig. 12).

Satellite-based Ts and Ta

The thermal infrared sensors onboard satellites provide direct measurements of Ts. In forested land, Ts represents the mixture temperature of the tree canopy and the exposed soil at the observed angle. Here, the monthly mean Ts data of 2010 are generated by the daily four observations from Moderate Resolution Imaging Spectroradiometer (MODIS) onboard Terra and Aqua satellites (observed at 1:30, 10:30, 13:30, and 22:30). Specifically, the four instantaneous Ts observations (MOD11A1/MYD11A1) are first converted to the daily mean values using the weighted average method⁷⁴, and the daily values are then temporally aggregated to monthly mean values⁷⁵. The synthesized monthly Ts data are the all-sky average with the spatial resolution of 1 km, and show satisfactory accuracy compared to the in situ measurements (root mean square error of 1.6 K). The daily maximum and minimum Ts data are calculated from the mean values of MODIS observations (13:30 and 1:30) at the monthly scale.

The other temperature metric used for assessment is Ta, the air temperature at ~2 m above the interface layer between the land components and the atmosphere. Specifically, for forested areas, the reference plane is the canopy, whereas for openlands, the reference plane is approximately the ground (Supplementary Fig. 2). Here, we use a state-of-the-art spatiotemporal seamless Ta dataset to analyze the local climate effect of potential forestation^76,77. This dataset is derived from a statistical model that correlates Ta from about 100,000 weather station records with satellite Ts (observed at 13:30 and 1:30) and other auxiliary variables. It provides global 1 km daily maximum and minimum air temperature data, with accuracies of ~2 K and ~1.5 K, respectively. We first aggregate the daily data to the monthly scale. Then, the monthly mean Ta data are calculated by arithmetically averaging the monthly maximum and minimum Ta values. Satellite monthly mean Ta and FLUXNET monthly mean Ta show good agreement. The validation results for forest and non-forest sites show comparable accuracy (Supplementary Fig. 13).

Calculation of biophysical temperature sensitivity maps

The biophysical sensitivity in this study is defined as the potential local temperature change when tree cover increases from 0 to 100%. A positive (or negative) sensitivity value at a given location indicates a local warming (or cooling) effect due to full restoration. This sensitivity is estimated using the space-for-time method^12,53, which assumes that the spatial variability of Ts or Ta within a designated area reflects land surface property differences, given that pixels within this area share the same macroclimate. Specifically, for each 0.25° × 0.25° grid cell²³, we filter out pixels with more than 1% water body coverage or less than 10% tree cover according to the forest definition by the Food and Agricultural Organization⁷⁸. This process is to reduce the impact of non-forest land cover types on the estimation of temperature sensitivity. We also exclude pixels with elevation differences exceeding 100 m from the average elevation of the 0.25° grid to avoid the potential impact of altitude on temperature. The water coverage and elevation data are from Joint Research Center Global Surface Water Mapping Layers v1.4⁷⁹ and GMTED2010 datasets, respectively.

After the screening process, ${{{{\rm{\delta }}}}{{{\rm{Ts}}}}}^{{{{\rm{bph}}}}}$ and ${{{{\rm{\delta }}}}{{{\rm{Ta}}}}}^{{{{\rm{bph}}}}}$ can be estimated using a linear regression model between tree cover and corresponding temperature values for each 0.25° grid^13,80,81 by Eqs. (1) and (2):

$${{{\rm{Ts}}}}={{{{\rm{\delta }}}}{{{\rm{Ts}}}}}^{{{{\rm{bph}}}}}\times \,{{{\rm{T}}}}{{{{\rm{C}}}}}_{2010}+{{{{\rm{b}}}}}_{{{{\rm{s}}}}}$$

(1)

$${{{\rm{Ta}}}}={{{{\rm{\delta }}}}{{{\rm{Ta}}}}}^{{{{\rm{bph}}}}}\times \,{{{\rm{T}}}}{{{{\rm{C}}}}}_{2010}+{{{{\rm{b}}}}}_{{{{\rm{a}}}}}$$

(2)

where, ${{{{\rm{b}}}}}_{{{{\rm{s}}}}}$ and ${{{{\rm{b}}}}}_{{{{\rm{a}}}}}$ are the regression intercepts. To ensure the reliability of the results, biophysical sensitivity calculation is performed only when the total sample size of the linear regression model exceeds 90 (more than 10% of pixels within the 0.25° grid) and the difference between the highest and lowest tree cover is greater than 40%. ${{{{\rm{\delta }}}}{{{\rm{Ts}}}}}^{{{{\rm{bph}}}}}$ and ${{{{\rm{\delta }}}}{{{\rm{Ta}}}}}^{{{{\rm{bph}}}}}$ are calculated using monthly data from 2010, and the extreme 1% values at both ends are removed from each sensitivity map to exclude outliers. The annual sensitivity is then averaged from these monthly results. In addition to mean temperature, we also calculate sensitivities for maximum and minimum temperatures using the same method, thereby exploring the diurnal temperature effects of forestation in more detail. Notably, all the sensitivity results should be interpreted as the temperature consequences of restoration with native forest type, as the gridded tree cover data of existing species are used as inputs to the spatial regression model.

Validation of RS-based biophysical sensitivities

Previous model-based and site-based studies have shown that Ts and Ta exhibit distinctive responses to forestation or deforestation processes at various scales^38,39,40. Here, our RS-based quantitative analysis also shows that the Ta effect is considerably weaker than the Ts effect. However, it is important to note that the Ta data employed for calculating biophysical sensitivity are derived from a statistical model using satellite Ts observations as inputs, rather than from direct space-based measurements. This raises the possibility that the calculated ${{{{\rm{\delta }}}}{{{\rm{Ta}}}}}^{{{{\rm{bph}}}}}$ might be influenced more by uncertainties inherent in the Ta statistical model across different land cover types, rather than accurately reflecting the true Ta effect of tree cover change. Therefore, there is a need to corroborate the magnitude of ${{{{\rm{\delta }}}}{{{\rm{Ta}}}}}^{{{{\rm{bph}}}}}$ and the relative ratio of the two sensitivities using additional evidence.

The RS-based local temperature sensitivity can be validated through the differences in measurements between spatially adjacent paired forest and non-forest sites. However, the sparse spatial distribution of such paired sites is insufficient to support global-scale validation of biophysical sensitivity^34,82. Inspired by the methodology proposed in a previous study⁸³, we use comprehensive flux tower measurements with the requisite variables from the monthly FLUXNET2015 Tier 1 dataset (Supplementary Table 1), along with interpolated air temperature data from the Climatic Research Unit (CRU TS4.06) and Berkeley Earth Surface Temperatures (BEST)^84,85 to validate the results. The method is based on assumptions that interpolated air temperature data primarily reflect macroclimate conditions and is, therefore, less sensitive to land cover; while the in situ measurements reflect the both impacts of land cover and macroclimate climate. Compared with traditional paired analysis, this methodology enables us to analyze the effects of Ts and Ta due to land cover changes, leveraging spatially distant tower data or temporally asynchronous observations.

The specific process of validation is as follows (Supplementary Fig. 8). In situ data for Ta are measured above the vegetation canopy, whereas Ts is estimated using the longwave radiation measurements⁸⁶ by Eq. (3):

$${{{\rm{Ts}}}}={\left[\frac{{{{\rm{L}}}}{{{{\rm{W}}}}}_{{{{\rm{u}}}}}-\left(1-{{{\rm{\varepsilon }}}}\right){{{\rm{L}}}}{{{{\rm{W}}}}}_{{{{\rm{d}}}}}}{{{{\rm{\varepsilon }}}}{{{\rm{\sigma }}}}}\right]}^{\frac{1}{4}}$$

(3)

where, LW_u and LW_d represent upward and downward longwave radiation from the FLUXNET2015 dataset, respectively; σ denotes the Stephan–Boltzmann constant (5.67 × 10⁻⁸ W m⁻² K⁻⁴), and ε is emissivity, estimated based on an empirical relationship with albedo⁸⁷. For the gridded data, we first make corrections using the lapse rates to compensate for the elevation difference between the site and the corresponding grid. The lapse rate for the target grid is estimated by the regression slope of the gridded temperatures and elevations within the 5 × 5 window.

By deducting the corrected gridded temperature data, the in situ measurements can effectively represent the land cover impacts on local Ts and Ta, assuming that macroclimate affects both temperature metrics similarly. Since the forest data cannot be directly matched with the openland data, we bin both forest and openland data points using the SW_d interval of 10 w·m⁻². For each SW_d bin, we calculate the difference between mean values of forest and openland data points to represent the temperature effect of forestation (i.e., ${{{{\rm{\delta }}}}{{{\rm{Ts}}}}}^{{{{\rm{bph}}}}*}$ or ${{{{\rm{\delta }}}}{{{\rm{T}}}}{{{\rm{a}}}}}^{{{{\rm{bph}}}}*}$) under the specific radiation background using Eqs. (4) and (5):

$${{{{\rm{\delta }}}}{{{\rm{Ts}}}}}^{{{{\rm{bph}}}}*}=\overline{\left({{{{{\rm{Ts}}}}}_{{{{\rm{f}}}}}^{{{{\rm{site}}}}}-{{{{\rm{T}}}}}_{{{{\rm{f}}}}}^{{{{\rm{grid}}}}}}\right)}-\overline{\left({{{{{\rm{Ts}}}}}_{{{{\rm{o}}}}}^{{{{\rm{site}}}}}-{{{{\rm{T}}}}}_{{{{\rm{o}}}}}^{{{{\rm{grid}}}}}}\right)} \quad {if}\ {{SW}}_{d}\in (10k,10k+10)$$

(4)

$${{{{\rm{\delta }}}}{{{\rm{Ta}}}}}^{{{{\rm{bph}}}}*}=\overline{\left({{{{{\rm{Ta}}}}}_{{{{\rm{f}}}}}^{{{{\rm{site}}}}}-{{{{\rm{T}}}}}_{{{{\rm{f}}}}}^{{{{\rm{grid}}}}}}\right)}-\overline{\left({{{{{\rm{Ta}}}}}_{{{{\rm{o}}}}}^{{{{\rm{site}}}}}-{{{{\rm{T}}}}}_{{{{\rm{o}}}}}^{{{{\rm{grid}}}}}}\right)} \quad {if}\ {{SW}}_{d}\in (10k,10k+10)$$

(5)

Here, ${{{{\rm{Ts}}}}}_{{{{\rm{f}}}}}^{{{{\rm{site}}}}}$ and ${{{{\rm{Ta}}}}}_{{{{\rm{f}}}}}^{{{{\rm{site}}}}}$ refer to Ts and Ta measured at forest sites, respectively; ${{{{\rm{Ts}}}}}_{{{{\rm{o}}}}}^{{{{\rm{site}}}}}$ and ${{{{\rm{Ta}}}}}_{{{{\rm{o}}}}}^{{{{\rm{site}}}}}$ refer to Ts and Ta measured at openland sites; ${{{{\rm{T}}}}}_{{{{\rm{f}}}}}^{{{{\rm{grid}}}}}$ and ${{{{\rm{T}}}}}_{{{{\rm{o}}}}}^{{{{\rm{grid}}}}}$ refer to the corresponding gridded temperatures after the elevation correction; $k$ indicates counting of the SW_d bin. According to the metadata of the FLUXNET2015 dataset, forest sites include the following four IGBP land cover types: evergreen needleleaf forests, evergreen broadleaf forests, deciduous broadleaf forests, and mixed forests; openland sites are categorized as other non-forest vegetation types.

Then, the relationships between two temperature sensitivities and SW_d are explored using the weighted least squares (WLS) regression model, in which the samples are ${{{{\rm{\delta }}}}{{{\rm{Ts}}}}}^{{{{\rm{bph}}}}*}$ or ${{{{\rm{\delta }}}}{{{\rm{T}}}}{{{\rm{a}}}}}^{{{{\rm{bph}}}}*}$ of all SW_d bins and the sample weights are defined as the inverse of the standard error of ${{{{\rm{\delta }}}}{{{\rm{Ts}}}}}^{{{{\rm{bph}}}}*}$ or ${{{{\rm{\delta }}}}{{{\rm{T}}}}{{{\rm{a}}}}}^{{{{\rm{bph}}}}*}$. The derived relationships are then compared with those from RS-based results for validation. Here, the monthly ERA5-Land shortwave radiation data are used to build the relationships with RS-based sensitivities. We also compare and validate the maximum and minimum temperature sensitivities.

Analysis of near-surface temperature profiles

To further investigate the biophysical mechanism behind the varying magnitudes of ${{{{\rm{\delta }}}}{{{\rm{Ts}}}}}^{{{{\rm{bph}}}}}$ and ${{{{\rm{\delta }}}}{{{\rm{Ta}}}}}^{{{{\rm{bph}}}}}$, we estimate and compare the vertical evolution from Ts to Ta in forest and openland sites. This comparison analysis uses daily meteorological, turbulence, and radiation records from sites in North America, Europe, and Australia (Supplementary Table 1). Specifically, we focus on winter observations from European sites (or summer observations from North American or Australian sites) to examine the typical magnitude differences in air and land surface warming (or cooling) effects of forestation.

Here, we first normalize the Ta measurements to the theoretical values at the 2-meter above the vegetation canopy to exclude the potential impact of measurement heights on the results³⁸. This normalization process is based on the parametrization of aerodynamic resistance (r_a) using the Monin–Obukhov similarity theory⁸⁸. Specifically, the theoretical relationship between Ts (the extrapolated temperature value at the height of heat roughness length plus zero-plane displacement) and Ta (the measured temperature above the canopy at height z) can be expressed by Eqs. (6) and (7):

$${{{\rm{Ta}}}}\left({{{\rm{z}}}}\right)={{{\rm{Ts}}}}-\frac{{{{\rm{H}}}}{{{{\rm{r}}}}}_{{{{\rm{a}}}}}({{{\rm{z}}}})}{{{{\rm{\rho }}}}{{{{\rm{C}}}}}_{{{{\rm{p}}}}}}$$

(6)

$${{{{\rm{r}}}}}_{{{{\rm{a}}}}}\left({{{\rm{z}}}}\right)=\frac{1}{0.4{{{{\rm{u}}}}}^{*}}\left[{{\mathrm{ln}}}\left(\frac{{{{\rm{z}}}}-{{{\rm{d}}}}}{{{{{\rm{Z}}}}}_{{{{\rm{oh}}}}}}\right)-{{{{\rm{\psi }}}}}_{{{{\rm{h}}}}}\left(\frac{{{{\rm{z}}}}-{{{\rm{d}}}}}{{{{\rm{L}}}}}\right)\right]$$

(7)

where ρ is the air density, C_p is the specific heat of air at constant pressure, d is the zero‐plane displacement and is assumed to be 67% of the vegetation height⁸⁹, u* is the friction velocity, Z_oh is the heat roughness length, and Ψ_h indicates the stable correction for heat, which is the function of the Monin–Obukhov length (L)⁸⁸. Z_oh, the only unknown parameter required to solve the temperature profile, is determined under certain conditions³⁸: (1) H has the same sign as Ts–Ta; (2) the absolute value of H exceeds 20 w·m⁻²; (3) u* is greater than 0.01 m·s⁻¹; and (4) the atmospheric stability parameter ($\frac{{{{\rm{z}}}}-{{{\rm{d}}}}}{{{{\rm{L}}}}}$) falls between 1 and -2³⁸. Invalid roughness length values are then filled using the relationship between the logarithm of inferred Z_oh and the friction velocity^38,90.

With the Z_oh inferred for both forest and openland sites, Ta can be estimated by modifying z to 2 m above the vegetation canopy in Eq. (6). Then, the impact of potential afforestation on Ta and Ts can be derived by comparing the near-surface temperature profiles of forest and openland sites. Similar to the sensitivity validation approach, we exclude the impact of background climate using the corresponding gridded air temperature data to ensure the comparability of the measurements. Meanwhile, through the first-order expansion of the analytical expression for Ta, we can decompose the air temperature sensitivity into the contributions from two biophysical parameters (${{{\rm{\delta }}}}{{{{\rm{T}}}}}^{{{{\rm{H}}}}}$ and ${{{\rm{\delta }}}}{{{{\rm{T}}}}}^{{{{{\rm{r}}}}}_{{{{\rm{a}}}}}}$) using Eq. (8), given the known sensitivity at Z_oh + d (${{{{\rm{\delta }}}}{{{\rm{Ts}}}}}^{{{{\rm{bph}}}}*}$):

$${{{{\rm{\delta }}}}{{{\rm{T}}}}{{{\rm{a}}}}}^{{{{\rm{bph}}}}*}={{{{\rm{\delta }}}}{{{\rm{T}}}}{{{\rm{s}}}}}^{{{{\rm{bph}}}}*}+{{{\rm{\delta }}}}{{{{\rm{T}}}}}^{{{{\rm{H}}}}}+{{{\rm{\delta }}}}{{{{\rm{T}}}}}^{{{{{\rm{r}}}}}_{{{{\rm{a}}}}}}$$

(8)

Here, ${{{\rm{\delta }}}}{{{{\rm{T}}}}}^{{{{\rm{H}}}}}$ and ${{{\rm{\delta }}}}{{{{\rm{T}}}}}^{{{{{\rm{r}}}}}_{{{{\rm{a}}}}}}$ are calculated by the partial derivatives $\left(\frac{\partial {{{{\rm{T}}}}}_{{{{\rm{a}}}}}}{\partial {{{\rm{H}}}}}\right.$ and $\left.\frac{\partial {{{{\rm{T}}}}}_{{{{\rm{a}}}}}}{\partial {{{{\rm{r}}}}}_{{{{\rm{a}}}}}}\right)$ and the parameter difference between forest and openland (${{{\rm{\delta }}}}{{{\rm{H}}}}$ and ${{{\rm{\delta }}}}{{{{\rm{r}}}}}_{{{{\rm{a}}}}}$, defined as forest minus openland) using Eqs. (9) and (10):

$${{{\rm{\delta }}}}{{{{\rm{T}}}}}^{{{{\rm{H}}}}}=\frac{\partial {{{{\rm{T}}}}}{{{{\rm{a}}}}}}{\partial {{{\rm{H}}}}}{{{\rm{\delta }}}}{{{\rm{H}}}}$$

(9)

$${{{\rm{\delta }}}}{{{{\rm{T}}}}}^{{{{{\rm{r}}}}}_{{{{\rm{a}}}}}}=\frac{\partial {{{{\rm{T}}}}}{{{{\rm{a}}}}}}{\partial {{{{\rm{r}}}}}_{{{{\rm{a}}}}}}{{{\rm{\delta }}}}{{{{\rm{r}}}}}_{{{{\rm{a}}}}}$$

(10)

This decomposition process allows a quantitative evaluation of why the absolute Ta response to forestation is smaller than the Ts response. Specifically, if ${{{\rm{\delta }}}}{{{{\rm{T}}}}}^{{{{\rm{H}}}}}$ is dominant, it implies that the differing sensible fluxes for heating or cooling the near-surface atmosphere are responsible for the milder air temperature response; if ${{{\rm{\delta }}}}{{{{\rm{T}}}}}^{{{{{\rm{r}}}}}_{{{{\rm{a}}}}}}$ is more significant, it suggests that changes in heat convection efficiencies, leading to different steepness in the temperature profiles, contribute to the attenuation of the air temperature response.

Comparison of biophysical and biochemical effects

In addition to regulating the energy balance process, forestation can enhance the land carbon sink through vegetation photosynthesis, thereby generating negative biochemical feedback on the climate system⁹¹. To quantify this biochemical impact, we first estimate the biomass carbon density sensitivity to ideal restoration, using Global Aboveground and Belowground Biomass Carbon Density Maps of 2010 (in t·ha⁻¹)⁹², along with TC₂₀₁₀ and the “space-for-time” strategy. We convert the biomass carbon stock sensitivity to CO₂ absorption equivalents (i.e., ${{{{\rm{\delta }}}}{{{{\rm{CO}}}}}_{2}{{{\rm{e}}}}}^{{{{\rm{bchem}}}}}$) based on the molar mass ratio. Notably, ${{{{\rm{\delta }}}}{{{{\rm{CO}}}}}_{2}{{{\rm{e}}}}}^{{{{\rm{bchem}}}}}$ provides a simple estimate of the ideal carbon stock in biomass under current climate and disturbance regimes for further comparison with the biophysical effect. The period for restored forests to reach such carbon potential, as well as the role of changing climate and soil carbon flux in this process are neglected.

The biophysical Ts and Ta sensitivities are also unified to the metric of CO₂ equivalents (${{{{\rm{\delta }}}}{{{{\rm{CO}}}}}_{2}{{{\rm{e}}}}}^{{{{\rm{bph}}}},{{{\rm{Ts}}}}}$ and ${{{{\rm{\delta }}}}{{{{\rm{CO}}}}}_{2}{{{\rm{e}}}}}^{{{{\rm{bph}}}},{{{\rm{Ta}}}}}$) using Eqs. (11) and (12), based on the transient climate response to cumulative emissions for both Ts (${{{{\rm{TCRE}}}}}^{{{{\rm{Ts}}}}}$) and Ta (${{{{\rm{TCRE}}}}}^{{{{\rm{Ta}}}}}$) derived from Coupled Model Intercomparison Project Phase 6 (CMIP6) simulations (Supplementary Fig. 11):

$${{{{\rm{\delta }}}}{{{{\rm{CO}}}}}_{2}{{{\rm{e}}}}}^{{{{\rm{bph}}}},{{{\rm{Ts}}}}}=\frac{{{{{\rm{\delta }}}}{{{\rm{Ts}}}}}^{{{{\rm{bph}}}}}}{{{{{\rm{TCRE}}}}}^{{{{\rm{Ts}}}}}}\times \frac{1}{{{{{\rm{A}}}}}_{{{{\rm{E}}}}}}$$

(11)

$${{{{\rm{\delta }}}}{{{{\rm{CO}}}}}_{2}{{{\rm{e}}}}}^{{{{\rm{bph}}}},{{{\rm{Ta}}}}}=\frac{{{{{\rm{\delta }}}}{{{\rm{Ta}}}}}^{{{{\rm{bph}}}}}}{{{{{\rm{TCRE}}}}}^{{{{\rm{Ta}}}}}}\times \frac{1}{{{{{\rm{A}}}}}_{{{{\rm{E}}}}}}$$

(12)

where, ${{{{\rm{A}}}}}_{{{{\rm{E}}}}}$ indicates the earth surface area (5.1 × 10⁸ km²). The gridded ${{{{\rm{TCRE}}}}}^{{{{\rm{Ts}}}}}$ and ${{{{\rm{TCRE}}}}}^{{{{\rm{Ta}}}}}$ are estimated following the previous study²², using 12 model simulations (ACCESS_ESM1-5, CanESM5-1, CMCC-ESM2, CNRM-ESM2-1, FIO-ESM-2-0, GISS-E2-1-H, INM-CM5-0, IPSL-CM6A-LR, MIROC6, MPI-ESM1-2-LR, MRI-ESM2-0 and NESM3) of the “1 percent per year increase in carbon dioxide” experiment (1pctCO2). In the calculation, we consider that 1 ppm of atmospheric CO₂ corresponds to 7.82 gigatonnes CO₂ and assume that the airborne fraction of the CO₂ flux is 43%¹³, as the 1pctCO2 experiment is based on the increase in CO₂ concentration, rather than the emission. Notably, ${{{{\rm{\delta }}}}{{{{\rm{CO}}}}}_{2}{{{\rm{e}}}}}^{{{{\rm{bph}}}},{{{\rm{Ts}}}}}$ and ${{{{\rm{\delta }}}}{{{{\rm{CO}}}}}_{2}{{{\rm{e}}}}}^{{{{\rm{bph}}}},{{{\rm{Ta}}}}}$ calculated by Eqs. (11) and (12) represent the CO₂ emission equivalents. We further convert their signs to align with the ${{{{\rm{\delta }}}}{{{{\rm{CO}}}}}_{2}{{{\rm{e}}}}}^{{{{\rm{bchem}}}}}$, which represent the CO₂ absorption equivalents. We compare the biophysical and biochemical effects based on the above metrics at both annual and monthly scales.

Data availability

All the data that support the findings of this study are openly available. GLOBMAP fractional tree cover can be downloaded from https://zenodo.org/records/10589730. GFC tree cover data are available at https://glad.umd.edu/dataset/global-2010-tree-cover-30-m. MODIS land surface temperature data are available at https://ladsweb.modaps.eosdis.nasa.gov/search/. Satellite-based air temperature data can be downloaded from https://iastate.figshare.com/collections/A_global_1_km_resolution_daily_near-surface_air_temperature_dataset_2003_2020_/6005185. The Joint Research Center Global Surface Water Mapping Layers are available at https://developers.google.com/earth-engine/datasets/catalog/JRC_GSW1_4_GlobalSurfaceWater. GMTED2010 Elevation data are available at https://developers.google.com/earth-engine/datasets/catalog/USGS_GMTED2010. CRU gridded temperature data can be downloaded at https://catalogue.ceda.ac.uk/uuid/e0b4e1e56c1c4460b796073a31366980. BEST gridded temperature data can be downloaded at https://berkeleyearth.org/data/. ERA5-Land reanalysis data are available at https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-land-monthly-means. Global Aboveground and Belowground Biomass Carbon Density Maps are available at https://developers.google.com/earth-engine/datasets/catalog/NASA_ORNL_biomass_carbon_density_v1. FLUXENET2015 dataset is available at https://fluxnet.org/. CMIP6 simulations can be downloaded from https://esgf-node.llnl.gov/search/cmip6/.

Code availability

The Python codes used to generate all the results are available at https://zenodo.org/records/14633331.

References

Seddon, N., Turner, B., Berry, P., Chausson, A. & Girardin, C. A. J. Grounding nature-based climate solutions in sound biodiversity science. Nat. Clim. Chang. 9, 84–87 (2019).
Article ADS Google Scholar
Griscom, B. W. et al. Natural climate solutions. Proc. Natl. Acad. Sci. USA 114, 11645–11650 (2017).
Article ADS CAS PubMed PubMed Central Google Scholar
Canadell, J. G. & Raupach, M. R. Managing forests for climate change mitigation. Science 320, 1456–1457 (2008).
Article ADS CAS PubMed MATH Google Scholar
Seymour, F. & Harris, N. L. Reducing tropical deforestation. Science 365, 756–757 (2019).
Article ADS CAS PubMed Google Scholar
Pan, Y. et al. The enduring world forest carbon sink. Nature 631, 563–569 (2024).
Article CAS PubMed MATH Google Scholar
Harris, N. L. et al. Global maps of twenty-first century forest carbon fluxes. Nat. Clim. Chang. 11, 234–240 (2021).
Article ADS MATH Google Scholar
Qin, Y. et al. Carbon loss from forest degradation exceeds that from deforestation in the Brazilian Amazon. Nat. Clim. Chang. 11, 442–448 (2021).
Article ADS MATH Google Scholar
Roebroek, C. T. J., Duveiller, G., Seneviratne, S. I., Davin, E. L. & Cescatti, A. Releasing global forests from human management: how much more carbon could be stored? Science 380, 749–753 (2023).
Article ADS CAS PubMed Google Scholar
Bonan, G. B. Forests and climate change: forcings, feedbacks, and the climate benefits of forests. Science 320, 1444–1449 (2008).
Article ADS CAS PubMed MATH Google Scholar
Lawrence, D., Coe, M., Walker, W., Verchot, L. & Vandecar, K. The unseen effects of deforestation: biophysical effects on climate. Front. Glob. Chang. 5, 1–13 (2022).
Article Google Scholar
Pearce, F. The forest forecast. Science 376, 788–791 (2022).
Article ADS PubMed MATH Google Scholar
Li, Y. et al. Local cooling and warming effects of forests based on satellite observations. Nat. Commun. 6, 1–10 (2015).
ADS MATH Google Scholar
Alkama, R. & Cescatti, A. Biophysical climate impacts of recent changes in global forest cover. Science 351, 600–604 (2016).
Article ADS CAS PubMed Google Scholar
Pongratz, J. et al. Land use effects on climate: current state, recent progress, and emerging topics. Curr. Clim. Chang. Rep. 7, 99–120 (2021).
Article MATH Google Scholar
Winckler, J., Lejeune, Q., Reick, C. H. & Pongratz, J. Nonlocal effects dominate the global mean surface temperature response to the biogeophysical effects of deforestation. Geophys. Res. Lett. 46, 745–755 (2019).
Article ADS Google Scholar
Winckler, J., Reick, C. H. & Pongratz, J. Why does the locally induced temperature response to land cover change differ across scenarios? Geophys. Res. Lett. 44, 3833–3840 (2017).
Article ADS MATH Google Scholar
Davin, E. L. & de Noblet-Ducoudre, N. Climatic impact of global-scale Deforestation: Radiative versus nonradiative processes. J. Clim. 23, 97–112 (2010).
Article ADS MATH Google Scholar
Bala, G. et al. Combined climate and carbon-cycle effects of large-scale deforestation. Proc. Natl. Acad. Sci. USA 104, 6550–6555 (2007).
Article ADS CAS PubMed PubMed Central MATH Google Scholar
Lu, N. et al. Biophysical and economic constraints on China’s natural climate solutions. Nat. Clim. Chang. 12, 847–853 (2022).
Article ADS MATH Google Scholar
Nanni, A. S. et al. The neotropical reforestation hotspots: a biophysical and socioeconomic typology of contemporary forest expansion. Glob. Environ. Chang. 54, 148–159 (2019).
Article MATH Google Scholar
Ge, J. et al. Local surface cooling from afforestation amplified by lower aerosol pollution. Nat. Geosci. 16, 781–788 (2023).
Windisch, M. G., Davin, E. L. & Seneviratne, S. I. Prioritizing forestation based on biogeochemical and local biogeophysical impacts. Nat. Clim. Chang. 11, 867–871 (2021).
Article ADS CAS MATH Google Scholar
Zhu, L. et al. Comparable biophysical and biogeochemical feedbacks on warming from tropical moist forest degradation. Nat. Geosci. 16, 244–249 (2023).
Article ADS CAS MATH Google Scholar
Winckler, J., Reick, C. H. & Pongratz, J. Robust identification of local biogeophysical effects of land-cover change in a global climate model. J. Clim. 30, 1159–1176 (2017).
Article ADS MATH Google Scholar
Li, Y., Piao, S., Chen, A., Ciais, P. & Li, L. Z. X. Local and teleconnected temperature effects of afforestation and vegetation greening in China. Natl Sci. Rev. 7, 897–912 (2020).
Article PubMed MATH Google Scholar
Pitman, A. J. et al. Uncertainties in climate responses to past land cover change: first results from the LUCID intercomparison study. Geophys. Res. Lett. 36, 1–6 (2009).
Article MATH Google Scholar
Luo, X. et al. An evaluation of CMIP6 models in representing the biophysical effects of deforestation with satellite‐based observations. J. Geophys. Res. Atmos. 128, 1–20 (2023).
Article MATH Google Scholar
Duveiller, G. et al. Biophysics and vegetation cover change: a process-based evaluation framework for confronting land surface models with satellite observations. Earth Syst. Sci. Data 10, 1265–1279 (2018).
Article ADS MATH Google Scholar
Su, Y. et al. Asymmetric influence of forest cover gain and loss on land surface temperature. Nat. Clim. Chang. 13, 823–831 (2023).
Article ADS MATH Google Scholar
Bright, R. M. et al. Local temperature response to land cover and management change driven by non-radiative processes. Nat. Clim. Chang. 7, 296–302 (2017).
Article ADS MATH Google Scholar
Liu, X. et al. Local temperature responses to actual land cover changes present significant latitudinal variability and asymmetry. Sci. Bull. 68, 2849–2861 (2023).
Article ADS MATH Google Scholar
Li, Y. et al. Biophysical impacts of earth greening can substantially mitigate regional land surface temperature warming. Nat. Commun. 14, 121 (2023).
Article ADS PubMed PubMed Central MATH Google Scholar
Butt, E. W. et al. Amazon deforestation causes strong regional warming. Proc. Natl. Acad. Sci. USA 120, 2017 (2023).
Article MATH Google Scholar
Zhang, Q. et al. Reforestation and surface cooling in temperate zones: mechanisms and implications. Glob. Chang. Biol. 26, 3384–3401 (2020).
Article ADS PubMed MATH Google Scholar
Intergovernmental Panel on Climate Change. Changing State of the Climate System. In Climate Change 2021—The Physical Science Basis 287–422 (Cambridge University Press, 2023).
Wang, Y. R., Hessen, D. O., Samset, B. H. & Stordal, F. Evaluating global and regional land warming trends in the past decades with both MODIS and ERA5-Land land surface temperature data. Remote Sens. Environ. 280, 113181 (2022).
Article Google Scholar
Mildrexler, D. J., Zhao, M. & Running, S. W. A global comparison between station air temperatures and MODIS land surface temperatures reveals the cooling role of forests. J. Geophys. Res. Biogeosci. 116, 1–15 (2011).
Article Google Scholar
Novick, K. A. & Katul, G. G. The duality of reforestation impacts on surface and air temperature. J. Geophys. Res. Biogeosci. 125, 1–15 (2020).
Article MATH Google Scholar
Winckler, J. et al. Different response of surface temperature and air temperature to deforestation in climate models. Earth Syst. Dyn. 10, 473–484 (2019).
Article ADS MATH Google Scholar
Baldocchi, D. & Ma, S. How will land use affect air temperature in the surface boundary layer? Lessons learned from a comparative study on the energy balance of an oak savanna and annual grassland in California, USA. Tellus. Ser. B Chem. Phys. Meteorol. 65, 1–19 (2013).
Google Scholar
Lee, X. et al. Observed increase in local cooling effect of deforestation at higher latitudes. Nature 479, 384–387 (2011).
Article ADS CAS PubMed MATH Google Scholar
Peng, S. S. et al. Afforestation in China cools local land surface temperature. Proc. Natl. Acad. Sci. USA 111, 2915–2919 (2014).
Article ADS CAS PubMed PubMed Central MATH Google Scholar
Reiners, P., Sobrino, J. & Kuenzer, C. Satellite-derived land surface temperature dynamics in the context of global change—a review. Remote Sens. 15, 1857 (2023).
Pastorello, G. et al. The FLUXNET2015 dataset and the ONEFlux processing pipeline for eddy covariance data. Sci. Data 7, 1–27 (2020).
Article MATH Google Scholar
Duveiller, G., Hooker, J. & Cescatti, A. The mark of vegetation change on Earth’s surface energy balance. Nat. Commun. 9, 64–75 (2018).
Article Google Scholar
Schultz, N. M., Lawrence, P. J. & Lee, X. Global satellite data highlights the diurnal asymmetry of the surface temperature response to deforestation. J. Geophys. Res. Biogeosci. 122, 903–917 (2017).
Article MATH Google Scholar
Zhong, Z. et al. Reversed asymmetric warming of sub-diurnal temperature over land during recent decades. Nat. Commun. 14, 1–10 (2023).
Article ADS MATH Google Scholar
Lian, X. et al. Spatiotemporal variations in the difference between satellite-observed daily maximum land surface temperature and station-based daily maximum near-surface air temperature. J. Geophys. Res. 122, 2254–2268 (2017).
Article MATH Google Scholar
Chen, C. et al. Biophysical impacts of Earth greening largely controlled by aerodynamic resistance. Sci. Adv. 6, 1–10 (2020).
Article CAS MATH Google Scholar
Lin, H., Li, Y. & Zhao, L. Partitioning of sensible and latent heat fluxes in different vegetation types and their spatiotemporal variations based on 203 FLUXNET sites. J. Geophys. Res. Atmos. 127, e2022JD037142 (2022).
Walker, W. S. et al. The global potential for increased storage of carbon on land. Proc. Natl. Acad. Sci. USA 119, 1–12 (2022).
Article MATH Google Scholar
Lewis, S. L., Wheeler, C. E., Mitchard, E. T. A. & Koch, A. Restoring natural forests is the best way to remove atmospheric carbon. Nature 568, 25–28 (2019).
Article ADS CAS PubMed MATH Google Scholar
Zhao, K. & Jackson, R. B. Biophysical forcings of land-use changes from potential forestry activities in North America. Ecol. Monogr. 84, 329–353 (2014).
Article MATH Google Scholar
Portmann, R. et al. Global forestation and deforestation affect remote climate via adjusted atmosphere and ocean circulation. Nat. Commun. 13, 1–11 (2022).
Article MATH Google Scholar
Hoek van Dijke, A. J. et al. Shifts in regional water availability due to global tree restoration. Nat. Geosci. 15, 363–368 (2022).
Article ADS CAS Google Scholar
He, M. et al. Amplified warming from physiological responses to carbon dioxide reduces the potential of vegetation for climate change mitigation. Commun. Earth Environ. 3, 1–10 (2022).
Article ADS MATH Google Scholar
Deng, L., Zhu, G. Y., Tang, Z. S. & Shangguan, Z. P. Global patterns of the effects of land-use changes on soil carbon stocks. Glob. Ecol. Conserv. 5, 127–138 (2016).
Google Scholar
Sanderman, J., Hengl, T. & Fiske, G. J. Soil carbon debt of 12,000 years of human land use. Proc. Natl. Acad. Sci. USA 114, 9575–9580 (2017).
Article ADS CAS PubMed PubMed Central MATH Google Scholar
Guo, L. B. & Gifford, R. M. Soil carbon stocks and land use change: a meta analysis. Glob. Chang. Biol. 8, 345–360 (2002).
Article ADS MATH Google Scholar
Mo, L. et al. Integrated global assessment of the natural forest carbon potential. Nature 624, 92–101 (2023).
Article ADS CAS PubMed PubMed Central MATH Google Scholar
Li, Y. et al. Prioritizing Forestation in China Through Incorporating Biogeochemical and Local Biogeophysical Effects. Earth’s. Futur. 12, 1–18 (2024).
Article Google Scholar
Veldman, J. W. et al. Comment on “The global tree restoration potential. Science 366, 1–5 (2019).
Article MATH Google Scholar
Guo, Z. et al. Does plant ecosystem thermoregulation occur? An extratropical assessment at different spatial and temporal scales. New Phytol. 238, 1004–1018 (2022).
Hasler, N. et al. Accounting for albedo change to identify climate-positive tree cover restoration. Nat. Commun. 15, 2275 (2024).
Article ADS CAS PubMed PubMed Central MATH Google Scholar
Weber, J. et al. Chemistry-albedo feedbacks offset up to a third of forestation’s CO₂ removal benefits. Science 383, 860–864 (2024).
Article ADS CAS PubMed MATH Google Scholar
Barnes, M. L. et al. A century of reforestation reduced anthropogenic warming in the Eastern United States. Earth’s Futur. 12, e2023EF003663 (2024).
Bond, W. J., Stevens, N., Midgley, G. F. & Lehmann, C. E. R. The trouble with trees: afforestation plans for Africa. Trends Ecol. Evol. 34, 963–965 (2019).
Article PubMed Google Scholar
Bond, W. J. Ancient grasslands at risk. Science 351, 120–122 (2016).
Article ADS CAS PubMed MATH Google Scholar
Gómez-González, S., Ochoa-Hueso, R. & Pausas, J. G. Afforestation falls short as a biodiversity strategy. Science 368, 1439–1439 (2020).
Article ADS PubMed Google Scholar
Parr, C. L., te Beest, M. & Stevens, N. Conflation of reforestation with restoration is widespread. Science 383, 698–701 (2024).
Article ADS CAS PubMed MATH Google Scholar
Selva, N., Chylarecki, P., Jonsson, B.-G. & Ibisch, P. L. Misguided forest action in EU Biodiversity Strategy. Science 368, 1438–1439 (2020).
Article ADS PubMed Google Scholar
Liu, Y. et al. Global mapping of fractional tree cover for forest cover change analysis. ISPRS J. Photogramm. Remote Sens. 211, 67–82 (2024).
Article ADS MATH Google Scholar
Hansen, M. C. et al. High-resolution global maps of 21st-century forest cover change. Science 342, 850–853 (2013).
Article ADS CAS PubMed MATH Google Scholar
Xing, Z. et al. Estimation of daily mean land surface temperature at global scale using pairs of daytime and nighttime MODIS instantaneous observations. ISPRS J. Photogramm. Remote Sens. 178, 51–67 (2021).
Article ADS MATH Google Scholar
Liu, X. et al. Temporal upscaling of MODIS 1-km instantaneous land surface temperature to monthly mean value: method evaluation and product generation. IEEE Trans. Geosci. Remote Sens. 61, 1–14 (2023).
Article CAS Google Scholar
Zhang, T. et al. A global dataset of daily maximum and minimum near-surface air temperature at 1 km resolution over land (2003–2020). Earth Syst. Sci. Data 14, 5637–5649 (2022).
Article ADS MATH Google Scholar
Zhang, T., Zhou, Y., Wang, L., Zhao, K. & Zhu, Z. Estimating 1 km gridded daily air temperature using a spatially varying coefficient model with sign preservation. Remote Sens. Environ. 277, 113072 (2022).
Article MATH Google Scholar
Keenan, R. J. et al. Dynamics of global forest area: results from the FAO Global Forest Resources Assessment 2015. For. Ecol. Manag. 352, 9–20 (2015).
Article MATH Google Scholar
Pekel, J. F., Cottam, A., Gorelick, N. & Belward, A. S. High-resolution mapping of global surface water and its long-term changes. Nature 540, 418–422 (2016).
Article ADS CAS PubMed MATH Google Scholar
Zhang, Y. et al. Asymmetric impacts of forest gain and loss on tropical land surface temperature. Nat. Geosci. 13, 823–831 (2024).
MATH Google Scholar
Wang, H., Yue, C. & Luyssaert, S. Reconciling different approaches to quantifying land surface temperature impacts of afforestation using satellite observations. Biogeosciences 20, 75–92 (2023).
Article ADS MATH Google Scholar
Chen, L., Dirmeyer, P. A., Guo, Z. & Schultz, N. M. Pairing FLUXNET sites to validate model representations of land-use/land-cover change. Hydrol. Earth Syst. Sci. 22, 111–125 (2018).
Article ADS Google Scholar
Novick, K. A. & Barnes, M. L. A practical exploration of land cover impacts on surface and air temperature when they are most consequential. Environ. Res. Clim. 2, 025007 (2023).
Article ADS MATH Google Scholar
Harris, I., Osborn, T. J., Jones, P. & Lister, D. Version 4 of the CRU TS monthly high-resolution gridded multivariate climate dataset. Sci. Data 7, 1–18 (2020).
Article Google Scholar
Rohde, R. A. & Hausfather, Z. The Berkeley earth land/ocean temperature record. Earth Syst. Sci. Data 12, 3469–3479 (2020).
Article ADS MATH Google Scholar
Duan, S. B. et al. Validation of collection 6 MODIS land surface temperature product using in situ measurements. Remote Sens. Environ. 225, 16–29 (2019).
Article ADS MATH Google Scholar
Juang, J. Y., Katul, G., Siqueira, M., Stoy, P. & Novick, K. Separating the effects of albedo from eco-physiological changes on surface temperature along a successional chronosequence in the southeastern United States. Geophys. Res. Lett. 34, 1–5 (2007).
Article Google Scholar
Monin, A. S. & Obukhov, A. M. Basic laws of turbulent mixing in the surface layer of the atmosphere. Contrib. Geophys. Inst. Acad. Sci. USSR 24, 163–187 (1954).
MATH Google Scholar
Peng, Z., Tang, R., Jiang, Y., Liu, M. & Li, Z.-L. Global estimates of 500 m daily aerodynamic roughness length from MODIS data. ISPRS J. Photogramm. Remote Sens. 183, 336–351 (2022).
Article ADS MATH Google Scholar
Rigden, A., Li, D. & Salvucci, G. Dependence of thermal roughness length on friction velocity across land cover types: a synthesis analysis using AmeriFlux data. Agric. Meteorol. 249, 512–519 (2018).
Article Google Scholar
Xu, H., Yue, C., Zhang, Y., Liu, D. & Piao, S. Forestation at the right time with the right species can generate persistent carbon benefits in China. Proc. Natl. Acad. Sci. USA 120, 2017 (2023).
Article MATH Google Scholar
Spawn, S. A., Sullivan, C. C., Lark, T. J. & Gibbs, H. K. Harmonized global maps of above and belowground biomass carbon density in the year 2010. Sci. Data 7, 1–22 (2020).
Article Google Scholar

Download references

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant No. 41921001, Z.-L.L.; 42071331, H.W.), the Strategic Priority Research Program of Chinese Academy of Sciences (Grant No. XDA28050200, H.W.). The authors acknowledge constructive and insightful comments from Prof. Ronggao Liu and Prof. Yang Liu. The authors give our sincere thanks to all data providers for their continuous efforts and sharing the data.

Author information

Authors and Affiliations

State Key Laboratory of Resources and Environment Information System, Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing, China
Yitao Li & Ronglin Tang
University of Chinese Academy of Sciences, Beijing, China
Yitao Li, Ronglin Tang & Xiaoning Song
State Key Laboratory of Efficient Utilization of Arable Land in China, Institute of Agricultural Resources and Regional Planning, Chinese Academy of Agricultural Sciences, Beijing, China
Zhao-Liang Li, Xiangyang Liu, Menglin Si, Jing Li, Sibo Duan & Pei Leng
School of Resources and Environment, University of Electronic Science and Technology of China, Chengdu, China
Hua Wu
Department of Earth and Environmental Engineering, Columbia University, New York, NY, USA
Xu Lian
Center for Ocean Remote Sensing of Southern Marine Science and Engineering Guangdong Laboratory (Guangzhou), Guangzhou Institute of Geography, Guangdong Academy of Sciences, Guangzhou, China
Chenghu Zhou
Institute of Mountain Hazards and Environment, Chinese Academy of Sciences, Chengdu, China
Wei Zhao
School of Geography and Planning, Sun Yat-sen University, Guangzhou, China
Qian Shi
College of Information Science and Technology, Dalian Maritime University, Dalian, China
Enyu Zhao
Key Laboratory of Quantitative Remote Sensing Information Technology, Aerospace Information Research Institute, Chinese Academy of Sciences, Beijing, China
Caixia Gao

Authors

Yitao Li
View author publications
You can also search for this author inPubMed Google Scholar
Zhao-Liang Li
View author publications
You can also search for this author inPubMed Google Scholar
Hua Wu
View author publications
You can also search for this author inPubMed Google Scholar
Xiangyang Liu
View author publications
You can also search for this author inPubMed Google Scholar
Xu Lian
View author publications
You can also search for this author inPubMed Google Scholar
Menglin Si
View author publications
You can also search for this author inPubMed Google Scholar
Jing Li
View author publications
You can also search for this author inPubMed Google Scholar
Chenghu Zhou
View author publications
You can also search for this author inPubMed Google Scholar
Ronglin Tang
View author publications
You can also search for this author inPubMed Google Scholar
Sibo Duan
View author publications
You can also search for this author inPubMed Google Scholar
Wei Zhao
View author publications
You can also search for this author inPubMed Google Scholar
Pei Leng
View author publications
You can also search for this author inPubMed Google Scholar
Xiaoning Song
View author publications
You can also search for this author inPubMed Google Scholar
Qian Shi
View author publications
You can also search for this author inPubMed Google Scholar
Enyu Zhao
View author publications
You can also search for this author inPubMed Google Scholar
Caixia Gao
View author publications
You can also search for this author inPubMed Google Scholar

Contributions

Y.L., Z.-L.L., and H.W. conceived and designed the research. Y.L. and X. Liu organized and processed the data. Y.L., X. Liu, M.S., and J.L. carried out the analysis. Y.L. drafted the paper. Z.-L.L., H.W., X. Lian, C.Z., R.T., S.D., W.Z., P.L., X.S., Q.S., E.Z., and C.G. edited and revised the manuscript.

Corresponding author

Correspondence to Zhao-Liang Li.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Communications thanks Konstantin Gregor and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Transparent Peer Review file

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.

Reprints and permissions

About this article

Cite this article

Li, Y., Li, ZL., Wu, H. et al. Observed different impacts of potential tree restoration on local surface and air temperature. Nat Commun 16, 2335 (2025). https://doi.org/10.1038/s41467-025-57606-y

Download citation

Received: 29 April 2024
Accepted: 19 February 2025
Published: 08 March 2025
DOI: https://doi.org/10.1038/s41467-025-57606-y