The past, present, and future evolution of Aurora Subglacial Basin’s subglacial drainage system

Abstract

Aurora Subglacial Basin (ASB) in East Antarctica is among the most rapidly changing regions in Antarctica. Beneath the ASB, subglacial drainage networks allow for fast ice flow and facilitate mass losses by eroding the coastal ice shelves. The ASB underwent advance-retreat cycles since its inception 34 million years ago, and projections rely on these findings to predict future ice behaviour. Yet, these hindcasts and forecasts seldom consider the effects of subglacial drainage. Here, we model subglacial drainage networks and ice shelf basal melting of the ASB from 34 million years ago to 2100 CE. Our results indicate continual reorganisation of ASB drainage systems and ice shelf melt patterns, suggesting that the past does not fully serve as an analogue for the future. Since subglacial drainage accounts for up to 70% of ice shelf melt, our results imply that subglacial hydrology could trigger higher rates of mass loss than previously suggested.

Introduction

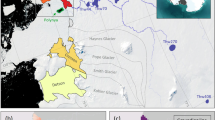
Ongoing climate warming has signalled concern about the fate of the Antarctic Ice Sheet and future sea levels, especially since the East Antarctic Ice Sheet contains 52 m of potential sea level rise¹, the largest of all modern-day ice reservoirs. Within East Antarctica, Totten Glacier, in the Aurora Subglacial Basin (ASB, Fig. 1), is rapidly changing, displaying both the highest grounded ice thinning rates and highest rates of ice discharge of all East Antarctic outlet glaciers². This area contains an ice volume equivalent of 3.9 m of sea level rise¹ and is currently in a state of negative mass balance³. In recent decades, Totten Glacier has experienced periods of accelerated ice flow velocities, ice thinning, and grounding line retreat^{2,3,4,5,6,7,8}. These changes are associated with intrusions of warm, modified Circumpolar Deep Water^5,7,8,9,10 (mCDW), which erodes Totten Glacier’s Ice Shelf, the floating portion of Totten Glacier that serves as a girdle on ice flow.

Fig. 1: Aurora Subglacial Basin model domains and basal input data.

a shows the Ice Sheet Model Intercomparison Project for CMIP6 basal velocities (ISMIP6²⁵) with the black rectangle indicating the study region and the pink rectangle outlining the region shown in (c–l). b shows the zoom-in from (a), with domain outlines for each time snapshot shown by the coloured lines. c–g show the bed topography in metres (m). h–l show the basal meltwater production rate in mm a⁻¹, with the 50 ma⁻¹ basal velocity contour shown as a red dashed line. Eocene–Oligocene Boundary (34 million years ago) data are shown in (c, h); Mid-Miocene data in (d, i); present-day data in (e, j); maximum ice loss at 2100 CE in (f, k); data in (g, l) correspond to the maximum ice gain scenario at 2100 CE. Full domain maps of bed and surface elevation are included in the Supplementary Information (Figs. S2–S6). Source data are provided as a Source data file.

Totten Glacier and the ASB may be inherently unstable due to a large proportion of the ice in the region grounded below sea level on a reverse bed slope^1,11, making it susceptible to the Marine Ice Sheet Instability¹² (MISI). Furthermore, collapse of buttressing ice shelves and unstoppable grounding line retreat may occur if the Marine Ice Cliff Instability (MICI) is set in motion due to ice shelf hydrofracture and ice cliff failure¹³. Models that include MICI suggest some of the highest projected ice losses and sea level rise estimates, but since there is limited observational evidence of past MICI behaviour¹⁴ and large uncertainties in MICI processes¹⁵, the plausibility of MICI continues to be debated. In the ASB, including MICI in modelled projections can cause thousands of square kilometres of grounded ice to be lost (Fig. S7). Regardless of the potential impacts of MICI, it is likely that mCDW will continue to affect ASB’s glaciers over the next century and push grounding lines farther inland, with the magnitude and extent of this retreat dependent on greenhouse gas emissions¹⁶. This situation could be exacerbated if instability mechanisms were to be initiated. Still, since most ice sheet models neglect evolving subglacial hydrology, it has seldom been considered that changes to subglacial drainage systems may be sufficient to initiate large-scale ice dynamic and geometric changes without the need for MICI.

The future trajectory of ice loss in ASB could potentially resemble that from the geologic past when climate conditions were similar to those predicted for the coming decades and centuries^13,17. It has been suggested that the dynamic behaviour of the paleo-ASB can partially be explained by the subglacial drainage network configuration^18,19,20. Present-day subglacial drainage in the ASB consists of a network of long, high-pressure channels that reach far into the interior of the ASB²¹. These channels play a critical role in regulating the flow of the overlying ice, while also pumping large volumes of freshwater beneath ice shelves, facilitating high and localised ice shelf basal melt rates²². If the volume of discharge exiting these channels, or their locations, were to change, there could be far-reaching impacts on the stability of ice flow in the ASB, such as accelerations of ice velocities and grounding line retreat rates²³. However, there has not been a focused study on evolving subglacial drainage in the ASB during previous warm periods, how hydrology will be configured in future warm conditions, and the associated consequences of these changes for ice dynamics and ice shelf basal melt rates.

Here, we use the 2D, finite-element Glacier Drainage System²⁴ (GlaDS, described in Methods) subglacial hydrology model to assess how ice sheet geometry at different time snapshots in the past and future affect the subglacial hydrology of the ASB’s grounded ice and infer the effects on ice shelf basal melt rates. We consider different concentrations of greenhouse gases and the impact of the MICI mechanism on the channel network and drainage system pressurisation. We show that there has been substantial reorganisation of the ASB’s basal hydrological network since the inception of the Antarctic Ice Sheet 34 million years ago, and that drainage will continue to evolve over the next century in response to climate warming.

Results

Present-day subglacial hydrology

We first simulate modern-day subglacial hydrology using bed topography from BedMachine Antarctica¹ and basal velocities and meltwater production rates from the Ice Sheet Model Intercomparison Project for CMIP6 (ISMIP6²⁵). With these datasets, we have revised and expanded the domain used in Dow et al.²¹ to capture upglacier activity and facilitate the comparison between our paleo and future simulations. Since Dow et al.’s²¹ model outputs were validated by radar-derived specularity content data, we consider their model outputs to be a benchmark for our model runs. We therefore adopt the same parameter values as used in Dow et al.’s²¹ base model run for bedrock obstacle sizes and distributed and channelised system conductivities. Like in Dow et al.²¹, we find that channel discharges are greatest through Totten Glacier, with fluxes reaching 33 m³s^-1 from the entire section of Totten’s grounding line (Fig. 2c). High water pressure occurs in the upland regions, another similarity between our simulations and those in Dow et al.²¹. Due to the high level of agreement between our modern-day results and those of Dow et al.’s²¹, the remainder of this paper focuses on how paleo and future subglacial hydrology compares to the contemporary drainage system. We direct readers to Dow et al.²¹ for an in-depth analysis of the present-day drainage system of the ASB.

Fig. 2: Modelled subglacial channel discharge from paleo, modern, and future time snapshots.

Panels show the channel discharge under grounded ice at a the Eocene–Oligocene Boundary; b the Mid-Miocene; c present day; d 2100 CE, under maximum volumes of ice loss; and e 2100 CE under maximum volumes of ice gain. Black lines show the grounding lines, where water exits the domain, for each simulation. Dotted lines and abbreviations point to glacier locations. B Bond Glacier, MU Moscow University Ice Shelf, T Totten Glacier, V Vanderford Glacier. Channel discharge for each glacier labelled in the figure panels at each time snapshot is included in the supplementary material (Figs. S8–S12). Source data are provided as a Source data file.

Paleo subglacial hydrology

Our paleo subglacial hydrology simulations use grounding lines, ice sheet geometries, and basal inputs from Paxman et al.²⁶. We focus on the Eocene-Oligocene Boundary (34 Mya) and the Mid-Miocene Climate Transition (14 Mya; hereafter Mid-Miocene) as these intervals correspond to ice volumes in ASB that are larger and smaller, respectively, than those in the present day²⁶. The purpose of these experiments is to provide a large-scale overview of how changes in ice configurations and basal (melt, velocity, and topography) conditions influence ASB’s subglacial drainage system and are not intended to be interpreted as the exact subglacial conditions during each of these paleo time snapshots. In the Discussion, we compare our model results to geomorphological evidence.

Here, we focus on the subglacial hydrology and ice shelf basal melting results produced by adopting the ice geometries from Paxman et al.’s²⁶ “No MICI, 500 ppm CO₂” experiments. This level of CO₂ represents (a) the likely lower bound during the Eocene-Oligocene Boundary, (b) the likely upper bound for the Mid-Miocene, and (c) the possible CO₂ concentration for the future^{27,28,29,30,31,32,33,34}. Due to limited observational evidence and divided findings from modelling efforts, is not yet clear if MICI has occurred in the geologic past and if it will occur in the next centuries^14,15. We discuss how the ice geometries from Paxman et al.’s²⁶ MICI and low CO₂ experiments affect our results in the section titled “Carbon emissions and instability processes influence drainage morphology”.

Our Eocene-Oligocene Boundary results indicate that channels grew up to 370 km long (Fig. 2a), more than twice the length of present-day channels in the ASB (Fig. 2c and Dow et al.²¹). Nearly 160 m³s^-1 of channelised discharge exits the subglacial drainage system at the grounding line, shared between 9 outlet channels. 95% of this discharge is sourced from channels draining across Totten Glacier’s grounding line rather than the nearby Vanderford and Bond Glaciers. One of Totten’s channels pumps 117 m³s^-1 of freshwater into the ice shelf cavity, accounting for 75% of ASB’s cumulative grounding line discharge. Discharge from this channel alone exceeds the cumulative grounding line discharge from ASB’s current drainage system by 40 m³s^-1. All channels are fed by regions with water around ice overburden pressure. However, channels do not substantially reduce water pressure, and are within 5% of ice overburden pressure, consistent with modelling of present-day channels²¹. 95.47% of the domain is at or above 95% of ice overburden pressure; the highest proportion of all simulations.

We find a close correspondence with high pressure regions (Fig. 3) and thick (≥0.08 m) water sheets. These thicker sheets tend to be in basal troughs (Fig. S1) and show agreement with the upglacier initiation points of small channels. We do not observe an overlap between large water sheet thicknesses and high basal velocities or basal meltwater production rates. Since we do not couple our subglacial hydrology model to an ice sheet model, we use the basal meltwater production rates and basal velocities determined by Paxman et al.²⁶ as inputs into our model. The highest velocities occur beneath Totten Glacier, which we capped at 800 ma^-1 to prevent model instabilities (Table S1). Basal meltwater production rates beneath Totten Glacier reach 2 ma^-1 at the grounding line, which is nearly six times larger than the present-day meltwater production rate at the grounding line²¹. Meltwater production remains elevated (≥10 cma^-1) up to 160 km from the grounding line, beyond which it approaches the catchment-wide mean of 6 mma^-1, exceeding the present-day catchment-wide average by 2.3 mma^-1. Overall, these results suggest spatially-variable controls on drainage beneath ASB. Topographic controls and basal melting have a greater influence on subglacial drainage upglacier, whereas high basal velocities and meltwater production rates play a dominant role in drainage morphology beneath Totten Glacier and closer to the grounding line. We performed sensitivity tests to determine the relative influence of bed and surface topography, basal melt, and basal velocity (Text S1). These tests indicated that the ice surface geometry is the primary control on where dominant drainage pathways form, but that changes in bed topography can influence channel lengths. Varying basal meltwater production rates and velocities caused more than a 10-fold change in grounding line channel fluxes and changes in the distribution and extent of high-pressure regions, both of which can affect ice dynamics through their influence ice shelf basal melt rates and on ice velocities, respectively.

Fig. 3: Modelled subglacial water pressure as a fraction of ice overburden from paleo, modern, and future time snapshots.

. Panels show the model outputs at a the Eocene–Oligocene Boundary; b the Mid-Miocene; c present day; d 2100 CE, under maximum amounts of ice loss; and e 2100 CE under maximum amounts of ice gain. Black lines show the grounding lines for each simulation. Yellow contours indicate the regions at and above ice overburden pressure. Source data are provided as a Source data file.

In the Mid-Miocene, similar to the Eocene-Oligocene Boundary, high water pressures and thick water sheets are coincident and form in basal troughs. The largest channels also occur where basal velocities and rates of basal meltwater production are highest. Beyond this, the subglacial drainage morphology during the Mid-Miocene differs substantially from that at the Eocene-Oligocene Boundary. For instance, the maximum channel length for the Mid-Miocene is 270 km long (Fig. 2b), 100 km shorter than the longest channel in our Eocene-Oligocene runs (although ~100 km longer than present-day channels; Fig. 2c and Dow et al.²¹). The Mid-Miocene channels pump 35 m³s^-1 less water across the grounding line than the channels in the Eocene-Oligocene drainage system. However, there are more channels crossing the grounding line in the Mid-Miocene run since the ice in this simulation has retreated past Law Dome. This pattern of ice retreat results in a grounding line channel density (number of channels per km of grounding line) that is ~3.4 times higher than that of the Eocene-Oligocene Boundary. This suggests that retreat past Law Dome can trigger, or at least contribute to, reorganisation of water flow, as well as determining where the majority of the water exits the domain. We find that during the Mid-Miocene, discharge over the section of grounding line near Totten Glacier is relatively small compared to our Eocene-Oligocene simulations, and accounts for only a third of the total grounding line discharge. During the Mid-Miocene, our results indicate that the largest discharge crossing the grounding line occurs near the former location of Law Dome. Across this section of the grounding line, the maximum channel discharge is ~29 m³s^-1, with a cumulative channel discharge of 58.29 m³s^-1 in this region, which accounts for nearly half of the total channelised grounding line discharge.

Future subglacial hydrology

We next investigate the possible subglacial drainage morphologies of the ASB at 2100 CE, using ice geometries from Li et al.³⁵, who considered how the spectrum of CMIP6 climate forcing impacts Antarctic Ice Sheet evolution. We selected the Li et al.³⁵ ice geometries from CMIP6 forcings that resulted in the greatest ice loss (NorESM2-MM) and the largest ice gain (CMCC-CM2-SR5), representing end-member scenarios for ASB. Similar to our paleo experiments, we run two sets of simulations for each CMIP6 forcing, one in which the ice geometry was generated with MICI processes turned on, and one where these processes were excluded. The results from the MICI runs are presented in the supplementary information.

The degree of similarity of future subglacial drainage to present or past drainage networks is highly dependent on ice surface slope changes. For the maximum ice gain scenario, grounding line channel discharge at 2100 CE (Fig. 2e) is of a similar magnitude to the present (Fig. 2c, Table S3 and Dow et al.²¹) and has similar grounding line channel density. However, channels are up to 100 km longer in this future scenario. Under high rates of ice loss (Fig. 2d), channel length (303 km), discharges (163 m³s^-1), and grounding line channel density (0.0108 channels per km of groundling line) resemble that of the Eocene-Oligocene Boundary, albeit the organisation of the drainage system is more branching in the future simulation. These channel lengths, discharges, and densities are more than twice that of the present-day. For both future scenarios, most of the discharge exits at the grounding lines of Moscow University Ice Shelf and Totten Glaciers. However, while Totten Glacier accounted for three-quarters of total discharge during the Eocene-Oligocene Boundary, at 2100 CE, it only accounts for 35% of the grounding line discharge. This suggests that the changes in ice and bed geometry over time favour a more arborescent channelised drainage network. Furthermore, relative to the present-day simulation, we find that the partitioning of drainage in both of our future simulations tends to favour greater discharges beneath Bond and Vanderford Glaciers.

We find substantial differences between the channel discharges for the two future scenarios. The maximum ice loss scenario results in more than twice the channel density and discharge at the grounding line compared to the maximum ice gain scenario (0.0108 channels per km of groundling line for the maximum ice loss scenario versus 0.0053 channels per km of grounding line for the maximum ice gain scenario). The discharge velocity (channel flux divided by channel cross-sectional area) of the largest channel from the maximum ice loss scenario is 0.9741 ms^-1, >30% faster than that observed in the maximum ice gain scenario (0.6347 ms^-1) and >40 times faster than that from the Eocene-Oligocene (0.0233 ms^-1). The steep surface slopes of the maximum ice loss run, especially near the grounding line, lead to higher hydraulic potential gradients (Fig. S13) that cause high basal velocities and meltwater production rates. Consequently, discharge volumes and associated water velocities are much larger than the other simulations, which drive enhanced rates of ice shelf basal melting at deep grounding line points by locally increasing rates of turbulent sub-ice shelf ocean mixing near the discharge outflow locations. We discuss these implications in the section titled “Ice shelf basal melt impacts”.

Similar to our paleo and present-day runs, our water pressure results for the future runs indicate that high pressures continue to persist in basal depressions. Compared to the paleo simulations, the region where water pressures reach or exceed ice overburden pressure (yellow contours in Fig. 3) has migrated further inland. These upland regions of over-pressured troughs do not occur in the present-day run. It is likely that erosion of the bed since the Eocene-Oligocene Boundary has heightened ASB’s sensitivity to climate-driven retreat²⁶. Our simulations indicate that these bed changes over time have also influenced the distribution of subglacial water pressures and primary subglacial drainage pathways and support the findings of Wright et al.³⁶ who suggested that a basal trough that meanders inland and near Totten Glacier connects upglacier subglacial drainage to the downstream drainage system. Our results show that pressures remain above overburden in the upland region, which, if using water pressure as a proxy for ice velocity, suggests that fast velocities may migrate further inland in the future.

Carbon emissions and instability processes influence drainage morphology

We also tested how paleo ice configurations that resulted from lower CO₂ levels affected our outputs (Figs. S14–S21). Channels in our low (280 ppm) CO₂ simulations were up to 37 km shorter than those from the 500 ppm simulations, with nearly 60 m³s^-1 less total grounding line discharge. Since the ice has not retreated as far back in the low CO₂ simulations (Figs. S14–S15), the grounding line channel density is lower. This difference is most prominent in the Mid-Miocene 280 ppm No MICI run, where the grounding line channel density is half that of the 500 ppm simulation. Mean channel pressure in our low CO₂ No MICI runs is also slightly lower (by up to 1.5%) than in our 500 ppm No MICI runs. However, the channel pressures are still within 95% of ice overburden, as in present-day Antarctic channels. This suggests that the effect of channels on ice-bed coupling in our paleo simulations is independent of the CO₂ concentration. However, two-way coupled simulations of ice dynamics and hydrology are necessary to determine if this is the case. Similar to our 500 ppm simulations, thick and overpressured water sheets form in basal troughs. In the Eocene 280 ppm run, there is a lower proportion of the domain (54.7%) at and above 98% of ice overburden, compared to the 500 ppm run (58.48%). However, in the Mid-Miocene run, the opposite is true – raising the CO₂ concentration lowers the percent of the domain at high pressure, from 49 % in the 500 ppm run to 43.7 % in the 280 ppm run.

The runs in which the ice geometries were influenced by MICI show considerable departures from the No MICI runs. In the MICI runs, grounding line channel densities were higher, channels tended to be shorter, and channel overburden pressures were lower than those in the No MICI runs. For the paleo runs, these results suggest that, in the absence of MICI processes, variability in CO₂ concentrations can substantially affect subglacial drainage networks. This is likely because the steeper surface slopes in the higher-CO₂ run cause steeper hydraulic potential gradients, resulting in longer channels. While MICI also tends to steepen ice surface, and therefore, hydraulic gradients, we do not observe longer channels in the paleo MICI runs compared to the No MICI runs because the grounding line has retreated much farther back in the runs where MICI is included. This pattern is not generalisable for our future simulations. While we do see shorter channels in the maximum ice loss MICI run, the maximum ice gain MICI simulation resulted in a maximum channel length of 308.73 km, more than 60 km longer than that of the corresponding No MICI run, and the longest channel of all the future runs. To investigate this further, we analysed the ratio of hydraulic potential gradients. In the MICI run, the ratio of hydraulic gradients for maximum ice loss to maximum ice gain is much more similar than in the No MICI runs. This is because the much steeper ice surface slopes in the maximum ice gain MICI run result in steeper hydraulic potential gradients. Relative to its respective No MICI simulation, the hydraulic gradients of the maximum ice gain MICI run are up to two times steeper. Therefore, we attribute the longer channels in the maximum ice gain MICI run to its steeper hydraulic gradients. Text S2 further discusses the interplay between ice geometry and hydraulic gradient.

We also found that the differences between total grounding line discharges in the No MICI versus MICI scenario were dependent on the time snapshot. In the paleo simulations, MICI lowered the total volume of grounding line discharge, with the largest decrease observed in the Mid-Miocene run, where discharges were 2.6 times lower in the MICI run compared to the No MICI run. In the future runs, however, incorporating MICI led to increases in channel discharge. While this increase was relatively small for the maximum ice loss run (3 m³s^-1), channel discharges in the maximum ice gain scenario increased nearly three-fold. The total channelised discharge volume in the maximum ice gain run with MICI run was the largest of all simulations considered, amounting to 198 m³s^-1.

Taken together, our results highlight how MICI can substantially influence the drainage system. We motivate future work to build on what we have presented here by using coupled models that allow for evolving subglacial drainage and ice dynamics, as well as the option for MICI to be switched on and off. In doing so, a complete picture of how variations in subglacial drainage influence ice dynamics, and vice versa, will be obtained.

Ice shelf basal melt impacts

Subglacial outflow across Antarctic grounding lines and into sub-ice shelf ocean cavities has been posited to locally enhance ice shelf basal melting by both enhancing turbulence of the near-grounding line water mass and enhancing buoyancy of sub-ice shelf plumes that drive melting^22,37,38. Using an ice shelf basal melt parameterisation that resolves melt driven by ocean circulation and subglacial freshwater outflow (Pelle et al.³⁹; see Methods), we assess the sensitivity of ice shelf melt rates to the modelled paleo, modern, and future subglacial conditions discussed above. Parameterised ice shelf melt enhancements from subglacial freshwater outflow are strong but highly localised (Fig. 4). In the 500 ppm No MICI paleo simulations, the ice shelf melt enhancement at the Eocene-Oligocene Boundary (maximum enhancement of 38.43 ma^-1) has a higher magnitude and is more spatially concentrated than the melt enhancement at the Mid-Miocene (maximum enhancement of 16.23 ma^-1) due to the varying configurations of the subglacial channels draining across the grounding lines. In both paleo experiments, these melt enhancements comprise up to 70% of the total grounding line melt signal adjacent to the discharge channel (Fig. S32).

Fig. 4: Parameterised ice shelf basal melt from simulated grounding line subglacial outflow.

Panels show the melt enhancements at a, f the Eocene–Oligocene Boundary; b, g the Mid-Miocene; c, h, k modern times; d, I, l 2100 CE under maximum amounts of ice gain; and e, j, m 2100 CE under maximum amounts of ice loss. Red and pink boxes in (a–e) denote the bounds of f–j Totten Glacier and k–m Vincennes Bay glaciers, respectively. Grey shading over grounded ice is the associated bed topography, blue-to-purple shading is the simulated channelised subglacial discharge flux, and red shading over floating ice is the parameterised ice shelf melt enhancement. The grounding line is overlaid onto each panel as a black line. Source data are provided as a Source data file.

In modern and future simulations, along Totten Glacier’s southern grounding zone, small changes in the subglacial channel distribution lead to considerable changes in the downstream limit of the ice shelf melt enhancement (5 L’, see Methods), which reaches a maximum distance of 5.83 km, 10.04 km and 17.72 km in the modern, maximum ice gain, and maximum ice loss experiments, respectively. As ice shelf geometry and ocean conditions are consistent across these experiments, differences in the downstream limit of these melt enhancements are solely caused by differences in the configuration of the subglacial channels at the grounding line (i.e. fluxes and channel widths). In the modern, future maximum ice gain, and future maximum ice loss runs, subglacial outflow leads to enhanced ice shelf basal mass loss of 0.65 Gt, 2.23 Gt, and 3.62 Gt over the Totten Ice Shelf, respectively, and 0.21 Gt, 1.07 Gt, and 0.23 Gt over the Vanderford and Adams ice shelves, respectively (total basal mass loss over the Totten and Vanderford/Adams ice shelves in lieu of discharge are 178.44 Gt and 24.80 Gt, respectively). Although the magnitude of these shelf-integrated discharge-driven ice shelf melt enhancements seems inconsequential, these enhancements comprise up to 30% of the total Totten Ice Shelf grounding line melt signal in modern and maximum ice gain and up to 50% in maximum ice loss scenarios. Melt enhancements of Vincennes Bay outlet glaciers exhibit strong sensitivity to the simulated discharge conditions. Melt enhancements in the modern run are minimal due to the small amounts of simulated discharge (Fig. 4k); however, in 2100 (simulations with a more developed subglacial hydrology system) melt enhancements peak at 58.40 ma^-1 and 25.64 ma^-1 near the Vanderford and Adams grounding lines in maximum ice gain and maximum ice loss scenarios, respectively (Fig. 4l, m). We further explore the sensitivity of 2100 CE ice shelf melting of Vincennes Bay outlet glaciers (pink box in Fig. 4d) to subglacial hydrology model inputs of basal water production, ice velocity, and bed topography for the No MICI maximum ice gain runs (Fig. S33). Melt enhancements reach peak values near the southern limit of the Vanderford Ice Shelf and the Adams Ice Shelf in the modern bed topography experiment (Fig. S33a) and modern inputs experiment (Fig. S33c), respectively, owing to the differing distribution of grounding line discharge between these simulations. We note that in a complementary study, Pelle et al.²³ developed a coupled ISSM-GlaDS configuration of ASB and, in projections to 2100, found that subglacial discharge-driven melt enhancements led to earlier onset of retreat of Totten Glacier’s southern grounding zone by ~25 years and continually accelerated retreat of Vanderford Glacier (up to 10 km of additional retreat compared to uncoupled “ISSM-only” simulations). That is, while the magnitude of these discharge melt enhancements is small relative to the background ocean-driven melt signal, their location at deep grounding line points has cascading impacts on the upstream stress regime of entire glacial basins. As such, the highly sensitive nature of the melt enhancements presented here highlights the importance of better constraining subglacial hydrology model inputs and boundary conditions, which will, in turn, improve simulations of past, present, and future ice sheet dynamics.

Discussion

Pressurised subglacial water is known to play an important role in the flow of Antarctic glaciers, including Totten Glacier in the ASB²¹. Our work shows that ice configuration changes since the inception of the Antarctic Ice Sheet 34 million years ago have resulted in reorganisation of ASB’s subglacial drainage system. This suggests that the region’s ice dynamics were likely highly variable in the geologic past, which fed back into subglacial drainage evolution. Furthermore, we demonstrate that the evolution of subglacial drainage exerts a strong influence on the spatial distribution and magnitudes of ice shelf basal melting. When drainage was focused through few subglacial channels, as in at the Eocene-Oligocene Boundary, 34 million years ago, ice shelf basal melt enhancements were high and localised. In contrast, when the ice in ASB had retreated during the Mid-Miocene, 14 million years ago, melt enhancements were widespread but lower in magnitude and constrained to shorter distances from the grounding line. Despite the differing organisation of melt patterns between the two paleo time snapshots, subglacial hydrology in both scenarios comprised up to 70% of the total ice shelf melt signal, representing a 40% increase relative to present day. We also found that the uncertainties in future trajectories of ice geometries in ASB have outsized impacts on the basal hydrological system and the distribution and magnitudes of ice shelf basal melt. Our work complements the work by Pelle et al.²³, who showed that ASB ice flow is sensitive to the pattern of melt enhancement, especially in regions that are grounded below sea level and vulnerable to unstable and irreversible retreat.

Previous research has suggested that past warm periods can serve as a proxy for future climate warming and ice sheet evolution¹³. Our analysis suggests no one-to-one relationship exists in the context of subglacial hydrology and ice shelf basal melting. For instance, we found similarities between the Eocene-Oligocene Boundary (34 million years ago), when there was more ice in the ASB than at present, and the maximum ice loss scenario for 2100 CE. This may be surprising since the two scenarios are at opposite ends of the spectrum. We indicated that these two scenarios resulted in similar volumes of total subglacial discharge exiting at the grounding line. However, concentrating solely on the magnitude neglects the implications of spatial variability. At the Eocene-Oligocene Boundary, three-quarters of the total discharge crossed Totten Glacier’s grounding line. In the 2100 CE maximum ice loss scenario, this partitioning was different, with a little over a third of the total discharge crossing Totten Glacier’s grounding line and a higher-than-present-day proportion of the water crossing the grounding lines of Bond and Vanderford Glaciers. In our sensitivity tests, ice geometry is crucial in determining the pathways and outlets for subglacial water. Our results confirmed earlier research⁴⁰ highlighting that, with all else held equal, the spatial change in ice surface geometry exerts a dominant control on the pathways and outlets for subglacial water. Recent work has investigated whether water and ice piracy are possible for the ASB if the region were to experience slight changes in ice geometry⁴¹. The authors found that basal water may be redirected from Totten Glacier towards Vanderford Glacier⁴¹. Our work supports these conclusions, showing that water piracy likely occurred in the past and is possible in the future for the ASB. In particular, our future simulations show that Totten Glacier is a less dominant discharger of subglacial water than at present, and that a larger percentage of basal water is expected to drain across Vanderford Glacier’s grounding line at 2100 CE relative to today.

Geomorphological evidence indicates that the ASB experienced several advance and retreat cycles over the last 34 million years^{11,18,19,20,42,43}. It has been suggested that surface meltwater-rich regimes, such as those found in West Greenland^{44,45,46,47,48}, may be responsible for the dynamic behaviour of the ice sheet margin^18,20,42,43 (see also Text S3). However, constraining the timing, volume, and location of meltwater inputs to the bed remains challenging due to the inherent uncertainties in interpreting the time-integrated paleo record, and these uncertainties translate to difficulties in determining the most appropriate surface water routing scheme in hydrology models. Because of these ambiguities, we performed a simple test in which the surface meltwater from Paxman et al.²⁶ was added directly to the bed without seasonal variability. Channel discharge volumes in this test increased, but the channel locations did not change since surface melt was concentrated near the grounding line, where channels had already formed. If, in the coming centuries, surface meltwater was to access the subglacial drainage network, a more dynamic system reminiscent of the paleo ASB and West Greenland may form, triggering highly variable grounding line positions and ice flow patterns, even in the absence of MICI. We motivate future work to build on what we have shown here by investigating variability in surface meltwater inputs to the bed, as this would provide insights into the stability of the ASB drainage network in the face of perturbations to melt supply.

Large-scale, long-term ice sheet modelling exercises are often run at coarse resolutions and with simplified ice dynamics to make the simulations computationally feasible. As a result, processes such as subglacial hydrology that are known to influence ice dynamics are generally neglected. In the sediment stratigraphy of the ASB’s continental margin, there are repeat signatures of sediment wedges and bedrock channels shaped by subglacial meltwater flows^19,20,43, dating from the Eocene to the Miocene. These features are located beyond the grounding lines of the Paxman et al.²⁶ data (and, hence, our GlaDS domains) and indicate that fluctuations in ASB terminus positions were much larger during both cold and warm climate states than what Paxman et al.’s²⁶ results suggest. These mismatches in grounding line locations, in turn, affect our ability to compare our modelled hydrologic pathways to those preserved in the geologic record. The incongruity between geomorphological data and Paxman et al.’s²⁶ ice sheet geometries may be because the latter did not include a hydrology component and the simulations were run at a relatively coarse resolution (10 km), two factors that could influence the relative role of topographic pinning points on ice sheet retreat and expansion (e.g., Ridge A⁴²; see also Text S3). The absence of subglacial hydrology in Paxman et al.’s²⁶ model could have also affected their computed rates and patterns of subglacial erosion and sediment deposition, with cascading effects on the locations and advance/retreat rates of terminus positions. For example, subglacial meltwater that is continuously routed along the same path could create the above-mentioned bedrock channels under grounded ice. The sediment mobilised by subglacial meltwater could then be deposited further offshore, where it could lead to the formation of topographic pinning points that stabilise grounding line positions and affect ice dynamics. Whereas Paxman et al.²⁶ did not incorporate hydrology, our hydrology model does not resolve erosional and depositional processes, and therefore, we are unable to capture the redistribution of sediment in the system by subglacial meltwater and the resulting geomorphological features. The limitations of both Paxman et al.’s²⁶ and our model highlight an opportunity for future work to incorporate erosion, sedimentation, and hydrology in ice sheet models since the bed is not static but instead evolves in concert with, and feeds back on, the ice sheet and hydrology systems. By accounting for these processes, modelling stands to match paleo records better and produce more tightly constrained projections of ice sheet evolution.

We do, however, find overlap between the inferred warm-based and fast-flowing regions indicated by Aitken et al.⁴² and areas of high velocities and melt production in the Paxman et al.²⁶ data that contribute to the high channel discharges in our subglacial hydrology simulations. Isostatic adjustment may also influence long-term hydrology routing, but since we do not couple our subglacial hydrology model to a solid earth model and perform long-term, continuous simulations, the direction or magnitude of potential feedbacks between solid earth effects and hydraulic gradients are unknown. A first step towards testing the suite of interactions could be with fully-coupled, high-resolution studies of areas such as the ASB so that computational expenses are minimised by focussing on one area while resolving the high degree of detail in basal topography and subglacial drainage that is known to exist in the region^{11,18,19,20,21,23,42,43}.

In general, our sensitivity tests indicated that high volumes of basal meltwater may contribute to longer, larger subglacial channels and the extent of high water pressure. Constraining the quantity of water feeding these subglacial drainage pathways is essential for hindcasting and forecasting subglacial drainage development and ice dynamic changes. Since subglacial meltwater affects basal lubrication and sliding speeds⁴⁹, the higher meltwater production rates in the past and future simulations suggest knock-on effects on ice dynamics. Elevated basal meltwater production rates upglacier would result in higher water pressures, implying that faster ice motion could migrate to regions that are currently flowing relatively slowly. At the grounding line, where the ice goes afloat, high volumes of subglacial discharge would cause vigorous ocean mixing and enhancements of ice shelf basal melting, weakening the braking effect that ice shelves provide on the inland ice. Although our hydrology model was not coupled to ice and ocean models, our results shed light on the effects of large-scale drainage reorganisation and the consequences of neglecting evolving subglacial hydrology in ice sheet models. If high water pressure were to move upglacier and higher grounding line channel discharges were to weaken ice shelf buttressing, subglacial water alone could drive sea level contributions from Antarctica that are larger than previously suggested, without the need for instability mechanisms such as MICI. While we have shown that channelised discharge can locally account for up to 70% of total ice shelf melt, it is unknown how the number and spatial distribution of channels across the grounding line influence ice dynamics. It is possible that a limited number of channels with high discharges and focused over a small length of the grounding line could have the same impacts on the (de) stabilisation of ice dynamics as a scenario where many smaller channels occupy the entire grounding line, with changes to the bed and sediment redistribution being a potentially important feedback. Determining the nature of these relationships requires coupling between the ice sheet, the ocean, subglacial sediments, and the subglacial drainage system, and will provide crucial information for assessing past, contemporary, and future sea level contributions. Our work illustrates how past and future ice geometric changes can influence 2-D subglacial drainage and ice shelf melting, and we encourage future modelling efforts to build upon the work presented here by coupling evolving subglacial hydrology, ice shelf melting, and ice dynamics. In doing so, a more comprehensive understanding of the ice dynamic-subglacial hydrology interactions will be obtained.

Methods

Subglacial hydrology modelling

For our subglacial hydrology simulations, we use the Glacier Drainage System (GlaDS) model²⁴. GlaDS is a 2D finite-element model that allows for the co-evolution of distributed and channelised drainage over grounded ice. Distributed drainage is approximated as linked cavities that form on elements of a triangular mesh, which exchange water along element edges where channels form. Rather than being specified at the beginning of the run, these channels develop over the simulation time as fluxes and pressures evolve in the distributed system. The equation describing channel evolution is given by:

$$\frac{\partial S}{\partial t}=\,\frac{\Xi -\Pi }{{\rho }_{i}L}-{AS}{\left|N\right|}^{n-1}N$$

(1)

where $S$ is the channel cross-sectional area, $\Xi$ is the viscous dissipation of potential energy, $\Pi$ describes the sensible heat changes due to changes in pressure melting point, ${\rho }_{i}$ is the ice density, $L$ is the latent heat of fusion, $N$ is the effective pressure within the channel. $A$ and $n$ empirically-derived constants, with the former relating to ice temperature, and the latter to and strain rate.

Although channels can form on any element edge within the domain, we restrict our analysis to channels with discharges >0.5 m³s^-1. To prevent model instabilities, we limit the maximum channel cross-sectional area to 500 m². Close correspondence between GlaDS outputs (e.g., channel outlet locations and ponded water) and remotely sensed present-day basal conditions in East and West Antarctica suggests that the model is ideal for our investigation of paleo and future subglacial hydrology^21,50,51,52.

We constructed 13 domains, one for each of the ice sheet configurations (8 for the paleo simulations, 1 for the present-day simulation, and 4 for the future simulations) considered in our study. These domains were determined by assuming that the subglacial water pressure is equal to ice overburden pressure. Since hydraulic potential analysis is based on the geometry of the ice and bed, the source data in this calculation influence the flow routing and, therefore, the domain size. From here, we construct our meshes, which are restricted to ~20,000 nodes due to computational limitations. We do not have refined regions in the meshes. In Table S1, we summarise key characteristics of the domains and the boundary conditions (e.g., the number of nodes, mesh edge lengths, maximum ice surface and bed elevation, basal water input rates, and basal velocities). We run the model up to steady-state over 30,000 days. Steady state is reached when the distributed water sheet thickness differs by <10^-7 mday^-1 between two consecutive timesteps^21,50,53. After reaching steady state, we run the model for another 10,000 days. Results in the main text show the model outputs at the end of these 10,000 days. At this point, the sheet thickness differences between the two final timesteps range from 2.2 × 10^-8 mday^-1 to 8.52 × 10^-7 mday^-1 and are therefore within our criterion for reaching steady state.

GlaDS requires ice surface and basal topography, basal meltwater production rates (due to geothermal and frictional heating) and basal velocities as inputs. These data come from Paxman et al.²⁶ for the paleo simulations, BedMachine Antarctica¹ and initMIP-Antarctica²⁵ for present day, and Li et al.³⁵ for the future runs. We have summarised the range of values for these inputs in Table S1.

As mentioned in the main text, we selected paleo time snapshots when ice configurations in the ASB were larger (Eocene-Oligocene Boundary) and smaller (Mid-Miocene) than present day. These data are from Paxman et al.²⁶, who explored the sensitivity of Antarctic Ice Sheet evolution to climate changes. Their experiments forced an ice sheet model with CO₂ concentrations of either 280 ppm or 500 ppm, allowing MICI to be turned on or off. Using the Paxman et al. ice sheet model outputs as inputs to the GlaDS model, we consider all possible combinations for each time snapshot: 280 ppm without MICI, 280 ppm with MICI, 500 ppm without MICI, and 500 ppm with MICI. This resulted in a total of 8 simulations (4 for the Eocene-Oligocene Boundary, and 4 for the Mid-Miocene). Li et al.³⁵ forced their ice sheet model with the 36 CMIP6 models available at the time of their publication. Since guidelines for selecting CMIP6 models for ice sheet modelling and analysis were unavailable at the time of writing, we select a subset of the model outputs from Li et al.³⁵ based on a regional analysis of their performance over the ASB. Grounding line retreat distance was not an informative metric since the models showed the same grounding line locations for 2100, likely due to the coarse resolution of the grids that do not capture well basin-scale grounding line migration. Despite these similar grounding line locations, the patterns of ice loss and gain varied greatly between models. We, therefore, use the metric of total ice thickness difference at 2100 relative to 2020 over the ASB for the No MICI simulations. NorESM2-MM resulted in the largest ice loss, while CMCC-CM2-SR5 resulted in the greatest ice thickness gain over the ASB. These models therefore represent the endmembers for ice geometry change over the ASB based on Li et al.’s³⁵ outputs. We also use the MICI complement of this subset of Li et al.³⁵ model outputs, for a total of 4 future model runs.

The results presented in the main manuscript adopt the GlaDS parameter values that resulted in the closest agreement between present day hydrological modelling and remotely-sensed observations in the ASB²¹. These values are summarised in Table S2 in the supplement. In the Supplementary Material, we include the results of our sensitivity tests (Figs. S22–23 and Text S1). We focused on basal meltwater production rates, basal velocity, and basal topography. We ran simulations where we set the basal topography to that of BedMachine Antarctica¹, but use the ice surface geometry, basal velocity, and basal melt data from the source publication. Since, in this test, we are only changing the bed topography but keeping everything else the same as in the source publication, it allows us to determine the level of control that basal topography has on the subglacial drainage system. Although the ice surface slope is known to exert a dominant influence on large-scale subglacial drainage⁴⁰, water flow paths are also sensitive to basal topography^54,55,56, with rerouting and water piracy possible under slight variations in bed topography^54,55,56. Furthermore, large changes in bed slopes over relatively short distances can cause freeze-on as basal water moves from a region of high to low pressure; this effect has been incorporated in GlaDS⁵⁷. Thus, our bed topography test allows us to examine the persistence and sensitivity of subglacial drainage pathways to bed geometry. Our second sensitivity test imposes modern-day values for basal topography, basal velocity and basal meltwater production to all model runs while keeping the ice surface geometry the same as in the source publication. This allows us to assess the role of ice surface topography on the drainage system evolution. Our final test examines the role of meltwater production rates by increasing the modern-day initMIP²⁵ basal water production rates by a factor of 1.5, while keeping the basal velocities and ice and basal geometries the same as in the source publication. This provides an approximation of how melt could vary for ice sheet geometries governed by different ice sheet model physics.

Ice shelf basal melt parameterisation

For each subglacial hydrology simulation, we compute melting driven by sub-ice shelf ocean circulation and grounding line subglacial discharge with the buoyant plume parameterisation developed by Pelle et al.³⁹. This parameterisation, based on the theory of buoyant sub-ice shelf plumes, applies a meltwater plume model⁵⁸ that is modified near grounding line subglacial outflow locations to account for discharge-enhanced ice shelf melt using a discharge plume model³⁷. The meltwater plume model simulates plumes that originate at the grounding line and travel upward along the base of the ice shelf, inducing melt up to the ice front or to the point at which the current loses buoyancy. The plume’s trajectory is controlled primarily by the ambient ocean temperature and salinity (${T}_{a}$ and ${S}_{a}$, respectively), the local slope angle of the ice shelf draft ($\alpha$), and the depth the plume originated that reaches a particular shelf point (grounding line depth, ${z}_{{gl}}$). Within a prescribed distance away from grounding line subglacial discharge locations, melt rates additionally become proportional to the grounding line subglacial freshwater flux (${q}_{{sg}}$) to the one-third power^37,59. This distance (5 L’, metres) that sets the cutoff between the meltwater and discharge plume models is set as a radius around grounding line discharge locations and is governed by the following equation:

$$5{L}^{{\prime} }=\,\frac{500 \cdot {q}_{{sg}}^{\frac{2}{3}}}{{\left(g\cdot \Delta {\rho }_{i}\right)}^{\frac{1}{3}} \cdot {C}_{d}^{\frac{1}{2}}{\varGamma }_{T{s}_{0}}{ \cdot G}_{1}\cdot {G}_{2}^{\frac{1}{3}}\cdot \left({\lambda }_{3}\cdot \Delta {T}_{f,{gl}}\right)}$$

(2)

where ${q}_{{sg}}^{2/3}$ is the grounding line subglacial discharge flux (m²s^-1), $g$ is Earth’s gravitational constant (9.80 ms^-2), $\Delta {\rho }_{i}$ is the density contrast between the plume and ambient ocean waters, ${C}_{d}^{1/2}{\varGamma }_{T{s}_{0}}$ is a heat exchange parameter ($6\cdot {10}^{-4}$), ${G}_{1}$ and ${G}_{2}$ and geometric terms that provide melt rates the proper scaling to the slope angle of the ice shelf draft and grounding line depth field, and ${\lambda }_{3}\cdot \Delta {T}_{f,{gl}}$ is a measure of the ocean thermal forcing (°C). Given inputs of ${T}_{a}$, ${S}_{a}$, $\alpha$, ${z}_{{gl}}$, and ${q}_{{sg}}$, the melt rate parameterisation outputs an ice shelf basal melt rate field that resolves melting driven by both large-scale ocean circulation and localised subglacial discharge. Note that melt enhancements from subglacial discharge were computed by differencing melt fields that were computed with ${q}_{{sg}}$ taken from GlaDS and with ${q}_{{sg}}$ set to zero.

Input ice shelf geometries (providing $\alpha$ and ${z}_{{gl}}$) for both paleo, modern, and future subglacial hydrology simulations are consistent with the descriptions in the above subglacial hydrology modelling methods section. Input ocean conditions (T_a = -0.73 °C, S_a = 34.73 units on the practical salinity scale) for the 280 ppm paleo, modern, and future simulations were obtained by averaging observed⁶⁰ bottom ocean temperature and salinity along the Sabrina Coast. For the 500 ppm paleo simulations, we apply 5 °C ocean warming to remain consistent with Paxman et al.²⁶ and do not change the salinity (i.e., T_a = 4.27 °C and S_a = 34.73 units on the practical salinity scale).