A machine learning model for hub-height short-term wind speed prediction

Abstract

Accurate short-term wind speed prediction is crucial for maintaining the safe, stable, and efficient operation of wind power systems. We propose a multivariate meteorological data fusion wind prediction network (MFWPN) to study fine-grid vector wind speed prediction, taking Northeast China as an example. Results show that MFWPN outperforms the ECMWF-HRES model regarding vector wind speed prediction accuracy within the first 6 h. Transfer experiments demonstrate the good generalized performance of the MFWPN, which can be quickly applied to offsite prediction. Efficiency experiments show that the MFWPN takes only 18 ms to predict vector wind speeds on a 24-hour fine grid over the future northeastern region. With its demonstrated accuracy and efficiency, the MFWPN can be an effective tool for predicting vector wind speeds in large regional wind centers and can help in ultrashort- and short-term deployment planning for wind power.

Introduction

The changing world climate has encouraged societies to look for alternative clean energy sources to fossil fuels. As an inexhaustible clean energy source, wind energy is crucial in the future energy mix^1,2. However, the stochastic nature of wind power and its inability to be stored also lead to uncertainties in wind power supply. In addition, the strong stochasticity and volatility of wind speed also present significant challenges to the safe and stable operation of wind farms³. Relying solely on real-time wind speed data limits the responsiveness of a control system, reduces power utilization, and leads to an unstable wind power supply. In the context of large-scale integration of wind power into a grid system, this instability can reduce economic benefits and even cause “wind abandonment“⁴. Therefore, accurate short-term wind speed prediction (WSP) is essential for the guidance, scheduling, operation, and maintenance of wind power⁵.

China has abundant wind and solar resources, and their energy potential is sufficient to meet 1.5 times China’s expected electricity demand in 2050⁶. To fully utilize wind resources and accomplish the goals of peak carbon dioxide and carbon neutrality, China is vigorously developing its wind power industry. As one of the wealthiest regions in China in terms of wind energy resources, Northeast China will be densely distributed with wind turbines in the future. Therefore, to respond to future demands for predicting wind power generation over a wide area, this study focuses on refined-grid WSP in Northeast China to help wind power centers (WPCs) schedule and operate wind power networks in a large region. Existing wind speed prediction systems include ultrashort, short-time⁷, and long-time prediction systems⁸. Ultra-short time is generally a minute-level forecast, predicting wind speeds for the next 10 min^9,10 and 1 h¹¹. Short-term wind forecasts are generally hourly, from 1 to 6 h^12,13,14 and even 24 h^15,16. Our short-term wind speed prediction research plans to achieve high accuracy wind speed prediction for up to 6 h and wind speed trend prediction for up to 24 h with a temporal resolution of 1 h. Regional fine-grid WSP can be formulated as a space‒time series prediction problem: given a time-varying historical spatial and temporal distribution of wind speed, the spatial and temporal distributions of wind speed within a specific time range can be predicted in the future. Accurate and efficient WSP is a complex problem because the evolution of wind speed involves the coupling of space, time, and multiple meteorological factors. The main challenges of WSP are as follows:

The role of different meteorological factors on wind speed: Many wind speed prediction methods only study the evolution of wind speed itself^15,17,18, ignoring other meteorological factors that are closely related to wind, such as geopotential, temperature, and elevation. The formation of wind results from the synergistic effects of various meteorological factors in nature. Ideally, temperature differences create pressure differences, which lead to pressure gradient forces that form winds. Both the wind speed and direction are altered by topography. Considering only the vector wind speed information obtained by wind speed sensors and ignoring information from temperature sensors and pressure sensors limits the improvement of WSP accuracy.

Global temporal dependence of wind speed series: Determining the global temporal dependence of wind speed series plays a crucial role in accurate WSP. However, existing studies have usually focused on the temporal dependence of neighboring wind speed sequences^19,20. On the one hand, uncertainty severely affects the prediction accuracy as the prediction period is extended. On the other hand, the inherent dynamic variability of wind speed series further increases the uncertainty of WSP. Therefore, it is essential to determine the global dependence of wind speed series.

Dynamic spatial dependence of wind speed: The spatial distribution of wind speed is a whole with spatial solid linkages. Many previous works have ignored spatial connections¹⁷, considered spatial dependence solely in a static way²¹, or used a dynamic graph network to model the spatial dependence of a finite number of observations. Convolution helps capture the dynamic spatial connections among wind speed sequences. However, the local “feel-good” field property of convolution cannot capture global spatial dependence. Therefore, fully capturing the dynamic spatial dependencies of wind speed data is difficult.

Currently, WSP can be divided into two main methods: one based on physical models and the other on data-driven methods^22,23. Numerical model-based approaches are standard physical methods for modeling weather via complex thermodynamic and hydrodynamic equations. They describe the evolution of weather by solving many differential equations on the basis of a given initial value^24,25. Numerical models integrate relevant meteorological factors, including temperature, pressure, geopotential, density, humidity, and terrain, to predict detectable wind speed. Classic numerical models include Weather Research and Forecasting, Integrated Forecasting Systems, and European Center for Medium-Range Weather Forecasts. Although these numerical models provide better results in mesoscale and large-scale prediction, they require many computational, storage, and temporal resources^26,27. In addition, it is challenging to meet the accuracy and timeliness requirements necessary for short-term forecasting, which limits the application of numerical models for WSP²⁸.

Data-driven methods, which learn historical wind speed evolution patterns and then project the wind speed in the future, mainly include statistical and machine learning methods. The autoregressive integrated moving average model (ARIMA) family of statistical models is the classic time series forecasting method. Autoregressive models use the previous values of a time series to predict future values²⁹. ARMA combines regression modeling and moving averages to describe and forecast time series models on the basis of their own past values and past errors^30,31. The ARIMA model adds a differencing process to ARMA to transform a nonstationary time series into a stationary one^32,33. Singh et al. combined the wavelet transform with the ARIMA model, achieving good results in short-term WSP¹⁸. Hill et al. utilized ARIMA and detrending techniques to predict wind speed²⁹. When faced with more straightforward, small amounts of wind speed data, statistical methods can identify geopotential features of wind speed evolution well enough to predict future wind speeds. However, when the amount of data increases, the number of prediction steps increases, and the wind speed strongly fluctuates, as shown in Supplementary Fig. 1 and Supplementary Fig. 2. These models have difficulty capturing the complex nonlinear features of the wind, and the prediction error increases dramatically³⁴. With the successful application of machine learning methods in various fields, several machine learning algorithms, including SVM^35,36, artificial neural network³⁷, and support vector regression³⁸, have also been introduced to predict future wind speed. Kramer et al. used a support vector regression framework for wind prediction within six hours³⁸. Hu et al. derived an optimal loss function for heteroskedastic regression and proposed a SVR short-term wind prediction framework on the basis of the heteroskedastic Gaussian noise learning task³⁹. Tian et al. decomposed a short-term wind speed time series via local mean decomposition and then used a combined kernel function least squares SVM for prediction⁴⁰. The choice of hyperparameters is essential for classic machine learning algorithms, but it is laborious. Li et al. improved the dragonfly algorithm to obtain the optimal parameters for a support vector machine³⁶. Classic machine learning algorithms can quickly achieve accurate results for small-scale wind field prediction. However, when facing the demand for WSP at large scales, such as in Northeast China, complex spatiotemporal evolution requires a more powerful nonlinear feature extraction capability, which could require by shallow machine learning models^8,15.

Deep learning has attracted the attention of many scholars in WSP due to its powerful fitting ability⁷. Compared with classic machine learning methods, deep learning methods have deeper networks and can fit more complex nonlinear relationships. The long short-term memory network (LSTM)⁴¹ is a classic deep-learning temporal prediction model that extracts temporal dependencies by designing memory and forgetting gates. Li et al. proposed a short-term wind speed interval prediction method that combines a gated recurrent unit⁴² and variational mode decomposition. Farah et al. proposed a short-term WSP method that combines data decomposition and bidirectional LSTM¹⁹. U et al. used gated recurrent units and LSTM to predict future wind power at 1-h, 3-h, 5-h and 12-h intervals²⁰. Several studies have incorporated additional meteorological variables, such as temperature, barometric pressure, and humidity, to enhance wind speed prediction^43,44,45. Shang et al. proposed an integrated wind speed prediction system using a self-organizing map to cluster meteorological factors and a regularized limit learning machine to predict wind speed⁴⁴. Wei et al. extracted wind speed and other meteorological variable features using autoencoder and singular value decomposition, after which a GRU was used to predict wind speed time series⁴⁶. These WSP methods predict the wind speed time series data for a specific observation point without considering the connection with other observation points. However, because wind is a fluid, it is strongly spatially correlated, as shown in Supplementary Fig. 1. Limiting the wind speed to the current observation point and abandoning other spatial data might hinder the improvement of prediction accuracy^13,15. Moreover, with the widespread popularity of wind power, the macro control of WPCs requires a regional WSP model to guarantee the safe and stable operation of a power grid instead of spending considerable resources to monitor each wind point.

Numerous studies on spatiotemporal wind speed prediction have leveraged ConvLSTM⁴⁷, integrating convolutional and recurrent neural network models to capture the spatiotemporal dynamics of the wind field. Zhu and Chen et al. investigated the potential of combining convolutional neural networks (CNNs) and recurrent neural networks (RNNs) to generate a spatiotemporal correlation representation of WSP^48,49. Yang et al. proposed the deep attention convolutional recurrent model based on K-shape and enhanced memory, which integrates an attention layer, CNN, and RNN to extract a spatiotemporal potential representation and improve WSP performance⁵⁰. An undirected graph¹³ between observation points was built via a graph neural network to capture robust spatiotemporal wind speed and direction features at multiple neighboring wind measurement sites. LSTM pairs were subsequently used to extract the temporal features of the wind speed at each site. Graphcast extracts spatiotemporal-dependent features of meteorological variables by modeling the Earth’s surface as a graph structure and performs well in short- and medium-term weather prediction⁵¹. The STDGN introduced the self-attention separation method to integrate spatial, temporal, and variational data for multivariate weather prediction⁵². However, self-attention is strong for global dependency extraction and weak for local feature extraction. Gao et al. proposed a spatiotemporal multi-wave network based on three-dimensional convolution, which utilizes a wavelet module, multi-scale embedding, and temporal information fusion module to synthesize the temperature barometric pressure and wind speed, and predicts multivariate meteorological distributions in several regions⁵³. Lin et al. utilized attention and convolution to enhance wind feature extraction to predict offshore wind speed⁵⁴. Generally, the errors of an imperfect wind speed prediction model can be classified into two categories: 1) systematic errors, which arise from the model’s inability to adequately model the deterministic evolution of the winds, and 2) uncertainty errors, which arise from the stochasticity and uncertainty of the winds themselves⁵⁵. Although some methods have integrated multivariate meteorological variables to mitigate uncertainty, most current fusion approaches employ multi-task forecasting, which makes it challenging to centrally capture the key dynamics driving wind speed changes. Moreover, the nonlinear features of wind speed may be masked by the changing patterns of smooth variables.

In this work, we propose a method for refined grid vector wind speed prediction, namely, a multivariate spatiotemporal fusion wind prediction network (MFWPN). This method addresses the need for deterministic modeling of wind speed by a CNN-Transformer-based spatiotemporal feature evolution module, including spatial feature encoder-decoder and temporal units. To capture the uncertain evolution of the wind, we design a spatial fusion module and a temporal fusion module, which employs an LSTM-like gating mechanism to extract precursory knowledge of the winds from the evolution of topography, geopotential, and temperature. Finally, a composite loss function that mixes structure, velocity, and wind direction is designed for the model to better fit the spatiotemporal distribution of wind. More details about the MFWPN model architecture are available in “Methods”. The results demonstrate that MFWPN outperforms the ECMWF-HRES model regarding wind speed prediction accuracy within the first 6 h. After fine-tuning, MFWPN can be applied to various climatic regions, and its inference speed surpasses that of both ECMWF-HRES and other machine learning models, making it highly efficient for practical applications. Therefore, MFWPN presents itself as a valuable tool for wind power centers, enabling accurate regional wind speed forecasts and facilitating the overall management of regional wind power.

Results

Implementation details

All the experiments are conducted on the same equipment, and the relevant parameters are shown in Supplementary Table 1. In the MFWPN training procedure, the initial learning rate is 0.001, and the optimization is done using Adam. The comparison methods include CNN⁵⁶, ConvLSTM⁴⁷, E3DLSTM⁵⁵, PhyDNet⁵⁷, SimVP⁵⁸, TAU⁵⁹, STDGN⁵², WPN and ECMWF-HRES. Among them, CNN and ConvLSTM are classical spatiotemporal prediction algorithms. E3DLSTM, PhyDNet, SimVP, and TAU are the current prediction algorithms of SOTA, which are widely used in classical spatiotemporal domains, such as meteorological prediction. The parameters for all machine learning models are provided in Supplementary Table 2. WPN is the model in which MFWPN has not fused the information of other variables. The hyperparameters of the comparison models were trained and fine-tuned based on their respective open-source engineering until the best results emerged. All machine learning models are trained on the same dataset with a training batch size of 4 and 100 Epochs. ECMWF-HRES (European Center for Medium-Range Weather Forecasts - High Resolution) is one of the most accurate numerical weather prediction models in the world^60,61, and it is widely used in global meteorological research and weather forecasting by its high resolution, advanced data assimilation techniques, and excellent forecasting performance.

Comprehensive performance analysis

Tables 1, 2, and 3 present the evaluation results of each algorithm in terms of the RMSE, MAE, and ACC, respectively. All models predict wind speeds twice a day, each time for the next 24 h. Comparative results for each machine learning model predicting four times a day are presented in Supplementary Table 3, Supplementary Table 4 and Supplementary Table 5. The MAE shows each model’s basic prediction of the wind speed distribution, the RMSE is better able to show each model’s prediction effect on the wind speed fluctuation, and the ACC reflects the difference between the real wind field evolution pattern and the obtained prediction. Owing to the inability to extract temporal relationships, CNN can utilize only the spatial connection of the current wind speed distribution to infer the wind speed distribution within a concise step. For example, the RMSE of the first step prediction reaches 0.64 m s⁻¹. With increasing time, the prediction effect of convolution rapidly decreases. ConvLSTM and E3DLSTM combine convolution and LSTM and can capture the spatiotemporal evolution of the wind field. However, the LSTM-like network cannot stack multiple layers to optimize long-time feature extraction because of the defect of gradient propagation, so the prediction effect is not good with the extension of time. Both SimVP and TAU are fully convolutional networks, which greatly improve the efficiency of the spatiotemporal prediction problem. However, the accuracy of the WSP is also limited because of the insufficient spatial and temporal feature extraction capability. STDGN is a self-attention method that relies on attention to tap into the relationships among space, time, and channels. Its results are also stronger than those of classic spatiotemporal prediction methods. PhyDNet uses deep networks to construct physically constrained models, but the experimental results demonstrate that it is not applicable to complex WSP. The above methods are designed to reduce the systematic errors caused by the deterministic evolution of the spatiotemporal sequence of wind speeds. As shown in Tables 1, 2, and 3, without considering multivariate data, WPN still achieves good prediction results, outperforming the classic spatiotemporal prediction algorithm and other SOTA models. This may be attributed to the fact that the spatiotemporal feature extractor of the WPN can better model the deterministic evolution process of the wind speed spatiotemporal sequence. The spatial feature extractor consisting of convolution attention can extract sufficient spatial dependencies of the wind speed, and the temporal unit enables the model to extract inter- and multiframe temporal dependencies, which can efficiently reduce the deterministic prediction error of the wind speed. In multivariate fusion, the precursory knowledge of wind speed evolution is extracted from the spatial and temporal evolution of temperature and geopotential via LSTM-style spatiotemporal fusion to help the model learn the uncertainty of the long-term WSP, significantly improving the accuracy of the WSP. In the prediction with a 1-hour lead time, the RMSE is 1.22 m s⁻¹ for ECMWF and 0.42 m s⁻¹ for MFWPN, which is a 66% difference. At a lead time of 6 h, the predicted RMSE of MFWPN is slightly weaker than that of ECMWF, but the ACC is higher than it. However, with the extension of time, the prediction effect of MFWPN decreases faster than that of ECMWF, suggesting that the ability of ECMWF to capture the climate evolution pattern in long-term forecasts is more robust. Comparison with large numerical models shows that MFWPN has better performance in wind speed forecasting for wind farms within 6 h. Together with the higher efficiency of the machine learning model, this provides confidence in the application of MFWPN in wind power.

Table 1 RMSE results of different models for WSP

Table 2 MAE results of different models for WSP

Table 3 ACC results of different models for WSP

Keeping the wind turbine oriented in the optimal direction while operating maximizes wind energy capture, improves power generation efficiency, and reduces mechanical stress to protect the mechanical devices of the wind turbine. The wind turbine receives data from the wind direction sensor. The yaw control system analyzes these data and adjusts the orientation of the wind turbine. The MFWPN can help the yaw control system predict the future wind direction and make more timely adjustments. Table 4 shows the accuracy of each algorithm in terms of wind direction prediction. For the 0-h prediction, machine learning models achieve perfect results, with $WDFA$ reaching over 98% at 90 degrees and over 93% at 22.5 degrees. However, the ECMWF’s short-term forecasting results are not so good. The ECMWF’s $WDF{A}_{22.5}$ at the first hour trails MFWPN by 33.48%, which reflects its poor short-term prediction ability. It is challenging to meet the demand for wind farms that value timeliness, such as performance in short-term prediction. For the 3-h prediction, the MFWPN’s $WDF{A}_{22.5}$ remains above 85%, outperforming the other models. With the extension of time, MFWPN still has the highest $WDF{A}_{22.5}$. The data chosen for this study are vector wind speeds consisting of u-wind and v-wind, so wind direction prediction also demonstrates the robustness of the network to multichannel prediction. The higher the wind prediction accuracy is, the more robust the channel robustness of our proposed network. The performance of the MFWPN in wind prediction demonstrates that it can provide reliable short-term wind prediction for yawing systems, helping turbines improve their power generation efficiency and guaranteeing the safety of turbines under high wind speed conditions.

Table 4 $WDFA$ results of different models for WSP

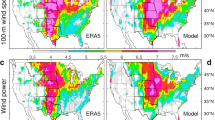
To visually compare each algorithm’s performance, we evaluate each model’s prediction effect for the whole year of 2023 by predicting twice a day. Figure 1 visualizes these results. In the two 12-h forecasts before and after, the machine learning model’s prediction longitude decreases significantly with the extension of time, and the ECMWF model is more robust in the prediction. MFWPN achieves better results than other machine learning models regarding prediction accuracy. Compared to the ECMWF model, MFWPN has a specific lead in the prediction effect in the earlier period, especially in the latter 12-h period. However, with faster inference and inexpensive consumption, MFWPN can achieve more projections more times a day. We placed the predictions of MFWPN−6 (4 predictions in a day, 6 h at a time) and can see that MFWPN outperforms ECMWF overall. However, MFWPN requires a complete set of input variables, including wind speed, temperature, and geopotential. Currently, the data is sourced from ERA5, a reanalysis dataset generated through the assimilation of observational data and inference by the Integrated Forecasting System. This reliance on reanalysis data presents a limitation for fast forecasting models with 6-h intervals. However, as wind turbines become more densely distributed, they will be equipped with sensors such as anemometers, barometers, and thermometers. This will make it increasingly feasible to obtain real-time multivariate data, including wind speed, temperature, and barometric pressure. Such data will significantly enhance the applicability of machine learning models, particularly for wind speed prediction over short time scales.

Fig. 1: Comparison of the next 24 h of WSP by each algorithm.

a is RMSE result. b is MAE result. c is ACC result. For a fair comparison with the ECMWF numerical model, the machine learning 24-hprediction model is used here to predict twice a day, each time taking the results of the first 12 h. MFWPN−6 denotes that the MFWPN 24-h prediction model predicts four times a day, each taking the results of the first six h of the prediction. The breaks on the horizontal axis indicate the intervals where the predictions are made twice a day. These figures shows that MFWPN outperforms ECMWF in the first 6 h of wind prediction.

To demonstrate the model’s ability to capture spatial and temporal features, we visualize the prediction results of MFWPN−6. The summer months are selected as July, August, and September, and the winter months are selected as December, January, and February. Figure 2 visualizes these results. Northeast China is influenced by Daxinganling and Zhangguangcailing, and the narrow tube effect shapes the northeast windy region. In the ERA5 visualization, the distribution of wind speeds in winter and summer reflects the rich wind resources in the Northeast region. There is a clear boundary between the wind speeds in the land and sea areas, and the ocean area has higher wind speeds. In the spatial distribution of wind speed, the prediction result of MFWPN is not much different from the truth, which proves that the model can capture this overall spatial distribution. MFWPN performs better in winter than in summer, which may be because the meteorological conditions in summer are more complicated. With the extension of the prediction time, the wind speed prediction in some fluctuating regions worsens, but the overall difference is insignificant. The Siberian high pressure in winter brings mainly northwesterly winds to northeast China. The ERA5 in Fig. 3 shows that the wind direction in the local area is northwesterly. However, it may now be due to the pooling of southwesterly winds formed in the southern region under the influence of the stronger southwesterly sea-land winds formed offshore. A comparison of the ERA5 and MFWPN shows that MFWPN has successfully captured this meteorological pattern, and the wind speed and direction distribution predictions are accurate. The summer Pacific high pressure brings strong southerly winds to the Northeast, and a comparison of the distribution of predicted and actual values at this time shows that MFWPN’s predictions are also accurate.

Fig. 2: Visualization of the WSP results for Northeast China.

The first two rows indicate the 2023 winter mean wind speed, and the following two rows indicate the 2023 summer mean wind speed. True and Predicted denote the ERA5 wind speed and the MFWPN predicted wind speed, respectively. From left to right, the wind speeds are shown for the 1st hour, 3rd hour, and 6th hour. The legend on the right shows that the average wind speeds in the Northeast are higher in the winter than in the summer.

Fig. 3: Wind speed and direction for the key region.

The region is labeled red in Fig. 2, the direction of the black arrow indicates the direction of the wind, and the length of the arrow indicates the wind speed. The wind speed results for January 2 using the January 1 forecast are shown for winter, and the forecast results for August 2 are shown for summer. From the comparison, MFWPN can realize accurate vector wind speed prediction for the key area at this time point.

Vector wind speed analysis in key areas

To demonstrate the WSP capability of the MFWPN in key regions, we selected Harbin and Chifeng, important WPCs in Northeast China, for prediction evaluation. Harbin is in the northeastern plain, in the midlatitude continental monsoon climate zone, with flat terrain in the middle of the gap between Daxinganling and Zhangguangcailing, and is rich in wind resources. Chifeng, which is in the eastern part of the Inner Mongolia Autonomous Region and has high altitude and abundant wind resources, is suitable for large-scale wind farm construction. Figure 4 show the wind rose maps of the Chifeng and Harbin. Comparing the ERA5 real wind rose, ConvLSTM, and MFWPN predicted wind rose, it can be found that the MFWPN model shows a prediction ability closer to the truth in the distribution of the leading wind direction in the two locations. Specifically, the ERA5 wind roses show that the wind direction in Chifeng is more stable, dominated by southeasterly winds, accompanied by a small amount of northwesterly winds. Southwesterly winds dominate the wind direction in Harbin, and MFWPN can accurately capture the distribution of this significant wind direction, which is close to the truth and has a more reasonable coverage in the direction. In contrast, the ConvLSTM model has some deviation in the distribution of the leading wind direction, and the proportion may be overestimated or underestimated, indicating its limited ability to model the main wind direction. In terms of the wind speed intensity distribution, the ERA5 wind roses show that the medium wind speed (6–15 m s⁻¹) occupies a more significant proportion in the two locations, while the proportion of the high wind speed section ( ≥ 18 m s⁻¹) is lower. MFWPN can fit this distribution better and perform more accurately in the medium wind speed section. Overall, MFWPN shows substantial modeling capability and prediction accuracy for the joint distribution of wind direction and wind speed in the key regions.

Fig. 4: Wind roses for 2023 in wind power focus areas.

a is Chifeng. b is Harbin. On the left is the ERA5 wind rose, in the center is the predicted wind rose from ConvLSTM, and on the right is the predicted wind rose from MFWPN. The direction is where the wind is blowing, and different colors indicate different wind speed magnitudes. On the left legend, the wind speed is set up in intervals of 3 m s⁻¹. This figure shows that MFWPN can accurately forecast the wind speeds in the key areas.

Transfer and robust performance

Experiments have demonstrated the accuracy of the MFWPN in predicting wind speed in Northeast China, but transferability and robustness are also two essential indices for practical application algorithms. The transferability of deep neural networks has always been an important issue that cannot be avoided in their application. Training a neural network model is the most time-consuming process in deep learning applications. If the trained model is fine-tuned or can be directly used to predict wind speeds in other regions, it can save significant computational resources and preparation time. Our transferability experiment involves the prediction of wind speeds along the east coast of China and Southeast Asia via a model trained on data from Northeast China. Before forecasting, we used the dataset of the region to be forecasted to fine-tune the 24-h forecasting model for the Northeast region by one epoch. The results are presented using four forecasts a day. Supplementary Table 6 shows the results of the transfer test for the two regions.

Supplementary Table 6 shows that the fine-tuned Northeast model predicts the east coast with ACCs of 0.99 and 0.95 for the first and third hours, respectively, which are almost as good as those of the Northeast model. With respect to the wind direction forecasts, the accuracy of the 6th hour 8-direction for East China remains as high as 90.45%. For the key regional forecast, Yancheng, the coastal WPC, was chosen for the wind rose display. Yancheng’s annual average wind speed at a height of 100 m is more than 7.6 m s⁻¹, and the annual equivalent total load hours can reach 3000–3600 h. Yancheng is one of the best conditions for developing and constructing coastal wind power in China. The ERA5 wind roses in Supplementary Fig. 3 show higher average wind speeds in Yancheng City and an average distribution of multiple wind directions. For this situation, MFWPN can make real-time adjustments to the fan by predicting the wind direction to improve the power generation efficiency of the wind turbine and protect the safety of the wind turbine hardware. For the transfer prediction in Southeast Asia, the fine-tuned Northeast model reached an ACC of 0.99 in the first hour and an ACC of 0.93 in the 6th hour. Regarding to wind direction prediction, the accuracy of the 6th hour 8-direction prediction reaches 92%, which still provides accurate future wind directions for wind turbines. On the one hand, it is easier to predict wind speed with less fluctuation in the vast ocean area of Southeast Asia. On the other hand, Northeast China has a temperate continental climate, and the selected Southeast Asian region has a tropical climate. The transfer results in entirely different climatic regions demonstrate the strong transfer capability of the MFWPN and provide confidence in the flexible application of MFWPN in the later stage.

To further demonstrate the performance of the transfer forecasts, we obtain the mean wind speeds for 2023 in eastern coastal region of China and Southeast Asia to visualize and compare ERA5 and forecast results. Supplementary Fig. 4 shows the prediction results for eastern China and Southeast Asia. In the visualization of ERA5, there is a clear land-sea divide in the wind speed distribution along the eastern coast. The flatness of the ocean is more likely to bring strong wind speeds than the occlusion caused by undulations in the land. Compared with the east coast of China, the land area of Southeast Asia is smaller, and the interaction between land and sea is not obvious enough, so there is no clear interval between the wind speeds of land and sea. Comparing the ERA5 and predicted wind speeds of the two regions, the general consistency reflects the well transfer performance of the MFWPN and its ability to predict complex sea-land mixed wind regions.

The temporal robustness of the MFWPN is evaluated by predicting wind speeds for several different intervals in the future via 24-h historical data. The prediction results of each model are shown in Supplementary Fig. 5. It indicates that the prediction error gradually increases as the prediction time increases. However, the performance is basically the same for all time intervals, which shows the robustness of the model in predicting different time intervals. The shorter-time prediction model achieves higher prediction accuracy, reaching an RMSE of 0.26 m s⁻¹ when predicting only one hour into the future and accuracies of 0.26 m s⁻¹, 0.49 m s⁻¹, and 0.67 m s⁻¹ when predicting only three hours into the future. This gives us the flexibility to use models for different periods when faced with the need to predict for different periods. A comparison of the results of each machine learning model in Fig. 1 shows that although all the models weaken with increasing time, MFWPN stays ahead at every time point. This is because our temporal units and temporal fusion module make MFWPN more time robust.

Efficiency analysis

The inference speed of a model is crucial for its efficiency in real-world applications. To measure the inference speed of MFWPN, we compare it with several other models, and Table 5 shows the experimental results. Without the use of the multivariate fusion module, the GFlops of WPN is 63, which is not advantageous compared with STDGN and PhyDNet, but we note a single 24-h wind speed prediction of 13 ms, which is far ahead of those of the other algorithms. More critically, the WPN inference accuracy is also higher than that of other algorithms. After using the multivariate fusion module, the prediction accuracy of MFWPN achieves a significant improvement but requires more computing power. Happily, the model inference time after fusion does not increase significantly and only increases to 18 ms. When faced with limited computing power, we can use the WPN to forecast the vector wind speed. If the computing power is sufficient, we can use the MFWPN. Regardless of the type of model, it can provide accurate and efficient WSP service.

Table 5 Comparison of the prediction efficiency of the models

Discussion

Accurate and efficient prediction of the vector wind speed is significant for wind power development. In this work, we propose a multivariate data fusion vector wind speed prediction (WSP) network, the MFWPN, to meet the demand of fast WSP frameworks for rapid wind power development. In this work, we propose a multisource data fusion vector WSP network, the MFWPN, to meet the demand of WSP for rapid wind power development. MFWPN predicts the future 24-h wind speeds in northeast China, with the MAE of 0.32 m/s in the first hour and 0.64 m/s in the third hour. For the wind direction prediction, the accuracies for the eight wind directions in the 1st and 4th hours are 99.26% and 95.44%, respectively. MFWPN outperforms the ECMWF model in wind speed prediction within 6 h. The prediction results for Harbin, Chifeng, and Yancheng show that MFWPN can provide accurate wind field forecasts for key areas of the wind energy industry. MFWPN has good transferability and can be well adapted to different WSP scenarios, such as land, sea, and different climatic regions, which can save much time and computational resources by transferring and fine-tuning. It took only 18 ms for MFWPN to complete the WSP for Northeast China for the next 24 h, and its high efficiency lays the foundation for its practical application. In conclusion, the MFWPN performs well in handling short-term WSP, which means that the MFWPN can serve as a valuable tool for wind power facilities to assess grid vector wind speeds.

However, there are still some limitations to this work. The first is the limitation of the data used. The experimental data currently used is from the ERA5 reanalysis dataset, with a spatial resolution of 0.25° × 0.25°, which, while being among the higher resolutions used in meteorological modeling, may not be able to capture wind speed variations at finer scales. At the height layer, currently MFWPN can only support 100-meter height wind speed prediction, and cannot provide multi-level wind speed prediction like the NWP model. In the next stage, we plan to realize multi-level wind speed output by replacing the training data and adjusting the network architecture. The temporal resolution of the dataset is 1 h, which may result in an inability to predict the rapid changes in wind speed associated with extreme weather, such as gusty winds or frontal systems that may occur on shorter time scales. The model must be fine-tuned or re-trained when applied to other regions or scenarios at other resolutions. Although the model uses geopotential, temperature, and wind speed as inputs, these variables may not fully encompass all the physical processes involved in wind speed changes. For example, turbulence, humidity, boundary layer processes, soil moisture, and land cover may significantly impact wind speed but are not directly included. This simplification may lead to errors, especially under complex meteorological conditions such as monsoons, frontal systems, or cyclones. In addition, WSP has a time interval problem. Because of the dataset, we cannot predict the interval wind speed between each time point. Therefore, the MFWPN is more of a guide for the upper WPCs than for the turbines.

In practice, models may struggle to provide reliable predictions during extreme weather events such as typhoons, where nonlinear interactions between atmospheric variables dominate. Additional model calibration or coupling with physically based numerical weather prediction systems may be required in such cases. When applied to more significant regions, MFWPN requires some additional arithmetic power to complete the model training. In our future research, we will continue to develop MFWPN in the direction of multi-source information input, ensemble prediction, and multi-scale modeling to continuously develop the wind speed prediction model’s potential and provide greater assistance to wind power and lower-altitude economic development. As wind power generation has expanded, public concern about energy stability and reliability has also increased. Accurate wind speed forecasts can increase public confidence in wind energy as a sustainable source, making it a more established and competitive energy option. In addition, it is recommended that governments install weather sensors on turbines to obtain wind-related data at wind turbine heights. We call for all governments to share wind data to jointly construct global wind field data at wind turbine heights to facilitate the development of WSP methods and assist in constructing intelligent WPCs.

Methods

Data

Influenced by Asian high pressure in winter and Pacific high pressure in summer, Northeast China has an abundance of wind resources and is vigorously developing the wind power industry. Therefore, in this study, Northeast China, with a latitudinal and longitudinal range of approximately [38°−54°N, 116°−136°E], is selected for the WSP study, as shown in Fig. 5. We used the 100-meter height u-wind and v-wind data from ERA5⁶² for the hub-height wind prediction study. We chose geopotential, temperature, and elevation as auxiliary variables to match the prediction of wind at 100 m height. According to the International Standard Atmosphere, the 100 m height is closer to 1000 hpa, so we choose the geopotential and temperature at 1000 hpa. The spatial resolution of the selected data is 0.25° × 0.25° and the temporal resolution is 1 h. Geopotential measures the geopotential energy of a unit mass at a given height in the Earth’s gravitational field. Differences in geopotential height at a constant pressure level correspond to differences in pressure at a constant altitude. A higher geopotential height at a pressure surface indicates higher pressure below, and vice versa. In synoptic-scale systems, atmospheric pressure and temperature are fundamental determinants of wind speed. Pressure gradients drive large-scale air movement, while temperature influences air density and vertical motion, modulating wind velocity. Near the surface, wind speed becomes more complex due to additional factors such as terrain, surface roughness, and turbulence, which introduce further variability. Nonetheless, pressure and temperature remain essential meteorological variables, as they govern atmospheric stability, air mass interactions, and density distribution, which in turn dictate the fundamental characteristics of wind, including its magnitude and direction.

Fig. 5: Topographic map of the study area.

a is the Northeast China. b is the East coastal region of China. c is the Southeast Asia. The legend at the bottom of the picture indicates the elevation. On a line of longitude, the actual distance is roughly 111 kilometers for every degree difference in latitude. On the line of latitude, for each degree difference in longitude, the actual distance differs by roughly 111 × cosθ kilometers. θ denotes longitude degree. The size of the actual distance in (a) is about 1776 km × 2220 km. Harbin and Chifeng in (a) are important wind power center cities. Chifeng is at a higher elevation. Harbin is at a lower elevation and is in the middle of two mountain ranges. Yancheng City in (b) is a wind power center on the southeast coast of China. In (c), Manila is rich in sea wind resources and has a large offshore wind farm.

To demonstrate the performance of the method proposed in this study, we additionally selected ranges containing the east coastal region of China [115°−123°E, 29°−37°N] and Southeast Asia [116°−132°E, 1°−17°N] for the validation experiments, as shown in Fig. 5.

This study selected a six-year sequence of wind speeds for 2018-2023, using 2018-2022 for training and validation and 2023 as a test set. A sliding window is used to acquire training and testing data. The window size is the sum of the historical and predicted time lengths, and the number of sliding steps is three and six for the training and testing phases, respectively. The World Meteorological Organization declares that the 6-h interval meets the global meteorological standards, which can ensure the uniformity and efficient processing of global data. The 6-hour interval can accurately reflect the weather changes and ensure the stability and efficiency of the prediction, making it the best choice for current weather forecasting. The sliding length of the training set is 3 to enrich and enhance the training set. We randomly select a part of the training set as the validation set, and the ratio of the training set to the validation set is 9:1. To account for the varying units in different data sources, which can negatively impact model training, we first normalize all source data via the data normalization method. The following equation illustrates our preprocessing approach:

$$\hat{y}=\frac{y-{y}_{mean}}{{y}_{std}}$$

(1)

where $\hat{y}$ and $y$ denote the preprocessed value and the original value of the variable, respectively, and ${y}_{mean}$, ${y}_{std}$ denote the mean and the standard deviation of the variable’s original value, respectively. Notably, because the elevation data of the ocean area represents the depth of the seabed, we use the zero-conversion method to address the elevation data of the ocean area to avoid the influence of this on capturing the role of land topography.

Preliminaries

We define the multivariate meteorological data fusion WSP problem as follows. Given that ${s}_{t}\in {R}^{C\times H\times W}$ represents the vector wind speed at time $t$, the $m$ wind speed prior to $t$ can be expressed as ${S}^{t-m,t}={\{{s}_{i}\}}_{t-m}^{t}\in {R}^{T\times C\times H\times W}$. $T$ denotes the time scale (here, $T=m$), $C$ represents the variable scale, $H$ represents the latitudinal height, and $W$ represents the longitudinal width. In this study, the vector wind speed is divided into u-wind and v-wind; hence, $C$ is two. In addition, we introduce geopotential, temperature, and elevation data as auxiliary variables, where $G{T}^{t-m,t}={\{g{t}_{i}\}}_{t-m}^{t}\in {R}^{T\times C\times H\times W}$ denotes temperature and geopotential data for the period $t-m$ to $t$ and where $E\in {R}^{H\times W}$ denotes elevation data. Suppose that we use wind speed, geopotential, temperature, and elevation data from $m$ historical times to predict the wind speed field at $n$ future points in time; this can be expressed as:

$${S}^{t+1,t+n}=\psi [{S}^{t-m,t};G{T}^{t-m,t};E]$$

(2)

where ${S}^{t+1,t+n}$ denotes the wind speed data from $t+1$ to $t+n$ and $\psi$ denotes the MFWPN. To realize the wind speed prediction for the next 24 h (n = 24), we set the time length of historical wind speed data to 24 h (m = 24). The past 24 h of data helps to identify trends and cyclical patterns in wind speed, such as diurnal variations and seasonal fluctuations, which may continue in the next 24 h. In addition, the short-term data simplify the complexity of the prediction model while better reflecting the sensitivity of short-term wind speed changes, making the prediction of future wind speeds more accurate. We referred to the relevant studies^15,33 and finally decided to use the historical 24-h wind speeds to forecast wind speeds in the next 24 h.

MFWPN

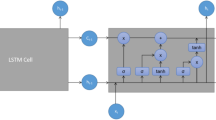
Figure 6 shows the overall network architecture of the MFWPN. In this work, multiple wind-related meteorological data are fused to perform more accurate vector wind speed estimation, as shown in Fig. 6. The input data include the vector wind speed ${F}_{Wind}\in {R}^{B\times T\times C\times H\times W}$, temperature and geopotential ${F}_{GT}\in {R}^{B\times T\times C\times H\times W}$, and geographic elevation ${F}_{E}\in {R}^{H\times W}$. Where B denotes batch size, C denotes the number of variables (${F}_{Wind}$ and ${F}_{GT}$ contain two variables, so C is 2), and H and W denote the number of grid points in the study area. Afterward, the input data are reshaped and fed into the encoder for spatial feature extraction of each meteorological dataset. Each encoder is packaged with a local convolutional and global attention encoder. The spatial features of elevation, geopotential, and temperature are then integrated via a multivariate spatial fusion module to correct the spatial features of the wind. Then, the time unit is used to capture the temporal evolution pattern, and the multivariate temporal fusion module is used to extract the precursor information of the wind evolution from the geopotential temperature evolution to correct the wind further. Finally, a decoder is used to decode the evolved wind spatial features to obtain the vector wind speed distribution at future moments.

Fig. 6: MFWPN network structure.

MFWPN consists of four parts: spatial encoder-decoder, time units, spatial fusion module, and temporal fusion module. The spatial encoder-decoder is used to extract and reconstruct the spatial features of the wind field. The time unit is used to realize the temporal evolution of the wind field. The spatial and temporal fusion modules are used to fuse the spatial and temporal effects of other meteorological factors on wind field evolution. The last module is a loss function designed according to the wind speed characteristics, which helps the network to complete the fitting more efficiently.

Local CNN unit

The evolution of the wind field is highly complex, containing local and global patterns. Global patterns reflect regularities and trends on a large scale, and local patterns reflect fluctuations on a smaller spatial scale. Convolutional neural networks have good feature extraction ability for local features. However, the local fluctuations of wind speed are more frequent, and traditional convolutional operations tend to lose some high-frequency components when extracting local information, which is not conducive to capturing the dynamics of the wind field and its evolution patterns. Therefore, we use an invertible neural network (INN)^63,64 to construct a local feature extractor for the wind field, whose network structure is shown in Fig. 6b. The INN allows interactive information transfer between input and output, can maintain feature integrity, and ensures that high-frequency information is adequately retained, especially subtle changes and local fluctuations in the wind field, such as sharp changes in wind speed, which are key features in the evolution of the wind field. Taking ${F}_{Wind}\in {R}^{B\times T\times C\times H\times W}$ as an example here, the transformation can be expressed as:

$${F}_{Wind}^{1},{F}_{Wind}^{2}=Split[{W}_{expand}(R({F}_{Wind}))]$$

(3)

$${F}_{Wind}^{3}={F}_{Wind}^{2}+[{W}_{inn}({F}_{Wind}^{1})]$$

(4)

$${F}_{Wind}^{4}={F}_{Wind}^{1}+[{W}_{inn}({F}_{Wind}^{3})]$$

(5)

$${F}_{Wind}^{L}={W}_{press}(Cat[{F}_{Wind}^{3};{F}_{Wind}^{4}])$$

(6)

where $R$ denotes the transformation of the scale from $B\times T\times C\times H\times W$ to $BT\times C\times H\times W$. ${W}_{expand}$ denotes the channel expansion convolution, which expands the original feature channel from $C$ to $C^{\prime}$. Referring to INN ^63,64, $C^{\prime}$ is set at 64. ${W}_{inn}$ denotes the inverse convolution intermediate convolution process, which contains a 3 × 3 convolution block, a 1 × 1 convolution block, and a 1 × 1 convolution. $Split$ denotes the segmentation computation, which splits the expanded feature into ${F}_{Wind}^{1},{F}_{Wind}^{2}\in {R}^{BT\times \frac{C^{\prime} }{2}\times H\times W}$. $Cat$ denotes feature splicing, and ${W}_{press}$ denotes channel compression convolution that compresses the variable channel back to $C$. Through feature splitting and merging, inverse convolution extracts features while preserving the original feature information as much as possible to avoid information loss. Finally, the localized features of the wind and auxiliary variables can be obtained as ${F}_{Wind}^{L}\in {R}^{BT\times C\times H\times W}$ and ${F}_{GT}^{L}\in {R}^{BT\times C\times H\times W}$.

Global SA unit

Wind fields are influenced by local climatic factors and regulated by large-scale meteorological systems. Changes in large-scale meteorological systems, such as the monsoon, determine the wind field’s overall movement pattern and long-term trend. Capturing the global pattern of the wind field and realizing the organic combination of local features and global patterns are especially important to reflect the spatial and temporal changes in wind speed accurately. Self-attention can directly model the long-range dependence between arbitrary positions in the input data and has significant advantages in extracting global patterns. Meanwhile, to balance the computational efficiency and performance of self-attention, we use the lite transformer block^63,65 as the basic unit of the global spatial unit, whose network structure is shown in Fig. 6b. Take the two-channel input ${F}_{Wind}\in {R}^{B\times T\times C\times H\times W}$ as an example, first reshape it to obtain ${\hat{F}}_{Wind}\in {R}^{BT\times C\times H\times W}$. Then, using 1 × 1 convolution and 3 × 3 depth-wise convolution to obtain $Q$, $K$, and $V$, which can be expressed as follows:

$$Q={W}_{1\times 1}^{Q}{W}_{3\times 3}^{Q}(LN({\hat{F}}_{Wind}))\in {R}^{BT\times C\times H\times W}$$

(7)

$$K={W}_{1\times 1}^{K}{W}_{3\times 3}^{K}(LN({\hat{F}}_{Wind}))\in {R}^{BT\times C\times H\times W}$$

(8)

$$V={W}_{1\times 1}^{V}{W}_{3\times 3}^{V}(LN({\hat{F}}_{Wind}))\in {R}^{BT\times C\times H\times W}$$

(9)

where ${W}_{1\times 1}$ and ${W}_{3\times 3}$ denote 1 × 1 convolution and 3 × 3 depth-wise convolution, respectively, and $LN$ denotes the normalization layer. Next, we dimensionally transform $Q$, $K$, and $V$ to obtain $Q^{\prime} \in {R}^{BT\times HW\times C}$, $K^{\prime} \in {R}^{BT\times C\times HW}$, and $V^{\prime} \in {R}^{BT\times HW\times C}$. The attention computation process can be summarized as follows:

$${A}_{weight}=V^{\prime} \cdot {{\mbox{Softmax}}}({{\mbox{K}}}^{\prime} \times {{\mbox{Q}}}^{\prime} /\alpha )\in {R}^{BT\times HW\times C}$$

(10)

$$\phi={W}_{1\times 1}^{A}(R({A}_{weight}))+{\hat{F}}_{Wind}$$

(11)

where ${A}_{weight}$ denotes the self-attention matrix, ${\mbox{Softmax}}$ denotes the SoftMax activation function, $R(.)$ reshape the ${A}_{weight}\in {R}^{BT\times HW\times C}$ to $BT\times C\times H\times W$, and $\phi$ denotes the self-attention output feature. Here, α is a learnable scaling parameter used to control the size of the dot product of $K$ and $Q$ before applying the SoftMax function. Afterward, feature transformation is performed via a regular feedforward network, which can be represented as follows:

$$\phi^{\prime}={\mbox{GELU}}({W}_{1\times 1}^{a}{W}_{3\times 3}^{a}(LN(\phi )))\odot {W}_{1\times 1}^{b}{W}_{3\times 3}^{b}(LN(\phi ))$$

(12)

$${F}_{Wind}^{G}={W}_{1\times 1}^{c}\,\phi^{\prime}+\phi$$

(13)

where $\odot$ denotes element multiplication, $LN$ denotes the normalization layer, GELU denotes the GELU activation function. The spatial feature output ${F}_{Wind}^{G}\in {R}^{BT\times C\times H\times W}$ of the self-attention branch is obtained after residual computation. Two learnable parameters are introduced to balance the global spatial features and local spatial features adaptively:

$${\chi }_{Wind}^{S}={\alpha }^{L}\cdot {F}_{Wind}^{L}+{\alpha }^{G}\cdot {F}_{Wind}^{G}$$

(14)

where ${\alpha }^{L}$ and ${\alpha }^{G}$ denote global and local weighting factors, respectively. The final outputs of the encoder are the vector wind speed spatial feature ${\chi }_{Wind}^{S}\in {R}^{BT\times C\times H\times W}$ and the geopotential temperature auxiliary feature ${\chi }_{GT}^{S}\in {R}^{BT\times C\times H\times W}$.

Multivariate spatial fusion module

The deterministic evolution law of wind speed refers to the fixed, periodic evolution law that can be modeled by relying on historical wind speed data and models. However, the wind speed system is a chaotic system, and the uncertainty evolution refers to the complexity and unpredictability of the wind speed system, which limits the accuracy of wind speed prediction by relying only on the historical wind speed. We would like to obtain some data from other sensors as a complementary fusion into the prediction model to further improve the wind speed prediction accuracy. According to the explanation in Data, geopotential and temperature are important meteorological factors affecting wind, and they work together to form the basis of wind speed variation through various mechanisms such as topography and turbulence. In a complex environment, the air temperature, geopotential, and elevation data contain some noise information on the wind, but more of the original force of the wind field evolution, so we correct the wind field characteristics based on the meteorological information extracted from them. When processing the time series, LSTM corrects the present data based on data from future time points, and its correction effect is generally verified and recognized. Inspired by the multigating mechanism of LSTM, we introduce this mechanism into the fusion module and let the meteorological information, such as geopotential, temperature, etc., correct the wind evolution characteristics through the cooperation of the forgetting gate and memory gate.

The Multivariate spatial fusion module is shown in Fig. 6c, which consists of spatial attention modules, a forgetting gate, a memory gate, and an elevation encoding block. After spatial coding, we obtain the spatial distribution characteristics of the geopotential, temperature, and vector wind speed as ${\chi }_{GT}^{S}$ and ${\chi }_{Wind}^{S}$. The SA block first filters the focused information of the geopotential and temperature to prevent noise interference. The focused wind spatial distribution is relayed to the network through sigmoid activation, which we call the forgetting gate $f$. Afterward, the supplementary features are obtained from the geopotential and temperature to obtain the spatial features of the wind through the memory gate $i$. The above process can be expressed as follows:

$$SA({\chi }_{GT}^{S})={W}_{7\times 7}(Cat[Avepooling({\chi }_{GT}^{S});Maxpooling({\chi }_{GT}^{S})])\in {R}^{BT\times 1\times H\times W}$$

(15)

$${f}_{GT}^{S}=\sigma [SA({\chi }_{GT}^{S})]\in {R}^{BT\times 1\times H\times W}$$

(16)

$${i}_{GT}^{S}=\sigma [SA({\chi }_{GT}^{S})]\times \,{{{\mathrm{Tanh}}}}({\chi }_{GT}^{S})\in {R}^{BT\times C\times H\times W}$$

(17)

where $SA$ denotes spatial attention computation, $Cat$ denotes feature splicing, $Avepooling$ and $Maxpooling$ denote average pooling and maximum pooling, $\sigma$ denotes the sigmoid activation function, and ${{\mathrm{Tanh}}}$ denotes the tanh activation function. To incorporate the controlling role of elevation data in the spatial characterization of winds, we coded the elevation data in the study area:

$$Ele=\sigma ({W}_{ele}(Stack({F}_{E})))\in {R}^{BT\times C\times H\times W}$$

(18)

where $Stack$ denotes the superposition of ${F}_{E}$ from $H\times W$ to $BT\times C\times H\times W$, ${W}_{ele}$ denotes the elevation data coding, and 1 × 1 convolution and 3 × 3 convolution blocks are used for adaptive coding. In summary, we obtain the wind spatial features corrected by the multivariate spatial fusion unit ${{\chi }^{\frown {}}}_{Wind}^{S}\in {R}^{BT\times C\times H\times W}$:

$${{\chi }^{\frown {}}}_{Wind}^{S}={\chi }_{Wind}^{S}\times {f}_{GT}^{S}+{i}_{GT}^{S}+{\chi }_{Wind}^{S}\times Ele$$

(19)

Time unit

Like spatial evolution, the wind field has short- and long-term dependence on the time scale. Taking 24-h wind speed forecast as an example, diurnal variations can be interpreted as long-time climatic phenomena, and localized air currents can be interpreted as short-time variations. The accurate prediction of future wind speed can be realized only by realizing the grasp of the short-time dependence and the long-time trend. If an iterative prediction method is used, the long-time prediction will result in the accumulation of errors, while the direct prediction will lead to the inefficiency of the model. Therefore, we propose a time cell that can realize multi-step direct prediction, through which we capture the short-time fluctuation and long-time trend of wind field evolution and directly evolve the historical 24-h wind speed characteristics into the future 24-h wind speed characteristics. As shown in Fig. 6d, to fully capture the spatiotemporal evolutionary patterns of the wind, we employ large kernel convolution and inter-frame dynamic attention to design the time unit. We use the affine large kernel dilated convolution method^58,59 to extract the intraframe spatiotemporal evolution patterns of wind and auxiliary meteorological elements. According to the principle of the convolutional sensory field, the sensory field obtained by combining a $(2d-1)\times (2d-1)$ deep convolution and a $K/d\times K/d$ dilation convolution is comparable to that of $K\times K$. Therefore, in the upper branch of the time unit, we use 3 × 3 depth-wise convolution, dilated convolution, and 1 × 1 convolution to obtain the receptive field of the large kernel convolution to extract the in-frame spatiotemporal evolution law of the wind. Taking ${{\chi }^{\frown {}}}_{Wind}^{S}$ as an example, it is first reshaped to obtain ${z}_{0}=R({{\chi }^{\frown {}}}_{Wind}^{S})\in {R}^{B\times TC\times H\times W}$. The affine large kernel convolution process can be expressed as follows:

$${z}_{l+1}^{1}={W}_{1\times 1}({W}_{Dw-d}({W}_{Dw}({z}_{l})))\in {R}^{B\times TC\times H\times W}$$

(20)

where ${W}_{1\times 1}$ denotes a 1 × 1 convolution, ${W}_{Dw-d}$ denotes a depth-wise dilated convolution, and ${W}_{Dw}$ denotes a depth-wise convolution. In the lower branch, adaptive channel attention is used to regulate the interframe relationship of the wind speed spatiotemporal sequence:

$${z}_{l+1}^{2}={g}_{\varphi }(GAP({z}_{l}))\in {R}^{B\times TC\times 1\times 1}$$

(21)

where ${g}_{\varphi }$ denotes a one-dimensional convolution with convolution kernel $\varphi$, and $GAP$ denotes global average pooling. According to ECANet⁶⁶, $\varphi={|({\log }_{2}(TC)+1)/2|}_{odd}$. Afterward, the two branches of information are fused to obtain a time cell spatiotemporal feature output ${z}_{l+1}\in {R}^{B\times TC\times H\times W}$.

$${z}_{l+1}={W}_{1\times 1}(\sigma ({z}_{l+1}^{1})\odot {z}_{l+1}^{2})+{z}_{l}$$

(22)

After the evolutionary process of multiple time units, the output of the final time unit module is ${\chi }_{Wind}^{T}\in {R}^{B\times TC\times H\times W}$ and ${\chi }_{GT}^{T}\in {R}^{B\times TC\times H\times W}$.

Multivariate temporal fusion module

Fig. 6e shows the multivariate temporal fusion module, which consists of channel attention blocks, forgetting gates, and memory gates. After passing through the time unit, we obtain the time series evolution characteristics of the geopotential, temperature, and vector wind speed, ${\chi }_{Wind}^{T}$ and ${\chi }_{GT}^{T}$, respectively. We use the forgetting gate and memory gate to correct the wind field features from the temporal dimension and explore the foreshadowing wind speed evolution pattern caused by the temporal variation in temperature and geopotential. Similar to the multivariate spatial fusion module, the LSTM-style temporal fusion process can be expressed as follows:

$$CA({\chi }_{GT}^{T})=Linear(Avepooling({\chi }_{GT}^{T}))\in {R}^{B\times TC\times 1\times 1}$$

(23)

$${f}_{GT}^{T}=\sigma [CA({\chi }_{GT}^{T})]\in {R}^{B\times TC\times 1\times 1}$$

(24)

$${i}_{GT}^{T}=\sigma [CA({\chi }_{GT}^{T})]\times \,{{{\mathrm{Tanh}}}}({\chi }_{GT}^{T})\in {R}^{B\times TC\times H\times W}$$

(25)

where $Linear$ denotes a fully connected layer, $CA$ denotes the channel attention, which captures the temporally important information about the bit geopotential and temperature. In summary, we can obtain the output of the multivariate temporal fusion module as follows:

$${{\chi }^{\frown {}}}_{Wind}^{T}={\chi }_{W}^{T}\times {f}_{GT}^{T}+{i}_{GT}^{T}$$

(26)

Decoder

The structure of the decoder is similar to that of the encoder. The difference is that the decoder performs only spatiotemporal decoding of the vector wind speed feature ${{\chi }^{\frown {}}}_{Wind}^{T}\in {R}^{B\times TC\times H\times W}$, which incorporates information from multiple sources. Afterward, a linear transformation is performed to obtain the final wind speed distribution feature ${F}_{out}\in {R}^{B\times T\times C\times H\times W}$.

Composite loss function

Wind is a meteorological factor that fluctuates dramatically. The fluctuating wind speed at a given moment in a single image reflects alternating high- and low-frequency information. These switches pose a challenge for the MSE loss function to capture such high- and low-frequency information. Moreover, owing to the variability of the wind direction itself, global MSE loss has difficulty capturing the wind direction in a targeted manner. To adapt to the variability of the wind and enable MFWPN to better fit the wind pattern, a composite loss function was designed with a global MSE loss, a structural similarity (SSIM) loss, and a wind direction loss, as shown in Fig. 6f. The global loss can be expressed as:

$${L}_{Glo}={\Vert \hat{y}-y\Vert }_{F}^{2}$$

(27)

where $y$ denotes the true wind speed and $\hat{y}$ denotes the predicted wind speed. In imaging, the SSIM is often used to evaluate the quality of image generation. Considering each frame of the wind speed as a picture, the SSIM can focus on the spatial interrelationships of the wind speed at each observation point, including texture and edge information. Therefore, we introduce SSIM metrics from the image domain into our WSP loss to assist the network in better fitting the spatial fluctuations in the wind speed. The SSIM loss can be expressed as follows:

$${L}_{SSIM}=1-SSIM[\hat{y},y]$$

(28)

where $SSIM(.)$ denotes the SSIM calculation. To perform accurate wind direction prediction, we additionally introduced wind direction loss. The wind direction at an observation point can be calculated from the u-wind and v-wind components of the wind speed. Assuming that the u-wind and v-wind at an observation point are ${u}_{g}$ and ${v}_{g}$, the wind direction at that point can be calculated as follows:

$$Ang=\arctan ({u}_{g},{v}_{g})$$

(29)

The true and predicted wind directions can be expressed as follows:

$${y}_{Ang}=\arctan ({u}_{y},{v}_{y})$$

(30)

$${\hat{y}}_{Ang}=\arctan ({u}_{\hat{y}},{v}_{\hat{y}})$$

(31)

The wind angle loss can be obtained as:

$${L}_{Ang}=\left\{\begin{array}{c}{\Vert |\,{\hat{y}}_{Ang}-{y}_{Ang}|\Vert }_{F}^{2},|{\hat{y}}_{Ang}-{y}_{Ang}|\le 180\\ {\Vert 360-|\,{\hat{y}}_{Ang}-{y}_{Ang}|\Vert }_{F}^{2},|{\hat{y}}_{Ang}-{y}_{Ang}| > 180\end{array}\right.$$

(32)

Finally, the composite loss can be obtained as follows:

$$L={L}_{Glo}+{L}_{SSIM}+{L}_{Ang}$$

(33)

Evaluation methods

We used latitude-weighted RMSE, MAE, and ACC^15,56 to evaluate the accuracy of vector wind speed prediction.

$${{{\rm{RMSE}}}}=\frac{1}{{N}_{predictions}}{\sum }_{i}^{{N}_{predictions}}\sqrt{\frac{1}{{N}_{lat}{N}_{lon}}{\sum }_{j}^{{N}_{lat}}{\sum }_{k}^{{N}_{lon}}L(j){\left({{Y}^{\frown {}}}_{i,j,k}-{Y}_{i,j,k}\right)}^{2}}$$

(34)

$$MAE=\frac{1}{{N}_{predictions}}{\sum }_{i}^{{N}_{predictions}}\frac{1}{{N}_{lat}{N}_{lon}}{\sum }_{j}^{{N}_{lat}}{\sum }_{k}^{{N}_{lon}}L(j)\left\Vert {{Y}^{\frown {}}}_{i,j,k}-{Y}_{i,j,k}\right\Vert$$

(35)

$${{{\rm{ACC}}}}=\frac{{\sum }_{i,j,k}^{N}L(j)({\mathop{Y}^{\frown {}}}_{i,j,k}-\xi )({Y}_{i,j,k}-\xi )}{\sqrt{{\sum }_{i,j,k}^{N}L(j){\left({\mathop{Y}^{\frown {}}}_{i,j,k}-\xi \right)}^{2}\sum L(j){\left({Y}_{i,j,k}-\xi \right)}^{2}}}$$

(36)

$$L(j)=\frac{\cos (lat(j))}{\frac{1}{{N}_{lat}}{\sum }_{j}^{{N}_{lat}}\cos (lat(j))}$$

(37)

where ${N}_{predictions}$ denotes the predicted time length, ${N}_{lat}$, ${N}_{lon}$ denotes the number of grid points in latitude and longitude direction, $i$, $j$, $k$ denotes the time, width, and height index, $Y$ denotes the true value, and $\mathop{Y}^{\frown}$ denotes the predicted value. $\xi$ denotes the climate factor, defined as ${\xi }_{h,w}=\frac{1}{{N}_{predictions}}\mathop{\sum }_{i}^{{N}_{predictions}}{Y}_{i}$.

In addition, we introduced a more targeted metric, $WDF{A}_{\alpha }$, to measure wind direction prediction. For the H × W grid points to be predicted, we measure wind direction prediction by calculating the number of grid points in which error is less than a set threshold. The angle thresholds $\alpha$ are generally set to 90, 45, and 22.5. $WDF{A}_{\alpha }$ can be expressed as follows:

$$WDF{A}_{\alpha }=\frac{Count(diff(pred,true) \, < \, \alpha )}{H\times W}\times 100 \%$$

(38)

$$diff(pred,true)=\left\{\begin{array}{c}|pred-true|,|pred-true|\le 180\\ 360-|pred-true|,|pred-true| > 180\end{array}\right.$$

(39)

where $Count(.)$ denotes counting the number of eligible observations. For example, for 64 × 80 grid points in Northeast China, if 4800 grid points have an angular difference of less than 22.5 degrees, then $WDF{A}_{\alpha=22.5}=\frac{4800}{64\times 80} \times 100\%=93.75$.