Introduction

Colloidal III-V quantum dots (QDs) have shown great potential in recent years as a light-emitting source for both optoelectronic applications and quantum optics1,2,3,4. High-quality ternary In1-xGaxP QDs, a model alloy system, in which the In-to-Ga ratio can be used to tune absorption and emission, have been synthesized via a diffusion-limited Ga-incorporation process in molten-salt solvents5,6,7. The static electronic structure of these alloyed QDs, like all QDs8, is determined by both quantum confinement and the electronic structure of the underlying bulk material5. As shown in previous work5, the In1-xGaxP QD system demonstrates a continuous composition-driven direct-to-indirect bandgap transition similar to its bulk alloy counterpart, which changes the QD exciton level structure and the oscillator strengths of each excitonic transition. Much effort has been devoted to engineering the composition of ternary In1-xGaxP QDs to tune optical properties, such as transition energies, photoluminescence (PL) quantum yield, and radiative lifetimes5. The effect of QD size on exciton–phonon coupling (EXPC) and exciton relaxation dynamics has also been extensively studied, particularly in model QD systems like CdSe9,10,11,12. The effect of alloying on dynamics, however, cannot be sufficiently described by the conventional model for light–matter interactions in binary III-V or II-VI QDs, where excitons are formed upon excitation to a ‘bright’ spin-allowed state and relax down to a ‘dim’ spin-forbidden state that contributes to a red-shifted emission to the ground state13,14,15. This three-level model captures the temperature-dependence of PL lifetime in InP and CdSe QDs, but its treatment of the bright state as a single state is an oversimplification. The exciton fine structure and the high density of ‘dim’ states19 is more prominent in In1-xGaxP systems because alloying lifts the degeneracy of crystal symmetry5,16. Consequently, the exciton level structure and relaxation channels within the manifold of bright excitons of alloyed III-V QDs require further investigation.

The change of exciton level structure distinguishes EXPC in ternary QDs from that in binary QDs. In semiconductors, the cooling of high-energy (‘‘hot’’) excitons via phonon interactions serves as an important non-radiative relaxation channel. Quantum confinement by finite size in QDs leads to energy discretization and blurs the definition of momentum. The resulting EXPC creates a phonon bottleneck in the relaxation dynamics and gives rise to a wide range of coherent phenomena in QDs17,18,19,20. This effect is absent in bulk semiconductors, where energy and quasi-momentum are transferred between charge carriers and phonons through Fröhlich-type and deformation-potential-type interactions21,22,23. Extensive research has focused on quantifying EXPC and understanding how this coupling influences the hot exciton cooling process and other relaxation channels, particularly in model QDs, such as CdSe10,11,12,24,25,26,27,28,29,30,31,32,33,34,35. The atomistic pseudopotential theory has been used to generate detailed insights into the electronic structure and dynamical processes of a wide range of nano-heterostructures and alloys, owing to its atomistic nature and transferability across materials. Combined with methods for simulating dynamics in open quantum systems, this theoretical approach has advanced our understanding of energy transfer processes and underlying mechanisms in nano-materials past continuum effective mass theory, as it calculates excitonic state-specific EXPC with access to deep-band excitonic states24,25,36,37,38. Experimentally, EXPC can be resolved through quantum coherence in time-resolved spectroscopy methods, such as transient absorption (TA) spectroscopy and two-dimensional electronic spectroscopy (2DES), where oscillatory decays at frequencies matching phonon modes appear on femtosecond to picosecond timescales following photoexcitation39,40,41,42,43,44. This time-domain method directly probes intrinsic EXPC events prior to carrier trapping9,45,46. The role of quantum coherence in the photophysical properties of QDs remain an active area of research40,41,42,47. As absorptive techniques can access excited states of higher energy, coherence analysis is complementary to steady-state single-particle PL spectroscopy, which only shows the coupling strength of emissive states to different phonon modes13,48.

In this work, we investigate the influence of alloy composition on exciton level structures, EXPC and femtosecond exciton relaxation dynamics in In0.62Ga0.38P/ZnS (38% Ga) and In0.35Ga0.65P/ZnS (65% Ga) QDs using coherent 2DES measurements and atomistic theoretical calculations. We describe the exciton level structure by integrating an atomistic semi-empirical pseudopotential model with the Bethe–Salpeter equation (BSE). Inspired by the unusual direct-vs-indirect gap transition across the two compositions of In1-xGaxP QDs, we map QD exciton densities onto the bulk Bloch wavefunctions and quantify the ‘quasi-momentum’ of high-energy QD excitons. We calculate excitonic state-specific EXPC, decouple contributions from optical and acoustic phonon modes, and find that direct-gap QD excitons couple more strongly to optical phonons than indirect-gap excitons. Optical phonons and their EXPC are also measured using Raman spectroscopy with resonant excitations49,50. Raman analysis and pseudopotential calculations show excellent agreement on longitudinal optical (LO) phonon Huang-Rhys factors, with similar values for 38% and 65% Ga QDs. Hot exciton relaxation dynamics, extracted from 2DES data and polaron-transformed Redfield calculations, show faster relaxation time in 65% Ga QDs compared to 38% Ga QDs, with qualitative agreement between theoretical modeling and 2DE measurements. We pinpoint the interplay between exciton level structure and EXPC as the key factor influencing both the timescale of this process and the energy-retaining states that slow down charge carrier relaxation in 38% Ga QDs. Using beating map analysis, we correlate vibronic coherences at the LO phonon frequency with the emissive states in both samples and find that LO phonons in 65% Ga QDs interact with a narrower energy range of excitons than those in 38% Ga QDs. We attribute this observation to closer exciton energy levels with reduced spacings in 65% Ga QDs, which likely facilitate exciton relaxation and decoherence events, especially when the energy spacing is less than one phonon quanta. These findings show that, apart from bandgap engineering, alloying intricately tunes non-radiative exciton dynamics and EXPC in III–V QD systems via energy levels, which can be precisely predicted by electronic structure calculations and dynamics simulations. These metrics, namely hot exciton cooling dynamics and EXPC, should be taken into consideration in the design of novel alloyed QD systems.

Results and discussion

Steady-state characterization and modeling

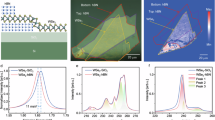
Synthesis and characterization of In0.62Ga0.38P/ZnS and In0.35Ga0.65P/ZnS QDs are reported elsewhere and the samples studied here are identical to those reported5. Samples with the same core size (4.92 nm) were chosen to avoid size-dependent excited state dynamics and EXPC9. In and Ga cations were alloyed uniformly, as validated by solid-state nuclear magnetic resonance and computational modeling5. As shown in Fig. 1, both samples feature a broad excitonic transition in the ensemble steady-state absorption spectra. Emission peaks are at 1.88 and 1.96 eV for 38% Ga and 65% Ga QDs, respectively, where the blue shift is a result of bandgap widening with increasing Ga concentration. The broad exciton features observed in the experimental spectra were attributed to the size, shape and symmetry inhomogeneity of the QD ensemble5.

Fig. 1: Optical spectra and phonon reorganization energies for In1-xGaxP QDs.
figure 1

Absorption and emission spectra of a 38% Ga and b 65% Ga quantum dots (QDs) from experiments (solid lines) and theory (dashed lines) are shown. In the top panels, the exciton states are represented as bars with height corresponding to oscillator strength (OS). Exciton states labeled in green are assigned as ‘direct-like,’ while states labeled in purple are assigned as ‘indirect-like.’ Shaded gray region is the white light spectra used in the two-dimensional electronic spectroscopy (2DES) measurements. Shaded blue box in (a) highlights the ‘energy-retaining’ states in 38% Ga with high phonon reorganization energy. Bottom panel shows the phonon reorganization energy of exciton states in bar representation. Atom colors: blue—In, orange—Ga, olive green—P.

Full size image

Theoretical calculations reveal the detailed exciton level structures in the alloyed QDs. Exciton states were calculated using the atomistic semi-empirical pseudopotential method combined with the BSE to account for electron–hole correlation5,51,52,53,54. We use the same pseudopotentials of In, Ga and P as reported in ref. 5. These atomistic pseudopotentials were fitted to accurately reproduce ab initio bulk band structures and deformation potentials (Fig. S1)5. We omitted modeling of the wide bandgap ZnS shell to reduce computational cost. The stochastic filter diagonalization method was used to selectively obtain the electron and hole states near the band edge with high accuracy and at reduced computational cost55. Oscillator strengths were calculated from the transition dipole moment between the ground and exciton wavefunctions, and are shown as the height of the colored bars above the energy axis in Fig. 1. More details on the semi-empirical pseudopotential method, the equilibrium QD configurations, and BSE and oscillator strength calculations can be found in the SI. Motivated by the composition-driven direct-to-indirect gap transition in alloyed In1-xGaxP QDs, we evaluated the ‘majority representation’ coefficients of exciton states by projecting the QD wavefunction onto the Bloch wavefunctions of bulk GaP at the direct (Γ) and indirect (X, L) valleys (Fig. S3)56,57. We classify each exciton transition as either ‘direct-like’ or ‘indirect-like’ (green and purple in Fig. 1), disentangling their different contributions to exciton structure and EXPC. More details regarding calculations of the majority representation coefficients are discussed in the SI.

Absorption and emission spectra were calculated from exciton energies, OS, and phonon reorganization energy (discussed below), and agreed well with the absorption onset energies and emission peak energies of the measured spectra. The broad exciton features observed experimentally are attributed to the presence of multiple bright states near the band edge, with more energetically dispersed bright states in 65% Ga QDs compared to 38% Ga QDs. Inhomogeneity of QD ensembles in terms of size, shape, and crystal symmetry could also contribute to this broad exciton feature5,40. Both QDs exhibit bright direct-like excitons at the band edge, while 38% Ga QDs have larger overall OS, in agreement with previous work on composition-driven transitions in In1-xGaxP alloyed QDs5. In addition, both compositions have clustered indirect gap-like exciton peaks at higher energies with smaller OS. The energy separation between direct gap-like and indirect gap-like excitons is smaller for 65% Ga QDs due to their density of exciton states. This result is consistent with Vegard’s law on the interpolation of conduction band minimum energy according to Ga content.

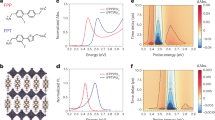
Phonons and their coupling to electronic states were characterized by Raman spectroscopy with resonant excitations, where the optical phonons were resolved (Fig. S4). For 38% Ga QDs, the peak of highest intensity at 347 cm−1 is assigned as the LO phonon mode, with the second overtone peak experimentally resolved. We extracted the peak area by fitting each with a sum of Gaussian functions and calculated an experimental Huang–Rhys factor of 0.30 using the peak area ratio. This factor is a measurement of EXPC assuming a displaced harmonic oscillator model, which provides a numerical strength of overall electronic transition coupling to the LO phonons, complementary to theoretical spectral density analysis58,59. The LO phonon for 65% Ga QDs is at 350 cm−1 and, due to higher Ga concentration, vibrates at a higher frequency than that for 38% Ga QDs. The experimental Huang–Rhys factor is calculated as 0.29, similar to that of 38% Ga QDs. The Huang–Rhys factors for LO phonons were also calculated from the atomistic theoretical modeling (0.25 for 38% Ga, 0.34 for 65% Ga), and agree well with experiments. The similar EXPC strength obtained from both modeling and Raman spectroscopy suggests that EXPC is not the main factor contributing to the decrease of quantum yield with increasing Ga content (reported in the previous study)5. Rather, the inevitable introduction of indirect gap-like transitions due to Ga incorporation is more detrimental to the quantum yield.

Theoretically calculated phonon mode frequencies and EXPC were in excellent agreement with the Raman results. We used a previously parametrized Tersoff-type force field to relax the QD geometries and obtain normal modes from the mass-weighted Hessian matrix5,60. EXPC were calculated directly from the semi-empirical pseudopotential model with phonon modes obtained from the classical force field5,59. Our model was parametrized based on the bulk deformation potentials and does not explicitly account for Fröhlich and piezoelectric coupling mechanisms. We are working on including long-range Coulomb components in our pseudopotential model to more accurately capture the Fröhlich-type interactions in III–V semiconductors38. The vibrational density of states for both 38% and 65% Ga QDs shows a clear ‘phonon gap’ at around 250–350 cm−1, separating the acoustic and optical phonon branches, as expected from the phonon dispersion relations of bulk InP and GaP61. The calculated LO phonon frequencies of 65% Ga QDs are slightly higher than the 38% Ga LO phonon frequency, which is consistent with the assignment of the experimental Raman peaks. The calculated EXPC elements agree qualitatively with the experimentally extracted Huang–Rhys factors for the LO phonons and provide more elaborate details on the diagonal and off-diagonal (inter-exciton) couplings (Fig. 1 and SI)59. The reorganization energies, which quantify the energy associated with lattice rearrangement upon vertical excitation from the ground state to a specific exciton state, are calculated for both QDs and plotted on the bottom panels of Fig. 15. Overall, 38% and 65% Ga QDs have similar reorganization energies (see Figs. S5, 6). Acoustic phonon contributions to the reorganization energy outweigh optical mode contributions due to their low frequency. Electron channel coupling is larger for indirect gap-like states; however, as hole channel coupling dominates the total EXPC, there is no significant difference in reorganization energies between direct-like and indirect-like exciton states (see Figs. S7–9)37,59,62. Optical phonon couplings are noticeably smaller for indirect gap-like excitons, while the acoustic phonon couplings are similar for indirect-like and direct-like excitons, which is consistent with the k-dependence of EXPC in bulk polar semiconductors. In 38% Ga QDs, the excitonic states between 1Sh–1Se (around 1.8–1.95 eV) and 1Ph-1Pe (around 2.05–2.3 eV) states, where the notation is modified based on the notation used in the effective mass model for spherical InP QDs63,64,65, exhibit larger reorganization energy, while similar states with large EXPC are absent in 65% Ga QDs (Fig. 1). The calculated EXPC for each exciton–phonon pair, along with the exciton level structure and reciprocal space decomposition, provides a clear picture of how electron–phonon coupling in bulk materials translates to confined alloyed nano-systems.

2DE spectra

The femtosecond excited state dynamics of 38% and 65% Ga QDs were measured using 2DES at room temperature under the single-photon excitation regime. Details of the home-built 2DES apparatus can be found in the Methods section and also elsewhere66. The broadband excitation is compressed to provide a near transform-limited pulse duration of 7.3 fs, which enables detection of ultrafast exciton relaxation in QDs (Fig. S10). The time separation between two excitation pulses gives rise to an additional excitation energy axis, which yields a frequency–frequency correlation map at each waiting time67,68,69. The simultaneous excitation of all exciton states within the excitation range also leads to various coherent phenomena within the excited states17,47. The time evolution of 2DE spectra for 38% and 65% Ga QDs within the first 1 ps upon photoexcitation is shown in Fig. 2. After the initial transient grating response, signals for both 38% and 65% Ga QDs form within the first 100 fs, with minimal spectral shift observed after signal formation is complete. The 2DE line shape of an elongated oval along the diagonal is a result of multiple excitonic levels with close energy spacing, and the presence of electronic inhomogeneity, giving rise to an energetically broad ground state bleaching (GSB) signal along the diagonal of 2DE spectra36,40,70,71,72,73. The off-diagonal width is influenced by the homogeneous linewidth of excitonic states and their couplings74. At 48 fs, multiple peaks are observed for both samples along the diagonal with off-diagonal peaks indicating the couplings. These peaks may correspond to the increased number of bright states related to the exciton fine structure, which has also been observed in InP/ZnS2 and CdSe QDs3, although scatter in the coherence time domain complicates the assignment. These peaks later broaden and evolve into a single broad peak on the 2DE spectra. This spectral lineshape, which is different from that of CdSe QDs36,44,71,72,73, is due to the overlap of off-diagonal peaks, indicating exciton state–state coupling, among closely spaced exciton levels40.

Fig. 2: 2DE spectra and diagonal time traces of 38% and 65% Ga QDs.
figure 2

Absorptive 2DE spectra (normalized with respect to each data cube) at waiting times 48, 100, 500, and 1000 fs for a 38% Ga QDs and b 65% Ga QDs. c Diagonal decay of the absorptive signal at [2.03 2.03] eV for (top) 38% Ga and (bottom) 65% Ga QDs. Both decays are fit with single exponential function to extract the time constant for hot exciton cooling process.

Full size image

A significant difference in the early-time 2DE spectra of 38% and 65% Ga QDs is observed at 500 fs, where the upper part of the 65% Ga QD signal (excitation and detection energies are above 2.08 eV) has a smaller signal amplitude than the lower region of the signal. We exclude the possibility of fast population dynamics by comparing the time evolution of the signal at two excitation energies, which shows a marginally faster decay component at early timepoints (Fig. S11). This fast decay is later assigned as non-radiative exciton cooling (elaborated upon in the next section), and its overall timescale is extracted through singular value decomposition (SVD) analysis (Figs. S12–S15). Therefore, the lower signal amplitude is due to the lower oscillator strength of exciton states at this energy range, as also shown in the computed exciton level structures. Previous picosecond TA measurements of this composition5 reported a transition from GSB to excited state absorption at around 30 ps at the same spectral location as this low oscillator strength region, a transition which we also observe in the 2DES and TA picosecond dynamics of the current work (Figs. S12 to S15). In 38% Ga QDs, the oscillator strength of indirect-like and direct-like exciton states are more comparable, which leads to relatively homogenous features in their 2DE spectra.

Exciton cooling dynamics

The fast exciton dephasing and non-radiative relaxation channels require further mechanistic investigation. Therefore, we calculated the phonon-mediated hot exciton cooling dynamics at the same energy range as the 2DE signals shown in Fig. 2. We obtained the EXPC matrix elements from the theoretical model and simulated the multi-phonon mediated hot carrier cooling dynamics using the polaron-transformed Redfield equation25. Our model focuses on the population dynamics (diagonal elements of the density matrix) and does not include coherent dynamics (off-diagonal elements). The excitation energies (initial states) were chosen as 0.25–0.3 eV above the band edge exciton to match the energy range of 2DE signals. Time traces of the total energy loss to phonons for 38% and 65% Ga QDs are plotted in Fig. 3a, b. The 38% Ga QDs show slower exciton cooling (245 fs) than 65% Ga QDs (91 fs), which is consistent with SVD analysis of 2DE dynamics. In the SVD analysis, the secondary principal component corresponds to dephasing and exciton cooling processes (SI SVD analysis), and the associated time constants are 421 and 189 fs for 38% and 65% Ga QDs, respectively. The population dynamics and lifetimes of each energy window of excitons (Fig. 3e, f) match well with the lifetimes extracted from the diagonal time trace of the 2DE spectra (Fig. S18).

Fig. 3: Simulated exciton cooling dynamics of 38% Ga and 65% Ga QDs.
figure 3

a, b Overall energy loss upon initial excitation with all phonons considered as compared to acoustic modes only. 38% Ga QDs show an overall energy loss time of 245 fs with all phonons considered in the calculation, and this time constant increases to 1936 fs when only acoustic phonon modes are considered. 65% Ga QDs show a faster energy loss time of 91 fs with all phonon modes considered, and this time constant decreases to 580 fs when only acoustic phonon modes are considered. c and d The calculated excitonic density of states over 1000 fs show population dynamics of (c) 38% Ga QDs excited at 2.12 eV and (d) 65% Ga QDs excited at 2.20 eV. e and f Comparison of simulated and experimental lifetimes for hot exciton cooling dynamics with varying excitation energy for e 38% Ga and f 65% Ga QDs.

Full size image

The distinct exciton cooling lifetimes of the two compositions are explained by the intricate interplay between exciton level structure and EXPC strength. In 38% Ga QDs, the presence of a larger energy gap between the 1Sh–1Se and 1Ph–1Pe states slows relaxation into the band edge (1.85 eV). Meanwhile, strong diagonal EXPC of states within this gap at ~2.02 eV (0.17 eV above the band edge) leads to large reorganization energies, which further stabilizes and retains energy in these states, as shown in Fig. 3c, d. In addition, due to the strong off-diagonal EXPC in 38% Ga QDs, energy is initially (before 50 fs) transferred to excitons with higher energy, leading to an initial increase in total energy followed by energy loss. Further, if optical phonons are removed from the calculations, the exciton cooling becomes significantly slower (6–10-fold) for both 38% and 65% Ga QDs (Fig. 3a, b), indicating the importance of the optical phonons in the cooling process.

Simulated exciton lifetimes for the diagonal signals of the 2D spectra (Fig. 3e, f) were determined by preparing the initial excited state at each excitation energy window and monitoring the population decay. The exciton lifetime of all energy windows for 38% Ga QDs is longer than that for 65% Ga QDs, supporting our finding that the phonon-assisted exciton cooling rate is faster for 65% Ga QDs. Our simulations for 65% Ga QDs indicate that excitons with higher energies have shorter lifetimes, which can be attributed to the higher density of excitons and the larger number of relaxation pathways (especially those mediated by optical phonons) for high-energy excitons. The experimental exciton lifetimes for 65% Ga QDs show overall excellent agreement with theory, with a less pronounced decreasing trend. This agreement is attributed to the truncation of upper boundary excitonic states in our simulations, which limits the up-conversion pathway for the 65% Ga system. For 38% Ga QDs, both the experimental and calculated lifetimes follow a nonmonotonic trend with a maximum observed at ~2.0 eV. This nonmonotonicity in the 38% Ga system is attributed to ‘population retaining’ excitons between 1Sh–1Se and 1Ph–1Pe states (at ~2.02 eV) that slow down exciton cooling. The agreement between simulations of pristine alloyed QDs and experiments on femtosecond-timescale exciton dynamics and steady-state characterization (optical and Raman spectra) also demonstrates that our synthesis methods yield high quality samples with minimal defects. The presence of multiple defects would otherwise alter the exciton cooling dynamics and affect the optical and Raman spectra results.

Optical phonon coherence analysis

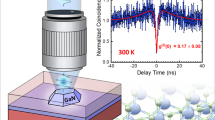
Under coherent excitation conditions, excitons interact with optical phonons leading to oscillatory decay traces in both samples (Figs. S19 and S20). In both diagonal and off-diagonal regions of 2DE spectra for 38% Ga QDs (Fig. S19), oscillatory signals with exponential decay dynamics are identified within the first 500 fs. This oscillation frequency can be obtained by subtracting the population dynamics and then Fourier transforming to the frequency domain. As shown in Fig. S19b, the unphased absolute-valued decay at excitation energy 2.09 eV and detection energy 2.03 eV ([2.09 2.03] eV) shows oscillation with exciton relaxation. By Fourier transforming the oscillation residual to the frequency domain, a beating spectrum at [2.09 2.03] eV is obtained, clearly showing that oscillations peak at ~358 cm−1. This oscillation residual can also be fitted with a damped oscillation function (Table S3), yielding a frequency of 361 ± 5 cm−1 and decoherence time of 221 ± 60 fs. This result shows that the observed oscillation is at the LO phonon frequency of 38% Ga QDs due to exciton-LO phonon interactions. Beating analysis at two other spectral locations (Fig. S19a, c) both pinpoint the oscillation at the LO phonon frequency (Table S3). Coherences are not observed in the simulated dynamics because our model treats phonon modes as the pure bath degree of freedom and assumes a thermal distribution of the initial phonon population.

We therefore extract the oscillation intensity at the LO phonon frequency across the entire excitation and detection energy range, which yields a beating map for 38% Ga QDs at LO phonon frequency (Fig. 4a). This beating map correlates the beating intensity (colored area) with the spectral information (contour lines) in 2DE spectra. As shown in Fig. 4a, quantum beats are present across the entire spectral range of the signal for 38% Ga. In particular, vibronic coherences are more pronounced at lower excitation energy, where the exciton states are closer to the band edge and emission states. This observation suggests that the exciton states near the band edge interact more strongly with the LO phonons, which also agrees with the calculated spectral density analysis discussed earlier. The excitation energy-dependent oscillation amplitudes reflect the strengths of vibronic coherences and corresponding exciton–phonon interactions. The beating intensity map overlaps with both diagonal and off-diagonal spectral regions, where the excitation and detection energies are separated by zero (diagonal), one (below-diagonal), or two (above-diagonal) LO phonon quanta, resembling vibronic energy levels. In particular, the excitation energy of the above-diagonal spectral region matches well with the emission maximum at room temperature. This pattern, with extracted decoherence time of ~200 fs, corresponds to the coherence between the zeroth and first, as well as first and second vibronic states and suggests the observed coherence is likely of vibronic origin. However, thermal effects complicate the assignment as excited vibrational energy levels for LO phonons are thermally populated at room temperature (Fig. S21). It is likely that both vibronic and vibrational coherences contribute to the observed oscillations, where the fine line relates to the extent of state mixing and origin of the ground or excited potential energy surface. While measurements at low temperature are required to separate the contributions from specific pathways following Feymann diagrams in Liouville space, this beating map reveals that LO phonons in 38% Ga QDs intrinsically interact with a wide energy range of exciton levels, further supporting an important role for optical phonons in femtosecond-exciton cooling processes.

Fig. 4: Beating map analysis of 38% Ga and 65% Ga QDs generated from absolute-valued 2DES data.
figure 4

a Beating maps of 38% Ga QDs at (top) LO phonon frequency (356 cm−1) and (bottom) 490 cm−1. The summed beating intensity at 356 cm−1 is 4787. b Beating maps of 65% Ga QDs at (top) LO phonon frequency (356 cm−1) and (bottom) 490 cm−1. Under the same normalization scheme, the summed beating intensity decreases to 933.

Full size image

For 65% Ga QDs, the beating signals are more localized at a particular above-diagonal region of the 2DE spectra, where the excitation energy is lower than the detection energy by one LO phonon quanta (Fig. 4b). The dominant beating frequency matches with the LO phonon, but the average decoherence time is faster, which is commensurate with the faster exciton cooling lifetime of 65% Ga QDs (Table S4; Fig. S20). This comparable duration suggests that the two processes might be correlated. The LO phonon energy difference (3 cm−1) between 38% and 65% Ga QDs is beyond the frequency resolution of beat spectra due to the chosen time sampling in waiting time. By generating the beating map of 65% Ga QDs at the LO frequency, we found that the excitation energy of the spectral region with the highest beating intensity matches well with the energy of emission maxima at room temperature, which is consistent with the observations in 38% Ga QDs. Although 65% Ga QDs show high beating intensity near [1.95 2.02] eV, the summed beating intensity in their beating spectrum is lower than that for 38% Ga QDs. We attribute the reduced excitation energy range for LO phonon coherence to the reduced exciton energy spacings in 65% Ga QDs, where densely packed energy levels create a natural scaffold for exciton relaxation and decoherence events. We also identify a beating signal at 490 cm−1 that is only present in 65% Ga QDs, which will be discussed in detail in a separate publication. Overall, the different beating intensity distributions and decoherence times between the two In-to-Ga compositions are consequences of the different exciton level structures and exciton-LO phonon interactions due to alloying.

In conclusion, we have demonstrated the effect of alloying on excited state dynamics and EXPC in emissive In1-xGaxP QDs with two alloying compositions (38% and 65% Ga) using 2DES and theoretical computations. Incorporation of Ga not only decreases the oscillator strengths of the emissive states, but also introduces complex exciton level structures and dynamics beyond the simple effective mass model. The distribution of direct gap-like and indirect gap-like exciton states follows the same trend as bulk In1-xGaxP semiconductors, where 65% Ga QDs show more indirect-like excitons near the band edge with low oscillator strength as compared to 38% Ga QDs. Higher Ga content also results in lower oscillator strengths of exciton states at higher energy, which leads to unique 2DE spectral lineshapes for 65% Ga QDs. Due to the high density of states and close energy spacings of excitons, optical phonons play a significant role in the femtosecond non-radiative exciton cooling process. In particular, 38% Ga QDs show slower hot exciton cooling due to the presence of ‘energy-retaining’ excitons between the 1Sh–1Se and 1Ph–1Pe states, as shown in both experiment and theoretical calculations. We report qualitative exciton level-dependent intrinsic exciton-LO phonon coupling strength using beating maps from 2DES measurements, where differences between two In-to-Ga ratios are observed despite their similar Huang–Rhys factors. Coherences at the LO phonon frequency are present in a wide range of exciton energy levels in 38% Ga QDs, whereas the coherences are mostly localized near the lowest two exciton states in 65% Ga QDs. We attribute this difference to the fact that the more closely spaced exciton energy levels in 65% Ga QDs facilitate the hot exciton cooling and decoherence processes. Overall, the composition of alloyed In1-xGaxP QDs tunes exciton energy spacings and available phonon energies. The interplay between these factors determines EXPC and phonon-assisted relaxation dynamics in this model alloyed QD, suggesting that alloying is an important tool for engineering excited state dynamics and electronic coherences in addition to excited state energies in semiconducting QD systems.

Methods

Theoretical calculation of In1-xGaxP QD excitonic structure and dynamics

The configurations of the In1-xGaxP alloyed QDs in the theoretical calculations were constructed following the same process as in previous work5. Random In-to-Ga replacements were performed on tetrahedral-shaped zinc-blende InP nanoclusters up to the desired alloy composition. The configurations were then minimized using a Tersoff-type classical force field60 and passivated with pseudo-ligand potentials on the surface. Configurations of In597Ga368P816 (38% Ga) and In339Ga626P816 (65% Ga) with random cation distribution were used in all computations of this work. For describing the excitonic states and energies, we integrated a semi-empirical pseudopotential model with the BSE. The pseudopotential function form and parameters for In, Ga, and P are described in the Supplementary Information5, where they were fitted to the ab initio bulk band structures and deformation potentials of relevant binary semiconductors (i.e., InP and GaP). The stochastic filter diagonalization technique was then used to obtain the electron and hole states near the band edge of each QD, with high accuracy and reduced computational cost55. We also categorized the exciton states according to their electronic structure decomposition in the reciprocal space by expanding the QD wavefunctions in the basis of Bloch wavefunctions of bulk GaP (or InP) at the Γ, X, and L valleys of the conduction band56,57. The full details of the calculation procedure and the extraction of OS, Raman spectra, the reciprocal-space representation, exciton phonon coupling and Huan–Rhys factors are detailed in the SI. For the population dynamics, a unitary polaron transformation is employed on the QD Hamiltonian, which helps to rescale the coupling between phonon modes and excitonic state and allows the description of multi-phonon relaxation in the lowest-order perturbation theory. After polaron transformation, the equation of motion for the reduced density matrix representing the Hilbert space of the excitonic states is given by the non–Markovian time–local secular Redfield equations.

Raman spectra

Raman spectra of 38% and 65% Ga QDs were collected with a confocal Raman microsystem in backscattering geometry at GSECARS, Advanced Photon Source, Argonne National Laboratory with a 532 nm (Laser quantum) excitation source with 63 mW power, in conjunction with a spectrometer (Acton SpectraPro, SP-2500, 1200 grooves/mm grating) and PIXIS100 back-illuminated deep depletion CCD camera at room temperature (300 K). The spectral data was obtained using a 5 × and 20 × objective (Mitutoyo) under parallel configuration to maintain polarization of the excitation laser and Raman scattering light. Detailed information regarding this acquisition apparatus has been reported previously75. Average exposure time was 300 s. The samples were drop casted on quartz substrates and remained stable throughout the spectral acquisition process.

Description of 2DES measurements and data processing

2DES was performed using a home-built apparatus reported previously66. A Ti:sapphire regenerative amplifier (Coherent, Inc.) seeded with a Ti:sapphire mode-locked oscillator (Coherent, Inc.) at 80 MHz repetition rate generates the fundamental lasing beam at 5 kHz repetition rate with pulse width of ~38 fs and center wavelength of ~800 nm. This pulse is subsequently sent to a 2 m tube of Ar gas at ~20 psi to generate the broadband excitation source from 450 to 900 nm, which is further cut down to 450 to 720 nm by an angle-tunable dichroic filter and compressed to ~7.3 fs full width at half maximum. The 2DE spectra at a given waiting time T in this study were acquired by collecting varying the first time delay from -90 to 90 fs with 1.5 fs time step, with an average pulse energy of ~32 nJ/pulse and spot size of 300 μm in diameter (~45 μJ/cm2). The colloidal QDs in methylcyclohexane were held in a quartz sample cell (Starna Cells) with 200 μm path length in an optical cryostat (Oxford Instruments) filled with N2 to minimize surface oxidation. Full details of the acquisition protocol and data reduction are found in the SI.