Introduction

The AI revolution has highlighted the shortcomings of today’s computing hardware. AI leaders have argued1,2 that machine learning is currently stuck in a local optimum, and if the field could move away from current digital hardware, then a global optimum could be reached. Analog computing offers an appealing alternative to today’s digital computers, both in terms of energy efficiency, and also potentially in terms of processing speed, if one can match the physics of the analog hardware to the mathematics of the AI algorithms. Several analog, physics-based computing demonstrations have focused on optimization3,4,5,6,7,8,9,10,11.

Probabilistic AI is an especially compelling use case for analog hardware. This branch of AI deals with Bayesian inference, uncertainty quantification, and sampling tasks and has led to recent breakthroughs in generative AI like diffusion models. However, it has been noted to struggle with computational difficulty on current digital hardware12,13. Interestingly, the mathematics of probabilistic AI happens to match that of thermodynamics14, which is the branch of classical physics that involves stochastic dynamics.

The relevance of thermodynamics to solving mathematical problems has recently spawned the field of thermodynamic computing15, leading to several hardware proposals14,16,17,18,19,20,21,22,23,24,25 including some with application to accelerating probabilistic AI14,16,17,21,22,23,24,25,26,27. Thermodynamic computing is based on the stochastic dynamics of a physical system acted on by a combination of conservative, dissipative, and fluctuating forces14,16,17. (In this article, we consider the case where the dynamical variables are continuous since continuous variables are relevant to generative AI methods such as diffusion models, Bayesian inference, which typically involves continuous probability distributions, and linear algebra.) These dynamics, called Langevin dynamics, can be modeled by the stochastic differential equations (SDEs):

$${{{\rm{d}}}}{{{\bf{x}}}}={M}^{-1}{{{\bf{p}}}}\,{{{\rm{d}}}}t$$
(1)
$${{{\rm{d}}}}{{{\bf{p}}}}=-\nabla U{{{\rm{d}}}}t-\gamma {M}^{-1}{{{\bf{p}}}}\,{{{\rm{d}}}}t+{{{\mathcal{N}}}}[0,2\gamma {\beta }^{-1}{\mathbb{I}}\,{{{\rm{d}}}}t],$$
(2)

where γ and β are positive real constants, and M may be either a positive real scalar or a positive definite matrix. (The noise term here is assumed to have a covariance matrix proportional to identity, i.e., the noise is uncorrelated, but in general, we may also replace the identity matrix with another positive definite matrix to model a system coupled to a correlated noise source16,17.) The vectors x and p represent (respectively) generalized coordinates describing the system’s state and their canonically conjugate momenta, and the function U(x) is the potential energy, which is responsible for conservative forces. The stationary distribution for x is called the Gibbs distribution

$$f({{{\bf{x}}}})=\frac{1}{Z}{e}^{-\beta U({{{\bf{x}}}})},$$
(3)

where the partition function Z is determined by normalization28. Thermodynamic computers allow U(x) to be (at least partially) programmable, which in turn allows the user to specify the distribution f(x) from which samples are drawn. Since noise is actually a desirable feature of the hardware, thermodynamic computers may have inherent robustness to noise14. Note that, since this approach relies on the Gibbs distribution, the system must be allowed to equilibrate before useful samples can be obtained. This time period is called the equilibration (or burn-in) time. Also, if two samples are drawn within a very small time interval, the values will be correlated. If uncorrelated samples are desired, the timescale one must wait is approximately set by the correlation time of the system. The equilibration and correlation times place important constraints on the performance of thermodynamic algorithms.

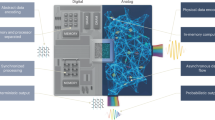
In this work, we present an experimental demonstration of thermodynamic computing. Our device is fabricated as a printed circuit board, with 8 fully connected unit cells. We employ this computer both as a sampling device, to sample from user-specified Gaussian distributions, and as a linear algebra device, to invert user-specified matrices. The latter represents an implementation of a thermodynamic linear algebra experiment. In the Supplementary Information, we also perform demonstrations on our hardware of important primitives in machine learning, including Spectral Normalized Neural Gaussian Processes29 for uncertainty quantification in neural networks (a method popular in Probabilistic AI30), linear regression, and Gaussian process regression31.

Our proof-of-principle demonstration highlights a future where thermodynamic advantage may be a reality, i.e., where thermodynamic computers outperform digital ones in either speed or energy efficiency. Indeed, asymptotic speedups have been theoretically predicted16,17, implying that there exists a threshold scale (or problem size) beyond which thermodynamic computers will outperform competition. Our numerical simulations presented herein suggest that this threshold scale is practically achievable. In order to maximize this advantage, it is necessary to investigate the space of possible designs and refine the architecture to facilitate large-scale CMOS implementation. Through our experiments, we have learned that our device’s specific architecture has scalability limitations, largely due to the use of inductors and transformers. These limitations are discussed, as well as possible refinements to our circuit design that will improve performance and ease of fabrication at scale. This work, therefore, represents material progress towards identifying an efficient and scalable silicon architecture for thermodynamic computing.

Results

The Stochastic Processing Unit

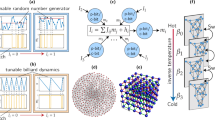
We now introduce our stochastic processing unit (SPU), which is depicted in the left panel of Fig. 1. The SPU is constructed on a Printed Circuit Board. From the lower left corner to the upper right corner, one can see the line of components corresponding to eight unit cells (LC circuits), while the components arranged in the triangle on the upper left correspond to the controllable couplings that couple the unit cells. We remark that we constructed three nominally identical copies of our SPU circuit, to test the scientific reproducibility of our experimental results.

Fig. 1: The stochastic processing unit (SPU).
figure 1

(Left panel) The Printed Circuit Board for our 8-cell SPU. (Right panel) Illustration of eight unit cells that are all-to-all coupled to each other, as in our SPU. Each cell contains an LC resonator and a Gaussian current noise source, as shown in the circuit diagram on the top right. The circuit diagram on the bottom depicts two capacitively coupled unit cells.

Full size image

The SPU can be mathematically modeled as a set of capacitively coupled ideal RLC circuits with noisy current driving. The diagram for this model is shown in the right panel of Fig. 1. Doing a simple circuit analysis reveals that the equations of motion for this circuit are

$${{{\rm{d}}}}{{{\bf{i}}}}={{{{\bf{L}}}}}^{-1}{{{\bf{v}}}}\,{{{\rm{d}}}}t$$
(4)
$${{{\rm{d}}}}{{{\bf{v}}}}=-{{{{\bf{C}}}}}^{-1}{{{{\bf{R}}}}}^{-1}{{{\bf{v}}}}\,{{{\rm{d}}}}t-{{{{\bf{C}}}}}^{-1}{{{\bf{i}}}}\,{{{\rm{d}}}}t+\sqrt{2{\kappa }_{0}}{{{{\bf{C}}}}}^{-1}{{{\mathcal{N}}}}[0,{\mathbb{I}}\,{{{\rm{d}}}}t],$$
(5)

where \({{{\bf{i}}}}={\left({I}_{L1},\ldots {I}_{Ld}\right)}^{{{{\rm{T}}}}}\) is the vector of inductor currents and \({{{\bf{v}}}}={\left({V}_{C1},\ldots {V}_{Cd}\right)}^{{{{\rm{T}}}}}\) is the vector of capacitor voltages. In the above, C is the Maxwell capacitance matrix, whose diagonal elements are \({{{{\bf{C}}}}}_{ii}={C}_{ii}+\mathop{\sum }_{j=1}^{d}{C}_{ij}\), and whose off-diagonal elements are Cij = −Cij. The values of resistors and inductors in each cell are represented by the matrices \({{{\bf{R}}}}=R{\mathbb{I}}\) and \({{{\bf{L}}}}=L{\mathbb{I}}\) respectively. Finally, \({{{\mathcal{N}}}}[0,{\mathbb{I}}\,{{{\rm{d}}}}t]\) represents a mean-zero normally distributed random displacement with covariance matrix \({\mathbb{I}}\,{{{\rm{d}}}}t\) and κ0 is the power spectral density of the current noise source. In this implementation, in order for the noise amplitude to be of sufficient magnitude, the noise source is a controllable random bit stream generated by a digital controller (see Supplementary Information for more details). If the magnitude of the noisy driving current is larger than the intrinsic noise in the system, then κ0 can be thought of as an effective temperature control for thermodynamic computation.

Equations (4) and (5) can be mapped to the Langevin equations (1) and (2) by making a change of coordinates. Specifically, we introduce the magnetic flux vector ϕ and the Maxwell charge vector q, defined as

$${{{\boldsymbol{\phi }}}}=L{{{\bf{i}}}},\quad {{{\bf{q}}}}={{{\bf{C}}}}{{{\bf{v}}}}.$$
(6)

As shown in the Supplementary Information, ϕ and q are canonically conjugate coordinates, with ϕ playing the role of position and q playing the role of momentum. We also introduce an effective inverse temperature parameter \(\beta=\gamma {\kappa }_{0}^{-1}\). In terms of these variables, Eqs. (4) and (5) become

$${{{\rm{d}}}}{{{\boldsymbol{\phi }}}}={{{{\bf{C}}}}}^{-1}{{{\bf{q}}}}\,{{{\rm{d}}}}t$$
(7)
$${{{\rm{d}}}}{{{\bf{q}}}}=-{L}^{-1}{{{\boldsymbol{\phi }}}}\,{{{\rm{d}}}}t-{R}^{-1}{{{{\bf{C}}}}}^{-1}{{{\bf{q}}}}\,{{{\rm{d}}}}t+{{{\mathcal{N}}}}[0,2{R}^{-1}{\beta }^{-1}{\mathbb{I}}\,{{{\rm{d}}}}t].$$
(8)

It is clear that Eqs. (7) and (8) are equivalent to (1) and (2) when we make the identifications x = ϕ, p = q, M = C, γ = R−1, and \(U({{{\bf{x}}}})=U\left({{{\boldsymbol{\phi }}}}\right)=\frac{1}{2}{{{{\boldsymbol{\phi }}}}}^{T}{{{{\bf{L}}}}}^{-1}{{{\boldsymbol{\phi }}}}\). In these coordinates, the Hamiltonian, without noise or dissipation, of the system is expressed as

$${{{\mathcal{H}}}}\left({{{\boldsymbol{\phi }}}},{{{\bf{q}}}}\right)=\frac{1}{2}{{{{\boldsymbol{\phi }}}}}^{T}{{{{\bf{L}}}}}^{-1}{{{\boldsymbol{\phi }}}}+\frac{1}{2}{{{{\bf{q}}}}}^{T}{{{{\bf{C}}}}}^{-1}{{{\bf{q}}}},$$
(9)

and consequently, the stationary distribution of Eqs. (7) and (8) is the Gibbs distribution given by

$${{{\boldsymbol{\phi }}}} \sim {{{\mathcal{N}}}}[0,{\beta }^{-1}{{{\bf{L}}}}],\quad {{{\bf{q}}}} \sim {{{\mathcal{N}}}}[0,{\beta }^{-1}{{{\bf{C}}}}],$$
(10)

where ϕ and q are independent of each other.

The time to reach the Gibbs distribution, the equilibration time, is closely related to the correlation time τcorr, since equilibration can be interpreted as the decorrelation of the system from its initial state. So the two timescales are essentially the same. While sampling at a rate given by the inverse correlation time of the system is a guarantee of uncorrelated samples, in practice, one can sample much faster and retain good performance, see Supplementary Information for details. For our SPU, the correlation function decays exponentially with a time constant of approximately

$${\tau }_{{{{\rm{corr}}}}}\approx R{c}_{\max },$$
(11)

where \({c}_{\max }\) is the largest eigenvalue of C (see, e.g., ref. 16). (There are some minor corrections involving the other circuit parameters, but these have relatively little effect.) In order for the correlation function to decay to less than one percent of its original magnitude, we may wait for an interval of at least 5τcorr, for example. If one periodically measures the voltages, v, across the capacitors after the device has reached equilibrium, one finds that the voltage samples will have a covariance matrix of

$${{{{\mathbf{\Sigma }}}}}_{{{{\bf{v}}}}}=R{\kappa }_{0}{{{{\bf{C}}}}}^{-1}.$$
(12)

We now describe how this computing system can be used for various mathematical primitives.

Gaussian sampling

Let us describe how to perform Gaussian sampling with our thermodynamic computer. Consider a zero mean multivariate Gaussian distribution (since we can always translate the samples by a constant vector to generate a non-zero mean):

$${{{\mathcal{N}}}}({{{\bf{x}}}}| {{{\mathbf{\Sigma }}}})=\frac{1}{\sqrt{{(2\pi )}^{N}| {{{\mathbf{\Sigma }}}}| }}\exp \left(-\frac{1}{2}{{{{\bf{x}}}}}^{T}{{{{\mathbf{\Sigma }}}}}^{-1}{{{\bf{x}}}}\right),$$
(13)

where Σ is the covariance matrix. Here, we consider the case where the user provides the precision matrix P = Σ−1 associated with the desired Gaussian distribution (See Supplementary Information for the alternative case where the user provides the covariance matrix Σ.)

As described above, the stationary distribution of the voltages and currents in the SPU is dependent on the noise- and dissipation-free Hamiltonian of the circuit. The Hamiltonian for the coupled oscillator system (see Supplementary Information for details) is given by:

$${{{\mathcal{H}}}}\left({{{\bf{i}}}},{{{\bf{v}}}}\right)=\frac{1}{2}{{{{\bf{v}}}}}^{T}{{{\bf{C}}}}{{{\bf{v}}}}+\frac{1}{2}{{{{\bf{i}}}}}^{T}{{{\bf{L}}}}{{{\bf{i}}}},$$
(14)

where i is the vector of currents through the inductors in each unit cell, v is the vector of voltages across the capacitors in each unit cell, C is the Maxwell capacitance matrix, and L is the inductance matrix.

At thermal equilibrium, the dynamical variables are distributed according to a Boltzmann distribution, proportional to \(\exp (-{{{\mathcal{H}}}}/kT)\), and hence v is normally distributed according to:

$${{{\bf{v}}}} \sim {{{\mathcal{N}}}}[{{{\bf{0}}}},kT{{{{\bf{C}}}}}^{-1}]$$
(15)

Thus, if the user specifies the precision matrix P, then we can obtain the correct distribution for v by choosing the Maxwell capacitance matrix to be:

$${{{\bf{C}}}}=kT{{{\bf{P}}}}$$
(16)

Hence, this describes how we can map the user-specified matrix to the matrix of electrical component values, to obtain the desired distribution.

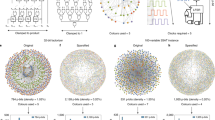
Figure 2 is a visualization of a Gaussian sampling experiment performed on our SPU (here, the data from two unit cells is reported, see the Supplementary Information for the rest of the results). One can see good agreement with the theoretical distribution and its marginals. One can also see that the the error associated with the moments of the distribution goes down over time as more samples are gathered.

Fig. 2: Sampling a two-dimensional Gaussian distribution on the SPU.
figure 2

Measurements of the voltages of two coupled cells of the SPU were taken at a rate of 12 MHz. Top Left: histogram of the marginal of cell i. Top right: Absolute error between the target covariance matrix and the device covariance matrix (abbreviated as Cov.), similarly for the skewness and kurtosis (respectively abbreviated as Skew. and Kurt.), all calculated using the Frobenius norm. Bottom Left: Scatter plot of voltage samples from both cells. Bottom Right: Histogram of the marginal of cell j. For the marginal plots, the theoretical target marginal is overlaid as a solid red curve. Similarly, for the two-dimensional plot, the theoretical curve corresponding to two standard deviations from the mean is overlaid as a solid red curve. Source data are provided as a Source Data file.

Full size image

Matrix inversion

The second primitive we will consider is matrix inversion, which was discussed in the context of thermodynamic computing in ref. 16. Following that reference, we envision the user encoding their matrix A in the precision matrix P of the associated Gaussian distribution that will be sampled. Hence from Eq. (16), the Maxwell capacitance matrix of the hardware is given by C = kTA. Choosing this Maxwell capacitance matrix, we find from Eq. (15) that at thermal equilibrium, the voltage vector is distributed according to

$${{{\bf{v}}}} \sim {{{\mathcal{N}}}}[{{{\bf{0}}}},{{{{\bf{A}}}}}^{-1}]$$
(17)

Therefore, we can invert matrix A simply by collecting voltage samples at thermal equilibrium and computing the sample covariance matrix. (This assumes that A is a positive semi-definite (PSD) matrix, although the extension to non-PSD matrices is possible with a pre-processing step16).

Figure 3 shows the 8 × 8 matrix inversion results. We perform the algorithm on three distinct copies of the SPU, which are nominally identical (although may slightly differ due to component tolerances). The fact that similar results are obtained on all three SPUs, as shown in Fig. 3A, is useful for demonstrating scientific reproducibility. Indeed, one can see the error (i.e., the relative Frobenius error between the SPU inverse and the target inverse) goes down as the number of samples increases. The SPU inverse, after gathering several thousand samples, looks visually similar to the target inverse. Moreover, Fig. 3B shows the time evolution of the SPU inverse. One can see in Fig. 3B that the SPU inverse gradually looks more-and-more like the true inverse as more samples are gathered.

Fig. 3: Thermodynamic inversion of an 8 × 8 matrix.
figure 3

This experiment was performed independently on three distinct (but nominally identical) copies of the SPU. A The input matrix A and its true inverse A−1 are shown, respectively, in the first and second panel. The relative Frobenius error versus the number of samples is plotted in the third panel, for each of the three SPUs. The three panels on the right show the experimentally determined inverses after gathering 12,000 samples on each of the three SPUs. B The time progression of thermodynamic matrix inversion is shown. From left to right, more samples are gathered from the SPU to compute the matrix inversion. The number of samples and the inversion error are stated below each panel. One can visually see the resulting inverse look more like the target inverse as more samples are obtained. Source data are provided as a Source Data file.

Full size image

The fact that the error does not go exactly to zero indicates that experimental imperfections are present. This likely includes capacitance tolerances (i.e., nominal capacitance values being off from their true values) and imprecision. We recently showed that the latter can be addressed with a judicious averaging protocol, and the experimental error for matrix inversion can be significantly reduced32. Thus, imprecision-based errors can be mitigated for this system.

In the Supplementary Information, we show some additional plots for matrix inversion on our SPU, including the dependence of the error on the condition number of A and on the smallest eigenvalue of A.

Performance advantage at scale

We now focus on the potential advantage that one could obtain from scaling up our SPU. Specifically, we compare the expected runtime and energy consumption of our SPU to that of state-of-the-art GPUs. Our mathematical model for runtime and energy consumption involves considering the effect of three key stages:

  1. 1.

    Calculating the component values of the capacitor array from the input covariance matrix (digital calculation, on a GPU)

  2. 2.

    Loading the component values to the device (digital transfer)

  3. 3.

    Waiting for the integration time of the physical dynamics needed to generate the samples (analog runtime).

  4. 4.

    Sending the samples back to the digital device through an ADC.

We assume the SPU is constructed from standard electrical components operating at room temperature and the ideal case of electrical components with 16 bits of precision, as well as that the SPU units are fully connected (This analysis is valid whether the user provides the covariance matrix or the precision matrix, where details of sampling when the covariance matrix is provided is discussed in Supplementary Information.) We assume the following:

  • The physical time constant of the system is 1μs.

  • The number of ADC channels scales with dimension, with a sampling rate of 10 Megasamples per second.

  • The power per cell is 0.005 mW, dominated by ADC power consumption.

For comparison with digital state-of-the-art, we obtain digital timing and energy consumption results using a JAX implementation of Cholesky sampling on an NVIDIA RTX A6000 GPU using the package zeus - ml33.

Figure 4a  shows how the time taken to produce samples from a multivariate Gaussian scales with dimension, for the cases of drawing 1 sample and drawing 10,000 samples. We emphasize that this figure is relevant to both Gaussian sampling and matrix inversion, because one can always use the obtained samples to estimate the matrix inverse. Hence, the timing results shown in this figure apply to both Gaussian sampling and matrix inversion.

Fig. 4: Comparison of GPU and estimated SPU performance.
figure 4

a Time to solution to obtain Gaussian samples for dimensions ranging from 100 to 10,000 for an A6000 GPU (black squares) and estimated for the SPU (red dots), for both a single sample (dashed lines) and 10,000 samples (solid lines). b Corresponding energy to solution, directly measured for the GPU and estimated for the SPU. Source data are provided as a Source Data file.

Full size image

One can see that for 10,000 samples, the GPU is faster for low dimensions, but the SPU performance is expected to outperform the GPU for high dimensions. The cross-over point, which we call the point of “thermodynamic advantage”, occurs around d = 3000 for the assumptions we made. The asymptotic scaling for high dimensions is expected to go as O(d2) for the SPU, as opposed to O(d3) for Cholesky sampling on the GPU. At d = 10,000, an order-of-magnitude speedup is predicted, and larger speedups could be unlocked by scaling up the system to larger sizes.

For the case of drawing a single sample, we once again predict roughly an order-of-magnitude speedup for the SPU over GPUs at d = 10,000. However, what is different about this case is that a speedup is predicted over the entire range of dimensions considered, with a small speedup even being predicted at low dimensions (e.g., d = 100). The large difference in SPU runtime (between the single sample and 10,000 sample cases) is because the runtime is dominated by the ADC conversion, which is greatly reduced in the case of a single sample.

It is also of interest to consider energy, since it is well known that GPUs consume large amounts of energy. In contrast, the natural dynamics of a physical system are energy-frugal and could reduce the expected energy requirements. Figure 4b shows how the energy of generating Gaussian samples is expected to scale with dimension for both the SPU and GPU. (Note that a large variance is observed for energy because of the direct measurement of GPU operations for both the GPU and SPU benchmarks.) One can see that our model predicts the exciting prospect that the SPU provides energy savings for all dimensions, even for low dimensions. Moreover, the energy savings is an order of magnitude at d = 10,000 and is expected to continue to grow for larger dimensions.

It is encouraging that a simple model of the SPU, the timings involved in its end-to-end operation, and the energy cost during these processes lead to a potential speedup and energy savings of more than an order-of-magnitude relative to state-of-the-art GPUs with relatively conservative assumptions. Nevertheless, these results represent a mathematical model, and the true evidence of thermodynamic advantage will only be obtained by directly scaling up the SPU hardware.

A scalable architecture

An important lesson learned from the small-scale proof-of-concept experiments reported above is that the architecture we employed would not be the best choice for a large-scale implementation that would require miniaturization as an integrated circuit (IC). Firstly, the presence of inductors and transformers makes an IC implementation very difficult due to, e.g., the physical size of the inductors and their relatively strong parasitic coupling and crosstalk at those scales34,35. Secondly, area constraints on an IC would likely require the capacitances to be very small (particularly for high dimensions), leading to a very short RC time constant. Therefore, the noise must have a very large bandwidth to match the timescale of the system’s dynamics.

We propose here an alternative architecture that is better suited to overcome these issues of large-scale implementation. The proposed architecture uses RC unit cells and resistive coupling and is shown as a 2-dimensional example in Fig. 5a. A detailed analysis of the dynamical equation for this circuit is given in the Supplementary Information. Clearly, this architecture eliminates scaling issues related to inductors. Moreover, our numerical benchmarks of this architecture (provided in the Supplementary Information) involving a mathematical model for runtime and energy consumption show a similar speedup and energy advantage as that shown in Fig. 4. Hence, the advantage can be preserved while switching to a more scalable architecture.

Fig. 5: Architecture with resistive coupling.
figure 5

a Circuit diagram for two unit cells of the proposed architecture with resistive coupling. b SPICE simulations of matrix inversion for d = 25 with this architecture, showing qualitative agreement between the target and the experimentally determined inverse. c For this SPICE simulation, the relative error is plotted versus the number of samples. d CADENCE simulations for d = 20 unit cells with the resistively coupled architecture are shown, plotting the relative error versus time. The three curves correspond to the case where all components are ideal and have the exact value needed (orange), the case where all components are ideal, but where the resistances are composed of 8-bit banks of resistors (red), and the case where all the components are simulated with non-idealities given by the fabrication models (green) and the resistances are composed of 8-bit banks. Source data are provided as a Source Data file.

Full size image

We further confirm the performance of this circuit by running SPICE simulations shown in Fig. 5b. In this simulation, 25 unit cells are densely connected by an array of resistors to calculate the inverse of a 25 × 25 matrix. Figure 5c shows the relative error of the inverse matrix calculated by the circuit simulation and the target inverse as a function of the number of voltage measurements. We can see that this circuit behaves as expected, and the stationary distribution is indeed a normal distribution with covariance equal to the inverse of the conductance matrix.

To account for the impact of non-idealities, we ran Cadence simulations, shown in Fig. 5d. This simulation, for d = 20 unit cells, fully accounts for realistic hardware components using component models from the fabrication foundry as well as quantization error by implementing the tunable resistances (conductances) as banks of multiple resistors that can be individually addressed. The green curve in this plot represents the most realistic case where all the components have real models and all coupling elements are implemented using 8-bit resistor banks. The asymptotic error is still reasonable (~2%) despite accounting for non-idealities, suggesting that this architecture has the potential to perform well in a realistic setting. This study of fabrication-based non-idealities reveals that fabrication defects are not dominant compared to the quantization error. We remark that this provides hope for employing quantization-based error mitigation methods32 to reduce overall error. Finally, in the Methods section, we provide detailed timing and energy benchmarks from our Cadence simulations as a function of dimension, showing how the energy costs, runtime, and area on chip increase with dimension.

Discussion

In this work, we presented a thermodynamic computing prototype that we used to demonstrate a thermodynamic linear algebra experiment (among other experiments). We identified key challenges in scaling up this hardware, motivating us to propose a slightly modified architecture that does not employ inductors and uses resistive (instead of capacitive) coupling. Nevertheless, there still remain some additional challenges in scaling this hardware. For example, the accuracy of thermodynamic computation is limited by the precision with which physical parameters are specified, and inevitably there is a tradeoff between precision and scalability. In recent work, we have proposed (and experimentally implemented) a strategy to increase the accuracy that can be achieved on a low-precision device32, and this method effectively boosts the precision of the hardware by several bits. Given that imprecision-based error appears to dominate in our simulations in Fig. 5 (e.g., relative to error associated with component tolerance), the error mitigation strategy of ref. 32 looks promising.

Another challenge for thermodynamic computing at a large scale is producing a device with the necessary connectivity requirements. In this work, we presented a fully connected design, and it will be more difficult to build a circuit with \({{{\mathcal{O}}}}\)(1000) or greater nodes while being fully connected. Fortunately, full connectivity is not needed for all applications, for example, ref. 36 presents an algorithm that relies on a low-rank factorization allowing for reduced connectivity requirements.

In addition to the challenges above, this work also brings into focus several opportunities. While we have only discussed Gaussian sampling and matrix inversion in this work, it has been shown that hardware similar to the device presented here can be used to accelerate other tasks such as solving a linear system16, computing a matrix exponential17, and second-order optimization36. Further modification of the device would allow for sampling from non-Gaussian distributions14, and it has been shown that using transistors to introduce non-linearities would allow for efficiently sampling the Bayesian posterior of a logistic regression model37. Having performed an experimental demonstration of thermodynamic computing in the Gaussian case, we have provided guidance for future experimental work in the non-Gaussian case, which could unlock generative AI applications like diffusion models38.

The field of thermodynamic computing is in its early days, analogous to when small-scale quantum computers were built in the 1990’s39. Just as quantum computing was driven by the promise of accelerating a key application, namely factoring40, thermodynamic computing may be driven by its promise to make AI more efficient. However, while thermodynamic computing has the challenges noted above (precision and connectivity), it does not share the more severe scalability issues of quantum computing like isolation from the environment (i.e., decoherence), cryogenic temperatures, thermal noise, unconventional fabrication, and non-CMOS materials engineering41. Thus, the lack of technological barriers for thermodynamic computing can potentially make it a more near-term alternative to quantum computing for primitives like linear algebra and sampling from user-specified distributions.

These primitives often appear in probabilistic AI algorithms, and it is well known that probabilistic AI is computationally challenging on current digital hardware12. Yet probabilistic AI is crucial to unlocking reliable AI for high-stakes (i.e., risk-averse) applications since standard (non-probabilistic) AI technology is not proficient at essential tasks such as quantifying uncertainty of predictions42. Thus, thermodynamic computing may play a key role in enabling AI systems that can reason in uncertain, high-stakes situations.

Methods

Here we provide additional details on the design of our hardware, including the coupled resonator structure, the interface to digital hardware, and the readout process. Further details (e.g., discussion of the noise source) can be found in the Supplementary Information.

Coupled resonators structure

While Fig. 1 shows a high-level view of the circuit structure, we give a more precise depiction in Fig. 6A. (For simplicity, we only show two unit cells in Fig. 6, even though our SPU has 8 cells.) Each cell consists of an inductor, a tunable capacitor, and a current noise source that is uncorrelated to other noise sources in the SPU. While ideally, a continuously tunable capacitor is desired, available technologies (e.g., varactor diodes or BST-based varactors) typically suffer from nonlinearity or complexity of integration. Consequently, we use switched capacitors in a capacitor bank. Simulations show that, with as little as three capacitors, the quality of operation is nearly unaffected. The exact values of the capacitors were chosen with numerical optimization to obtain the best performance.

Fig. 6: Structure of the thermodynamic computing system.
figure 6

A simplified version of the SPU, containing two cells with a single coupling branch, is shown in (A). In-cell capacitances arise from a bank of three capacitors, as shown. The coupling capacitance arises from a single-switched capacitor. A transformer appears in the coupling circuit, for the purpose of achieving bipolar coupling. The interface of the SPU with digital hardware is shown in (B) and (C). The SPU is controlled by a digital device as a co-processor. B shows the back of the circuit board, displaying both the FPGA and the USB that leads to the CPU. C Shows schematically how the data flows between the analog and the digital devices. The data that determines the circuit parameters is downloaded from the CPU to the SPU, and the sampling data is uploaded from the SPU to the CPU. The FPGA acts as an intermediary in this process and also provides the noise source.

Full size image

The coupling between the resonators is implemented capacitively. Similar to the capacitors in the cells, the coupling capacitors should ideally be continuously controlled, but a switched capacitor is used due to the limitations of tunable capacitors. A center-tapped transformer is used to switch between positive and negative polarity coupling, which allows one to achieve bipolar coupling. The nominal capacitances for the in-cell capacitors are chosen from the following set of values:

$$\, {{\mbox{In}}}- {{\mbox{cell}}} \,{{\mbox{capacitances}}}\,\,\in \{1.0 {{\mbox{nF}}},3.2 {{\mbox{nF}}},4.3 {{\mbox{nF}}},6.5 {{\mbox{nF}}} \}.$$

The nominal coupling capacitance is 0.47 nF through a center-tapped transformer, making the available coupling values:

$$\, {{\mbox{Coupling}}} \, {{\mbox{values}}}\,\,\in \{ {{\mbox{-x}}},0,{{\mbox{x}}} \}.$$

where x = 0.47 × 10−9. The inductors used in each unit cell have values of 2.2 μH (part num. XAL7020-222), while the transformers used in the couplings are the WBC2-1TL.

Interface to digital hardware

Figure 6 also shows the interface between the analog and digital hardware for our thermodynamic computing system. Broadly speaking, our SPU functions as a co-processor to a digital device. Namely, the operation of the SPU is controlled by a Central Processing Unit (CPU) and a Field-Programmable Gate Array (FPGA). Figure 6B shows the back of the circuit board for the SPU. One can see the FPGA attached to the board as well as the Universal Serial Bus (USB) that leads to the CPU. The CPU compiles the requested covariance matrix into FPGA code, while the FPGA opens and closes the switches controlling the capacitance values and the coupling branches and also starts the noise sources, as shown in Fig. 6C. The FPGA then starts the measurement phase where voltage measurements are taken at a given rate, then digitized by an onboard analog-to-digital converter (ADC) and sent to the CPU.

Readout of samples

Reading the voltage across each cell occurs after the capacitance values are set, and the noise source is initiated. In order to collect a sufficiently large number of samples to be statistically significant, the sampling rate is expected to be relatively high. On the other hand, a high sampling rate might result in a non-zero correlation between a sample and a subsequent one. The time until samples become uncorrelated is inversely proportional to the quality factor (Q) of the LC resonators. For this implementation, the optimal sampling rate was found to be 12 MHz, using an eight-channel 10-bit ADS5292 ADC.

Predicted IC scaling

Simulations were performed using CADENCE for the architecture with resistive coupling shown in Fig. 5 applied to the matrix inversion task. Non-idealities were accounted for in these simulations by using the realistic device models provided by fabricators and by implementing tunable components as 8-bit banks of components. Performance predictions were extracted from these simulations and are reported in Table 1. The first row shows the predicted area occupied on a silicon chip, the second row shows the final relative error achieved, the third and fourth rows show the power consumption without and with accounting for ADCs (respectively), the fifth and sixth rows show the energy required to reach 10% error without and with accounting for ADCs (respectively), and the final row shows the runtime required to reach 10% error.

Table 1 Simulated integrated circuit parameters and performance as a function of dimension
Full size table