Main

In the realm of condensed-matter physics, the exploration of novel phases of matter is a cornerstone of scientific investigation. Our understanding of correlated electronic states, including superconductors, magnetic materials and topological phases, has greatly benefited from key principles such as spontaneous symmetry breaking, Berry phase and topology1,2,3,4,5. These phenomena underpin emerging technologies owing to their remarkable properties and potential applications6,7. To comprehend complex systems with multiple degrees of freedom, gaining insights into the symmetries and electronic properties of materials is crucial. Chirality is a pervasive phenomenon in the natural world, from biomolecules to condensed-matter physics8,9,10,11,12, and is a fundamental manifestation of symmetry breaking. In particular, it denotes the absence of mirror planes, spatial inversion centres or rotational inversion axes in a crystalline arrangement. Its impact extends across diverse domains, including molecular biology, medicine and pharmaceuticals, making it a subject of profound interest1. Here we investigate the interplay between chirality and electron spin in few-layer semiconductors, focusing on indium selenide (InSe). This material is chosen for its reliable fabrication, reproducibility, and clear optical and electrical signatures related to the Van Hove singularity at the valence band maximum (VBM)13,14,15,16,17,18. Few-layer InSe, with its remarkable electrical conductivity and bandgap, which is tunable through layer engineering, is an ideal platform for exploring emergent phenomena by manipulating specific symmetries13,15,16,19,20,21,22. Our study centres on the out-of-plane tunnelling current in InSe-based field-effect devices. We observe a magnetic-field-dependent tunnelling current associated with the Van Hove singularity, exhibiting symmetric behaviour under linearly polarized light excitation and asymmetric response under circularly polarized light. Interestingly, the superposition of these two electrical responses under opposite light chiralities reproduces the one measured under linearly polarized excitation.

Our findings demonstrate the ability to electrically detect the chirality of light by selectively exciting the sample with different light polarizations and maintaining a fixed magnetic field. This observation is explained by the presence of uncompensated Zeeman splitting in the spin bands of the InSe VBM and the hexagonal boron nitride (hBN) barrier. Our first-principles calculations reveal a quenching of the g-factor of holes at the VBM in InSe, allowing the hBN g-factor to remain uncompensated under the applied magnetic fields. These results enable us to determine the hole g-factors of both hBN and InSe for various devices and InSe layer numbers, consistent with our calculations.

With a remarkable minimum-detectable energy barrier change of approximately 15 μeV at 100 mK, our approach offers a fresh perspective on exploring the interplay between chirality and spin in the field of material physics at the thermal limit.

Device structure and tunnelling currents in few-layer InSe

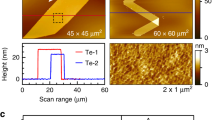
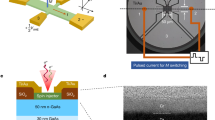
To achieve high-quality samples, we encapsulate few-layer γ-phase InSe in hBN and use few-layer graphite (FLG) as the electrode. We use an FLG bottom gate to control the carrier density in the semiconductor23. The complete device schematic is shown in Fig. 1a, illustrating an InSe-based heterostructure optically stimulated by laser light of different chiralities. To further confirm our device geometry, we performed a cross-sectional scanning transmission electron microscopy characterization (Supplementary Note 9). Figure 1b shows the electrical transport characteristic of a representative InSe device, showing ambipolar conduction with a dominant n-type current. The tunnelling current measured between the InSe channel and the FLG back gate is shown in blue and will be the main subject of this work. Figure 1c displays a scanning map of the out-of-plane photocurrent, displaying a robust signal that is uniform across the clean areas of the InSe flake and suppressed in the FLG electrodes or outside the semiconductor region. As discussed in our previous work14, the tunnelling current can be analysed following the Simmons approximation, providing information about the energy barrier height and the flat-band energy position24,25.

Fig. 1: Schematic and characterization of an encapsulated InSe device.
figure 1

a, Three-dimensional schematic representing an hBN-encapsulated InSe layer with FLG contacts and an FLG back gate (Gr gate). The sample is optically excited using a 532 nm laser with different chiralities. b, Electrical characterization of an exemplary 5L InSe device, showing ambipolar transport (red) and an increase in tunnelling current (blue) when the Fermi level reaches the Van Hove singularity, labelled as VTRAN. c, Optical micrograph of our device, superimposed on the scanning tunnelling current spatial map, highlighting that the signal is observed only when the laser spot is located on the InSe flake. In particular, the signal disappears when shining on the FLG electrodes (grey), or outside of the semiconductor area. The electrical measurement scheme is shown at the bottom. d, Normalized differential tunnelling conductance (red) shows the trend of the density of states in our device under study. The signal is obtained from the out-of-plane tunnelling current within the device, as discussed in our previous work14. The Van Hove singularity is clearly visible as a peak in conductance. The tunnelling current shown in blue is plotted to highlight the trend of the tunnelling mechanism. The linear region corresponds to the Fowler–Nordheim tunnelling regime, whereas the logarithmic trend corresponds to the direct tunnelling regime, as investigated previously14. The tunnelling energy barrier height can be extracted by fitting the linear regime. The gate voltage corresponding to the valence band is highlighted by the grey dashed line labelled as VTRAN.

Full size image

Magnetic field dependence of tunnelling currents

After determining the flat-band position, we apply various gate voltages corresponding to Fermi-level positions within the conduction band (CB) (Vg = 1 V), the bandgap Vg = −3 V and at the VBM (Vg = −6 V). Subsequently, we record the out-of-plane magnetic field dependence of the tunnelling photocurrent intensity under linearly polarized light excitation. Our findings (Fig. 2a) show a constant signal when the Fermi level resides within the CB (Vg = 1 V) or within the bandgap (Vg = −3 V). Conversely, as the Fermi level approaches the VBM (Vg = −6 V), we observe a symmetric increase in signal intensity for both magnetic field polarities. The absence of magnetic field dependence in the first two cases can be attributed to the high energy barrier experienced by the charge carriers, corresponding to the difference between the CBs of InSe and hBN (~3 eV). This results in a vanishingly small tunnelling signal, preventing any detectable response to magnetic field changes (Supplementary Note 2). However, as the Fermi level reaches the VBM of InSe, the tunnelling current grows exponentially with an increasing magnetic field strength. From the formalism that describes tunnelling currents in our system14, we can understand that once the device geometry is established, at a given gate voltage, a change in tunnelling current must be related to a change in the energy barrier height, which affects the magnitude in an exponential manner, as shown by the equation \({I}_{{{\rm{FNT}}}}\propto \frac{{V}_{{\it{G}}}^{2}}{{{{\phi }}}_{{\it{B}}}}\exp \left[\frac{{-{{\phi }}}_{{\it{B}}}^{3/2}}{{{\it{V}}}_{{\it{G}}}}\right]\). This phenomenon suggests a linear dependence between the applied magnetic field along the \(\hat{z}\) direction and a change in the energy barrier height, consistent with the Zeeman effect on which we elaborate below.

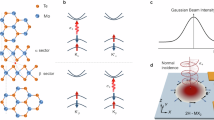
Fig. 2: Magnetic field dependence of tunnelling currents in few-layer InSe.
figure 2

a, Magnetic-field-dependent tunnelling current is shown at different gate voltages corresponding to different charge configurations: within the CB (Vg = 1 V), bandgap region (Vg = –3 V) and valence band (Vg = –6 V). The signal recorded at the valence band energy shows a symmetric increase for both magnetic field polarities, whereas no modulation is observed in the other cases. The signal is recorded under linearly polarized light excitation, at a laser power of 150 μW. b, Valence band structure calculated for 3L γ-InSe. 3L is used for our computations since it shows qualitatively analogous results with respect to 5L, and it requires a simpler computation. The linecuts are shown for two different directions in the Brillouin zone. The solid and dashed lines represent two different spin configurations. The linecuts exhibit the same spin sub-band at higher energies. However, when we consider the Brillouin zone, we observe that three valleys have a higher energy for one spin configuration, whereas the other three valleys favour the other spin configuration. c, Band structure of multilayer hBN. d, Calculated change in the energy barrier as a function of the magnetic field. The increase in tunnelling current (as shown in a) can be translated into an energy barrier change that is proportional to the Zeeman splitting of the energy bands involved. From this measurement, we can extract a total g-factor of around 2 for both magnetic field polarities, which is consistent with our calculations for InSe and hBN. The insets show the energy barrier height at B = 0 \({({\phi }_{{\it{B}}_0})}\), and at higher fields, with the Zeeman splitting contribution Ez. e, First-principles calculations of angular momenta for 3L InSe. The spin (Sz) and orbital (Lz) components are calculated for the band structure shown in b, and the total out-of-plane g-factor is shown. In particular, at the VBM position, both spin and orbital components are suppressed, indicating that the spins are oriented in plane. This result holds for all InSe multilayers. The VBM neighbouring points possess a non-vanishing g-factor, which will be relevant, as displayed in the power dependence measurements. f, Angular momenta computed for the hBN valence band. Here the orbital contribution is vanishingly small across the area of interest in the Brillouin zone, and the total contribution to the out-of-plane g-factor comes from the spin component. Overall, along the out-of-plane direction, only hBN is dominant for a change in energy barrier height, since the holes in InSe relax to the VBM before tunnelling, which possesses a quenched g-factor.

Full size image

To understand the origin of this effect, we have conducted first-principles calculations to determine the total out-of-plane g-factors of valence band carriers in InSe and hBN along important high-symmetry directions of the Brillouin zone. Our calculations include both spin (Sz) and orbital (Lz) components to the band g-factor (gz = Sz + Lz; Supplementary Note 3). Although a strong spin polarization was previously calculated for monolayer InSe for the out-of-plane direction26, this feature is strongly suppressed in multilayer γ-InSe (Supplementary Note 3). Our calculations reveal a quenching of the g-factor at the VBM, both for the spin and orbital counterparts (Fig. 2e). This result suggests that the carrier spins at the VBM are oriented in the in-plane direction and that the energy band edges are, therefore, nearly insensitive to an applied magnetic field B. This is a rather unique feature among semiconductors and other known materials27,28,29,30. The origin of this is the broken mirror-plane symmetry, which gives rise to the Bychkov–Rashba effect31, accompanied by a suppression of spin and angular momenta in the out-of-plane directions32. To further confirm the validity of our first-principles calculations, we determine an exciton (ΓCB – ΓVB) g-factor of 0.22, in excellent agreement with the previous33 experimental value (0.18).

In the presence of a magnetic field, the barrier height is defined by the energy difference between the VBMs of InSe and hBN (ref. 14), since the signal originates at the VBM of InSe (ref. 14). Importantly, the graphite layer serves as the final state for the tunnelling carriers. As long as the Fermi level of graphite is above the valence band edge of InSe, it does not introduce an additional barrier for the hole-tunnelling process. For this reason, FLG gates are preferred with respect to monolayer graphene, and the magnetic field dependence of the final state is not considered relevant at this stage. Owing to the negligible gz value of carriers at the VBM of InSe, it does not shift with the field. However, the hBN spin bands at the VBM shift with a g-factor of ~|1| and a negligible orbital contribution (Fig. 2c–f and Supplementary Note 3). Since the observed tunnelling current changes exponentially with the energy barrier height, a modest change in the energy barrier can produce a detectable change in tunnelling current (Fig. 2a). In particular, when a positive (negative) magnetic field is applied, the spin-up (spin-down) band of the hBN VBM will shift upwards in energy, whereas the spin-down (spin-up) band will shift downwards. As a result, the energy barrier height will decrease by an amount equal to the Zeeman energy splitting for the spin-up (spin-down) band and increase for the spin-down (spin-up) band by the same quantity (Fig. 2d shows the band diagrams). The tunnelling current at the VBM of InSe follows the Fowler–Nordheim formalism14,24,34 (Supplementary Note 4). By comparing the signal at Bz = 0 with the one at higher fields, we can extract the energy barrier change considering both spin band energy changes by using the following system of equations:

$$\log \left[{I}_{\downarrow }/{I}_{\uparrow }\right]=\,\log \left[\frac{{\phi }_{B_0}-{\Delta {\it{E}}}_{{\it{B}}}}{{\phi }_{B_0}+{\Delta {\it{E}}}_{{\it{B}}}}\right]+{\rm{\gamma }}{({\phi }_{{\it{B}}_0}+{\Delta {\it{E}}}_{{\it{B}}})}^{\frac{3}{2}}-{\rm{\gamma }}{({\phi }_{{\it{B}}_0}-{\Delta {\it{E}}}_{{\it{B}}})}^{\frac{3}{2}},$$
$$\log \left[{I}_{\downarrow }/{I}_{0}\right]=-{\rm{\gamma }}({\phi }_{{\it{B}}_0}^{\frac{3}{2}}-{({\phi }_{{\it{B}}_0}+{\Delta {\it{E}}}_{{\it{B}}})}^{\frac{3}{2}}),$$

where \({{\phi }_{{\it{B}}_0}}\) is the energy barrier height at Bz = 0 and \({\rm{\gamma }}=\frac{-8{{\uppi }}\sqrt{{2m}^{* }}{{d}}}{3{{hq}}{{{V}}}_{{\it{G}}}}\). The currents I↑,↓ originate from the bands moving up (↑) and down (↓) in energy, respectively. Their sum is the measured current I↑ + I↓ = IB,tot. ΔEB is the energy barrier change that is caused by the Zeeman shift at increasing magnetic fields, and it is, therefore, ΔEB = |ϕshift| for both spin bands. In our calculations, m* and d are the effective mass and thickness of hBN and h and q are the Planck constant and electric charge, respectively. The tunnelling voltage bias is denoted by VG. Since the energy barrier at B = 0 can be extracted from our data (Fig. 1d), the new energy barriers and the energy barrier change can be calculated14. From the argument presented above, we can match this energy change with the Zeeman splitting as ΔEB = g*µBB, and extract the total effective g-factor by fitting the magnetic field dependence of the energy barrier change (Fig. 2d). This allows us to obtain g-factors of holes of 1.22 ± 0.09 and 1.20 ± 0.12 for positive and negative fields, respectively. Since g* = ghBN – gInSe = 1.05, this value is in agreement with our calculated g-factor of the spin bands of hBN with a minor negative contribution of InSe (Fig. 2e,f). We note that this method is remarkably sensitive to changes in the energy barrier, with a minimum change detected on the order of ~15 μeV (Supplementary Note 5). To clearly detect such a signal, the measurement has to be performed at millikelvin temperatures to reduce the thermal noise.

Chirality-sensitive tunnelling differential conductance

The explanation provided above naturally raises the question of how the observed signal depends on the incoming light polarization, since the proposed mechanism relies on spin-polarized bands to either enhance or reduce the tunnelling process. InSe has indeed been shown to possess optical selection rules that enable coupling between chirality and spin, similar to valley physics in transition metal dichalcogenides9,35,36,37,38,39 (Supplementary Note 3). To investigate such a coupling, we excite with circularly polarized light (σ+ and σ–) and record the tunnelling current change as a function of the magnetic field. As shown in Fig. 3a, the tunnelling current shows an asymmetric behaviour. Specifically, the current increases for a positive (negative) magnetic field under σ– (σ+) light polarization. The signal recorded at a positive (negative) field under σ– (σ+) excitation matches well with the signal measured under linearly polarized light. This suggests that specific spin-polarized bands are available as the final states for carriers tunnelling from InSe. Moreover, changing the chirality of the incoming light and keeping the magnetic field fixed produced a detectable tunnelling differential conductance, which allowed us to electrically detect light chirality. We note that the system under study does not possess any intrinsic spin polarization40,41 nor chirally selective molecules42,43,44,45 or lattice structure5. To the best of our knowledge, this is the first material showing such a chirality-sensitive effect in the absence of a pre-existing state of broken time-reversal symmetry.

Fig. 3: Chirality-dependent tunnelling current response.
figure 3

a, Magnetic field dependence of the tunnelling current (ITC) measured at VG = −6 V and 250 μW of laser power for the 5L device. The signal is shown for different excitation chiralities (linearly polarized (LP), and left- and right-handed circularly polarized). The current observed at a positive (negative) magnetic field for σ– (σ+) is equivalent to the linearly polarized response. This allows us to electrically detect the chirality of light at a given magnetic field in an originally achiral system. The asymmetry is caused by the Zeeman splitting of the hBN bands, which now presents a different energy barrier height for different spin populations in the InSe layer, thereby favouring one population when the respective energy barrier is lowered. b, Tunnelling differential conductance (GTDC) can be extracted for different InSe layer numbers and multiple devices, showing that the observed signal is independent of the InSe layer number. Two examples are shown: 3L (blue) and 5L (red). Interestingly, the tunnelling differential conductance increases linearly with the magnetic field, and a total value of around 5% is obtained at ±5 T and 150 μW. The errors plotted are the standard deviations of the conductance values within the specified intervals.

Full size image

We can further quantify the tunnelling differential conductance for different thicknesses of InSe as a function of the magnetic field, and the results are shown in Fig. 3b. The recorded tunnelling differential conductance shows a trend that is independent of the InSe thickness, consistent with the g-factor quenching in InSe multilayers. Such a signal increases linearly for both magnetic field polarities and reaches a value of ~6% at a magnetic field of ±5 T and 150 μW. To clarify, since the VBM of 3L InSe does not shift on the application of a magnetic field (negligible gz; Fig. 2e), the excitation generates carriers that can populate any of the six energy-degenerate valleys across the 3L InSe Brillouin zone hosting negligible spin expectation values, Sz ≈ 0 (Supplementary Fig. 5c). This is in strong contrast to the monolayer case that exhibits three valleys displaying spin-up-favoured states and the other three valleys having spin-down-favoured states26. Moreover, although the optical selection rules for in-plane polarized light are present in 3L InSe (Supplementary Note 3 shows the group theory analysis), the optical spin injection of holes is not an efficient mechanism mainly because Sz is strongly suppressed owing to the absence of a mirror plane. Consequently, the scattered holes that directly accommodate at the VBM will inherit a state of Sz ≈ 0. However, the presence of a spin-selective favourable state in hBN, due to the Zeeman shift, leads to the emergence of a spin-polarized current in addition to the unpolarized component. This spin-polarized current is responsible for the observed tunnelling differential conductance under chiral excitation (Fig. 3b).

Tunable spin-polarized hole currents

To better understand the observed emergent phenomenon, we perform magnetic field measurements of the tunnelling currents with different incoming light polarization and different excitation powers. We can define the degree of polarization for positive and negative magnetic fields as \({\delta }_{{\rm{P}}}^{\pm }=({I}_{{\sigma }_{\mp }}-{I}_{{\sigma }_{\pm }})/({I}_{{\sigma }_{+}}+{I}_{{\sigma }_{-}})\), where \({I}_{{\sigma }_{\mp }}{(I}_{{\sigma }_{\pm }})\) represents the current recorded under circularly polarized excitation σ– (σ+) for positive magnetic fields and circularly polarized excitation σ+ (σ–) for negative fields. The resulting degree of polarization of the tunnelling current is shown in Fig. 4a for both field polarities. The limited magnitude of \({\delta }_{{\rm{P}}}^{\pm }\) is explained by the out-of-plane spin polarization quenching in multilayer InSe. Spin-polarized hole currents can be successfully generated and measured in this configuration, marking the first observation of spin-polarized hole transport in metal monochalcogenide materials.

Fig. 4: Observation of hole spin accumulation at the band edge.
figure 4

a, Degree of polarization (DOP) for positive and negative magnetic fields (±5 T), defined as \({\delta }_{{\rm{P}}}^{\pm }=({I}_{{\sigma }_{\mp }}-{I}_{{\sigma }_{\pm }})/({I}_{{\sigma }_{+}}+{I}_{{\sigma }_{-}})\), where \({I}_{{\sigma }_{\mp }}{(I}_{{\sigma }_{\pm }})\) represents the current recorded under circularly polarized excitation σ– (σ+) for positive magnetic fields and circularly polarized excitation σ+ (σ–) for negative fields. Two regimes can be identified, with a low-power regime characterized by a constant DOP and a high-power regime characterized by a linear increase in the DOP as the laser power is increased (on a logarithmic scale). A vertical dashed grey line shows the division between the two regimes. The mechanism responsible for the observation of this phenomenon was predicted almost a decade ago26, and demonstrated here. b, Spin-polarized hole accumulation mechanism for monolayer InSe as discussed in the literature26, and revised for clarity. A spin-up electron is excited from the lower valence band to the CB, and it decays by recombining with a hole in the upper valence band with the same spin. As a result, oppositely polarized holes will accumulate in the upper valence band on recombination. This effect causes an increase in spin accumulation, which follows the trend observed in this work. c, Spin-polarized hole accumulation mechanism in multilayer InSe (ML InSe). In this scenario, a positive out-of-plane magnetic field (Bz > 0) causes the spin-up band of hBN to shift upwards in energy, reducing the energy barrier height for the spin-up carriers tunnelling from InSe. Thus, a spin-polarized current contribution is added to the unpolarized part, leading to the differential tunnelling conductance discussed in Fig. 3b. The upper valence band hosts carriers with spins lying prevalently in plane (orange arrows), causing the out-of-plane spin polarization to be reduced in our experiments. Importantly, since the spin accumulation is along the out-of-plane direction, the points neighbouring the VBM are responsible for such a spin accumulation to occur. Owing to the suppressed Sz and low g-factor at those points, the spin accumulation is rather modest, reaching ~10% at ±5 T. However, the ability to detect such a small spin polarization represents a remarkable result that is allowed by our method. Moreover, the observed spin polarization values follow the trend described by the theory26, confirming the physical origin of the observed phenomenon.

Full size image

Interestingly, two regions with different trends can be identified. A low-power regime characterized by a roughly constant signal and a high-power regime in which the signal exhibits linear growth with respect to the laser excitation power when plotted on a logarithmic scale. The low-power regime can be understood in terms of the Zeeman splitting discussed above, where the polarization degree results from the efficient tunnelling of spin-polarized carriers due to energy barrier height considerations.

On the contrary, with an increase in the laser power, even though the energy barrier height remains constant at a given field, the spin polarization increases up to almost ±15%. Since the carriers excited at higher laser powers primarily influence the magnitude of the effect without changing the tunnelling mechanism in this material14, we can interpret this result as a phenomenon that generates out-of-plane spin-polarized carriers at the VBM with increasing excitation power. Since the lowest CB and highest VB are connected by a sizable \({\hat{\pi}}_{z}\) optical matrix element, linearly polarized luminescence can be emitted along the in-plane direction on the radiative relaxation of electrons to the upper valence band26. The spin-conserving nature of this direct interband transition allows the accumulation of holes with opposite spin polarization at the valence band edge (Fig. 4b). In Fig. 4c, we show the schematic involving multilayer InSe. In this scenario, the out-of-plane spin component at the VBM is suppressed, leading to a reduced value of spin polarization with respect to the monolayer case. Importantly, such an out-of-plane spin accumulation is allowed in the VBM neighbouring points and can contribute to the observed signal (Supplementary Note 3). On the application of a positive (negative) magnetic field, the spin-up (spin-down) band of hBN shifts upwards in energy, reducing the energy barrier height for the tunnelling process of holes at the VBM for a specific spin population. Such a spin polarization mechanism at the VBM of InSe at increasing laser powers was theoretically predicted almost a decade ago26. However, it has remained elusive until now, primarily because of the challenges in generating hole currents for spin transport measurements at the valence band edge in this class of materials. In our approach, the exponential nature of the tunnelling mechanism provides us with the means to attain a detectable signal.

Outlook

The coupling between the chirality of light and spin is one of the most intriguing phenomena currently investigated in the area of condensed-matter physics. The possibility of engineering material platforms that exhibit chirality-dependent effects holds great promise for applications in the area of bioengineering and light–matter interaction in optoelectronic devices. In this work, we have investigated the magnetic field dependence of the tunnelling currents arising at the Van Hove singularity in few-layer InSe and their dependence on laser power and the chirality of light. By leveraging the exponential nature of the tunnelling current signal with respect to the energy barrier change and the negligible g-factor at the VBM of InSe along the z direction, we observed an uncompensated Zeeman shift in the valence spin bands in hBN. This allows us to determine the g-factor of holes in both hBN and InSe.

When subjected to linearly polarized light excitation, the variation in tunnelling current with the applied magnetic field exhibits symmetry. By contrast, when circularly polarized light is used, a tunnelling differential conductance becomes apparent. This intriguing observation enables us to electrically detect the chirality of light in a system that was initially achiral, marking a significant departure from previous reports10,43,44. Finally, our study confirmed a long-standing theoretical prediction by demonstrating an increase in spin polarization at the valence band edge under high laser powers26.

Our approach, utilizing tunnelling currents in few-layer InSe, showcases exceptional sensitivity to the energy barrier change and establishes a robust foundation for the investigation of spin physics and emergent phenomena in metal monochalcogenides in the presence of a magnetic field. Our devices demonstrate high reproducibility and potential for manufacturing, clearing the path for future investigations into chirality-dependent phenomena within field-effect structures based on two-dimensional materials8. Our results are expected to motivate further scientific exploration, fostering a deeper understanding of chirality-dependent phenomena and light–matter interactions in flat-band systems. Moreover, these findings hold promise for various technological applications, enriching the landscape of strongly correlated phenomena, and emergent physics in van der Waals heterostructures.

Methods

Device fabrication

The materials used throughout this work were purchased from NGS (graphene) and HQ Graphene (InSe). The heterostructures were assembled by the traditional pick-up transfer technique as done in our previous works23, after the exfoliation of building blocks on SiO2 and polydimethylsiloxane. The entire fabrication process was performed inside an argon-filled glove box (inert) to avoid any material degradation. The electrodes are fabricated by electron-beam lithography and electron-beam metal evaporation (2 nm/100 nm Ti/Au). The hBN flakes are selected to be within 18 nm and 30 nm as the thickness range, and the exact thickness is measured by AFM. For the 3L and 5L devices, the hBN thicknesses are determined to be 18 nm and 25 nm, respectively.

Optical and electrical measurements

All the measurements shown in this work are carried out at 100 mK inside a dilution refrigerator (Oxford Instruments), which is equipped with a vector rotator magnet that allows us to perform magnetic field measurements. The system is designed with a custom-made window that allows us to perform optical measurements at the base temperature, together with the transport measurements and monitoring the vacuum level. The excitation is performed by focusing a continuous-wave laser on a spot of about 1 µm diameter on the sample. The wavelengths used vary depending on the sample since the bandgap changes sensibly for different thicknesses of InSe. In particular, the above bandgap excitations are used, with λ = 648 nm and 532 nm, for 5L and 3L InSe, respectively. The incident power was varied from 1 µW to 300 µW for power dependence measurements (Fig. 4). Transport measurements were carried out at 80 mK with a Keithley 2636 source meter.

First-principles calculations

We conduct an assessment of the electronic, spin and orbital characteristics of InSe and hBN utilizing density functional theory. Our analysis uses the all-electron full-potential linearized augmented plane-wave methodology within the WIEN2k code46. In this investigation, we apply the Perdew–Burke–Ernzerhof47 exchange–correlation functional and incorporate van der Waals corrections through the D3 scheme48. The wave-function expansion takes orbital quantum numbers up to 10 into consideration, with a plane-wave cut-off set at 8 times the smallest atomic radii. Spin–orbit coupling is fully relativistically considered for the core electrons, whereas the valence electrons are treated with a second variational procedure49, with the scalar-relativistic wave functions calculated within an energy window up to 5 Ry. Self-consistency is achieved with convergence criteria of 10–6e for charge and 10−6 Ry for energy. We utilize a two-dimensional Monkhorst–Pack k-grid with 15 × 15 (15 × 15 × 5) points for trilayer γ-InSe (hBN). In the case of a single InSe layer, we adopt the lattice parameters available from the Computational 2D Materials Database50, where the in-plane lattice constant is 4.074 Å, the layer thickness is 5.3673 Å and the In–In distance is 2.81425 Å. Interlayer distances for γ-InSe are determined through energy minimization, resulting in a van der Waals gap of 2.923 Å or 8.29 Å if measured from the middle of the monolayers, consistent with previously calculated values of 8 Å (ref. 13). A 20 Å vacuum region is included for the γ-InSe system to prevent slab interactions. For bulk hBN, we utilize the lattice parameters from the Materials Project database51, where the in-plane lattice parameter is 2.512 Å, and the unit cell in the out-of-plane direction measures 7.707 Å. The calculations for orbital angular momenta are based on the fully converged summation-over-bands approach52,53,54,55.