Main

Rates of ice-sheet melt and associated sea-level rise (SLR) have been accelerating in response to global warming5. For the coming centuries, the Intergovernmental Panel on Climate Change5 expects that these rates will further increase to values not observed since the early Holocene1 (11.7–8.2 thousand years ago (ka); all dates are in calibrated years bp). Accurate forecasting of future climate and sea level depends on a robust understanding of the Earth-system response to external forcings (for example, solar and orbital) and changes in atmospheric composition6. Although the available instrumental records provide detailed information about the functioning of our planet, Earth-system feedbacks on multi-centennial to millennial timescales cannot be evaluated using these short records. It is therefore necessary to obtain palaeorecords of sufficient detail, from periods like the early Holocene, that provide model benchmarks and climate storylines for present and near-future conditions.

During the early Holocene, temperatures increased rapidly7, resulting in large-scale melting of the remnant North American Ice Sheet Complex (NAISC, here Laurentide, Innuitian, Cordilleran and Greenland ice sheets combined) and sectors of the Antarctic Ice Sheet (AIS). Early Holocene temporal changes in ice-sheet volume, as well as the modes through which meltwater reached the ocean (steadily or through pulses of proglacial lake-drainage events), have been reconstructed using empirical data8,9, modelling results10,11 or combinations of both12,13. Nevertheless, key uncertainties remain in terms of the timing of deglaciation and changes in ice-sheet volume. Patterns and rates of reconstructed relative sea level (RSL) are an important proxy for ice-sheet volume change and can therefore be used to calibrate and validate both ice-volume reconstructions14 and glacial isostatic adjustment (GIA) models10,14,15. However, there are few geological constraints on early Holocene sea level, especially when compared with the middle and late Holocene, for which thousands of onshore collected sea-level index points (SLIPs) are available2.

SLIPs are derived from dated indicators (for example, submerged peat layers, coral reefs and archaeological remains) that formed in close relationship with sea level and delimit the past position of sea level in space and time16. They are rare for the early Holocene, because records formed during that time typically occur offshore and are deeply buried, which makes them harder to sample. The limited early Holocene SLIP datasets that do exist have relatively large vertical uncertainties owing to: (1) low spatial sampling density (for example, isolated submerged mangrove peats17); (2) reliance on corals15,18,19 with relatively large depth–habitat ranges (often yielding 2σ uncertainties ≥8 m (ref. 20)); or (3) being substantially impacted by local ice loads21 (for example, rebound history). Where higher density and accuracy is reached, SLIP datasets do not extend before 9.5 ka (ref. 22). To fully employ the potential of using rates of SLR during the early Holocene to constrain rates of ice-volume change, regional SLIP series with high data density are required.

The North Sea region has an extensive shelf where such records are within reach of relatively low-cost shallow-depth sampling devices, with the advantage that temperate-latitude drowned-coastal marsh SLIPs sampled there have the potential for decimetre-scale precision16, although the region experiences proximal solid-earth responses to ice-loading patterns of the nearby Eurasian Ice Sheet (EuIS)23,24,25. At the start of the Holocene, a large part of the North Sea was still dry land, over which widespread peat formation occurred before the archaeological ‘lost world’ of Doggerland3,4 was submerged in response to rising sea level. Despite subsequent erosion by coastal and marine processes, large stretches of these blanketing peats have been preserved25,26. All previous sea-level studies in the North Sea region relied on relatively few legacy data points25,27 that are spatially isolated and show considerable discrepancies within and between subareas. These legacy data also have vertical uncertainties up to 4 m (2σ), which poorly constrain the early Holocene North Sea RSL and limit their usefulness in evaluating regional and global GIA modelling. As a result, the regional GIA contribution to modern SLR remains uncertain28,29, complicating the translation of scenarios of future global SLR into regional predictions30,31. Poorly constrained rates and magnitudes of RSL also mean that the magnitude, rate and timing of the contribution of late-stage deglaciation of the NAISC and the AIS to the global mean sea level (GMSL) remain uncertain. This is problematic as future SLR will be fuelled again from the melt of both the NAISC (primarily the Greenland Ice Sheet component) and the AIS. Hence, a comprehensive understanding of the complex interactions between climate, sea level and ice sheets during a rapidly warming global climate is required.

To better constrain rates of both the GMSL and the North Sea regional RSL, we obtained early Holocene SLIPs from the North Sea during multiple research cruises (Fig. 1). We applied GIA modelling to quantify the spatially varying contribution of the EuIS to the RSL in the North Sea. We then subtracted this EuIS contribution from each SLIP to isolate the combined contribution of the NAISC and the AIS to the GMSL (see Extended Data Fig. 1 for our workflow).

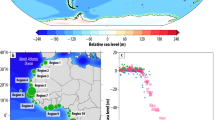
Fig. 1: Plot of all SLIPs and limiting data points.
figure 1

The inset shows the locations of the data and the used seismic lines. Upper limiting data points provide an upper bound on the past position of the RSL and lower limiting data points provide a lower bound. The plotted RSL data points are corrected for compaction, palaeotidal variability and non-GIA background basin subsidence, but retain a spatially variable GIA signal. Bathymetric data in the inset were downloaded from EMODnet (https://emodnet.ec.europa.eu/en/bathymetry). WGS1984 is the World Geodetic System.

Full size image

Sea-level data

The flooding of the North Sea is recorded in geological sequences that generally comprise a peat bed (0.1–0.3 m thick) overlying sandy Pleistocene deposits, and conformably underlying brackish marine muds25,32 (Fig. 2). Such transgressed-peat sequences formed extensively throughout the area during periods of early Holocene RSL rise, and the record of their drowning can be used to extract past sea-level positions. Erosion by subsequent shelf-sea dynamics led to a patchy preservation of in situ peat, typically buried by lags of shelly sands but locally by brackish muds. National borehole databases and geophysical data were used to target the collection of offshore vibrocores that contain the early Holocene peat–mud contact. We analysed diatom assemblages contained within the sediments and X-ray fluorescence (XRF) core-scan data to identify the palaeoenvironment recorded within the core and to assess whether the peat–mud contact is non-erosional.

Fig. 2: Example of a sampled sequence.
figure 2

The vibrocore reaches 3.8 m below the North Sea floor, with transgressed peat (basal peat) in photographed segment 1–2 m, and depth-aligned results for this segment representative of subsampling strategy and resolution of logging, dating, geochemical and palaeoenvironmental investigation to generate offshore sea-level data. Figure collated from materials in supplementary information sections 1 (14C dating) and 2 (core photos, stratigraphic description, XRF core-scan results, diatom results; detailed single and multivariate geochemistry and diatom-species counts found in there)49. BDEU0698NE = Core ID; SLIP, sea-level index point; ULD, upper limiting data point; cal, calibrated; Incoh./coh., Incoherent/coherent.

Full size image

Radiocarbon-dated samples from the bottom and mud-covered top of the peats constrain the age of the start and end of peat formation and provide details of the timing of transgression of the Holocene North Sea (Doggerland) landscape. We combined 88 sea-level data points with 51 legacy data points from the Dutch and German sectors of the North Sea. Legacy data from the British North Sea sector21 were not included, to avoid unwanted uncertainty caused by the regional British Ice Sheet load. The base of the peats yielded upper limiting data points (72 database entries; limiting data provide only upper or lower constraints on the elevation of past sea level), whereas the top of the peats yielded 59 SLIPs. Top-of-peat dates marking a boundary with freshwater lacustrine sediments, rather than brackish muds, are regarded as upper limiting data points (nine entries), and dates obtained from within brackish muds are regarded as lower limiting data points (eight entries). Vertical corrections were applied for compaction, palaeotidal conditions33 and non-GIA background basin subsidence, with propagation of associated uncertainties (Methods). We used Bayesian age modelling on clusters of radiocarbon dates to enforce stratigraphical order and RSL attribution32, thus reducing chronological uncertainties. The 59 North Sea SLIPs (of which 42 were recently gathered; Fig. 1) have a mean vertical uncertainty of ±0.42 m (2σ) and a mean age uncertainty of ±184 yr (2σ), both much smaller than in earlier studies15,25 that had uncertainties on the order of ±2 m (vertically) and ±500 yr (in time) for the early Holocene.

The SLIP dataset in this study shows that the North Sea RSL was around −50 m at 11 ka and rose to −15 m in the following 3 kyr. To improve our GIA modelling results and to extend our analysis into the Middle Holocene, we supplemented the offshore North Sea dataset with the nearby, mostly onshore, sea-level dataset32 for the Rotterdam area (50 SLIPS; Fig. 1).

Early Holocene SLR

The southern North Sea region shows large spatial variations in post-glacial RSL, reflecting a regional GIA pattern resulting from the deglaciation history of the proximal EuIS14,23,25 (Extended Data Figs. 6–8). To isolate the EuIS GIA component (including melt of its remaining ice sheet) contained in the Holocene RSL records from that driven by NAISC and AIS melt, we used two published EuIS reconstructions: ICE6G10 and BRITICE-CHRONO14, combined with a suite of one-dimensional (1D) and three-dimensional (3D) Earth models. From this suite, we selected eight models (seven 1D and one 3D; Extended Data Table 1) to calculate the EuIS RSL contribution for all SLIPs in Fig. 1. The 7 combinations with a 1D Earth model capture the RSL signal within a 95% confidence interval; the best-performing 3D model does not, but was included nonetheless to address any bias towards the assumption of a 1D rheology (Methods). The BRITICE-CHRONO-modelled EuIS contributions to RSL produced the lowest misfits when compared with the 109 SLIPs (Fig. 3; see Methods for details).

Fig. 3: Absolute misfit between the SLIP-derived and modelled EuIS RSL signals.
figure 3

a–c, The BRITICE-CHRONO14 (a) and ICE6G10 (b,c) reconstructions are here combined with the 1D Earth model that produces the smallest misfit (a,b) and the largest misfit (c) (Extended Data Table 1). For BRITICE-CHRONO, this is a lithosphere thickness of 96 km combined with upper- and lower-mantle viscosities of 0.3 × 1021 Pa s and 20 × 1021 Pa s, respectively. For ICE6G, a lithosphere thickness of 96 km combined with upper- and lower-mantle viscosities of 0.5 × 1021 Pa s and 3 × 1021 Pa s, respectively (very similar to the VM5a Earth model, labelled ICE6G-smallest; b) and a lithosphere thickness of 71 km combined with upper- and lower-mantle viscosities of 0.5 × 1021 Pa s and 5 × 1021 Pa s, respectively (labelled ICE6G-largest; c).

Full size image

The best-fitting patterns with location-specific rates of EuIS GIA were subtracted from the SLIP observed RSL to generate a EuIS GIA-corrected sea-level dataset for the North Sea, with the standard deviation of the eight EuIS GIA-modelled predictions propagated in the uncertainty quantification. Thermosteric contributions (that is, the expansion of the ocean volume owing to temperature and salinity changes) during this time frame fluctuated around zero34, whereas variations in the extent of mountain glaciers during the Holocene can be expected to result in decimetre-scale GMSL changes only35,36. This means that after the EuIS contribution is removed from the RSL value of each SLIP, the resulting sea-level signal predominantly reflects the regional expression of the combined contribution of the North American and Antarctic ice sheets to early Holocene SLR. We label this signal ‘residual relative sea-level change’. The residual dataset was then processed with the Error-in-variables Integrated Gaussian Process (EIV-IGP) model37,38 that uses Bayesian inference to produce a continuous model (80-yr interval) of the rate of North Sea residual sea-level change (Fig. 4a). The high data density allows quantification of rates between 11 ka and 3 ka with a median uncertainty of ±1.4 mm yr−1 (2σ).

Fig. 4: Rates and magnitude of early Holocene SLR.
figure 4

a, Rates of North Sea residual RSL change for 11–3 ka (data in49), in relation to rates of GMSL change during the past 2 kyr (ref. 50) and expected for the next century5. b, North Sea residual RSL for 11–3 ka and the derived GMSL curve (dashed grey line) after accounting for regional NAISC–AIS sea-level fingerprint (this study). Also shown is GMSL during the past 2 kyr (ref. 51) and expected for the next century5. The inset axis shows our reconstructed8,12,46,47,48 GMSL contributions in metres SLE from three main ice-mass centres (NAISC, AIS and EuIS) with their mean value and 2σ range. Data from 2 to 0 ka reproduced from: a, ref. 50, under a Creative Commons licence CC BY 4.0; b, ref. 51, under a Creative Commons licence CC BY 4.0.

Full size image

Phases of accelerated SLR

Our reconstruction of residual RSL for the North Sea shows two phases of accelerated SLR that span several centuries (Fig. 4a), which are attributed to phases of enhanced NAISC and AIS meltwater release. The first phase (P1) peaks around 10.3 ka, with a rate of nearly 9 mm yr−1, matching the maximum projected rates of GMSL rise for 2150 ce (Fig. 4a). Towards 9 ka, the rates drop to 5.7 mm yr−1. The second phase (P2) peaks at 8.1 mm yr−1 around 8.3 ka. Thereafter, rates decline rapidly to around 1 mm yr−1 by 7.0 ka and to 0 mm yr−1 by 5 ka. The negative rates between 5 ka and 3 ka are in line with evidence for regrowth of Antarctica during that time12,34. The total North Sea residual sea-level change between 11 ka and 3 ka was 26.3 m (2σ range, 23.8–28.8 m; Fig. 4b).

In line with the timing of P2, several studies have identified the final, most likely two-staged drainage event39 of Lake Agassiz–Ojibway, and related disintegration of sections of the NAISC, to be an important contributor to an accelerated phase of GMSL rise between 8.5 ka and 8.2 ka (refs. 32,40). This meltwater-release event explains a considerable part of P2 as Lake Agassiz–Ojibway alone contained an estimated 0.45 m sea-level equivalent (SLE)41. The remaining part of the SLR came from background melt of remnants of the Last Glacial ice sheets (with similar rates of SLR as at 9 ka)32. Without the storage of large quantities of meltwater in Lake Agassiz–Ojibway, the reconstructed dip in rates of SLR around 9 ka would have been smaller, and the peak in rates of SLR during P2 lower. It must be noted that during the drainage events, global rates of SLR were higher than 10 mm yr−1 for relatively short periods of time32,40.

By comparison, the timing, duration and magnitude of the rate of SLR during P1 has not been explained by any documented regionally sourced lake-drainage event. Recent work from the Labrador Sea, however, reports increased meltwater discharge between 10.64 ka and 10.15 ka (ref. 42), followed by a prolonged period of considerably lower meltwater discharge that increased again after 8.74 ka.

The large-scale meltwater-release signal observed between 11 ka and 8 ka from along the southern and eastern limits of NAISC42 thus aligns with the pattern found in the continuous, high-resolution record of the early Holocene residual RSL for the North Sea, with its vertical and temporal changes over multiple millennia. Herein, we consider P1 to be mainly a peak in ice-derived meltwater, directly linked to rapid climatic warming during the early Holocene. Several temperature records indicate that around 10 ka, global temperatures started to stabilize7, perhaps reflected in the timing of P1 termination. The warming would have set on at 11.7 ka (ref. 7), currently just out of reach of the North Sea SLIP data series. The rising limb of P1 as currently resolved (11–10.3 ka) consequently suffers from relatively large uncertainty that can be reduced only by obtaining additional SLIPs, for example, by sampling deeper lying and older peats from the North Sea. In contrast to P1, P2 has a more complex nature. It reflects a combination of the steady melt of ice sheets with the rapid release of water temporarily stored in large proglacial lakes and the associated rapid disintegration of parts of the Laurentide Ice Sheet.

GMSL and ice-sheet contributions

The North Sea residual RSL rise is the regional expression of early Holocene GMSL rise owing to steady loss of global land ice (Fig. 4b). The position of the North Sea with respect to the gravitational fingerprints of the Late Glacial and early Holocene ice sheets means that its early Holocene residual sea-level record captures 74% (2σ range, 68–90%) of GMSL (Methods and Extended Data Fig. 11). The 26.3 m (2σ range, 23.8–28.8 m; 74%; Fig. 4b) rise of North Sea residual RSL between 11 ka and 3 ka therefore translates to a global NAISC–AIS SLE of 35.5 m (2σ range, 27.1–40.0 m; 100%). Adding the EuIS contribution of 2.2 m SLE (2σ range, 1.5–2.9 m; see below) after 11 ka results in a total GMSL rise between 11 ka and 3 ka of 37.7 m (2σ range, 29.3–42.2 m). Far-field sea-level curves for the same period indicate a larger GMSL rise of 45 m to 55 m (refs. 15,19; with uncertainties estimated at ±5–10 m). This substantial mismatch is to be attributed in part to not accounting for spatially varying GIA-fingerprinting effects across widely scattered far-field shelf and island locations that can vary between 80% (ref. 43; for example, Barbados coral site) and 120% (ref. 43; for example, Tahiti coral site), and also to differing rates and modes of non-GIA subsidence/uplift between sites, and the complexities and associated large uncertainties when using coral as a sea-level indicator20.

To evaluate the relative contribution of melt from the AIS, NAISC and EuIS to Holocene GMSL, we utilize published deglacial models and ice-sheet reconstructions. Constrained by geological data12, recent deglacial simulations suggest that the AIS contributed 7.8 m SLE over the 11–3 ka period (2σ range, 4.1–9.6 m), in line with an earlier estimate44. By contrast, another recent study estimated the AIS-derived contribution to GMSL over the same period as closer to 4 m SLE45. Using geologically mapped ice-sheet extents8, our volumetric reconstructions of the NAISC over its deglaciation suggest that this ice-sheet complex contributed 29.7 m SLE (2σ range, 23.4–36.0 m) between 11 ka and 3 ka. The meltwater contribution of the EuIS over this period is much smaller, as its deglaciation was already nearly completed by the time the Holocene began: only 2.2 m SLE (2σ range, 1.5–2.9 m) after 11 ka (refs. 46,47,48).

Summing these respective ice-sheet contributions for 11–3 ka (Fig. 4b) results in a total GMSL rise of 39.7 m (2σ range, 32.3–46.3 m), in good agreement with the 37.7 m (2σ range, 29.3–42.2 m) of GMSL rise we calculate based on the North Sea SLIPs. This reconciles the mismatch that existed between GMSL estimates based on ice-sheet reconstructions and previously limited and location-specific early Holocene sea-level data15,19.

Our residual RSL record for the North Sea, which covers an area of approximately 80,000 km2, highlights the importance of collecting densely sampled offshore RSL data with extensive overall spatial coverage. Such an approach offers improved constraints on ice-sheet reconstruction and GIA modelling for critical periods when ice sheets last melted as rapidly as anticipated in future GMSL projections. Specifically, it helps to constrain estimates of background GIA in both current regional RSL and projections of future SLR. Hence, we recommend (1) further early Holocene SLIP collection with similar spatial coverage and density as in the North Sea at selected shelf-sea sites worldwide, and (2) extension of data collection to the Late Glacial period, with North Sea seismic data showing accessible peat records to depths of about 80 m. Importantly, early Holocene sea-level data have an additional, direct application in geological, palaeoenvironmental and archaeological reconstructions of drowned shelf landscapes worldwide. By understanding the rapid RSL-driven flooding of these once-fertile lowlands and important land bridges, these data records can shed light on one key driver of human migration in places such as Doggerland in northwest Europe3,4. Dealing with climate change and rapid SLR is not unique to modern society.

Methods

Before detailing each step in our methodology in the following sections, we first explain the main rationale behind our approach to distil a GMSL curve from our North Sea sea-level dataset for the 11–3 ka period. The dataset is used to construct SLIPs (steps 1 and 2 in Extended Data Fig. 1) that show strong spatial variation in RSL histories owing to the proximal location of the North Sea region to the EuIS and the resulting non-uniform EuIS GIA signal. This signal consists mostly of a vertical-land-motion component, because EuIS volume loss constitutes only 2.2 m SLE (2σ range, 1.5–2.9 m) after 11 ka (refs. 46,47,48). To isolate the much larger Holocene ice-sheet volume loss from the NAISC and the AIS, we subtracted the predicted EuIS GIA signal from the observed SLIP value. The resulting sea-level signal is labelled ‘residual relative sea-level change’.

The predicted EuIS GIA signal was calculated by running a large array of GIA models (both 1D and 3D) and selecting the best-performing models (seven 1D models and one 3D model; step 3). For performance testing of the GIA models, we included the existing, adjacent Rotterdam sea-level dataset that was gathered mostly onshore and has the same high level of spatial and temporal resolution32. The residual RSL record (step 4) is of smaller vertical range and spatially much more uniform than the RSL record produced in step 2. The residual RSL record therefore is considered a regional expression of the contribution of meltwater coming from the NAISC and the AIS to early Holocene SLR. We prefer this approach of obtaining a residual RSL record over simply using the eight selected GIA models directly to calculate the NAISC and AIS contributions in the early Holocene, as this would neglect the independent and observational value of the geological sea-level data and mainly mimic the NAISC and AIS reconstructions that were used in the GIA model itself.

In step 5, we used the residual sea-level data to construct a North Sea residual RSL curve for 11–3 ka and calculate rates of SLR with the Bayesian EIV-IPG model37,38. In step 6, we determined a sea-level fingerprint correction factor specific to the region and early Holocene time frame and used it to convert the North Sea residual RSL curve to a GMSL curve for 11–3 ka.

Our sea-level data (steps 1 and 2)

National borehole databases52,53 guided the identification of offshore locations with good prospects of preserved peat sequences within maximum target depths reachable by vibrocoring. During research cruises in 200954, 201155, 201756 and 2018, geophysical surveys were undertaken using sub-bottom profilers, boomers and sparkers to map the distribution and depth of the peat along 4,400-line km, used to determine exact core locations. Up to 6-m-long vibrocores were then retrieved, cut in metre-long sections, stored at 4 °C, transported to land, split lengthwise, and sedimentologically and stratigraphically logged (for all cruises). Vibrocores for the 2017–2018 cruises were also XRF-scanned (Extended Data Fig. 1, step 1).

Tops and bases of compacted peat beds resting on consolidated substrates were subsampled for the identification and selection of macrofossils for accelerator mass spectrometry radiocarbon dating (Fig. 2; see also supplementary information section 1 (supplementary information is available on Zenodo at https://doi.org/10.5281/zenodo.10801302 (ref. 49)). From several cores, diatom assemblages were identified (Fig. 2). The combined information was used to produce a database of RSL data points (Fig. 1) following the HOLSEA protocol2,32 (Extended Data Fig. 1, step 2). Additional data fields were included to specify (1) a series of vertical correction terms (decompaction, palaeotidal variability, background basin subsidence), (2) the Bayesian radiocarbon age calibration57, and (3) the labelling as SLIP, upper limiting (sometimes called terrestrial in literature) or lower limiting data point, or rejected point. Legacy data were also entered into the database and were re-analysed with the same protocol. Supplementary information section 1 contains the full database, including technical documentation for contents and calculation of each field and supplementary information section 2 contains the analyses of the XRF and diatom data, as well as core photos49.

Extended Data Fig. 2 presents a sensitivity analysis (Extended Data Fig. 1, step 5) of the impact of each correction term on the calculated rates of MSL rise. It shows a relative insensitivity to the applied compaction correction (decompaction factor of 3 ± 0.5 based on modelled bulk density58), because the majority of the SLIP-providing peat beds were <0.3 m thick. Rates are more sensitive to the incorporation of palaeotidal information33,59,60,61 (literature-obtained amplitudes ±37.5% uncertainty32; supplementary information49 section 1) when converting from mean high water (the reference water level for SLIPs from drowned peats in this area62,63) to MSL. The correction for background basin subsidence (that is, non-GIA vertical land motion) is most impactful, albeit spatially variable, with maximum upwards corrections of 2.7–2.9 m for 11-ka-old SLIPs from the subsidence centre (Extended Data Fig. 3). In our specification of background basin subsidence across the study area, we made use of a recently compiled data product considering the geologically mapped thickness of North Sea Basin fill for two periods: postdating 2.6 million years ago (Ma; regionally mapped; ‘base Quaternary’) versus postdating 1.8 Ma (subregionally known; ‘base Olduvai’) (supplementary information49 section 3; combining onshore and offshore data products of Dutch and German geological surveys; also used in the analysis of a recent Last Interglacial sea-level database64).

Bulk sediment (2009–2011 cruises) or selected macrofossils (2017–2018 cruises) from thin (mostly 0.02 m thick) slices of the top and bottom of the peat were submitted for accelerator mass spectrometry 14C dating. Bayesian age calibration (executed in OxCal 4.457 with IntCal2065; making use of the vertically ordinal Sequence-formulation of its Chronological Query Language) was set up for subregional data clusters (supplementary information49 section 1). The rationale for doing so32 is that the density of sampling allows the sorting of spatial selections of data points based on RSL age–depth position, exploiting the continuous RSL rise tendencies16,66 of basal peats. Applying a priori stratigraphic ordering reduced the 2σ age range of the legacy data (52 dates from samples collected before 2010) from 766 years to 459 years (40% reduction), and the 2σ age range of the post-2010 data (N = 87) from 422 years to 327 years (22% reduction). Extended Data Fig. 2 shows that including Bayesian age calibration had a small impact on P2, but for P1 peak rates increased almost 1 mm yr−1 and the midpoint shifted by a century.

Selecting GIA models (step 3)

To investigate which drivers contribute to the RSL signal across the southern North Sea, we used both 1D and 3D global GIA models to produce RSL predictions. All models (1) require an input ice-sheet reconstruction, which defines the spatial and temporal history of major grounded ice sheets during the last glacial period, and (2) solve the generalized sea-level equation by including time-dependent shoreline migration as well as sea-level change in regions of ablating marine-based ice67. Only the 1D GIA models include the influence of rotation of Earth on the sea-level calculation68,69. However, comparison of the results from the 1D GIA model with and without rotation showed negligible differences across the study period. The main difference between the 1D and 3D models is in the approach used for the calculation of the deformation of Earth (that is, the Earth model). In the 3D GIA model, the viscosity varies both laterally and with depth, whereas in the 1D GIA model, viscosity varies only with depth.

We used ICE6G_5C10 (labelled as ICE6G) as the background input ice-sheet reconstruction to define the history for the NAISC and the AIS. This background reconstruction was combined with two reconstructions for the EuIS (consisting of the Scandinavian, Barents–Kara Sea, British–Irish and North Sea ice sheets): (1) ICE6G and (2) BRITICE-CHRONO14,70. The ICE6G EuIS model was developed iteratively using a 1D GIA model to capture the signal in the δ18O curve and far-field sea-level data10. The BRITICE-CHRONO EuIS model was developed independently of GIA modelling. Using a plastic ice-sheet model71, the spatial and temporal history of the ice sheet was constrained to fit geomorphological and geochronological information (see ref. 14).

The 1D GIA model adopts a spherically symmetrical Maxwell viscoelastic Earth model with three user-defined parameters: lithosphere thickness (km) and upper- and lower-mantle viscosity (Pa s). To investigate the optimum set of 1D Earth model parameters for each input EuIS reconstruction, we used 1D Earth models with two lithosphere thickness values (71 km and 96 km) combined with upper- and lower-mantle viscosities in the range of 0.1 × 1021 Pa s to 1 × 1021 Pa s and 1 × 1021 Pa s to 50 × 1021 Pa s, respectively, which amounted to 108 models (Extended Data Table 1). As the model was run at a 0.5-ka temporal resolution from 122 ka to 0 ka, linear interpolation was used to produce predictions at the weighted mean age of each SLIP.

For the 3D GIA model, we used a finite-element model based on the method of ref. 72 with locally enhanced spatial resolution73. The high-resolution zone is centred on the Southern North Sea and has spatial resolution of around 25 km. The resolution outside this zone is increasing from 50 km to 200 km. Present-day topography was obtained from ETOPO2v274. We investigated several 3D viscosity models, constructed with two approaches. The first approach converts seismic velocity anomalies (SMEAN2) to viscosity anomalies75,76, using partial derivatives of seismic velocity to temperature that include anharmonic and anelastic effects77. The conversion assumes that velocity anomalies are caused by thermal anomalies, although compositional anomalies could also have a role. Therefore, we vary a scale factor between 0 and 1 in steps of 0.25 to account for different contributions of mantle composition or temperature77. The viscosity anomalies were added to the VM5a background viscosity profile10. The second approach uses an olivine flow law78 for diffusion and dislocation creep to directly compute strain. With this approach, temporally variable viscosity can be incorporated, which is relevant because the effective viscosity becomes dependent on stress during dislocation creep. This is akin to, but not the same as, transient rheology, which has been investigated in other studies79,80. The temperature of the upper 400 km is taken from the global lithosphere and upper-mantle WINTERC-G81 which relies on seismic data, gravity data and thermobarometric data to invert for temperature. The grain size and water content in the flow laws were varied over a range (1 mm to 10 mm, and 0 ppm, 500 ppm and 1,000 ppm)82. In total, 31 3D GIA model runs were created.

To evaluate which of the 1D and 3D viscosity profiles, when combined with the two input EuIS ice-sheet reconstructions (ICE6G and BRITICE-CHRONO), was most suitable for the study region, we calculated the chi-square misfit (Extended Data Table 1) for the range of Earth models and the 109 SLIP RSL observations using:

$${\chi }^{2}=\frac{1}{n}\mathop{\sum }\limits_{i=1}^{n}\sqrt{{\left(\frac{{o}_{i}-{m}_{i}}{{{\sigma }}_{i}}\right)}^{2}}$$
(1)

Here, oi and mi are the observed and predicted RSL, n is the total number of data points and σi is the 1σ RSL error. We have ignored time errors as they are small and uniform and will not lead to different selection of best-fit models. Applying a 95% confidence limit (calculated from an F-test) to identify a misfit region within which the best-fit models are found (red contours in EDF4) delimits a parameter space of only seven possible 1D upper- and lower-mantle viscosities. The selection of models is small as the SLIP data are sensitive to the choice of upper-mantle viscosity, a result that has been found for other regional RSL datasets as well14. The lowest misfits are associated with BRITICE-CHRONO ice-sheet reconstruction, with optimum parameters being a lithosphere thickness of 96 km, an upper-mantle viscosity of 0.3 × 1021 Pa s and a lower-mantle viscosity between 20 × 1021 Pa s and 50 × 1021 Pa s. The ICE6G reconstruction prefers a weaker lower-mantle viscosity, with values between 2 × 1021 Pa s and 5 × 1021 Pa s combined with an upper-mantle viscosity of 0.5 × 1021 Pa s, which is not surprising as this is close to the VM5a Earth model that was used in the creation of ICE6G10.

For several reasons, the misfit of the 31 3D viscosity models was notably larger than for the 1D models. One reason is related to the input seismic data that constrain the spatial pattern of the 3D viscosity model. Any errors in this dataset and in the conversion approach applied to it will directly translate into a worse misfit, which is only partially compensated by varying the scale factors or material parameters. Second, the ICE6G ice reconstruction is developed with the 1D Earth model VM5a, which means that 3D models probably have a worse fit than VM5a. Despite the larger misfit, we decided to also include the best-performing 3D GIA model in subsequent analyses, in an attempt to address any bias towards the assumption of a 1D rheology, as it is known from seismic models83,84 that lateral variations in Earth structure probably exist in and around Scandinavia, the North Sea and the British Isles.

The model runs that included stress-dependent rheology, which reduces viscosity when ice loading is applied, did not perform well. Therefore, we conclude that transient viscosity with a lower short-term viscosity would probably also not be preferred by the data. The 3D viscosity (Extended Data Fig. 5) and ice-sheet reconstruction with the lowest misfit come from ICE6G combined with the 3D Earth model SM9925 (SMEAN2 in combination with a scale factor of 0.25). In this profile, the viscosity decreases from Scandinavia to the west, reflecting the transition from the Scandinavian craton to the hotspot environment of Iceland. Viscosity also decreases southwards into the North Sea region. The lithosphere is not explicitly defined but follows from the effective viscosity; the larger viscosities beneath Scandinavia correspond to larger effective lithosphere thickness there.

In a next step, the eight selected distinct GIA models were selected to calculate the contribution of the EuIS to the SLIP observed RSL at the location of each data point and to calculate the residual sea-level signal (supplementary information49 section 4): five Earth models (four 1D and one 3D) combined with the ICE6G ice-sheet reconstruction and three 1D models combined with BRITICE-CHRONO ice-sheet reconstruction.

Isolating the EuIS signal (step 4)

The GIA-modelled RSL signal consists of major contributions from the EuIS and the NAISC, and a relatively small contribution from the AIS (Extended Data Fig. 6). Breaking down the individual contributions as a percentage of the total signal (Extended Data Figs. 7d–k and 8), it is apparent that the spatial variation in the observed GIA signal is primarily controlled by the forebulge generated by the EuIS, with the two input ice-sheet reconstructions (ICE6G and BRITICE-CHRONO) producing different orientations and positions (Extended Data Fig. 6b,c). The EuIS is by far the largest contributor to the total RSL, with more than 50% at all sites (Extended Data Figs. 7 and 8). In contrast, the AIS contributes between 0.2% and 16%, lowest for sites near the present-day coastline. Although the NAISC is predicted to contribute up to 45% for the older sites in the central North Sea, it is always smaller than the EuIS contribution. Its spatial variation across the offshore SLIP-covered region, mainly caused by gravitational and water loading effects, at any time is small (Extended Data Fig. 8).

We define that the predicted sea level (total predictedrsl) at any given latitude (θ), longitude (φ) and time (t) can be separated into the predicted (p) contributions from the major ice sheets:

$${{\rm{Total\; predicted}}}_{{\rm{rsl}}}(\theta ,\varphi ,t)={{\rm{pNAISC}}}_{{\rm{rsl}}}(\theta ,\varphi ,t)+{{\rm{pAIS}}}_{{\rm{rs}}}(\theta ,\varphi ,t)+{{\rm{pEuIS}}}_{{\rm{rsl}}}(\theta ,\varphi ,t)$$
(2)

Using equation (2), we calculated both the observed (obsEuISrsl) and predicted (pEuISrsl) EuIS signal by subtracting the predicted contribution from the NAISC (pNAISCrsl) (Extended Data Fig. 7e,g) and the AIS (pAISrsl) (Extended Data Fig. 7d,f) from both the observed (Extended Data Fig. 7a) and predicted total RSL (Extended Data Fig. 7b,c):

$${{\rm{obsEuIS}}}_{{\rm{rsl}}}(\theta ,\varphi ,t)={{\rm{obs}}}_{{\rm{rsl}}}(\theta ,\varphi ,t)-{{\rm{pNAISC}}}_{{\rm{rsl}}}(\theta ,\varphi ,t)-{{\rm{pAIS}}}_{{\rm{rsl}}}(\theta ,\varphi ,t)$$
(3)
$${{\rm{pEuIS}}}_{{\rm{rsl}}}(\theta ,\varphi ,t)={{\rm{total\; predicted}}}_{{\rm{rsl}}}(\theta ,\varphi ,t)-{{\rm{pNAISC}}}_{{\rm{rsl}}}(\theta ,\varphi ,t)-{{\rm{pAIS}}}_{{\rm{rsl}}}(\theta ,\varphi ,t)$$
(4)

For equations (3) and (4), we used the predicted RSL from the eight models mentioned above (Extended Data Fig. 7d–g and Extended Data Table 1). We calculated the absolute misfit (in metres) between the predicted and observed EuIS to assess how well the EuIS signal is captured across our study region (Fig. 3).

Residual RSL change (step 5)

To calculate residual RSL change for the North Sea region, we first isolated the combined NAISC and AIS contribution to the RSL at each SLIP location using

$${\rm{o}}{\rm{b}}{\rm{s}}{\rm{N}}{\rm{A}}{\rm{I}}{\rm{S}}{\rm{C}}+{{\rm{A}}{\rm{I}}{\rm{S}}}_{{\rm{r}}{\rm{s}}{\rm{l}}}(\theta ,\varphi ,t)={{\rm{o}}{\rm{b}}{\rm{s}}}_{{\rm{r}}{\rm{s}}{\rm{l}}}(\theta ,\varphi ,t)-{\rm{a}}{\rm{v}}{\rm{e}}{\rm{r}}{\rm{a}}{\rm{g}}{\rm{e}}[{{\rm{p}}{\rm{E}}{\rm{u}}{\rm{I}}{\rm{S}}}_{{\rm{r}}{\rm{s}}{\rm{l}}}(\theta ,\varphi ,t)]$$
(5)

The uncertainty in obsrsl is taken from the HOLSEA database, whereas for average[pEuIS], the standard deviation calculated from the eight GIA models is used as a measure of uncertainty. From the resulting data series (supplementary information49 section 4), we calculated residual RSL and rates of residual RSL change with the EIV-IGP model37,38 (Extended Data Fig. 9), showing 26.3 m (2σ range, 23.8–28.8 m) of residual SLR for the 11–3 ka period (Fig. 4a).

Ice-sheet contributions (step 6)

Volumes of ice melt produced by ice sheets can be expressed in metres SLE, which is the average rise of global sea level if the volume is spread evenly across the world ocean surface. Step 6 considered the SLE contributions of the EuIS, NAISC and AIS, for both the period 11–3 ka and the entire Holocene (11.7–0 ka), reviewed from published data, independent of global GIA or sea-level modelling. To convert melted ice volume (km3) to metres SLE we used the average (2.51 m per 106 km3) of published values85.

At its maximum extent during the last glacial, the EuIS consisted of three main sectors46: the British–Irish Ice Sheet, the Fennoscandian or Scandinavian Ice Sheet, and the Svalbard–Barents–Kara Ice Sheet. At the start of the Holocene, however, the British–Irish Ice Sheet and the Svalbard–Barents–Kara Ice Sheet were almost gone. The Fennoscandian Ice Sheet contributed meltwater to the GMSL rise until about 10 ka (refs. 46,47,48). Three studies46,47,48 indicate that the EuIS-derived SLE was 2.2 m (2σ range, 1.5–2.9 m) between 11 ka and 10 ka and 3.0 m (2σ range, 2.1–4.3 m) between 11.7 ka and 10 ka (supplementary information49 section 4).

Contributions from the NAISC were calculated using a recently published reconstruction of its extent through the Holocene8. Mapped NAISC areal extents (A in km2) at specific time slices from this Holocene reconstruction were converted to ice volume (V in km3) using a relationship for dome-shaped ice-sheet sectors86: logV = 1.25(logA − 1.13). This relationship has been used for parts of the NAISC87, but not yet for all its sectors. The ice-volume uncertainty was calculated using published estimates of uncertainty in ice-sheet extent per time8. As an example, for 11 ka this means that the minimum ice-sheet volume equals the reconstructed ice-sheet volume for 10.3 ka and the maximum ice-sheet volume equals the volume of 11.8 ka (Table 1 in ref. 8).

The published volume–area relationship86, however, was developed for a single ice sheet with one dome in the centre, whereas the NAISC initially consisted of interconnected ice sheets with multiple domes (that is, Greenland and Innuitian ice sheets; Foxe-Baffin, Labrador and Keewatin domes of the Laurentide Ice Sheet). Only after the events that led to P2 did these respective sectors became fully disconnected8,88. Applying the volume–area relationship of ref. 86 in a situation of interconnected ice sheets would lead to an overestimate of the volume in ice, as this would imply one very high dome in the centre of the interconnected area. An alternative approach would be to first split the interconnected ice sheets into subareas surrounding the individual domes and use the area–volume relationship. This leads, however, to an underestimation of the total volume in ice, as this would imply zero thickness at the edges of the ice sheets, whereas in reality, saddles with considerable thickness were present. As a compromise, we used both approaches for the time frames with interconnection (everything before 8.5 ka) and then averaged the resulting changes in ice volumes as an approximation of the contribution of the NAISC to the GMSL. Summing this to an ice-volume history suggests that the NAISC contained 40.8 m SLE (2σ range, 31.6–50.0 m) at 11.7 m SLE and 36.5 m SLE (2σ range, 30.2–42.8 m) at 11 ka. By 3 ka, the remaining NAISC ice volume was 6.8 m SLE (mostly Greenland Ice Sheet; 2σ range, 6.8–6.9 m), which makes for a NAISC contribution of 29.7 m SLE (2σ range, 23.4–35.6 m) between 11 ka and 3 ka, and 34.0 m SLE (2σ range, 24.8–43.2 m) over the entire Holocene (supplementary information49 section 4). As a validity check, we compared our results with a recent global ice-sheet reconstruction (PaleoMIST1.0)89 that gives ice-volume changes per 2.5 kyr (about 10 times coarser than our main results based on North Sea observations and about 5 times coarser than the NAISC reconstruction above based on volume–area relations). For the NAISC, the PaleoMIST reconstruction89 shows a linear decrease in loss of volume between 17.5 ka and 5 ka that suggests that 33.3 m SLE has been lost since 11.7 ka, and 28.1 m after 11 ka, in agreement with our review and calculation.

To calculate the contribution of the AIS to GMSL, we used recent ensembles of deglacial simulations that are constrained by geological observations12. We used the ten top-scoring simulations highlighted in that paper to calculate a median contribution from the AIS of 7.8 m SLE between 11 ka and 3 ka (2σ range, 4.1–9.6 m SLE; supplementary information49 section 4). For the duration of the entire Holocene, our calculations show 8.1 m SLE (2σ range, 5.2–9.8 m SLE). All of these simulations indicate that the AIS was smaller than present at some point during the Holocene.

For the period 11–3 ka, the combined EuIS–NAISC–AIS contribution is then 39.7 m (2σ range, 32.3–46.3 m). For the entire Holocene, it is 45.1 m (2σ range 35.4–54.6 m).

Global mean SLR (step 6)

In the North Sea (midpoint of our offshore data), residual RSL rise amounts 26.3 m (2σ range, 23.8–28.8) between 11 ka and 3 ka because of ice melt on the NAISC and the AIS. Globally, this value would be different from region to region, as a consequence of GIA effects, including gravitation90. The spatial pattern in SLR across the world ocean and its marginal seas, which is generated as an output of global GIA modelling, is known as the fingerprint. It can in turn be broken down into component fingerprints for mass changes of respective ice-sheet complexes, be it the NAISC and the AIS in the early Holocene, or the Greenland Ice Sheet and the AIS in the modern situation. For a given increase of global-ocean volume in metres SLE coming from single or multiple mass sources, the fingerprint can be expressed as a percentage of GMSL rise (less than 100% of GMSL rise in the near to intermediate field; more than 100% in the far field). Relative fingerprint maps have also been used inversely, for instance, to identify the source of meltwater pulses43 and to convert locally reconstructed magnitudes of sea-level jumps (metres RSL change), to equivalent globally averaged magnitudes (metres SLE40,91,92).

We applied such inversion to assess GMSL between 11 ka and 3 ka. During this time, the source of GMSL rise was the NAISC for about three-quarters of the total GMSL (Fig. 4). As the composite fingerprint of the NAISC, the AIS and other potential sources is a mass-weighted one, the NAISC fingerprint will be dominant in the North Sea region. This also goes for sensitivity to mass changes and shifts of the NAISC mass centre during early Holocene deglaciation, as the NAISC is more proximal to the North Sea than the AIS. The dominance can be expected to disappear at some point within the middle Holocene (8.2–4.2 ka, probably after 7 ka) when NAISC deglaciation was completed, with the Greenland ice mass surviving and stabilizing8,88. A direct comparison of GMSL curves from ICE6G10 and PaleoMIST89 with both the observed (geological data) and predicted RSL (GIA modelling with all ice sheets) for our SLIP locations shows the GMSL to lie well above North Sea RSL, especially in the early Holocene (Extended Data Fig. 10a–d), reflecting the strong GIA signal from the nearby EuIS. Extended Data Fig. 10 also shows that the predicted RSL (Extended Data Fig. 10c,d) has much greater scatter than the observed RSL (Extended Data Fig. 10a,b), highlighting the uncertainty within the GIA modelling output when predicting RSL for areas near former ice sheets. After removal of the EuIS signal in the RSL data, both GMSL curves now plot below the North Sea residual RSL data as a result of the combined NAISC–AIS fingerprint (Extended Data Fig. 10e,f).

To assess this fingerprint for the 11–8 ka period, the model predictions for each SLIP location (excluding the EuIS signal) were divided by the GMSL value for the time the SLIP was formed. This shows that the North Sea region captured 74% (2σ range, 68–90%; Extended Data Fig. 11) of the GMSL signal in the early Holocene. Extended Data Fig. 11 shows scatter in the fingerprint result (reflecting uncertainties in the GIA modelling), but also suggests that the average ratio is slowly dropping with time.

The drop in fingerprint with time may well reflect further continued early Holocene mass-centre shifting within the NAISC, from a position over central Canada to one over Greenland. The 74% ratio falls in between the GIA-modelled fingerprint of the NAISC around 14.65 ka (about 80%, meltwater pulse 1A) for the North Sea43 and the modelled fingerprint of 70% for the 8.5–8.2 ka Lake Agassiz–Ojibway drainage events in this region93. These differences are explained by the fact that for 14.65 ka the western part of the NAISC was the modelled source area (at greater distance from the North Sea), whereas for 8.5–8.2 ka, the southeastern part of the NAISC is the source area (closer to the North Sea).

This fingerprint ratio, including the 2σ range, was then used to translate the 26.3 m (2σ range, 23.8–28.8 m; 74%) residual SLR in the North Sea region to a global NAISC–AIS signal of 35.5 m (2σ range 27.1–40.0 m; 100%). Adding the EuIS contribution of 2.2 m SLE (2σ range 1.5–2.9 m; see below) after 11 ka results in a total GMSL rise of 37.7 m (2σ range, 29.3–42.2 m) between 11 ka and 3 ka (Fig. 4a). In a next iterative round of running 1D and 3D GIA models, temporal variability of the GMSL fingerprint on the North Sea residual RSL signal may be re-evaluated by tuning GIA model simulations, including an updated NAISC, to sea-level data. This should improve the match between fingerprint-corrected GMSL curves and the geological sea-level observations. Such an optimization was beyond the scope of the current work.

Additional details and references regarding the methods2,8,10,14,16,23,25,32,33,46,47,48,57,58,59,60,61,62,63,64,65,66,86,88,91,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147,148,149,150,151,152,153,154,155,156,157,158,159,160,161,162,163,164,165,166,167,168,169,170,171,172,173,174,175,176,177,178,179 are available in supplementary information49.