Background & Summary

The photosynthesis, which is dependent on solar radiation, represents a significant physiological process in vegetation. This process has a considerable impact on the global climate, particularly with regard to the global carbon cycle1,2. The portion of solar radiation in the spectrum that is effective for photosynthesis in vegetation is known as Photosynthetically Active Radiation (PAR), and its wavelength ranges from 380 nm to 710 nm. On average, PAR accounts for approximately 50% of the total solar radiation, providing the energy source for the essential processes of vegetation photosynthesis. The term Absorbed PAR (APAR) is defined as the fraction of PAR absorbed by the vegetation canopy and involved in the accumulation of photosynthetic biomass. The Fraction of Absorbed Photosynthetically Active Radiation (FPAR) is defined as the proportion of PAR absorbed by vegetation relative to the total incident solar radiation2,3,4,5. FPAR is among the 14 critical land surface parameters influencing the modeling of global climate change, as proposed by the Global Climate Observing System (GCOS)6. It is also a crucial parameter in light energy utilization models, with the accuracy of FPAR estimation directly influencing the precision of vegetation Gross Primary Productivity (GPP) and Net Primary Productivity (NPP) estimation7,8,9,10. Furthermore, FPAR is a pivotal physical quantity in other disciplines, such as climatology and ecology, where it is employed to describe biological processes on Earth. In the study of the interrelationship between human society and the vegetation and climate systems, FPAR is also a widely utilized parameter11.

Among the various global FPAR datasets, the Moderate Resolution Imaging Spectroradiometer (MODIS) FPAR product is among the most widely utilized. MODIS FPAR has the advantages of a physical-based inversion algorithm, long time series coverage, relatively accurate validation results, and straightforward accessibility12,13,14. Unlike some FPAR products, MODIS FPAR uses an inversion algorithm that does not require inputs from other FPAR or LAI products5,15. The aforementioned advantages have led numerous scholars to utilize MODIS FPAR products in the generation of training sets for machine learning or as benchmarks for intercomparison16,17,18, and MODIS FPAR has made substantial contributions to many fields of studies, including surface carbon cycling, evapotranspiration, monitoring of vegetation growth, and estimation of crop yields19.

The inversion algorithm for MODIS FPAR includes a main algorithm based on a 3-Dimensional Radiative Transfer (3D RT) model, as well as a backup algorithm that uses an empirical relationship between the Normalized Difference Vegetation Index (NDVI) and FPAR5,15,20. The main algorithm uses the 3D RT based Look-Up Table (LUT) method to simulate the photon transfer process by taking the vegetation type as a priori knowledge, and the information from several MODIS spectral bands as the input to obtain the FPAR estimations4,21. When the main algorithm fails, the backup algorithm is used to obtain FPAR values with relatively low accuracy. The best daily retrieval results are then selected during a compositing time period to create 4-day or 8-day products. Therefore, the MODIS FPAR products are independently retrieved on a pixel-by-pixel and day-by-day basis, resulting in uncertainties because FPAR retrievals on adjacent pixels and days may vary greatly due to changes in observation conditions. Specifically, atmospheric conditions including clouds, cloud shadows, and high aerosols, as well as sensor failures and inherent uncertainties in upstream product algorithms, contribute to unsatisfactory spatiotemporal consistency and time-series noises in MODIS FPAR22,23,24. This is mainly reflected in the underestimation of the backup algorithm FPAR relative to the main algorithm FPAR, which is more pronounced in the tropical regions with dense vegetation20,25,26. Fortunately, a recent study has proved that such internal inconsistency has insignificant impact on long-term vegetation trend studies25.

Uncertainties in satellite-derived FPAR datasets can significantly impact studies on ecosystem productivity and our understanding of ecosystem structure and function, leading to considerable errors in carbon and water model simulations. This challenge also affects MODIS LAI products, due to their close correlation with FPAR arising from their inversion algorithms. Over the past two decades, substantial efforts have been dedicated to improving the quality of MODIS LAI/FPAR products. The Temporal-Spatio Filtering (TSF) technique proposed by Fang addresses this issue by combining multi-seasonal mean trends with seasonal observations, creating continuous MODIS C4(Collection 4) LAI products for North America across spital and temporal. This approach aims to rectify data gaps and quality issues arising from cloud cover, seasonal snow, and instrument anomalies27. Similarly, Gao utilized TIMESAT to refine MODIS C4 products, focusing on fitting FPAR time series profiles with high-quality data while replacing less reliable or missing pixel to produce continuous LAI time series with high-quality28. The modified TSF (mTSF) method further advances this by integrating relatively low-quality data with TIMESAT and Savitzky–Golay (SG) filtering to generate improved MODIS C5 FPAR products29. However, these methods primarily address temporal information and may not fully incorporate spatial correlations, potentially smoothing out real surface anomalies such as vegetation loss from forest fires.

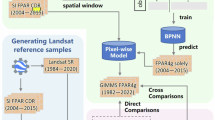
To solve the above problems, we proposed the Spatio-Temporal Information Composition Algorithm (STICA) in our previous research30 and this algorithm has been successfully implemented on the Google Earth Engine (GEE) cloud computing platform to improve the quality of MODIS LAI product31. This paper introduces the newly released MODIS reprocessed High-Quality FPAR product using the STICA algorithm and some detailed refinements (See Methods). We acquired the MODIS C6.1 FPAR dataset on GEE and generated the HiQ-FPAR dataset on a global scale for the period from 2000 to 2023. We evaluated the accuracy of HiQ-FPAR using ground truth, and then compared it with MODIS FPAR and Sensor-Independent FPAR (SI-FPAR) at a global scale and for specific biome types. We also analyzed the consistency of global FPAR interannual trends. The production process of the HiQ-FPAR product is shown in Fig. 2.

Methods

Google earth engine platform

The GEE platform, leveraging Google’s cloud computing service, offers extensive satellite imagery and geospatial datasets, enabling efficient analysis and visualization, thus conserving considerable time and computational resources in scientific research. Since our research requires global 500 m datasets every 8 days spanning 24 years, we chose GEE to solve the substantial computational demands. Furthermore, GEE helps us to easily release this high-quality product publicly and enables the provision of codes and web apps alongside ready-to-use datasets for the benefit of scientific community.

Global FPAR products

We selected the standard MODIS Collection 6.1 product (MOD15A2H) as the input FPAR data for the generation of HiQ-FPAR, which was also used for cross-comparison with HiQ-FPAR. The MOD15A2H product provides global FPAR data from 2000 to the present, featuring an 8-day temporal resolution and a 500-meter spatial resolution12,15. MOD15A2H are distributed in Standard Hierarchical Data Format (HDF) files, each containing six Scientific Datasets (SDSs). In order of appearance, these are: Fpar_500 m, Lai_500m, FparLai_QC, FparExtra_QC, FparStdDev and LaiStdDev4,12,15. In this study, we selected Fpar_500m, FparLai_QC, and FparStdDev as input data. These three SDSs include information about FPAR retrieval, algorithmic path, and retrieval uncertainty, respectively31. Typically, the MOD15A2H product has 46 composites per year, but some years may lose 1-2 composites due to sensor anomalies or other reasons (e.g., 2001, 2016, and 2022). This issue can also lead to unusual gaps in the available data (e.g., the 17th image of 2023). To address this, we used the Climatology (Clim) method to gap-fill the MOD15A2H data prior to input32.

The SI FPAR product is a sensor-independent Climate Data Record (CDR) for FPAR, derived from the standard FPAR products of Terra-MODIS, Aqua-MODIS, and VIIRS33. It spans from 2000 to 2022, offering global coverage with spatial resolutions of 500m/5 km/0.05 degrees, and temporal resolutions of 8 days or biweekly intervals. The SI FPAR CDR has significant advantages over other existing FPAR products. It is based on multiple products and employs a spatio-temporal tensor model for its generation, which means that SI FPAR almost does not generate new data; all data are high-quality retrievals from existing products. Consequently, the entire dataset is independent of any single sensor and is not affected by individual observations. The algorithm for generating SI data involves four steps: (i) filtering the raw data using QA values that screen out the image elements retrieved by the backup algorithm; (ii) merging the filtered Terra/Aqua/VIIRS FPAR into a filtered SI FPAR time series; (iii) filling the gaps of the missing values with the spatio-temporal tensor complementation model34; (iv) producing SI FPAR Climate Data Records across various projections, spatial resolutions, and temporal intervals33. In this study, we selected the 500 m spatial resolution 8-day temporal resolution SI FPAR from 2000 to 2022 for cross-comparison with other FPAR datasets and HiQ-FPAR.

Land cover type product

In this study, we utilized the MODIS Land Cover Type Product (MCD12Q1) as the biome classification map. The MODIS FPAR retrieval algorithm adjusts parameters according to different biomes to reduce uncertainty. The MCD12Q1 Version 6.1 data product is derived using supervised classifications of MODIS Terra and Aqua reflectance data. This product provides global land cover maps for the years 2001–2022, with one map per year at a spatial resolution of 500 m. Land cover types are categorized according to the International Geosphere-Biosphere Programme (IGBP), University of Maryland (UMD), Leaf Area Index (LAI), BIOME-Biogeochemical Cycles (BGC), and Plant Functional Types (PFT) classification schemes. For this study, we employed the LAI classification scheme, which includes 8 biome types: B1 (Grasslands), B2 (Shrublands), B3 (Broadleaf Croplands), B4 (Savannas), B5 (Evergreen Broadleaf Forests, EBF), B6 (Deciduous Broadleaf Forests, DBF), B7 (Evergreen Needleleaf Forests, ENF), and B8 (Deciduous Needleleaf Forests, DNF)12. A global distribution of 8 biomes in 2021 as shown in Fig. 1.

Fig. 1
figure 1

Validation site versus land cover type distribution map. Pink pentagrams and yellow dots indicate GBOV and BELMANIP 2.1 sites, respectively and background map shows the land cover type of MCD12Q1 in 2021.

Full size image

Ground FPAR reference

With the increasing availability of Earth Observation (EO) products, there has been a growing emphasis on the uncertainty assessments of these products, which are typically validated using ground measurements33. We have collected two EO products for direct comparison with HiQ-FPAR data. The Ground-Based Observations for Validation (GBOV) service is an integral part of the Copernicus Global Land Service (CGLS)35,36,37,38, delivering free access to operational data and information services in a wide range of application areas(https://gbov.acri.fr)22. GBOV provides two types of accessible data: Reference Measurements (RM) and Land Products (LP). RM are created based on raw ground measurements that have undergone stringent quality screening, whereas LP are expanded products derived from RM. Currently, GBOV offers LP datasets including TOC-R, LAI, FPAR, Fcover, Soil Moisture, and LST. In this study, we used the FPAR LP product (LP4) to directly validate HiQ-FPAR. In this study, we obtained LP4 data from the website for the period from 2013 to 2021. However, to ensure validation accuracy, we conducted subsequent quality screening. First, we masked all data records with FPAR values outside the specified range. Then, we filtered out LP data with fewer than 90% of effective pixel coverage. After processing, we obtained a total of 821 data records from 28 sites (Fig. 1). LP data observations were conducted within a 3 × 3 km area, corresponding to a 6 × 6 pixel range of 500 m resolution FPAR data. We took the average value within this range for validation.

The BEnch-mark Land Multisite ANalysis and Intercomparison of Products (BELMANIP 2.1) dataset represents a vital resource for evaluating remote sensing products, distinguished by its strategically located observation sites distributed across various latitudes and vegetation types globally. This extensive geographical and ecological span ensures comprehensive representation of diverse climatic zones and vegetation types, ranging from temperate forests to arid deserts. To enhance the dataset’s ability to represent global vegetation dynamics and climate conditions while minimizing dependence on ground-based measurements, BELMANIP 2.1 utilizes the GLOBCOVER vegetation land cover map, which is based on MERIS imagery from 200939. Site selection was meticulously executed across latitudinal bands (each 10° wide), preserving the proportional distribution of biome types within the selected sites in alignment with the broader latitudinal bands. Sites were chosen for their homogeneity over a 10 × 10 km area, with careful consideration given to minimizing urbanization and permanent water bodies. The original BELMANIP 2 dataset comprised 420 sites, whereas BELMANIP 2.1 enhances this network with an additional 25 sites that specifically represent bare soil areas (deserts) and tropical forests (Fig. 1). Given the limited availability of direct validation data, this study leverages the spatially diverse distribution of BELMANIP 2.1 sites for indirect validation of remote sensing products across different vegetation types. This approach, similar to the method used in GBOV, involves calculating the average value of FPAR within a 3 × 3 km area centered on each site, thereby providing a robust framework for evaluating the accuracy of satellite-derived metrics.

Generation of The HiQ-FPAR product

In this study, we utilized the Spatio-Temporal Information Composition Algorithm (STICA) to generate HiQ-FPAR products. Originally developed to enhance the quality of MODIS LAI data by mitigating noise, the algorithm’s versatility and the similarities between LAI and FPAR data facilitated its adaptation to improve MODIS FPAR products. Detailed algorithmic specifics can be found in Wang et al.30. Figure 2 outlines the main steps involved in producing HiQ-FPAR, which can be broadly divided into three stages:

Fig. 2
figure 2

Schematic flowchart of the generation and evaluation of the HiQ-FPAR product.

Full size image

Firstly, we conducted an uncertainty assessment of the raw MODIS FPAR product using multiple indicators, a process referred to as Multiple Quality Assessment (MQA). The indicators employed include Algorithm Path (AP), FPAR Standard Deviation (STD-FPAR), and Relative Time-Series Stability (RE-TSS). The AP, a crucial indicator, is accessible via the “FparLai_QC” layer. Numerous studies have demonstrated that the retrieval accuracy and quality of MODIS FPAR data using the main algorithm are superior. Consequently, in MQA, the main algorithm is assigned a higher score than the backup algorithm. However, the quality of retrieved pixels by the main algorithm can still vary. We categorized these pixels using STD-FPAR and RE-TSS, with STD-FPAR data available through the “FparStdDev_500m” layer and RE-TSS requiring independent calculation as detailed in “Evaluation of the HiQ-FPAR Product.” Notably, due to anomalous gaps in some MODIS FPAR imagery, we employed the Clim algorithm for gap-filling32. Pixels filled using this method were assigned scores equivalent to those of pixels retrieved by the backup algorithm in MQA.

Subsequently, we improved the data from both the spatial and temporal dimensions. The spatial dimension employed the Inverse Distance Weighted (IDW) method, performing a weighted sum of pixels within a 9 × 9 pixel window around a central pixel that shared the same biome type. The weights of the surrounding pixels were determined by their Euclidean distance from the central pixel and their MQA values, with closer pixels and those with higher MQA values receiving greater weights, resulting in spatial FPAR (FPAR_S). The temporal dimension utilized the Simple Exponential Smoothing (SES) method, performing a weighted sum of pixel values from three images before and after the central pixel’s position. The weights of the values from different images were determined by their temporal distance from the central image and their respective MQA values. This produced the temporal FPAR (FPAR_T).

To generate the HiQ-FPAR product, we synthesized the resulting FPAR_S and FPAR_T with the original MODIS FPAR. For each pixel P(x, y) at a given time, we computed relative error total sum of squares (RE-TSS) values for the three da

ta sources at the same location. As higher TSS values indicate lower data stability, we applied the inverse of these values as weights in a weighted average calculation, yielding the HiQ-FPAR values for each specific time and location.

The synthetic formula for HiQ-FPAR is shown below:

$${{HiQ}}_{{FPAR}\left(x,y\right)}=\frac{{{Fpa}{r}_{S}}_{\left(x,y\right)}\times {W}_{1}+{{Fpa}{r}_{T}}_{\left(x,y\right)}\times {W}_{2}+{{Fpa}{r}_{{Raw}}}_{\left(x,y\right)}\times {W}_{3}}{{W}_{1}+{W}_{2}+{W}_{3}}$$
(1)

where W1, W2, and W3 represent the weights of spatial, temporal, and raw LAI, respectively, which can be expressed as follows. W1, W2, and W3 are calculated as follows:

$${W}_{k}=\frac{1}{\text{relative}{{\rm{TSS}}}_{k}\left(x,y\right)},k=\left(1,2,3\right)$$
(2)

where relative TSSk(x, y) represents the fluctuation of the time series at pixel (x, y). This process was repeated to generate a global HiQ-FPAR dataset for the years 2000 to 2023: The final HiQ-FPAR product consists of four layers: FPAR, FPAR_QC, Re_TSS_Overall, and Fpar_Diff. It should be noted that the ‘FPAR_QC’ layer here is not a newly produced QC layer, but the original layer of MODIS FPAR. The MQA layers obtained in the algorithm were not put into the result due to the file size limitation, but they can be obtained by modifying the code in the algorithmic code we made public. For more information on these layers, see the ‘Data Records’ section.

The resulting HiQ-FPAR product exhibits improved spatial and temporal reliability and consistency compared to the raw product. Notably, STICA relies exclusively on MODIS data, avoiding the additional uncertainties associated with integrating multiple data sources. In contrast, the new released Sensor Independent (SI) FPAR product employs a spatiotemporal tensor model, which primarily addresses quality by replacing lower quality data with higher quality data from other sensors. This approach, however, does not fully resolve the inconsistencies inherent in different products, leading to suboptimal consistency in the final SI FPAR.

Evaluation of the HiQ-FPAR product

The evaluation of the HiQ-FPAR product involved three components: direct validation against ground FPAR reference values, cross-validation with other FPAR products, and trend analysis and Temporal Series Stability (TSS) calculation.

Direct validation

For direct validation, we utilized GBOV data from 2013 to 2021 to validate MODIS FPAR, HiQ-FPAR, and SI FPAR products. The accuracy of these FPAR datasets was assessed by calculating the R2 and RMSE values between the reference values at 28 sites and the three types of FPAR data. For these calculations, the average values within a 3×3 km area centered on the site coordinates were used as reference values for the three FPAR datasets. It is noteworthy that the BELMANIP dataset was not used for direct validation due to the limited availability of reference values.

Cross-validation

We evaluated the consistency between HiQ-FPAR and other FPAR products (MODIS FPAR and SI FPAR). Initially, we generated global distribution maps of the MODIS FPAR, HiQ-FPAR, and SI FPAR products and aggregated their distributions by latitude at a 0.05° resolution. To observe the similarities and differences over a long time series, we plotted the latitude-averaged time series of the three products from 2001 to 2022 for qualitative analysis. Subsequently, we used BELMANIP sites and land cover data to analyze the performance of the three datasets across different vegetation types. Finally, we selected 46 images within a year and computed the R2, RMSE, and MAE values between HiQ-FPAR and the other two FPAR datasets on a pixel-by-pixel basis to assess their consistency.

Trend analysis and Time-Series Stability (TSS) calculation

The annual average trends (2001–2022) of MODIS FPAR, HiQ-FPAR, and SI FPAR were assessed using the Theil-Sen slope (TS) method and validated with the Mann-Kendall (MK) test. The TS method calculates the slope by pairing data points over the time range and then taking the median of all these pairwise slopes as the trend for the dataset during the period. This approach reduces the impact of outliers compared to some common regression methods. The MK test evaluates the significance of the trend calculated by the TS method, determining whether the observed trend is statistically significant. Together, these methods are used to examine the trend distribution of long-term FPAR data on a global scale. The specific calculation formulas are as follows:

$${TS}={\rm{median}}\left(\frac{{X}_{j}-{X}_{i}}{j-i}\right),2001\le i < j\le 2022$$
(3)

Here \({x}_{i}\) and \({x}_{j}\) represent the FPAR values for years i and j respectively, TS > 0 indicates an increasing trend, whereas TS ≤ 0 indicates a decreasing trend.

$$S={\sum }_{i=1}^{n-1}\mathop{\sum }\limits_{j=i+1}^{n}\mathrm{sgn}\left({x}_{j}-{x}_{i}\right)$$
(4)

To compute the Mann-Kendall test statistic S, the formula employs the sign function \(\mathrm{sgn}({\rm{x}})\), where \(n\) denotes the number of time series observations, and \({x}_{i}\) and \({x}_{j}\) represent the data values.

$${\rm{Var}}\left(S\right)=\frac{n\left(n-1\right)\left(2n+5\right)-\mathop{\sum }\limits_{i=1}^{m}{t}_{i}\left({t}_{i}-1\right)\left(2{t}_{i}+5\right)}{18}$$
(5)

Here m denotes the counts of successive groups in the data (repeated dataset), and ti denotes the correlation counts (number of times it is repeated in the i-th range). In the case of large samples, the S approximately obeys a normal distribution and the Zs is calculated as:

$${{\rm{Z}}}_{{\rm{s}}}=\left\{\begin{array}{ccc}\frac{{\rm{S}}-1}{\sqrt{{\rm{Var}}\left({\rm{S}}\right)}}, & \text{if} & {\rm{S}} > 0\\ 0 & \text{if} & {\rm{S}}=0\\ \frac{{\rm{S}}+1}{\sqrt{{\rm{Var}}\left({\rm{S}}\right)}}, & \text{if} & {\rm{S}} < 0\end{array}\right.$$
(6)

Based on the calculated Zs, the significance of the trend can be determined by looking up the standard normal distribution table. When \({{\rm{|Z}}}_{{\rm{s}}}|\)>\({{\rm{Z}}}_{1-{\rm{\alpha }}/2}\), it can be seen as a rejection of the null hypothesis that there is a significant trend in this data set. Therefore, different values of α will give different results of trend test and in this study α = 0.05, i.e. \({{\rm{Z}}}_{1-{\rm{\alpha }}/2}\) = 1.96 is used as the criterion.

Time-Series Stability (TSS) measures the deviation of a value at a specific time from the linear interpolation of values at adjacent times. In this study, we calculated the cumulative TSS over one year for three types of data: MODIS FPAR, HiQ-FPAR, and SI FPAR. Higher TSS values indicate lower temporal stability of the data. TSS is calculated as follows:

$${\rm{TSS}}\left(t\right)=\frac{\left|\begin{array}{c}\left(X\left({t}_{n+1}\right)-X\left({t}_{n-1}\right)\right)\times {t}_{n}-X\left({t}_{n}\right)\times \left({t}_{n+1}-{t}_{n-1}\right)-\\ \left(X\left({t}_{n+1}\right)-X\left({t}_{n-1}\right)\right)\times {t}_{n-1}+X\left({t}_{n-1}\right)\times \left({t}_{n+1}-{t}_{n-1}\right)\end{array}\right|}{\sqrt{{\left(X\left({t}_{n+1}\right)-X\left({t}_{n-1}\right)\right)}^{2}-{\left({t}_{n+1}-{t}_{n-1}\right)}^{2}}}$$
(7)

where \(X\left({t}_{n-1}\right)\), \(X\left({t}_{n}\right)\) and \(X\left({t}_{n+1}\right)\) represent the FPAR data at three distinct points in time within a time series: the past (\({t}_{n-1}\)), the current (\({t}_{n}\)), and the future (\({t}_{n+1}\)), respectively.

Data Records

The dataset is available at Zenodo40, and the data offers 4 Scientific Datasets: FPAR, original quality control information, relative temporal stability of HiQ-FPAR, and the absolute difference between HiQ-FPAR and MODIS FPAR. To address considerations regarding data storage size, the original values have been adjusted to integers. Users are advised to refer to the scaling factors provided in Table 1 for value restoration when utilizing the data.

Table 1 Scientific Datasets included in the HiQ-FPAR Product.
Full size table

The HiQ-FPAR is available in two projections of different spatial resolutions. Datasets at 500 m were stored in Google Earth Engine for users to mix and match with other datasets and the availability of this dataset in the GEE platform would significantly benefit the GEE community, fostering easier access and utilization of this valuable resource. A 5 km projection of HiQ-FPAR was derived by upscaling the original 500 m data using the nearest-neighbour method can be found in Zenodo40. For specific dataset descriptions and usage, please refer to our github repository(https://github.com/Gardenias-123/HiQ-FPAR).

The HiQ-FPAR product file name follows certain naming convention, providing useful information about a specific product. For example, the filename HiQ_FPAR_WGS84_5 km_8day_2022361.tif indicates:

  • HiQ: Product Short Name

  • FPAR: Land Surface Type

  • WGS84: Projection Information.

  • 5km: Spatial Resolution

  • 8day: Temporal Resolution

  • 2022361: Julian Date of Acquisition (YYYYDDD), DDD = DOY (Day of Year)

  • .tif: Data Format

Technical Validation

Direct validation based on ground FPAR reference

Ground-based FPAR observations from 29 GBOV sites, spanning the period from 2013 to 2021, were used to validate three FPAR products: MODIS FPAR, HiQ-FPAR, and SI FPAR. Figure 3 illustrates representative time series distributions of the three products alongside ground reference values. We calculated this result on the GEE platform. The results reveal a high degree of consistency between the newly developed HiQ-FPAR product and ground measurements, with overall R2/RMSE values of 0.722/0.13, substantially outperforming those of MODIS FPAR (0.63/0.154) and SI FPAR (0.717/0.146). Table 2 further presents the R² and RMSE values for three products on each site. HiQ-FPAR exhibits superior R2 and RMSE values compared to MODIS FPAR, indicating significant improvements in data accuracy due to the STICA algorithm. It should be noted that for certain sites (MOAB, STER, VASN, and WOMB), R2 and RMSE values were not computed due to insufficient validation data. The time series plots (Fig. 3) demonstrate seasonal variation curves across all three FPAR products. Notably, HiQ-FPAR effectively smooths the erratic fluctuations observed in MODIS FPAR, which are attributed to adverse weather conditions or sensor anomalies, thereby providing a more accurate reflection of actual phenological changes. While SI FPAR also mitigates anomalous curves by incorporating data from additional sources, it tends to overestimate at certain sites. In summary, HiQ-FPAR exhibits a clear advantage in maintaining consistency with ground-based measurements, offering a more reliable and accurate representation of FPAR dynamics. This underscores the potential of HiQ-FPAR in enhancing vegetation monitoring and ecological research.

Fig. 3
figure 3

Distribution of selected GBOV sites with three product time series from 2013–2021. The pink, blue, and earthy yellow curves represent the MODIS FPAR, HiQ-FPAR, and SI FPAR, respectively; the green dots represent GBOV observations.

Full size image
Table 2 Comparison of MODIS FPAR, HiQ-FPAR and SI FPAR over GBOV sites.
Full size table

Global spatial distribution comparison

To better observe the spatial distribution similarities and differences among MODIS FPAR, HiQ-FPAR, and SI FPAR, we generated annual mean distribution maps for the year 2021 for each product (Fig. 4a–c) and their corresponding latitudinal distribution curves (Fig. 4d). Due to the large data volume at the original 500 m resolution, we upscaled to a 5 km resolution using the nearest neighbor method. Overall, HiQ-FPAR and MODIS FPAR exhibit similar spatial distribution patterns. The latitudinal distribution curves show that HiQ-FPAR maintains consistency with MODIS FPAR, indicating that the spatial patterns of the raw MODIS data were preserved through the STICA algorithm enhancements. The standard deviation of HiQ-FPAR (orange shading in Fig. 4d) consistently aligns with that of MODIS FPAR (blue shading in Fig. 4d), highlighting HiQ-FPAR’s superior global stability. This indicates that HiQ-FPAR data is of higher quality and stability. Conversely, SI FPAR shows higher values in the Amazon region, central and western Africa, and Siberia compared to MODIS and HiQ-FPAR. The latitudinal distribution curves also reveal that SI FPAR values are noticeably higher at the equator and in the high northern latitudes (above 60°N). Discrepancies may arise as the SI FPAR dataset leverages a main algorithm merging strategy, whereby pixels initially generated via backup algorithms are substituted with outputs from the main algorithms of alternative data sources. This approach effectively reduces potential biases introduced by cloud or aerosol interference. However, in contrast to HiQ and MODIS, the SI dataset employs fewer backup algorithms, which may introduce bias under challenging observational conditions. For instance, in densely vegetated regions (e.g., near 0° and 60°N), SI FPAR values tend to be elevated25. Although this methodology improves data continuity and consistency, it may result in some variations when compared with other datasets in high-vegetation regions.

Fig. 4
figure 4

Global spatial distribution of the mean HiQ-FPAR (a), MODIS FPAR (b), and SI FPAR (c) for all 46 images in 2021, along with the latitude distribution (d). In panel (d), the latitude interval is 0.05°, and the lines represent MODIS FPAR (blue), HiQ-FPAR (orange), and SI FPAR (green).

Full size image

Hovmöller plots were employed to qualitatively analyze the temporal variations of these three long-term FPAR products across different latitudinal bands in Fig. 5. These plots reveal distinct seasonal FPAR patterns between the Southern and Northern Hemispheres. Notably, the highest mean FPAR values are observed at the equator, with a secondary peak evident during the growing season in the northern high latitudes.

Fig. 5
figure 5

Hovmöller diagrams of the mean values of the (a) MODIS FPAR, (b) SI FPAR and (c) HiQ-FPAR for latitudinal bands during 2001–2021.

Full size image

Overall, HiQ-FPAR exhibits a pattern that closely mirrors MODIS FPAR, albeit with a significantly smoother temporal profile, effectively reducing some of the noise present in the MODIS data. HiQ-FPAR values are slightly higher at the equator and during the growing season in the northern high latitudes. In contrast, SI FPAR shows considerable divergence from both MODIS and HiQ-FPAR. Specifically, SI FPAR values are typically higher than the other two products at high latitudes in the summer, while the same latitudes have significantly lower SI FPAR values in the winter. This result aligns with the pattern observed in Fig. 4. The original MODIS FPAR product, due to observational constraints, contains a considerable number of FPAR values retrieved by backup algorithms. As HiQ-FPAR also uses MODIS FPAR as its base data, both products retain a significant proportion of backup algorithm outputs. In contrast, SI FPAR largely retains values retrieved by the main algorithm, which may contribute to relatively higher FPAR values in tropical regions and during the growing season at higher latitudes.

Biome specific comparison

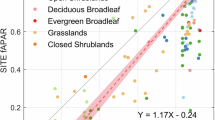
To assess the performance of HiQ-FPAR across different biome types, we extracted MODIS FPAR, HiQ-FPAR, and SI FPAR values from the BELMANIP V2.1 sites. We performed cross-validation of these products across seven distinct vegetation types (B1–B7) and mixed pixel types by computing R2 and RMSE values, as detailed in Table 3. Additionally, we generated scatter plots (Fig. 6) to evaluate the consistency among the products.

Table 3 Cross Comparison of MODIS FPAR, HiQ-FPAR and SI FPAR across Biome type.
Full size table
Fig. 6
figure 6

Cross-comparison scatterplots of the three products in 2021 (based on BELMANIP 2.1 site). (a–c) represent the validation scatter plots for HiQ-MODIS, HiQ-SI, and MODIS-SI, respectively. The red line denotes the fitted line and the black dashed line is the 1:1 split line. The color of the scatter indicates the density of the points.

Full size image

The results reveal that, with the exception of B5, HiQ-FPAR and MODIS FPAR show strong agreement across the remaining six vegetation types, with R2 values exceeding 0.84. The agreement for mixed pixels is also robust, with an R2 of 0.87 and an RMSE of 0.09. However, a notable discrepancy is observed in the B5 vegetation type, with an R2 of only 0.73 and an RMSE of 0.13. The B5 biome, predominantly found in the Amazon rainforest regions of South America, Indonesia, and Central Africa (Fig. 1), faces persistent issues such as high cloud cover, elevated aerosol concentrations, and NIR saturation. These factors lead to limited high-quality observations and less accurate FPAR inversions, necessitating reliance on backup algorithm retrievals and contributing to the observed discrepancies.

As can be seen from the results, HiQ-FPAR and MODIS FPAR show consistency over most areas and vegetation types, with differences mainly in areas affected by quality issues. This inconsistency was more pronounced in the validation of the SI FPAR against the other two datasets, especially in the B5 biome. As shown in Fig. 5(b,c), many of the scatters are horizontally distributed (highlighted with orange ellipses), indicating that the SI FPAR values are significantly higher than the other two FPAR values.The higher uncertainty in SI FPAR is attributed to the fact that on some pixels it replaces the original image values with values obtained by the main algorithms of the other products, and that many of these replaced pixels are distributed in the B5 region, whereas the values that are replaced in the B5 region are usually higher than the original observed FPAR values12,13,41. The position of the scatter in relation to the 1:1 line (black dashed line in Fig. 5) further reveals that the HiQ-FPAR values are generally slightly higher than the MODIS FPAR, while the SI FPAR values are a little bit more skewed in comparison to both other products.

Analyzing the performance of MODIS FPAR, HiQ-FPAR, and SI FPAR across different biomes using only selected sites can be insufficient. Therefore, we generated distribution histograms for the three products in 2021 based on eight vegetation types (B1-B8) (Fig. 7) to evaluate these products globally. The results align with the conclusions from (Fig. 6), showing that the most significant discrepancies among the three products occur in B5, followed by B2. SI FPAR exhibits more pronounced differences compared to the other two FPAR products.

Fig. 7
figure 7

Histograms of MODIS, HiQ and SI FPAR data by vegetation type. The broken line represents the histogram of the FPAR distribution, and the dashed line represents the mean. Pink, green and earthy yellow colours indicate MODIS FPAR, HiQ-FPAR and SI FPAR products, respectively.

Full size image

Global trend comparison

To compare global vegetation trends across the MODIS FPAR, HiQ-FPAR, and SI FPAR products, we calculated annual mean FPAR values from 2000 to 2023. We then fitted the time series to determine the slope and applied the Mann-Kendall (MK) test to assess the significance of these trends, resulting in a spatial trend change map for the period (Fig. 8). This map highlights regions with significant greening (positive slope) or browning (negative slope) trends, offering crucial insights into global vegetation dynamics.

Fig. 8
figure 8

Plot of global FPAR trends between MODIS FPAR (a), HiQ-FPAR (b) and SI FPAR(c) for the period 2000–2023. Only significantly changing pixels are plotted on this map; the grey parts are land with vegetation cover but not significant changes, the white parts are unvegetated land such as deserts, glaciers, permanent snow, etc., and the blue parts are bodies of water.

Full size image

Each of the three products indicates comparable spatial patterns of greening, particularly in key regions like China and India, and similarly detects browning trends in similar areas. Specifically, MODIS FPAR and HiQ-FPAR demonstrate highly congruent trends, with 70% of the image elements showing no significant change in either product. Of the remaining elements, MODIS FPAR indicates a greening trend in 26%, while HiQ-FPAR shows 25%. The SI FPAR results exhibit slight differences, with 61% of the image elements showing no significant trend and 31% indicating a greening trend, which aligns reasonably with the overall patterns. Overall, the trends across the three products are broadly consistent, with minor variations primarily observed at high latitudes in the northern hemisphere. This result also shows that although SI FPAR is slightly higher than MODIS FPAR and HiQ-FPAR in some areas due to the predominance of the values retrieved by the main algorithm, this does not have a significant effect on the long-term vegetation trends, which is also in line with the results of Zhang et al.25.

Global time-series stability comparison

FPAR typically exhibits continuous annual variation without significant fluctuations42. However, the seasonal variation curve of MODIS FPAR often displays notable anomalies, such as abrupt increases and decreases. These irregularities stem from MODIS FPAR’s pixel-by-pixel, day-by-day retrieval process, which, influenced by atmospheric conditions, sensor malfunctions, and algorithm uncertainties31, leads to reduced temporal and spatial coherence and increased noise levels14,43. Consequently, MODIS FPAR struggles to accurately capture long-term FPAR trends, limiting its effectiveness for crop modelling, climate change studies, vegetation dynamics analysis, and long-term ecosystem monitoring44,45,46,47,48,49,50.

As evidenced by the direct ground validation results (Fig. 3), HiQ-FPAR substantially enhances the data quality of raw MODIS FPAR. It mitigates significant errors in raw FPAR extraction and produces smoother FPAR time series profiles that align more closely with expected phenological patterns. Nevertheless, due to spatial scale and resource constraints, GBOV site data alone are insufficient for a comprehensive global comparison of temporal changes. To address this, we employed TSS, a quantitative indicator of time-series stability, to further assess the temporal stability of the two products42. HiQ-FPAR exhibits a higher proportion of smaller TSS values (Fig. 9), especially in equatorial regions dominated by EBF vegetation. The global proportion of low TSS values increased from 44.2% in MODIS to 76.9% in HiQ, indicating a significant improvement in time-series stability in the HiQ-FPAR product compared to the raw MODIS FPAR. This enhancement elevates overall data quality, providing more reliable support for research and applications in ecology, climatology, and land use planning. Additionally, SI FPAR also demonstrates improved temporal stability over MODIS FPAR due to its spatio-temporal tensor processing, with a TSS distribution closely resembling that of HiQ-FPAR.

Fig. 9
figure 9

Cumulative RE-TSS distribution for the full year 2021 for the three products (46 images). (a–c) represent MODIS FPAR, HiQ-FPAR, and SI FPAR products, respectively.

Full size image

Moreover, the main algorithm used in SI FPAR tends to exhibit systematic biases, with retrieved pixel values often being slightly higher than those of HiQ-FPAR and MODIS FPAR in certain areas. Despite its limitations, SI FPAR has its own merits. Its calculation process is based entirely on existing product data, thus avoiding errors associated with human intervention

Consistency testing on a global scale

In the preceding section, we assessed the FPAR data from the three products around specific sites for validation. However, this approach does not fully capture the global-scale consistency among the products. To address this, we analyzed the consistency between HiQ-FPAR and the other two products across a 46-period image in 2021.

We computed the correlation coefficient (R), mean absolute error (MAE), and RMSE values for each image element of the 46-period image, comparing HiQ-FPAR with the other two products. These values were normalized to a range of 0–255 and visualized using an RGB color composite, where RMSE was represented in red, R in blue, and MAE in green to create a global consistency map (Fig. 10). In this visualization, bluer colors indicate higher R values, and lower MAE and RMSE, reflecting better consistency; conversely, yellowish colors signify lower R values and higher MAE and RMSE, indicating poorer consistency.

Fig. 10
figure 10

Agreement of HiQ-FPAR with MODIS-FPAR and SI-FPAR in 2021(containing 46 data periods). The blue image elements in both plots are in better agreement and the yellow is in worse agreement.

Full size image

The results reveal that HiQ-FPAR exhibits generally high consistency with MODIS FPAR, though there are notable exceptions in regions such as the Amazon, Central Africa, and South Asia, where the consistency is poorer. In contrast, HiQ-FPAR shows less agreement with SI FPAR, with many pixels appearing light blue or white. This suggests that areas with poor consistency with MODIS FPAR also exhibit poor consistency with SI FPAR. This discrepancy may be attributed to HiQ-FPAR’s reliance solely on MODIS data, whereas SI FPAR incorporates a broader range of data sources, highlighting the inherent inconsistencies among different data sources.

Usage Notes

In addition to the repository data, our dataset is also available for users to download and visualise at GEE. The dataset links are as follows:

  1. 1.

    https://code.earthengine.google.com/?asset=projects/verselab-398313/assets/HiQ_Fpar/wgs_500m_8d (spatial resolution is 500m and temporal resolution is 8 days)

  2. 2.

    https://code.earthengine.google.com/?asset=projects/verselab-398313/assets/HiQ_Fpar/wgs_5km_8d_Bicubic (spatial resolution is 5km and temporal resolution is 8 days)

Before using our data (HiQ-FPAR), we offer some suggestions for you. First, there is the issue of the spatial and temporal resolution of the data. The data we are currently providing are global FPAR data with 8-day resolution, and there are two kinds of spatial resolution, 500 m and 5000 m. The 500 m data is the most complete data with various layers, including quality control layer, TSS layer and difference layer. With these auxiliary layers, the data can be better analyzed. Of course, if you need to download many years of data quickly or don’t have enough storage space, you can also download the 5 km resolution data, but these data are only available in the FPAR band. You can also choose to resample the data. Nearest neighbour sampling is available on Zenodo, and bicubic sampling is available on GEE. The second thing is to pay attention to the quality control layer when using the data. Due to the special way of MODIS inversion, its main algorithm and backup algorithm produce data with poor consistency. Please make sure to refer to our quality control layer when your research requires strict quality control. Detailed usage instructions are available in the GitHub repository (https://github.com/Gardenias-123/HiQ-FPAR).

For users requiring coarser spatial resolution or alternative access methods, a 5 km resolution version of the HiQ-FPAR dataset is available on Zenodo (https://zenodo.org/records/10683549)40. Annual data are provided as compressed .7z files, with each file containing all images for a given year. For instance, to obtain data for June–August 2023, users may download the 2023.7z file, extract its contents using decompression tools (e.g., Bandizip or 7.zip), and isolate the relevant time period for further analysis.

Due to file size constraints, Zenodo hosts only a subset of the 500 m resolution data. Specifically, a time-averaged product spanning 24 years, comprising 46 global images of the “Fpar” layer, is available for download as All_mean_500m.7z. However, for full-resolution 500 m HiQ-FPAR data, we recommend accessing and processing the dataset directly via GEE to facilitate research requiring higher spatial fidelity.

We note that current HiQ-FPAR product also has some limitations. It relies solely on MODIS data, which can result in large spatiotemporal gaps during sensor anomalies and limits its effectiveness in filling these gaps. Thus, while HiQ-FPAR significantly improves data accuracy, particularly in regions with consistent MODIS coverage, it remains not flawless. Continued development and refinement are needed to address these limitations and to enhance overall data quality.