Background & Summary

Distributed acoustic sensing (DAS) systems are increasingly being improved and deployed across a wide range of industries1, primarily for perimeter protection2, surroundings of submarine cables monitoring3. Futhermore, overseeing transport infrastructures such as bridges4,5, railways6,7,8, and tunnels9,10. Key performance parameters of DAS include SNR (Signal-to-Noise Ratio), measurable distance, and spatial resolution11. To enhance these parameters, algorithms are developed and tested to improve SNR2,12, anomaly detection and their classification13, and enable machine learning-based classification14,15. Datasets from DAS systems are often not available or are cropped in different ways, which makes it difficult to process them. For this purpose, a dataset16 containing acoustic vibration patterns recorded by a commercial DAS system was assembled.

The dataset contains essential data for quantifying the sensitivity of various types of cables to acoustic vibrations. In our study17, cables were exposed to acoustic vibrations in an anechoic chamber to test the feasibility of vibration sensing using an interferometric system under ideal conditions. This dataset serves as a valuable resource for researchers focusing on security issues related to eavesdropping on fiber and cable systems. To address this concern, an experimental setup was created in a common room environment to simulate realistic conditions and verify eavesdropping using a DAS reflectometric system.

Furthermore, due to its inherently noisy nature, the dataset is suitable for testing de-noising techniques or methods to enhance speech intelligibility. By evaluating the speech transmission index (STI) before and after processing, researchers can evaluate the effectiveness of their methods. The Matlab script referenced in Zaviska et al.18 can be used for STI calculation, enabling researchers to quantify speech intelligibility improvements achieved through their de-noising methods.

Methods

Distributed acoustic sensing

The Rayleigh backscattering technique, known as optical time-domain reflectometry (OTDR), has been known for decades and its history dates back to the 1980s19. The principle of OTDR is to send a pulse of optical radiation with high power into the sensed fiber. This pulse is then reflected along the entire length of the fiber.

Based on the back-reflected signal intensity and the time delay, the attenuation characteristic of the fiber can be measured and its length determined. The back-reflections are then captured by the photodetector (PD), stored in time-series and averaged. The principle of Rayleigh scattering can be seen in Fig. 1.

Fig. 1
figure 1

The principle of OTDR, based on Rayleigh backscattering.

Full size image

Rather than measuring fiber characteristics, phase-sensitive optical time-domain reflectometry (Φ-OTDR) focuses on changes in phase shift in backscattered light caused by ambient effects. Assuming that the internal structure of the fibers does not change (which can be assumed in the rest state), the vibrations in the vicinity of the fiber can be sensed using Φ-OTDR, since the structure remains unchanged, but is affected by surrounding environmental influences. As stated in the paper20,21,22, to generate signals, it is necessary to use highly coherent radiation using a narrowband laser. To generate pulses, it is required to use an optical modulator (OM) and a signal generator. Since the fiber itself can be up to several hundred kilometers long, an erbium-doped fiber amplifier (EDFA), or other type of optical amplifier, is often used to increase the power of the optical radiation. EDFA produces noise during amplification, which should be filtered out if possible, as reported by22. It is also possible to use the EDFA as a preamplifier, which amplifies the power of the reflected signal20, or to use EDFA as a booster to amplify pulses. The signal is then sampled using an analog-to-digital converter (ADC) and finally processed.

The Optasense ODH-F provides distributed acoustic measurements. Applications are mainly focused on structural monitoring in distribution pipelines, perimeter security, etc. The system has a measurement range of 10 km in phase measurement mode (P9) and up to 50 km for the intensity measurement mode single pulse (SP1), as can bee seen in Table 1. It can work with up to four connected fibers thanks to an integrated optical switch.

Table 1 Basic parameters of the Optasense ODH-F system.
Full size table

The system consists of two parts – an interrogator and a post-processing unit. Four small form-factor pluggable (SFP) positions are available to control the interrogator and retrieve measured data. The system is developed by the OptaSense DxS operating software, which enables in-depth analysis of acquired data using appropriate algorithms.

Single pulse 1 mode

SP1 mode, also referred to as ODH 2 mode, is characterized by the generation of a single pulse. In this mode, only amplitude data are captured, and this data are recorded directly as they are received from the ADC without any additional processing on phase reconstruction. This mode is characterized by a spatial resolution (SR) of 1.5 meters and an optical channel pinch (OCP) of 1, indicating that every meter along the fiber corresponds to a data sampling point.

SR of 1 in the SP mode implies that the system can detect changes over a minimum distance of one meter along the fiber. Such high resolution is particularly valuable in applications requiring the detection of fine details, and small variations in acoustic signals is crucial. On the other hand, the OCP of 1, indicates the spatial frequency at which data points are sampled along the fiber, further emphasizing the high-resolution nature of this mode. Therefore, the spatial frequency is 1/m (or 1 Hz in spatial terms).

Expanding on this, the primary focus of the SP mode is to capture the raw, unprocessed acoustic signals as they interact with the optical fiber. The use of a single pulse in this mode allows for a straightforward and direct measurement of acoustic events along the fiber. However, the amplitude response is nonlinear and less reliable for accurate signal reconstruction.

In applications where capturing the most detailed and unaltered acoustic information is necessary, the SP mode is highly advantageous. It is particularly suited for environments where the precision of acoustic event localization and the integrity of signal data are paramount. However, the trade-off for this high level of detail is the larger volume of data generated, which may require more substantial storage and processing capabilities.

Phase 9 mode

In Phase (P9) mode, the DAS system generates dual optical pulses and utilizes the concept of gauge length, which defines the fiber segment over which the pulses are offset and phase changes are detected. This mode includes a conversion from rectangular (I/Q) to polar (R/Θ) coordinates, referred to as the R-to-P transformation, which enables precise detection of phase variations induced by external vibrations. The signal is recorded after passing through the R-to-P filter, and the OCP is set to 1, meaning the system samples data at 1-meter intervals along the fiber, providing high spatial resolution.

This high resolution is particularly advantageous for applications that require detailed phase information and accurate localization of dynamic events along the fiber. The gauge length effectively controls the resolution of phase change detection; adjusting it allows tuning of the system sensitivity across different spatial scales, which is especially useful in varied sensing environments.

Phase mode is part of the system’s demodulation chain and includes several key signal processing steps, see Fig. 2: raw data signal, high-pass filtering (HPF0), digital down-conversion (DDC), low-pass filtering (LPF1), and finally, the R-to-P conversion with phase unwrapping. This processing chain enables the extraction of continuous phase signals from the raw backscattered data. P9 outputs one channel per spatial location (locus), providing a 1-channel resolution. Although primarily intended for system diagnostics and development, this mode offers a detailed, zoomed-in view of phase response and is valuable for engineering-level analysis, as stated by the manufacturer.

Fig. 2
figure 2

Diagram of the processing chain from data from ADC to data type 9.

Full size image

Overall, the phase mode is particularly suited for scenarios where detecting subtle phase shifts is critical, such as in structural health monitoring or seismic activity detection. The ability to capture phase changes with high accuracy makes this mode valuable in applications where understanding small changes in the physical environment is crucial.

Acoustic part

The Audio Precision APx525 analyzer was used for the measurement, with one channel driven by the reference microphone used to compensate for the frequency response of the measurement system and the propagation of sound waves through the acoustic environment. The device can be seen in Fig. 3.

Fig. 3
figure 3

The APx analyzer with the amplifier is on the left side, and the measurement room contains a loudspeaker, microphone and an optical cable in a plastic rail.

Full size image

All measurements were done in a closed loop with the analyzer in sync with the generator. Compensation for the dependence of sound pressure on frequency due to the response of the loudspeaker, room modes, and attenuation of the sound wave during its propagation was made possible using the B&K Type 4190 measurement microphone. The microphone was placed in the plastic rail as close as possible to the optical cable without contact with the cable. The Event 20/20 loudspeaker system was used to generate the sound wave. The loudspeaker system was placed at the height of the mouth of a standing person, with its reference axis at 1.75 m and the reference point 1.5 m from the side wall. There was a distance of 1.94 cm between the microphone and the reference point of the loudspeaker system. During measurement, three sound pressure levels of 54, 60, and 66 dB(A) were used, corresponding to levels of “relaxed”, “normal”, and “raised” speech, respectively.

Measurement setup

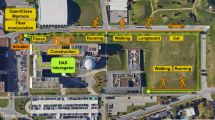
The setup, shown in Fig. 4, is made up of three routes (short, long, server). The short route is used to directly capture the sound from the loudspeaker, which is aimed towards the wall where the fiber is placed. The long route consists of a short route that is connected to the opposite wall for the ability to capture both the signal acting on the fiber optic cable and the echo signal. The last is the server route, which consists of a short route connected to the next-door room where the server room is located. The reason for this is to add additive noise to the path that may be present in common office buildings. All routes are then connected from the hallway by a patch to the next room with all the measuring equipment from where the measurements were taken. The patch was permanently connected to the cable that leads to the hallway, and all interconnection took place only in room 5.36. The DAS is linked to the measurement room from the server room, so it is possible to find occasional anomalies in the dataset caused by normal building traffic.

Fig. 4
figure 4

Diagram of the cables in the room where the loudspeaker is located.

Full size image

Measurement of background noise

Measurement of background noise consists of a short measurement (20–30 s) of the sound field when the loudspeaker system is switched off. It is used to assess the baseline noise levels of the room and the measurement system, and is applicable to de-noising methods as well as other post-processing techniques.

Swept sine signal

To characterize the sensing abilities of different setups/systems, the exponential sine signal (see Fig. 5) can be used to determine the frequency response of the entire system \({f}_{{\mathbb{S}}}\) (in this context, “system” refers to the combination of the environment, fiber/cable, and the measurement apparatus under investigation). If s(t) is a source sweep signal and c(t) is the captured signal transmitted by the system \({\mathbb{S}}\), then \({f}_{{\mathbb{S}}}={\mathsf{F}}(c)/{\mathsf{F}}(s)\), where \({\mathsf{F}}\) denotes the Fourier transform23,24,25. Even in the case where the source signal is not precisely known, the response can be computed using the measurement with the reference microphone and the corresponding impulse response provided by the APx analyzer that uses the technique presented in23. In particular, microphone recording of the swept-sine signal, m(t), and an impulse response of the speaker-environment-microphone system \({\mathbb{M}}\), \({h}_{{\mathbb{M}}}\), are available. The impulse response is related to the frequency response as \({f}_{{\mathbb{M}}}={\mathsf{F}}({h}_{{\mathbb{M}}})\)26. At the same time, the frequency response of the system \({\mathbb{M}}\) is from definition \({f}_{{\mathbb{M}}}={\mathsf{F}}(m)/{\mathsf{F}}(s)\), which is equivalent to \({\mathsf{F}}(s)={\mathsf{F}}(m)/{f}_{{\mathbb{M}}}\). Using the available outputs of the APx analyzer, we get the expression

$${f}_{{\mathbb{S}}}=\frac{{\mathsf{F}}(c)}{{\mathsf{F}}(s)}=\frac{{\mathsf{F}}(c)}{{\mathsf{F}}(m)/{f}_{{\mathbb{M}}}}=\frac{{\mathsf{F}}(c)}{{\mathsf{F}}(m)}\cdot {\mathsf{F}}({h}_{{\mathbb{M}}}).$$
(1)

Eq. (1) can be also seen as compensation or equalization of the frequency response of the loudspeaker and the attenuation during the propagation of the acoustic wave from the loudspeaker to the cable (the term \({\mathsf{F}}({h}_{{\mathbb{M}}})\)) to obtain the frequency response of propagation in the cable to the fiber core (\({\mathsf{F}}(c)/{\mathsf{F}}(m)\)).

Fig. 5
figure 5

Source signal for the swept sine measurement, shown in time domain (top) and in spectrogram (bottom).

Full size image

Although the frequency response provides an exhaustive description of the sensitivity as a function of frequency based on a very fast measurement (the length of the swept sine signal used was 2.8 s and covers the frequency range from 20 Hz up to 20 kHz), it has several drawbacks in this case:

  • The method is very sensitive to noise.

  • The procedure described above and summarized by Eq. (1) covers also the frequency-dependent properties of the loudspeaker as part of the system. This may be regarded as an undesirable interference.

  • A broad range of frequencies is covered, but there is only a limited space to focus on a particular range where the optical fibers are sensitive.

The sub-steps are described in detail in paper17. The limited sensitivity and presence of noise is evident from the comparison in Fig. 6, which shows the captured sweeps for the “relaxed” and “raised” levels, together with the corresponding magnitude frequency responses computed using Eq. (1).

Fig. 6
figure 6

Example frequency response for the measurement using DAS P9. On the left and in the middle, the spectrograms of two captured sweep signals are shown. On the right, the frequency responses of the system are shown, computed using the captured sweep signals and the associated data from APx.

Full size image

Due to the reasons mentioned above, the frequency response is perceived as unreliable in this use case. However, subjective analysis of the visualized spectrum of the sweep signal might still offer some insights, which is why the spectrograms are also presented in the experiments.

Stepped sweep sine signal

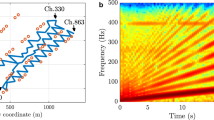
The input test signal comprises 85 consecutive time segments, each containing a single sinusoid at a specific frequency f. During the experiments, 85 target frequency values f were utilized, logarithmically distributed from 50 Hz to 6.4 kHz. The test signal measured by the microphone can be seen in Fig. 7 using the spectrogram, or in a customized spectrogram in Fig. 8. The spectrogram used for this visualization is designed so that the steps at logarithmically distributed frequencies are clearly visible. For this reason, the frequency axis is also logarithmic (which is not the case in usual spectrograms), and the frequency bins (rows of the spectrogram) are centered around the target frequencies in the test signal.

Fig. 7
figure 7

Stepped sine source signal, visualized using classical short-time Fourier transform and the magnitude spectrogram. Since the frequency steps are logarithmically spaced, it is observed that, over time, the frequency shift between adjacent steps increases. As each step contains a pure sine wave (i.e., all energy is concentrated at a single frequency), the visible horizontal lines are extremely narrow.

Full size image
Fig. 8
figure 8

Stepped sine source signal, visualized using custom spectrogam.

Full size image

The signal acquired from the fiber is analyzed by first dividing it into segments corresponding to the duration of the frequency steps of the input signal. This mapping between the time segments of the signal and the target frequencies then enables a frequency-dependent analysis of the sensing capabilities of the system.

STIPA

STIPA is a metric used to measure the intelligibility of speech transmitted through various transmission channels, such as rooms, telephone lines, or electro-acoustic systems. STI accounts for the physical characteristics of the transmission channel as well as both analog and digital processing effects to numerically summarize how well the channel preserves speech intelligibility. STI ranges from 0 to 1, see Fig. 9, with values closer to 1 indicating better intelligibility. For example, STI of 0.58 suggests a high-quality public addresses (PA) system where a native listener can understand complex messages in familiar contexts27.

Fig. 9
figure 9

The indicative STI scale as present in annexes H and I of the standard27.

Full size image

There are two methods to derive the STI: the direct method, which uses a speech-like measurement signal, and the indirect method, which uses the impulse response to compute modulation indexes from which the STI is calculated and is suitable only for linear, time-invariant systems. The direct method, preferred for its ability to handle mild nonlinear distortions and high-level noise, involves modulating a broadband pink noise with two different amplitude modulations in each of seven octave bands. This signal, when transmitted through a channel, experiences modulation depth reductions, which are quantified and processed to compute the STI. The Matlab implementation of this method involves steps such as band-filtering, envelope detection, modulation depth calculation, and adjustments for ambient noise and auditory effects, resulting in a final STI value that indicates the intelligibility quality of the speech transmission channel18.

Data Records

The dataset is available through Figshare16. The dataset contains separate files from measurements of individual test signals – background noise (background), continuous-frequency sweep (cont_freq), stepped-frequency sweep (stepped_freq) and STIPA – in the hierarchical data format version 5 (HDF5). These measurements are divided into two folders das_sp1 and das_p9. Both folders contain the measured signals for the relaxed, normal, and raised levels described in the acoustic part of the chapter. Individual files store both measurement data and DAS parameter settings (in attributes of HDF5 files), an example of parameters is shown in Table 2.

Table 2 Example of acquisition attributes from HDF5 file.
Full size table

In addition, all source signals in waveform audio file format (WAV) are attached to the dataset in folder audio. The dataset also includes recordings from the reference microphone for the background, continuous frequency sweep, and STIPA signals, and the final report produced by the APx analyzer (folder APx525). The dataset also contains Matlab scripts that are used to read the HDF5 data, and to calculate the frequency response.

Technical Validation

As part of the technical validation, the correctness of the code for calculating the STI value was verified and validated against the commercial measuring instrument NTi Audio XL2. The STI values calculated by the Matlab implementation of the STIPA direct method correspond to the values measured in the 12 verification measurements18.