Introduction

Solitary wave solutions to the nonlinear partial differential equations (NLPDEs) have been gaining attention due to their potential to provide insights into a broad spectrum of physical phenomena in a wide range of domains. Fluid dynamics, thermodynamics, hydrodynamics, optical fibres, and ocean engineering are some of engineering and scientific disciplines where nonlinear wave phenomena occur and have fundamental importance. The search for analytical and numerical solutions to NLPDEs has received a lot of attention from physicists and mathematicians. To develop the traveling wave solutions to NLPDEs, they used a variety of direct and effective methods1,2,3,4,5,6,7,8 some of them are modified simple equation method9, new extended algebraic method10, Backlund transform method11, and many others. For calculating exact solutions of the (2+1) dimensional Kundu–MukherjeeNaskar (KMN) problem12, the new extended direct algebraic method, a recently developed methodology, is adopted by the researchers. In addition, for a two-dimensional modified Zakharov–Kuznetsov equation13, numerous analytical and numerical solutions are found that had stability properties. Similarly,14,15,16,17,18 contains several more efficient strategies to consider.

Nonlinear fractional differential equations (NFDEs) play a significant role in a wide range of phenomena, including acoustic waves, hydromagnetic waves, fractal dynamics, and plenty of others, where systems display complex factors including power-law distributions, fractal patterns, and non-Markovian motion. A real order fractional derivative has undergone much development during the past few decades. Research on fractional derivative operators is often discussed in academic circles. Nonlinear fractional derivatives are used in signal processing to process and evaluate signals that have non-Gaussian characteristics and nonlinear dynamics. When attempting to extract features from complicated signals, as those seen in chaotic systems, non-stationary processes, or nonlinear dynamics, they are especially helpful. In recent years, a great deal of effort has gone into this area, and many discoveries have been made, some of which are included in19,20,21,22,23.

Granular materials are used in a diverse variety of engineering and science applications. By combining distinct solid and macroscopic particles, granular matter is formed. During their collisions, the particles interact and lose energy. The vdW equation35,36 is given by

$$\begin{aligned} \frac{\partial ^2{u}}{\partial {t}^2}+\frac{\partial ^2}{\partial {x}^2}(\frac{\partial ^2{u}}{\partial {x}^2}-\eta \frac{\partial {u}}{\partial {t}}-u^3-\varrho {u})=0, \end{aligned}$$
(1)

where u signifies the correction to critical average vertical density, x denotes the granular system’s horizontal direction, \(\eta\) is the efficient viscosity, and \(\varrho\) is the factor of bifurcation, which is corresponding to the compressibility coefficient. Accounting for the pressure surrounding the critical average vertical density are the first two terms on the left-hand side. An example of the interface tension is given by the term with a high spatial derivative.

The vdW equation for fluidized granular matter has been solved by most researchers in recent years using various methodologies24,25,26. The goal of this paper is to compare two distinct interpretations of fractional derivatives for the discovered soliton figures, in addition to discovering new families of soliton solutions for the vdW equation by using extended direct algebraic methods. This type of analysis has never been done before for the model in question, therefore it’s worth mentioning here.

The paper’s layout is seen here: Sect. “Basic definitions” contains some fundamental definitions collected from the literature. The examination of the governing model using various definitions is described in Sect. “Governing equation”. The extended direct algebraic method’s general technique and its implementation are presented in Sect. “Soliton solutions”. In Sect. “Study of solutions with various fractional derivatives in comparison, a thorough comparison” study is carried out. The conclusion is provided at the end of the article.

Basic definitions

Beta derivative

Definition 2.1

The following is the definition of beta derivative19:

$$\begin{aligned} _{0}^{A}T^{\alpha }_{x}(G(x))=\lim _{\varepsilon \rightarrow \infty }\frac{G(x+\varepsilon (x+\frac{1}{\Gamma (\alpha )}))-G(x)}{\varepsilon }, \end{aligned}$$
(2)

with these properties.

Theorem 2.2

If \(0<\alpha <1\), \(a,b\in R,F,C\) and differentiable of \(\alpha\) order at a \(point>0\), then:

  1. 1.

    \(_{0}^{A}T^{\alpha }_{x}(aF(x)+bG(x))=a_{0}^AT^{\alpha }_{x}F(x)+b_{0}^AT^{\alpha }_{x}G(x)\);

  2. 2.

    \(_{0}^AT^{\alpha }_{x}(k)=0\), where k represent the constant term.

  3. 3.

    \(_{0}^{A}T^{\alpha }_{x}(F(x)*G(x))=G(x)_{0}^AT^{\alpha }_{x}F(x)+F(x)_{0}^AT^{\alpha }_{x}G(x)\);

  4. 4.

    \(_{0}^{A}T^{\alpha }_{x}(\frac{F(x)}{G(x)})=\frac{G(x)_{0}^AT^{\alpha }_{x}F(x)-F(x)_{0}^AT^{\alpha }_{x}G(x)}{G^2(x)}\);

  5. 5.

    \(_{0}^{A}T^{\alpha }_{x}(\frac{F(t)}{G(x)})=tF'(t)\).

The proof of given relations are mentioned in27

M-truncated derivative

Definition 2.3

The one-parameter shortened Mittag-Leffler function20 is described as given:

$$\begin{aligned} \iota E_{\beta }(z)=\sum \limits _{k=1}^\iota (\frac{z^k}{\Gamma (k\beta +1)}, \end{aligned}$$
(3)

in which \(\beta >0\) and \(z\in C\).

Definition 2.4

Assume that \(g:[0, \infty )\rightarrow R\) and \(\alpha \in (0,1)\), The definition of the M-truncated derivatives of g with degree \(\alpha\) is:

$$\begin{aligned} \iota T^{\alpha ,\beta }_{M}g(t)=\lim _{\varepsilon \rightarrow \infty }\frac{g(t+E_{\beta }(\varepsilon t^{-\alpha }))-g(t)}{\varepsilon }, \end{aligned}$$
(4)

for \(t>0\) and \(E_{\beta }(.)\), \(\beta >0\).

Theorem 2.5

If \(\alpha \in (0,1]\), \(\beta >0\), g and h are differentiable upto \(\alpha\) order for \(t>0\), we have:

  1. 1.

    \(\iota T^{\alpha ,\beta }_{M}(pg+qh)=p\iota T^{\alpha ,\beta }{M}(g)+q\iota T^{\alpha ,\beta }_{M}(h)\);

  2. 2.

    \(\iota T^{\alpha ,\beta }_{M}(t^v)=vt^{v-\alpha }, v\in R\);

  3. 3.

    \(\iota T^{\alpha ,\beta }_{M}(gh)=g\iota T^{\alpha ,\beta }_{M}(h)+h\iota T^{\alpha ,\beta }_{M}(g)\);

  4. 4.

    \(\iota T^{\alpha ,\beta }_{M}(\frac{g}{h})=\frac{g\iota T^{\alpha ,\beta }_{M}(h)-h\iota T^{\alpha ,\beta }_{M}(g)}{h^2}\);

  5. 5.

    \(\iota T^{\alpha ,\beta }_{M}(g(t)=\frac{t^{1-\alpha }}{\Gamma (\beta +1)}g'(t)\);

  6. 6.

    \(\iota T^{\alpha ,\beta }_{M}(g.h)=f'(h(t))\iota T^{\alpha ,\beta }_{M}h(t)\).

Governing equation

The vdW equation is presented in this section with respect to several types of derivatives.

  1. (i)

    The discussed equation can be stated as follows when the beta derivative is considered:

    $$\begin{aligned} _{0}^{A}D^{2\alpha }_{t}u+_{0}^{A}D^{2\alpha }_{x}(_{0}^{A}D^{2\alpha }_{x}u-\eta _{0}^{A}D^{\alpha }_{t}u-u^3-\varrho u)=0, \end{aligned}$$
    (5)

    where \(_{0}^{A}D^{\alpha }_{t}\) and \(_{0}^{A}D^{\alpha }_{x}\) represent beta derivatives of t and x respectively.

  2. (ii)

    When using the M-truncated derivative formulation, the equation becomes:

    $$\begin{aligned} _{0}^{A}D^{2\alpha ,\beta }_{M,t}u+_{0}^{A}D^{2\alpha ,\beta }_{M,x}(_{0}^{A}D^{2\alpha ,\beta }_{M,x}u-\eta _{0}^{A}D^{\alpha ,\beta }_{M,t}u-u^3-\varrho u)=0, \end{aligned}$$
    (6)

    where \(_{0}^{A}D^{\alpha ,\beta }_{M,t}\) and \(_{0}^{A}D^{\alpha ,\beta }_{M,x}\) are M-truncated derivatives of t and x respectively.

Mathematical analysis

We’ll use the following transformation to solve Eqs. (5) and (6):

$$\begin{aligned} u(x,t)=U(\tau ), \end{aligned}$$
(7)

where the soliton’s pulse shape is indicated by u(x, t) and \(\tau\) is defined in various ways: In the case of the beta derivative, \(\tau\) is calculated as

$$\begin{aligned} \tau =\frac{j}{\alpha }(x+\frac{1}{\Gamma (\alpha )})^{\alpha }-\frac{w}{\alpha }(t+\frac{1}{\Gamma (\alpha )})^{\alpha }, \end{aligned}$$
(8)

Whereas, in the sense of an M-truncated derivative, we have

$$\begin{aligned} \tau =\frac{\Gamma (\beta +1)}{\alpha }(jx^{\alpha }-wt^{\alpha }), \end{aligned}$$
(9)

where j and w stand for the wave number and speed of solitons. By using the transformation (7) in Eqs. (5) and (6), we obtain the ordinary differential equation as follows:

$$\begin{aligned} \frac{w^2-\varrho j^2}{j^2}U+j^2U''+\eta wU'-U^3=0, \end{aligned}$$
(10)

Soliton solutions

In this section, we find solitons solutions for the vdW problem with beta and M-truncated derivative using an expanded direct algebraic approach.

Method description

The description of the new expanded direct algebraic approach28,29,30,31,32,33,34 is explained in this part. This technique can be used to solve several additional non-linear partial differential equations that arise in scientific research and is more efficient and useful to find several solitary wave solutions for a variety of non-linear issues. The researchers claim that the new extended algebraic approach gives a more powerful mathematical framework for non-linear partial differential equations than any other strategy. This is done with the aid of symbolic calculation. Suppose the non-linear partial differential equation is in the form:

$$\begin{aligned} r(z,z_{t},z_{x},z_{tt},z_{xx},...)=0, \end{aligned}$$
(11)

By \(u(x,t)=U(\tau )\), we obtain:

$$\begin{aligned} R(Z,Z^{'},Z^{''},...)=0. \end{aligned}$$
(12)

Suppose that:

$$\begin{aligned} U(\tau )=a_{0}+\sum _{i=1}^{N} \bigg [a_{i}Z(\tau )^{i-1}\bigg ], \end{aligned}$$
(13)

where

$$\begin{aligned} Z'(\tau )=ln(\rho )\left( \nu +\kappa Z(\tau ) + \lambda Z^2 (\tau )\right) . \end{aligned}$$
(14)

We have

\(\mu _{1}=(\beta ^2-4\alpha \gamma )\).

  1. (1)

    For \(\mu _{1} < 0\) and \(\gamma \ne 0,\)

    $$\begin{aligned} Z_{1}(\tau )= & {} -\frac{\kappa }{2\lambda }+\frac{\sqrt{-\mu _{1}}}{2\lambda }\tan _{\rho }\left( \frac{\sqrt{-\mu _{1}}}{2}\tau \right) , \\ Z_{2}(\tau )= & {} -\frac{\kappa }{2\lambda }-\frac{\sqrt{-\mu _{1}}}{2\lambda }\cot _{\rho }\left( \frac{\sqrt{-\mu _{1}}}{2}\tau \right) , \\ Z_{3}(\tau )= & {} -\frac{\kappa }{2\lambda }+\frac{\sqrt{-\mu _{1}}}{2\lambda }\left( \tan _{\rho }\left( \sqrt{-\left( \mu _{1}\right) }\tau \right) \pm \sqrt{pq}\sec _{\rho }\left( \sqrt{-\left( \mu _{1}\right) }\tau \right) \right) , \\ Z_{4}(\tau )= & {} -\frac{\kappa }{2\lambda }+\frac{\sqrt{-\mu _{1}}}{2\lambda }\left( \cot _{\rho }\left( \sqrt{-\left( \mu _{1}\right) }\tau \right) \pm \sqrt{pq}\csc _{\rho }\left( \sqrt{-\left( \mu _{1}\right) }\tau \right) \right) , \\ Z_{5}(\tau )= & {} -\frac{\kappa }{2\lambda }+\frac{\sqrt{-\mu _{1}}}{4\lambda }\left( \tan _{\rho }\left( \frac{\sqrt{-\mu _{1}}}{4}\tau \right) -\cot _{\rho }\left( \frac{\sqrt{-\mu _{1}}}{4}\tau \right) \right) . \end{aligned}$$
  2. (2)

    For \(\mu _{1} > 0\) and \(\gamma \ne 0,\)

    $$\begin{aligned} Z_{6}(\tau )= & {} -\frac{\kappa }{2\lambda }-\frac{\sqrt{\mu _{1}}}{2\lambda }\tanh _{\rho }\left( \frac{\sqrt{\mu _{1}}}{2}\xi \right) , \\ Z_{7}(\tau )= & {} -\frac{\kappa }{2\lambda }-\frac{\sqrt{\mu _{1}}}{2\lambda }\coth _{\rho }\left( \frac{\sqrt{\mu _{1}}}{2}\xi \right) , \\ Z_{8}(\tau )= & {} -\frac{\kappa }{2\lambda }+\frac{\sqrt{\mu _{1}}}{2\lambda }\left( -\tanh _{\rho }\left( \sqrt{\left( \mu _{1}\right) }\tau \right) \pm \iota \sqrt{pq}{{\,\textrm{sech}\,}}_{\rho }\left( \sqrt{\left( \mu _{1}\right) }\tau \right) \right) , \\ Z_{9}(\tau )= & {} -\frac{\kappa }{2\lambda }+\frac{\sqrt{\mu _{1}}}{2\lambda }\left( -\coth _{\rho }\left( \sqrt{\left( \mu _{1}\right) }\tau \right) \pm \sqrt{pq}{{\,\textrm{csch}\,}}_{\rho }\left( \sqrt{\left( \mu _{1}\right) }\tau \right) \right) , \\ Z_{10}(\tau )= & {} -\frac{\kappa }{2\lambda }-\frac{\sqrt{\mu _{1}}}{4\lambda }\left( \tanh _{\rho }\left( \frac{\sqrt{\mu _{1}}}{4}\tau \right) +\coth _{\rho }\left( \frac{\sqrt{\mu _{1}}}{4}\tau \right) \right) . \end{aligned}$$
  3. (3)

    For \(\alpha \gamma > 0\) and \(\beta =0,\)

    $$\begin{aligned} Z_{11}(\tau )= & {} \sqrt{\frac{\nu }{\lambda }}\tan _{\rho }\left( \sqrt{\nu \lambda }\tau \right) , \\ Z_{12}(\tau )= & {} -\sqrt{\frac{\nu }{\lambda }}\cot _{\rho }\left( \sqrt{\nu \lambda }\tau \right) , \\ Z_{13}(\tau )= & {} \sqrt{\frac{\nu }{\lambda }}\left( \tan _{\rho }\left( 2\sqrt{\left( \nu \lambda \right) }\tau \right) \pm \sqrt{pq}\sec _{\rho }\left( 2\sqrt{\left( \nu \lambda \right) }\tau \right) \right) , \\ Z_{14}(\tau )= & {} \sqrt{\frac{\nu }{\lambda }}\left( -\cot _{\rho }\left( 2\sqrt{\left( \nu \lambda \right) }\tau \right) \pm \sqrt{pq}\csc _{\rho }\left( 2\sqrt{\left( \nu \lambda \right) }\tau \right) \right) , \\ Z_{15}(\tau )= & {} \frac{1}{2}\sqrt{\frac{\nu }{\lambda }}\left( \tan _{\rho }\left( \frac{\sqrt{\nu \lambda }}{2}\xi \right) -\cot _{\kappa }\left( \frac{\sqrt{(\nu \gamma )}}{2}\xi \right) \right) . \end{aligned}$$
  4. (4)

    When \(\alpha \gamma < 0\) and \(\beta =0,\)

    $$\begin{aligned} Z_{16}(\tau )= & {} -\sqrt{-\frac{\nu }{\lambda }}\tanh _{\rho }\left( \sqrt{-\left( \nu \lambda \right) }\tau \right) , \\ Z_{17}(\tau )= & {} -\sqrt{-\frac{\nu }{\lambda }}\coth _{\rho }\left( \sqrt{-\left( \nu \lambda \right) }\tau \right) , \\ Z_{18}(\tau )= & {} \sqrt{-\frac{\nu }{\lambda }}\left( -\tanh _{\rho }\left( 2\sqrt{-\left( \nu \lambda \right) }\tau \right) \pm i\sqrt{pq}{{\,\textrm{sech}\,}}_{\rho }\left( 2\sqrt{-\left( \nu \lambda \right) }\tau \right) \right) , \\ Z_{19}(\tau )= & {} \sqrt{-\frac{\nu }{\lambda }}\left( -\coth _{\rho }\left( 2\sqrt{-\left( \nu \lambda \right) }\tau \right) \pm \sqrt{pq}{{\,\textrm{csch}\,}}_{\rho }\left( 2\sqrt{-\left( \nu \lambda \right) }\tau \right) \right) , \\ Z_{20}(\tau )= & {} -\frac{1}{2}\sqrt{-\frac{\nu }{\lambda }}\left( \tanh _{\rho }\left( \frac{\sqrt{-\nu \lambda }}{2}\tau \right) +\coth _{\rho }\left( \frac{\sqrt{-\nu \lambda }}{2}\tau \right) \right) . \end{aligned}$$

    (5) For \(\beta = 0\) and \(\alpha =\gamma ,\)

    $$\begin{aligned} Z_{21}(\tau )= & {} \tan _{\rho }\left( \nu \tau \right) , \\ Z_{22}(\tau )= & {} -\cot _{\rho }\left( \nu \tau \right) , \\ Z_{23}(\tau )= & {} \tan _{\rho }\left( 2\nu \tau \right) \pm \sqrt{pq}\sec _{\rho }\left( 2\nu \tau \right) , \\ Z_{24}(\tau )= & {} -\cot _{\rho }\left( 2\nu \tau \right) \pm \sqrt{pq}\csc _{\rho }\left( 2\nu \tau \right) , \\ Z_{25}(\tau )= & {} \frac{1}{2}\left( \tan _{\rho }\left( \frac{\nu }{2}\tau \right) -\cot _{\rho }\left( \frac{\nu }{2}\tau \right) \right) . \end{aligned}$$
  5. (5)

    For \(\beta = 0\) and \(\gamma =-\alpha ,\)

    $$\begin{aligned} Z_{26}(\tau )= & {} -\tanh _{\rho }\left( \nu \tau \right) , \\ Z_{27}(\tau )= & {} -\coth _{\rho }\left( \nu \tau \right) , \\ Z_{28}(\tau )= & {} -\tanh _{\rho }\left( 2\nu \tau \right) \pm i \sqrt{pq}{{\,\textrm{sech}\,}}_{\rho }\left( 2\nu \tau \right) , \\ Z_{29}(\tau )= & {} -\coth _{\rho }\left( 2\nu \tau \right) \pm \sqrt{pq}{{\,\textrm{csch}\,}}_{\rho }\left( 2\nu \tau \right) , \\ Z_{30}(\tau )= & {} -\frac{1}{2}\bigg (\tanh _{\rho }\left( \frac{\nu }{2}\tau \right) +\coth _{\rho }\left( \frac{\nu }{2}\tau \right) \bigg ). \end{aligned}$$
  6. (6)

    For \(\beta ^2 = 4\alpha \gamma\),

    $$\begin{aligned} Z_{31}(\tau )= & {} \frac{-2\nu (\kappa \tau \ln \rho +2)}{\kappa ^2\tau \ln \rho }. \end{aligned}$$
  7. (7)

    When \(\beta = e,\alpha = ef, (f\ne 0)\) and \(\gamma =0\),

    $$\begin{aligned} Z_{32}(\tau )= & {} \rho ^{e\tau } -f. \end{aligned}$$
  8. (8)

    When \(\beta = \gamma = 0\),

    $$\begin{aligned} Z_{33}(\tau )=\nu \tau \ln \rho . \end{aligned}$$
  9. (9)

    For \(\beta = \alpha = 0\),

    $$\begin{aligned} Z_{34}(\tau )=\frac{-1}{\lambda \tau \ln \rho }. \end{aligned}$$
  10. (10)

    For \(\alpha = 0\) and \(\beta \ne 0\),

    $$\begin{aligned} Z_{35}(\tau )= & {} -\frac{p\kappa }{\lambda \left( \cosh _{\rho }\left( \kappa \tau \right) -\sinh _{\rho }\left( \kappa \tau \right) + p\right) }. \\ Z_{36}(\tau )= & {} -\frac{\kappa \left( \sinh _{\rho }\left( \kappa \tau \right) +\cosh _{\rho }\left( \kappa \tau \right) \right) }{\lambda \left( \sinh _{\rho }\left( \kappa \tau \right) +\cosh _{\rho }\left( \kappa \tau \right) + q\right) }. \end{aligned}$$
  11. (11)

    For \(\beta = e, \gamma =ef,~(f\ne 0\) and \(\alpha =0)\),

    $$\begin{aligned} Z_{37}(\tau )= & {} -\frac{p\rho ^{e\tau }}{p-fq\rho ^{e\tau }}. \\ \sinh _{\rho }(\tau )= & {} \frac{m\rho ^\tau -q\rho ^{-\tau }}{2},~ \cosh _{\kappa }(\xi )=\frac{p\rho ^\tau +n\rho ^{-\tau }}{2}. \\ \tanh _{\rho }(\tau )= & {} \frac{p\rho ^\tau -q\rho ^{-\tau }}{p\rho ^\tau +n\rho ^{-\tau }}, ~ \coth _{\rho }(\tau )=\frac{p\rho ^\tau +q\rho ^{-\tau }}{p\rho ^\tau -q\rho ^{-\tau }}. \\ {{\,\textrm{sech}\,}}_{\rho }(\tau )= & {} \frac{2}{p\rho ^\tau +q\rho ^{-\tau }},~{{\,\textrm{csch}\,}}_{\rho }(\tau )=\frac{2}{p\rho ^\tau -n\rho ^{-\tau }}. \\ \sin _{\rho }(\tau )= & {} \frac{p\rho ^{i\tau }-q\rho ^{-i\tau }}{2i},~ \cos _{\rho }(\tau )=\frac{p\rho ^{i\tau }+q\rho ^{-i\tau }}{2}. \\ \tan _{\rho }(\tau )= & {} -i\frac{p\rho ^{i\tau }-q\rho ^{-i\tau }}{p\rho ^{i\tau }+q\rho ^{-i\tau }}, ~~\cot _{\rho }(\tau )=i\frac{p\rho ^{i\tau }+q\rho ^{-i\tau }}{p\rho ^{i\tau }-q\rho ^{-i\tau }}. \\ \sec _{\rho }(\tau )= & {} \frac{2}{p\rho ^\tau +q\rho ^{-\tau }},~~\csc _{\rho }(\tau )=\frac{2i}{p\rho ^\tau -q\rho ^{-\tau }}. \end{aligned}$$

Implimentation of the method

The purpose of the given section is to identify the solitary solutions for the provided framework, including various derivatives. To do so, first solve Eq. (12). After balancing the highest-order derivative terms with the nonlinear terms in Eq. (12), we will get N = 1. So the solution will be of the following kind:

$$\begin{aligned} U(\tau )=a_{0}+a_{1}Z(\tau ), \end{aligned}$$
(15)

where \(Z(\tau )\) satisfies \(Z'(\tau )=ln(p)\left( \gamma +k Z(\tau ) + r Z^2 (\tau )\right)\). Then, we obtain \(~~~~~~~~Z^{0}(\tau )\)  : \(-a_{0}\varrho +\frac{a_{0}w^2}{j^2}+j^2a_{1}k\ln (p)^2\gamma +w\eta \gamma a_{1}\ln (p)-a_{0}^3=0\), \(~~~~~~~~Z^{1}(\tau )\)  : \(-a_{1}\varrho +\frac{a_{1}w^2}{j^2}+j^2a_{1}k^2\ln (p)^2+2j^2a_{1}r\gamma \ln (p)^2+a_{1}kw\eta \ln (p)-3a_{0}^2a_{1}=0\), \(~~~~~~~~Z^{2}(\tau )\)  : \(3j^2a_{1}kr\ln (p)^2+rwa_{1}\eta \ln (p)-3a_{0}a_{1}^2=0\), \(~~~~~~~~Z^{3}(\tau )\)  : \(2j^2a_{1}r^2\ln (p)^2-a_{1}^3=0\). Thus, we obtain

       \(a_{0}=\sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}\), \(~~a_{1} =\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c}\), \(~~w=\frac{3k\eta ^3\varrho ^2(k^2-4r\gamma }{b\ln {p}}\), \(~~j=\frac{\eta \sqrt{\varrho }}{-c\ln {p}^2}\), where

$$\begin{aligned} b=\sqrt{k^2\eta ^4(9-2\eta ^2)^2\varrho ^2(k^2-4r\gamma )^3}, \\ c=(-9+2\eta ^2)(k^2-4r\gamma ). \end{aligned}$$

Let \(l=k^2-4r\gamma\). Now, we will discuss all the cases for the proposed method: Case 1. If \(l < 0\) and \(r\ne 0,\) then:

$$\begin{aligned} U_{1}= & {} \sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c}\left( -\frac{k}{2r}+\frac{\sqrt{-l}}{2r}tan_{p}\left[ \frac{\sqrt{-l}}{2}\tau \right] \right) , \end{aligned}$$
(16)
$$\begin{aligned} U_{2}= & {} \sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c}\left( -\frac{k}{2r}-\frac{\sqrt{-l}}{2r}cot_{p}\left[ \frac{\sqrt{-l}}{2}\tau \right] \right) , \end{aligned}$$
(17)
$$\begin{aligned} U_{3}= & {} \sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c}\left( -\frac{k}{2r}+\frac{\sqrt{-l}}{2r}\left( tan_{p}\left( \sqrt{-l}\tau \right) \pm \sqrt{gh}.sec_{p}\left( \sqrt{-l}\tau \right) \right) \right) , \end{aligned}$$
(18)
$$\begin{aligned} U_{4}= & {} \sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c}\left( -\frac{k}{2r}+\frac{\sqrt{-l}}{2r}\left( -cot_{p}\left( \sqrt{-l}\tau \right) \pm \sqrt{gh}.csc_{p}\left( \sqrt{-l}\tau \right) \right) \right) , \end{aligned}$$
(19)
$$\begin{aligned} U_{5}= & {} \sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c}\left( -\frac{k}{2r}+\frac{\sqrt{-l}}{4r}\left( tan_{p}\left( \frac{\sqrt{-l}}{4}\tau \right) -cot_{p}\left( \frac{\sqrt{-l}}{4}\tau \right) \right) \right) . \end{aligned}$$
(20)

Case 2. If \(l > 0\) and \(r\ne 0\), then:

$$\begin{aligned} U_{6}= & {} \sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c}\left( -\frac{k}{2r}-\frac{\sqrt{l}}{2r}tanh_{p}\left[ \frac{\sqrt{l}}{2}\tau \right] \right) , \end{aligned}$$
(21)
$$\begin{aligned} U_{7}= & {} \sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c}\left( -\frac{k}{2r}-\frac{\sqrt{l}}{2r}coth_{p}\left[ \frac{\sqrt{l}}{2}\tau \right] \right) , \end{aligned}$$
(22)
$$\begin{aligned} U_{8}= & {} \sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c}\left( -\frac{k}{2r}+\frac{\sqrt{l}}{2r}\left( -tanh_{p}\left( \sqrt{l}\tau \right) \pm \iota \sqrt{gh}.sech_{p}\left( \sqrt{l}\tau \right) \right) \right) , \end{aligned}$$
(23)
$$\begin{aligned} U_{9}= & {} \sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c}\left( -\frac{k}{2r}+\frac{\sqrt{l}}{2r}\left( -coth_{p}\left( \sqrt{l}\tau \right) \pm \sqrt{gh}.csch_{p}\left( \sqrt{l}\tau \right) \right) \right) , \end{aligned}$$
(24)
$$\begin{aligned} U_{10}= & {} \sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2 k\eta ^{2}\varrho c}\left( -\frac{k}{2r}+\frac{\sqrt{l}}{4r}\left( tanh_{p}\left( \frac{\sqrt{l}}{4}\tau \right) +coth_{p}\left( \frac{\sqrt{l}}{4}\tau \right) \right) \right) . \end{aligned}$$
(25)

Case 3. If \(\gamma .r>0\) and \(k=0\), then :

$$\begin{aligned} U_{11}= & {} \sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c}\left( \sqrt{\frac{\gamma }{r}}\left( tan_{p}\left( \sqrt{\gamma . r}\tau \right) \right) \right) , \end{aligned}$$
(26)
$$\begin{aligned} U_{12}= & {} \sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c}\left( -\sqrt{\frac{\gamma }{r}}\left( cot_{p}\left( \sqrt{\gamma . r}\tau \right) \right) \right) , \end{aligned}$$
(27)
$$\begin{aligned} U_{13}= & {} \sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c}\left( \sqrt{\frac{\gamma }{r}}\left( tan_{p}\left( 2\sqrt{\gamma . r}\tau \right) \pm \sqrt{gh}.sec_{p}\left( 2\sqrt{\gamma .r}\tau \right) \right) \right) , \end{aligned}$$
(28)
$$\begin{aligned} U_{14}= & {} \sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c}\left( \sqrt{\frac{\gamma }{r}}\left( -cot_{p}\left( 2\sqrt{\gamma . r}\tau \right) \pm \sqrt{gh}.csc_{p}\left( 2\sqrt{\gamma .r}\tau \right) \right) \right) , \end{aligned}$$
(29)
$$\begin{aligned} U_{15}= & {} \sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c}\left( \frac{1}{2}\sqrt{\frac{\gamma }{r}}\left( tan_{p}\left( \frac{\sqrt{\gamma . r}}{2}\tau \right) -cot_{p}\left( \frac{\sqrt{\gamma .r}}{2}\tau \right) \right) \right) . \end{aligned}$$
(30)

Case 4. If \(\gamma .r< 0\) and \(k=0,\) then:

$$\begin{aligned} U_{16}= & {} \sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c}\left( -\sqrt{-\frac{\gamma }{r}}\left( tanh_{p}\left( \sqrt{-\gamma . r}\tau \right) \right) \right) , \end{aligned}$$
(31)
$$\begin{aligned} U_{17}= & {} \sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c}\left( -\sqrt{-\frac{\gamma }{r}}\left( coth_{p}\left( \sqrt{-\gamma . r}\tau \right) \right) \right) , \end{aligned}$$
(32)
$$\begin{aligned} U_{18}= & {} \sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c}\left( \sqrt{-\frac{\gamma }{r}}\left( -tanh_{p}\left( 2\sqrt{-\gamma . r}\tau \right) \pm \iota \sqrt{gh}.sech_{p}\left( 2\sqrt{-\gamma .r}\tau \right) \right) \right) , \end{aligned}$$
(33)
$$\begin{aligned} U_{19}= & {} \sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c}\left( \sqrt{-\frac{\gamma }{r}}\left( -coth_{p}\left( 2\sqrt{-\gamma . r}\tau \right) \pm \iota \sqrt{gh}.csch_{p}\left( 2\sqrt{-\gamma .r}\tau \right) \right) \right) , \end{aligned}$$
(34)
$$\begin{aligned} U_{20}= & {} \sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c}\left( -\frac{1}{2}\sqrt{-\frac{\gamma }{r}}\left( tanh_{p}\left( \frac{\sqrt{-\gamma . r}}{2}\tau \right) +cot_{p}\left( \frac{\sqrt{-\gamma .r}}{2}\tau \right) \right) \right) . \end{aligned}$$
(35)

Case 5. If \(k = 0\) and \(\gamma =r,\) then:

$$\begin{aligned} U_{21}= & {} sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c }tan_{p}(\gamma \tau ), \end{aligned}$$
(36)
$$\begin{aligned} U_{22}= & {} sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c }(-cot_{p}(\gamma \tau )), \end{aligned}$$
(37)
$$\begin{aligned} U_{23}= & {} sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c }(tan_{p}(2\gamma \tau )\pm \sqrt{gh}.sec_{p}(2\gamma .\tau )), \end{aligned}$$
(38)
$$\begin{aligned} U_{24}= & {} sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c }(-cot_{p}(2\gamma \tau )\pm \sqrt{gh}.csc_{p}(2\gamma .\tau )) \end{aligned}$$
(39)
$$\begin{aligned} U_{25}= & {} \sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c}\left( \frac{1}{2})\left( tan_{p}\left( \frac{\gamma }{2}\tau \right) -cot_{p}\left( \frac{\gamma }{2}\tau \right) \right) \right) . \end{aligned}$$
(40)

Case 6. If \(= 0\) and \(r=-\gamma ,\) then:

$$\begin{aligned}{} & {} U_{26}sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c }(-tanh_{p}(\gamma \tau )), \end{aligned}$$
(41)
$$\begin{aligned}{} & {} \quad U_{27}sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c }(-coth_{p}(\gamma \tau )), \end{aligned}$$
(42)
$$\begin{aligned}{} & {} \quad U_{28}=sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c }(-tanh_{p}(2\gamma \tau )\pm \iota \sqrt{gh}.sech_{p}(2\gamma .\tau )), \end{aligned}$$
(43)
$$\begin{aligned}{} & {} \quad U_{29}=sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c }(-coth_{p}(2\gamma \tau )\pm \sqrt{gh}.csch_{p}(2\gamma .\tau )), \end{aligned}$$
(44)
$$\begin{aligned}{} & {} \quad U_{30}=\sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c}\left( -\frac{1}{2})\left( tanh_{p}\left( \frac{\gamma }{2}\tau \right) +coth_{p}\left( \frac{\gamma }{2}\tau \right) \right) \right) . \end{aligned}$$
(45)

(7): For \(k^2 = 4\gamma r\), then:

$$\begin{aligned} U_{31}=\sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c}\left( \frac{-2\gamma (k\tau \ln (p)+2)}{k^2\tau \ln (p)}\right) . \end{aligned}$$
(46)

(8): For \(k= d,\gamma = Nd, (N\ne 0)\) and \(r=0\), then:

$$\begin{aligned} U_{32}=\sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c}\left( p^{d\tau }-N\right) . \end{aligned}$$
(47)

(9): For \(k=r= 0\), then:

$$\begin{aligned} U_{33}=\sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c}\left( \gamma \tau \ln (p)\right) . \end{aligned}$$
(48)

(10): For \(= \gamma = 0\), then:

$$\begin{aligned} U_{34}=\sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c}\left( \frac{-1}{\tau \ln (p)r}\right) . \end{aligned}$$
(49)

(11): For \(\gamma = 0\) and \(k \ne 0\), then:

$$\begin{aligned} U_{35}= & {} \sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c}\left( \frac{gk}{\cosh _{p}\left( k\tau \right) -\sinh _{p}\left( k\tau \right) +g}\right) . \end{aligned}$$
(50)
$$\begin{aligned} U_{36}= & {} \sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c}\left( \frac{k\left( \sinh _{p}\left( k\tau \right) +\cosh _{p}\left( k\tau \right) \right) }{\sinh _{p}\left( k\tau \right) +\cosh _{p}\left( k\tau \right) +h}\right) . \end{aligned}$$
(51)

(12): For \(k = d, r=Nd,~(N\ne 0\) and \(\gamma =0)\), then:

$$\begin{aligned} U_{37}=\sqrt{\frac{b-\eta ^{2}\varrho c(k^{2}-2r\gamma )}{(9-2\eta ^2)^2 (k^2-4r\gamma )^2}}-\frac{k^{2}\eta ^{2}\varrho c+ba_{0}}{2k\eta ^{2}\varrho c}(\frac{g.p^{d.\tau }}{h-Ngp^{d.\tau }}). \end{aligned}$$
(52)

where \(g,h,d>0\) are arbitrary constant.

Study of solutions with various fractional derivatives in comparison

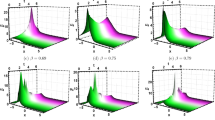
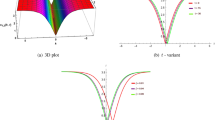
For different values of the fractional parameter \(\alpha\), two solutions, \(U_{2}\) and \(U_{6}\), are considered in this section in terms of two derivatives and shown in Figs. 1, 2,3, 4, 5, 6, 7, 8, 9 and 10. For \(U_{2}\) space, we used the parameters as \(\varrho =1, p=e, \eta =1, k=-1, \gamma =1, r=-0.5\), \(\beta =1\), and \(\alpha =0.3\). In Figure 1 a depicts the graph of the \(U_{2}\) space with the \(\beta\)-derivative, whereas b illustrates the behavior of the \(U_{2}\) space with the M-truncated derivative, and c represents a 2D depiction of both \(\beta\) and M-truncated derivatives of \(U_{2}\) at \(t=1\). In Fig. 2a exhibits its graph with the \(\beta\)-derivative with \(\alpha =0.5\), b shows its behavior using the M-truncated derivative with \(\alpha =0.5\), and c displays a 2D graph of \(U_{2}\) at \(t=1\). In Fig.  3, with \(\alpha =0.7\), a presents its graph with the \(\beta\)- derivative, b displays its behavior with an M-truncated derivative at \(\beta =1\), c offers a 2D depiction of \(U_{2}\) with both fractional derivatives at t=1. In Fig. 4a provides its graph with the beta derivative at \(\alpha =0.9\), b illustrates its behavior with the M-truncated derivative at \(\beta =1\), and c represents a 2D graph of \(U_{2}\) at time \(t=1\). In Fig. 5a displays its graph with the \(\beta\)-derivative for various values of “\(\alpha\)”, whereas b displays its behavior with the M-truncated derivative. Figure 6 displays its graph together with the \(\beta\)-derivative and an M-truncated for \(\alpha =1\) and \(\beta =0\).

Figure 1
figure 1

(a) 3D depiction of \(\beta\)- derivative with \(\alpha =0.3\) for \(U_{2}\), (b) 3D depiction of M-truncated with \(\alpha = 0.3\) for \(U_{2}\), (c) \(U_{2}\) plot in 2D for both derivatives with \(t = 1\).

Full size image
Figure 2
figure 2

(a) 3D depiction of \(U_{2}\) for \(\beta\)- derivative with \(\alpha =0.5\), (b) 3D depiction of M-truncated derivative with \(\alpha = 0.5\) for \(U_{2}\), (c) \(U_{2}\) plot in 2D with \(t = 1\).

Full size image
Figure 3
figure 3

(a) 3D depiction of \(U_{2}\) for \(\beta\)-derivative with \(\alpha =0.7\) , (b) 3D depiction of M-truncated derivative with \(\alpha = 0.7\) for \(U_{2}\), (c) \(U_{2}\) depiction in 2D for both derivatives with \(t = 1\).

Full size image
Figure 4
figure 4

(a) 3D depiction of \(U_{2}\) for \(\beta\)-derivative with \(\alpha =0.9\), (b) 3D depiction of M-truncated derivative with \(\alpha =0.9\) for \(U_{2}\), (c) \(U_{2}\) plot in 2D with \(t = 1\).

Full size image
Figure 5
figure 5

2D-depiction of \(U_{2}\) for given derivatives at \(t=1\) for multiple values of \(\alpha\).

Full size image
Figure 6
figure 6

2D-representation of \(U_{2}\) with \(\alpha =1\) and \(\beta =0\) for different derivatives.

Full size image

We have used the parameters \(\eta =1, p=e, r=1, k=-0.01, \varrho =1/6, \gamma =0.02\), and \(\beta =2\) in the equation \(U_{6}\). In Fig. 7a provides the graph of \(U_{6}\) with the beta derivative for \(\alpha =0.3\), whereas b illustrates its behavior with the M-truncated derivative with \(\alpha =0.3\) and c represents \(U_{6}\) at \(t=1\). In Fig. 8a exhibits its graph with the beta derivative with \(\alpha =0.5\), b illustrates its behavior with the M-truncated derivative with \(\beta =2\), and c represents a 2D graph of \(U_{6}\) at \(t=1\). In Fig. 9a exhibits its graph with \(\alpha =0.7\), b demonstrates its behavior with \(\beta =1\) M-truncated derivative, and c represents a 2D graph of \(U_{6}\) at \(t=1\). In Fig.  10a provides its graph with a beta derivative with \(\alpha =0.9\), b illustrates its behavior with an M-truncated derivative with \(\beta =1\), and c represents a 2D graph of \(U_{6}\) at time \(t=1\). In Fig. 11a depicts its graph with the beta derivative for various values of \(\alpha\), whereas b displays its behavior with the M-truncated derivative. Fig. 12 displays its graph together with the beta derivative and an M-truncated for \(\alpha =1\) and \(\beta =0\).

Figure 7
figure 7

(a) 3D depiction of \(U_{6}\) with \(\beta\)-derivative for \(\alpha =0.3\), (b) 3D depiction for M-truncated derivative with \(\alpha = 0.3\) for \(U_{6}\), (c) \(U_{6}\) plot in 2D for two provided derivatives with \(t = 1\).

Full size image
Figure 8
figure 8

(a) 3D depiction of \(U_{6}\) with \(\beta\)-derivative for \(\alpha =0.5\), (b) 3D representation of M-truncated derivative with \(\alpha = 0.5\) for \(U_{2}\), (c) \(U_{2}\) plot in 2D with \(t = 1\).

Full size image
Figure 9
figure 9

(a) 3D representation of \(U_{6}\) with \(\beta\)-derivative for \(\alpha =0.7\), (b) 3D depiction of M-truncated derivative with \(\alpha = 0.7\) for \(U_{6}\), (c) \(U_{6}\) plot in 2D with various derivatives for \(t = 1\).

Full size image
Figure 10
figure 10

(a) 3D figure of \(U_{6}\) with \(\beta\)-derivative for \(\alpha =0.9\), (b) 3D representation of M-truncated derivative with \(\alpha = 0.9\) for \(U_{6}\) , (c) \(U_{6}\) plot in 2D with \(t = 1\).

Full size image
Figure 11
figure 11

2D-depictiin of \(U_{6}\) for multiple derivatives at t=1 for multiple values of \(\alpha\).

Full size image
Figure 12
figure 12

2D-representation with \(\alpha =1\) and \(\beta =0\) of \(U_{6}\) for multiple derivatives.

Full size image

Conclusion

In this article, the vdW equation is studied using beta and M-truncated derivatives. This equation has established solitary wave solutions that exhibit decaying behavior and become unstable when the viscosity \(\eta\) is considered. These soliton solutions were obtained via a new extended algebraic technique along with two different definitions that have taken into account some physical characteristics. Numerous soliton solutions, such as dark solitons, dark singular soliton, dark–bright soliton, and singular solutions of types 1 and 2, have been observed in the described model, along with some constraint conditions. For different values of \(\alpha\), solitary wave solutions with beta formulation behaved differently from the M-truncated derivative, which is found in shape and structure. A 2-dimensional and 3-dimensional plots were also utilized to graphically explain the derived solitons. In comparison to other strategies in the literature, the applied technique was straightforward, short, simple, and easy to implement. It is also very skillful and well developed in terms of generating novel accurate solutions to nonlinear dispersive equations that appear in science and engineering.