Introduction

Turbocharged 12-cylinder diesel engines, which play a central role in Israel Railways (ISR) locomotives, face critical operational challenges, especially in the event of turbocharger failures that can lead to catastrophic explosions. Such failures are often attributed to the compressor impeller, which can break under extreme operating conditions due to excessive centrifugal loads. Several notable cases of such failures have been associated with the engine being operated well above \(\left(\text{26,000} -\text{28,000} RPM\right)\) its normal speed range \((3400- \text{20,000} RPM)\), highlighting the need for accurate estimation of the IAS for preventative fault detection.

Estimating the IAS for these engines is a challenge due to their non-stationary operating conditions. A critical aspect of turbocharger operation in these locomotives is the clutch mechanism. This clutch engages and disengages the turbocharger from the engine, especially at about 60% of engine power, which is normally at \(498 RPM (8.25 Hz)\), resulting in an asynchronous operating phase in which the turbocharger is driven solely by exhaust gas pressure. As a result, the turbocharger can reach higher speeds than the permissible speed, which poses a significant challenge for the accurate estimation of the IAS due to this asynchronous behavior.

Current methods for estimating IAS include various techniques. These include band pass filtering in conjunction with phase demodulation1 and time–frequency analysis (TFA)2. However, phase demodulation reaches its limits when significant speed fluctuations are present when overlapping harmonic components are present. Urbanek et al.3 and Schmidt et al.4 have considered identifying the trajectory with the maximum energy in a Time–Frequency Representation (TFR) as an indicator of an IAS. However, their methods require visual inspection of the TFR and prior knowledge of the rotational speed. Leclere et al.5 introduced a multi-order probabilistic approach (MOPA) to further process the TFRs. Despite its promising improvements, MOPA has difficulty in tracking ridges amidst significant frequency fluctuations6. Another approach such as Peak Search Ridge Estimation (PSRE) and its iterations7,8,9, Cost Function Ridge Estimation (CFRE) and its extensions10,11,12 and Fast Path Optimization Ridge Estimation (FPORE)13,14. These techniques can be divided into two main categories: direct maximum estimation and cost estimation. The former searches for the ridge point with the maximum amplitude at each time instant, but neglects the smoothness of the ridge, which can lead to discontinuous partial curves and noticeable frequency jumps9,10. In the latter, a raw cost kernel function is defined, which is calculated as the square of the frequency jump minus a weighted squared TFR amplitude15,16,17. However, inappropriate weighting settings can affect the performance of ridge estimation18,19, so repeated tuning of the parameters is required. Ridge estimation approaches can also be categorized based on the frequency band search strategy used. Some search for ridge points over the entire frequency range of a TFR13,14 with the risk of interference and lower accuracy due to the complexity of the experimental signal. Others focus on a local frequency band search18,19,20, although they often rely on manual selection and tuning of the search parameters.

Some other methods for IAS estimating such as angular resampling21, machine learning22,23 and time–frequency analysis24 are promising but have their limitations. Machine learning approaches require extensive data for training and are less effective under variable speed conditions. Moreover, some time–frequency methods, offer lower error rates but still struggle with the trade-off between time–frequency and resolution, especially in scenarios with low harmonic content and Signal-to-Noise Ratio (SNR). Davidyan et al.25 have presented an algorithm that overcomes the usual trade-off between time and frequency resolution in estimating IAS from vibration signals. Unlike conventional approaches, this algorithm overcomes the limitation of time–frequency resolution by estimating the IAS directly from the vibration signals, thus significantly improving the resolution of IAS determination. Davidyan et al.25,26 have presented an algorithm that overcomes the usual trade-off between time and frequency resolution when estimating IAS from vibration signals. In contrast to conventional approaches, this algorithm overcomes the limitation of time–frequency resolution by estimating the IAS directly from the vibration signals and requires the input of the basic parameters of the system, while all other parameters controlling the process are determined automatically, thereby significantly improving the resolution of IAS determination. The maximum error found of 0.08%25 reflects the high quality of the algorithm. Table 1 provides a comprehensive overview of the different methods for estimating the IAS and shows the advantages and disadvantages of the individual methods.

Table 1 Summary of methods for estimating the IAS
Full size table

To estimate the IAS and overcome the complex operating conditions of these engines, this study builds on the previously presented algorithm25 and integrates a significant improvement: the 'adaptive de-phasing' step27.The de-phasing method is based on the removal of the phase-averaged signal (or time-synchronous average – TSA)28,29 and effectively eliminates the synchronous elements of the vibration signal, leaving the asynchronous vibrations by removing specific peaks that are synchronous with the diesel engine shaft. The improved algorithm shows higher performance in automatically isolating and cleaning engine-related scenarios from the vibration signature. This advance represents a significant step forward in accurately monitoring and predicting the operating behavior of turbochargers under various and unpredictable conditions and could reduce the risks of turbocharger failures.

The study is divided into five main sections. "Locomotive Turbocharged 12 Cylinders Diesel Engine" introduces the diesel engine used in locomotives. "Enhanced Algorithm for IAS Estimation" describes the development of the improved new algorithm. "Results" validates the algorithm and demonstrates its effectiveness using simulated and experimental data. Finally, the study is summarized in "Summary and Conclusions"

Locomotive turbocharged 12 cylinders diesel engine

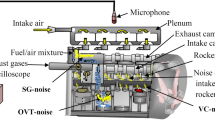
The locomotive is equipped with a turbocharged 12-cylinder diesel engine, as can be seen in Fig. 1. The turbocharged diesel engine is a two-stroke "V-engine that combines the advantages of low weight per horsepower, a positive air scavenging system, solid fuel injection and a high compression ratio. In a two-stroke diesel engine, power is generated on each downward stroke of the piston. During this stroke, the cylinders draw in air through openings in the cylinder wall that open into a chamber that is supplied with compressed air by a rotating impeller. This compressed air effectively expels the spent gasses from the cylinder via several exhaust valves in the cylinder head. As the piston rises, it seals these openings and closes the exhaust valves, compressing the air in the cylinder. At the peak of the stroke, fuel is injected, which spontaneously ignites due to the high compression heat and drives the piston back down until the ports and exhaust valves open again.

Figure 1
figure 1

Locomotive turbocharged 12-cylinder diesel engine scheme.

Full size image

The turbocharger is driven via a gearbox with a transmission ratio of 1:18.3 to the main gear of the diesel engine. The exhaust gases from the engine flow through a manifold and drive the turbocharger's turbine before exiting via the exhaust stack. When starting the engine or at low power, the exhaust gases do not generate enough heat to drive the turbine and impeller sufficiently. Under these conditions, the engine drives the turbocharger mechanically with additional support from the available exhaust gas heat. At higher power levels (60% engine power), the exhaust gas heat alone is sufficient to drive the turbocharger. This triggers an overrunning clutch that separates the mechanical drive from the engine. Under these conditions, only the engine gases drive the turbocharger. The engine and turbocharger speeds are shown in Table.2.

Table 2 Diesel engine and turbocharger rotational speeds.
Full size table

Enhanced Algorithm for IAS Estimation

The IAS estimation algorithm25, was developed for the direct estimation of IAS from the vibration signals of a rotating shaft. It includes two main stages: the Rotational-Speed Curve Search (RSCS) and the Estimation of Rotational-Speed (ERS). A key strength of the algorithm lies in the simplicity of the input requirements, which include the rotational speed range (maximum rate of change and the characteristic frequencies of the rotating components) and at least two harmonics of the rotational speed to be followed for IAS approximate curve determination. The availability of these inputs gives the proposed approach a significant advantage, since most of the algorithm parameters are automatically calculated. In this study, a third stage, the adaptive de-phasing – stage26, is integrated into the original algorithm. The stages are presented in Fig. 2.

Figure 2
figure 2

Enhanced algorithm for IAS estimation flowchart.

Full size image

Rotational-speed curve search (RSCS)

1. In the first step the spectrogram is calculated based on the rotational acceleration \(a\), where \(Fs\) represents the sampling rate, to create the Time–Frequency Representation (TFR).

$$WIN= \frac{Fs}{a}$$
(1)

2. Next, local maxima above the \(90th\) percentile in the predefined frequency range \(\left\{f\in {\mathbb{R}}:H\cdot RPS1\le f\le H\cdot RPS2\right\}\), are extracted to highlight significant ridges.

Where \(H\) is the harmonic number of the rotational speed and \(RPS1\) and \(RPS2\) are the limits of the minimum and maximum rotational speed range.

3. In the third step, the top 10% of the local maxima are filtered to identify continuous harmonic curves of rotational speed that focus on compliance with the predefined acceleration limit. The classification process for the continuous time–frequency curves selection is done as follows:

$$S\left(\tau ,f\right)=|x(n-1,{m}_{1})-x(n,{m}_{2})|\le a$$
(2)

where \(n=\text{1,2},\dots ,\tau\) is the time slot of the TFR and \({m}_{1},{m}_{2}=\text{1,2},\dots ,N\) is the frequency bin of the TFR and \(S\left(\tau ,f\right)\) is a TFR matrix containing the continuous time–frequency curves.

4. In the final step, to relate the extracted curve to the instantaneous rotational speed of the shaft, the curves of a particular harmonic are normalized to the first harmonic and compared using the relative squared difference (SD) between two curves from two different rotational harmonics at each time instant as follows:

$$SD = \sum\nolimits_{i = 1}^{N} {\frac{(\psi \left( i \right) - \zeta \left( i \right))}{{(\psi \left( i \right))^{2} }}}$$
(3)

where \(\psi\) is a curve normalized to the first rotational harmonic from a particular harmonic and \(\zeta\) is a curve normalized to the first rotational harmonic of another (different) harmonic at the \(i-th\) observation.

Estimation of rotational-speed (ERS)

In the ERS phase, the process involves selecting a specific rotational harmonic for estimating the IAS curve. A harmonic with a high SNR and without neighboring peaks is preferred. Using the Time–Frequency (T-F) curve previously estimated in the RSCS stage, the algorithm extracts quasi-stationary IAS curves from the vibration signal. This step includes a filtering process centered around each value of the preliminary T-F curve, which facilitates the precise estimation of the corresponding phasor, as follows:

$${\varphi }_{i}=\Gamma \left(X\left(\Delta t\right),IAS\right) , \Delta t\subset \left[\left(i-1\right)\cdot \frac{Fs}{2\cdot a}+1,\left(i-1\right)\cdot \frac{Fs}{2\cdot a}+\tau *Fs\right]$$
(4)

where, \(X\) is the vibration signal, \(\Delta t\) is time (one second), \(IAS\) is the selected preliminary rotational speed curve values, \(\Gamma\) is the filtering process, \(Fs\) is the sampling rate,\(a\) is the acceleration and \(\tau\) is the TFR time resolution.

Adaptive De – phase

The de-phasing method27 focuses on removing the phase-averaged signal, also known as the Time Synchronous Average (TSA), from the vibration signal. The TSA, which is calculated as the average of segments representing a single rotation of a shaft, eliminates synchronous components by averaging the resampled signal over one rotation cycle. This process results in the exclusion of signal elements that are out of phase with the rotational speed and isolates the periodic elements that correspond to the harmonics of the rotational speed of the shaft. Mathematically, the TSA in the cycle domain, denoted as \(S T{{A}_{x}}_{n}\), for a given rotation frequency \({R}_{1}\) of the cycle history \(x\) is expressed as:

$$S T{{A}_{x}}_{n}=\frac{1}{M}\sum_{i=1}^{M-1}{x}_{n+m,mN} n=1,\cdot \cdot \cdot ,N$$
(5)

where \(N=1/R1\), \(M\) is the number of cycles in the signal and \(S T{{A}_{x}}_{n}\)​ is the vector in \({\mathbb{R}}^{n}\) representing a single cycle.

The phase average STAxn is then replicated to match the size of the resampled signal x, resulting in:

$${y}_{replicated}=S T{{{A}_{x}}_{n}}_{nmodN} n\in {\mathbb{N}}$$
(6)

Finally, removing the phase average removes all effects that are synchronized with the rotational speed \(R1\), resulting in the de- phased signal:

$$\widetilde{x}=x-{y}_{replicated}$$
(7)

In cases involving non-stationary signals characterized by varying amplitudes of synchronous elements due to changes in rotating speeds and operating loads, the method applies an adaptive de-phasing strategy. This adaptive de-phasing approach, referred to in29, was developed to remove the STA within dynamic frames. The adaptive dephasing method involves a cascading removal of the phase average for each specific rotational speed, as shown in Fig. 2. The standard implementation of this algorithm involves resampling the signal according to the rotational speed or phase of each shaft, followed by the de-phasing process using the corresponding STA. For the locomotive diesel engine gearbox where \(K STAs\) corresponding to the synchronous shafts \({R}_{k}=1,\dots ,K\) need to be removed, the procedure is as follows:

  • Resample the raw signal once according to the fastest shaft rotating speed and de—phase the signal by removing the \(STA\) corresponding to this shaft.

  • For all \(K-1\) remaining shafts, interpolate the de—phased signal at intervals matching another shaft speed \({R}_{K}, K=2,\dots ,K\), followed by the removal of its respective \(STA\).

  • Reverse the de—phased signal by interpolation into the desired cycle or time domain.

For Israel Railways locomotive diesel engines, this step is critical once the engine speed exceeds 498 RPM to ensure that the de-phasing process accurately captures the dynamic behavior of the system. The resulting spectrum of a de—phased signal should contain only asynchronous elements as peaks that correspond to the asynchronous tones as the natural frequencies inherent in the structural composition.

Results

The proposed algorithm was tested with two data sets: a dataset with simulated signals and a dataset measured on a locomotive diesel engine. The simulated dataset was chosen because it allows full control over the data elements. The locomotive dataset was selected because estimating the IAS for these engines is challenging due to their non-stationary operating conditions.

Simulated dataset

The vibration signal is modeled as follows: Consider \({S}_{1}, . . ., {S}_{k}\) as the rotating speeds for a set of \(N\) shafts in a simulated system. Corresponding phase functions are represented by \({U}_{1}, \dots , {U}_{N}.\) For each shaft indexed by \(j\), the relative frequencies, are represented by \({\theta }_{j,1}, \dots , {\theta }_{j,{C}_{j}}\) for the \({C}_{j}\) parts mounted on the shaft. The corresponding phase shifts for these parts are given by \({h}_{j,1}, \dots , {h}_{j,{C}_{j}}\). The phase \({\beta }_{j,i}(t)\) for each rotating part is thus expressed as \({\beta }_{j,i}(t) ={\theta }_{j,i}{U}_{j}(t) + {h}_{j,i}\). The composite signal can then be formulated as follows:

$$x(t)=\frac{1}{M}\sum_{i=1}^{N} \sum_{i=1}^{{C}_{j}}{A}_{ji}\text{cos}\left({\beta }_{j,i}\left(t\right)\right)+n(t)$$
(8)

where \(n(t)\) represents white noise and \({A}_{ji}\) signifies the amplitude associated with each rotating part's signal. In a physical system, the excitation due to rotating components, denoted by \(x(t)\), propagates to the sensor through the structural transfer function of the machinery, \(h(t).\) This function selectively amplifies different frequency bands, yielding the sensor's response \(y(t) = x(t)*h(t).\) The signal observed at the sensor is therefore characterized by:

$$y\left(t\right)=x\left(t\right)*h\left(t\right)=\left(\frac{1}{M}\sum_{i=1}^{N} \sum_{i=1}^{{C}_{j}}{A}_{ji}\text{cos}\left({\beta }_{j,i}\left(t\right)\right)+n\left(t\right) \right)*h(t)$$
(9)

where \(*\) denotes the convolution operation, and \(h\left(t\right)\) represents the impulse response of the system's transfer function.

In this study, two simulated signals were generated with different rotational speed profiles, as shown in Table 3.

Table 3 Simulated rotational speed profiles.
Full size table

Using the different speed profiles, different simulated signals were generated based on a rotating machine consisting of a 15-tooth pinion meshing with a 35-tooth gear, a bearing with outer ring spalling corresponding to an order of 3.6 and the corresponding pinion shaft. All simulations were performed at a sampling frequency of 5 kHz and included a SNR of 10 dB due to additional white noise. The generated signal contained components that were synchronised with the speed of the shaft \({S}_{1}\) and had different amplitudes at harmonics 1, 2 and 3. In addition, gear-like components with mesh orders 1, 3 and 7 were integrated with FM (frequency modulation) over the respective speeds. All amplitudes of the synchronous elements \({A}_{j,i}\) were constant. In the simulation, all signals were convolved with an impulse response. Each data set had a duration of 40 s. To define the speed range, the lower and upper limits were set to capture the first harmonics of the speed profiles:6,21 Hz. In addition, white noise with a standard deviation of about 0.035 Hz was superimposed on each speed profile to simulate real conditions. The same shaft harmonics (1, 3, 5 and 12) of each speed profile were used to estimate the IAS for all simulated signals. In addition to the conditions checked by the algorithm ("Rotational-Speed Curve Search (RSCS)"), a correlation between several characteristic frequencies of the rotating parts of the system was established by using several harmonics of the rotating shaft, which ensures a reliable and accurate IAS estimation and eliminates the risk of influencing rotating components such as the crankshaft, oil pump and water pump.

Figure 3a and Fig. 3b show the estimated simulated speed for all speed profiles. Figure 3a serves as a critical basis for evaluating the effectiveness of the proposed algorithm in estimating the speed. The black curve in Fig. 3a and Fig. 3b represents the actual (simulated) instantaneous frequency, while the red curve in Fig. 3a and Fig. 3b represents the IAS estimated by the proposed algorithm. The Root-Mean-Square Errors (RMSEs) between each estimated IAS and the simulated IASs are 0.2637 for profile 1 and 0.4389 for profile 2 and were calculated as follows:

$$RMSE=\sqrt{\frac{1}{n}\left(\sum_{i=1}^{n} ({s}_{i}-\widehat{{s}_{i}}\right)}$$
(10)

where \(n\) is the number of observations, \({s}_{i}\) is the simulated speed at the \(i-th\) observation and \(\widehat{{s}_{i}}\) is the speed estimated by the algorithm at the \(i-th\) observation.

Figure 3
figure 3

Estimated instantaneous speed profiles for each method based on the simulated data. (a) Profile 1, (b) order spectrum of the simulated vibration signal (profile 1) and the phase signal, (c) profile 2, (d) order spectrum of the simulated vibration signal (profile 2) and the phase signal.

Full size image

As can be seen from Fig. 3a and Fig. 3b, the proposed algorithm achieves good results and agrees very well with the simulated IASs. From Fig. 3a and Fig. 3b, the proposed algorithm is able to effectively detect the ridge with strong frequency variations even under such conditions where harmonics tend to be smeared in the TFR and are difficult to distinguish. However, it should be noted that there is a slight deviation between the simulated speed and the estimation of the proposed algorithm towards the end of the study duration (time = 40s). Figure 3c and Fig. 3d show the comparison of the order spectrum between the simulated vibration signals and the de—phased vibration signals. The reduction of the peaks corresponding to the main shaft (\({S}_{1}\)) of the simulated system and the interactions with the gearbox to a level close to the background noise level in the de—phased signal emphasises the effectiveness of the de—phased stage. It is also important to note that the de-phased signal retains the small dip at order 0.5 in the simulated signal profile. This is because the algorithm specifically targets and suppresses synchronous components that are multiples of the rotational speed. Since the order 0.5 is not a synchronous multiple, it remains unaffected by the de-phasing process. This distinction illustrates the ability of the algorithm to suppress synchronous harmonics, which is a fundamental feature of the analysis approach used. The ensemble of Fig. 3a–d is a robust demonstration of the versatility and consistent reliability of the algorithm under different simulated speed profiles. These visual analyses demonstrate the algorithm's comprehensive ability to accurately estimate IAS and confirm it’s potential to make an important contribution to the field of mechanical systems and signal processing.

Locomotive diesel engine dataset

To validate the proposed algorithm, field tests were conducted with a locomotive. The locomotive diesel engine was equipped with two vibration sensors strategically placed at critical points on the turbocharger housing, as can be seen in Fig. 1 and Fig. 4. The test protocol included both stationary and dynamic assessments. In the steady-state tests, recordings were taken continuously as the throttle was moved incrementally through its eight positions. This procedure was designed to allow the engine speed to reach a steady state at each stage before the test continued. In contrast, the dynamic tests recorded the engine's response to free acceleration, where the throttle was opened abruptly from the lowest to the highest position and the engine accelerated until the engine speed reached a plateau. In addition, the engine's performance was recorded at variable throttle transitions, as specified by the driver, until a stable engine speed was observed. These comprehensive tests provided robust data sets to evaluate the effectiveness of the algorithm under real-time conditions covering a wide range of operating conditions. The sampling rate of the accelerations was set to 5 kHz. The algorithm was set to track the IAS curve of the engine and turbocharger within a frequency window in the TFR of \(3.33-16 Hz\) and \(266-333 Hz\) respectively.

Figure 4
figure 4

Experimental set up. Two vibration sensors were mounted to the locomotive diesel engine.

Full size image

Figure 5 shows the experimental results obtained when the locomotive driver turned the throttle up to the maximum, level 8. Under these conditions, the rotational speed of the diesel engine should be around \(900 RPM (15\pm 0.5 Hz)\), a condition in which the turbocharger is driven solely by the exhaust gas pressure, with the clutch disengaged. If no overspeed scenario occurs, the turbocharger rotational speed should be between \(\text{16,000}\) and \(\text{20,000} RPM (266-333 Hz)\), depending on the engine load. Figure 5a shows the spectrogram of the vibration signal recorded during the steady-state test. It shows a spectrum rich in different frequencies, such as the main shaft of the diesel engine and its harmonics, the gear meshes and the turbocharger harmonics. Figure 5b shows the estimated IAS curve of the main shaft of the diesel engine, which corresponds to the expected frequency range of about \(15\pm 0.5 Hz\). Figure 5c show the estimated IAS in detail. In particular, Fig. 5c confirms the precision of the algorithm, as the calculated rotational speed is \(913 RPM\), which is consistent with the operational expectations for the given throttle setting.

Figure 5
figure 5

Experimental results. (a) Spectrogram of the vibration signal (b) first harmonic of the diesel engine IAS, (c) extracted IAS curve from the TFR, (d) estimated IAS of the diesel engine.

Full size image
Figure 6
figure 6

Experimental results. (a) Order spectrum of the original vibration signal (blue) and the phase signal (red), (b) spectrogram of the de-phased signal, (c) extracted IAS curve from the TFR, estimated IAS of the diesel engine and the turbocharger.

Full size image

In order to estimate the IAS of the turbocharger under these operating conditions (throttle up to the maximum, level 8), the vibration signal is subjected to a dephasing process to attenuate the influence of the amplitudes of the synchronizing elements. The effectiveness of this process is shown in Fig. 6. Figure 6a shows the comparison of the order spectrum between the original and the de—phased vibration signal. The reduction of the peaks corresponding to the main shaft of the diesel engine and the interactions with the gearbox to a level close to the background noise levels in the de—phased signal underlines the effectiveness of de—phase stage. Figure 6b shows the spectrogram of the de-phased signal, in which a clear asynchronous frequency band between \(266-333 Hz\) can be seen. This frequency band is identified as the first harmonic of the turbocharger. Figure 6c shows the performance of the algorithm when the extracted IAS curve in matches the targeted frequency band. The resulting speed, given as \(\text{16,042} RPM\), corresponds to the expected performance of the turbocharger at the specific throttle position.

Figure 7 shows the estimated IAS of the turbocharger during the dynamic test. As can be seen in Fig. 7, there are a series of distinct plateaus, each corresponding to the throttle positions during the dynamic phase of the test. The step changes reflect the response of the engine, which stabilizes at each throttle position. These results demonstrate the effectiveness of the algorithm in resolving the IAS from the complex vibration signals under the varying load conditions that occur during the dynamic and stationary phases of locomotive operation. The precision with which the IAS is captured, even under the challenges of operational variability, underlines the potential of the algorithm to improve predictive maintenance and ensure the reliability of locomotive operation.

Figure 7
figure 7

Dynamic experimental results. Estimated IAS of the turbocharger under varying load conditions.

Full size image

Summary and conclusions

In this study, an enhanced algorithm for estimating the IAS of turbocharged diesel engines directly from vibration signatures is proposed. The algorithm works in a three-stage procedure. First, the rotational speed is approximated in distinct time segments and the estimated curves are validated using criteria such as continuity and correlation with characteristic frequencies in the time–frequency domain. In the second phase, the phasors for each time segment are extracted using a cascade band pass filters to minimize edge effects. These phasors from different segments are then merged into a comprehensive phasor for the entire signal duration, which facilitates the extraction of the IAS using established methods. An important innovation in the third stage is the implementation of a de-phasing process. This process effectively removes synchronous components by averaging the resampled signal over one revolution cycle, allowing the IAS of a diesel engine turbocharger to be estimated. The input requirements of the algorithm are minimal and require basic system parameters such as the range of rotational speed variability, the maximum rate of change in Hz/s and the characteristic frequency multipliers of the rotating components. For the second stage, the specification of a single characteristic frequency for the phasor extraction is sufficient. This algorithm, which has been validated with simulated and experimental data, proves to be effective for non-stationary rotational speeds and is adaptable to any range of rotational speeds and rates of change. Its robustness is attributed to the correlation between several characteristic frequencies of the rotating parts of the system, which ensures reliable and accurate IAS estimation in dynamic operating environments. Furthermore, the algorithm is not limited to 12-cylinder diesel engines or rail vehicles, but can also be applied to a wide range of diesel engines, including 16-cylinder configurations. This versatility makes the algorithm suitable not only for locomotives, but also for various other rotating machinery, such as marine engines and power plants, underlining its wide applicability in industrial maintenance and operations.