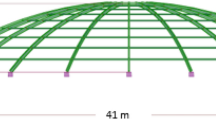
Abstract
Geodesic domes are structures which deliver effective solutions, associated with cost savings, due to the lack of intermediate supports when roofing large-sized objects. The multitude of advantages of this type of construction was translated into the shaping of innovative lightweight objects of geodesic domes, constructed on a regular octahedron. In this article, the use of strut sections was applied to covers generated due to a regular octahedron. Two families of domes were compared, resulting from the use of two methods that differ from each other in their topology. Each family consist of 8 structures thus finally 16 geodesic domes were considered. The generated domes were compared in terms of the same section for all strut elements, and the optimized section for each group of struts. To find the design focused on obtaining optimal solution, a number of comparative analysis were carried out. The presented analysis is extremely important in the context of environmental impact, because it shows the steel consumption and the sense of optimization. It was indicated that by optimizing the cross-sections of the strut elements, the steel consumption, as well as their weight, decreased by approx. 10–25% for dome structures which were created using method 1 and 20–40% for domes generated using method 2. The article aims to provide suggestion on the selection of the appropriate innovative geodesic dome mesh. A mesh based on various methods of shaping the covers of geodesic domes created using a regular octahedron.
Similar content being viewed by others
Introduction
Geodesic domes are structures that are widely used as architectural forms due to their numerous advantages. They are innovative structures which provide many benefits in terms of strength, durability, energy efficiency, cost efficiency and sustainability. Covering of very large areas without using internal supports, relatively low weight resulting from the savings of the material used (steel), economic solutions as well as less heating and cooling requirement are features that undoubtedly distinguish this type of structures from other forms. The shape of geodesic domes also satisfies the aesthetic requirements of the society.
The variety of geodesic dome shaping is huge. The topology of connection of strut elements allows for obtaining many different covers of geodesic domes. Providing the designer with an effective suggestion as to the possible geometry of the designed geodesic-like dome structure was presented by Shaw et al.1 by developing a computing system.
Sustainable and efficient cross-sections of strut elements using allow for optimized structures while ensuring all structural requirements. The topic of optimization of domes has been widely recognized in the works of other authors, from the point of view of various aspects. Shrivastava and Pendharkar2 considered geodesic domes generated from icosahedron, with different cross-sectional shapes i.e. rectangular, square and circular. The authors indicated the case with the lowest and highest stresses among the three sections considered. The Colliding Bodies Optimization (CBO) and its enhanced version (ECBO) for optimum design of Schwedler and ribbed domes were presented by Kaveh and Rezaei3. In other work, Kaveh and Talatahari4, applied the Charged System Search, that is the meta-heuristic algorithm. Thank to that they obtained the optimum design of analysed geodesic domes. Different approach was taken by Saka 5, thanks to which the optimum number of rings, height and cross-section for struts of dome were considered. To improve stability, Ye and Lu6 established an optimization model against instability. Kaveh et al.7 showed Shuffled Shepherd Optimization Algorithm (SSAO) as an approach to optimal design of the large-scale space structures. Artar8 used two powerful metaheuristic search techniques, that is harmony search and genetic algorithms, to design the minimum weight of different analysed truss structures. The author’s aim was to choose the suitable cross-section of profiles. The optimization process covers a number of different issues, which was indicated, among others, by Aslay and Dede9 by developing the ACDOS programming, referring it to the reinforced concrete structure of the 7-story public dormitory building.
Another aspect worth paying attention to is the optimization of gridshells. Argento et al.10 presented shape optimization of a bi-parabolic shell roof. The authors also focused on improving local shape control in the optimization process using isogeometric refinement. A novel and efficient shape optimization framework for freeform gridshell designs was the subject of paper by Ding et al.11. Zuo et al.12 concentrated on steel joints in gridshells, proposing topology optimization, numerical analysis and additive manufacturing workflow process. Bertetto et al.13 indicated a form-finding method that is specifically designed for gridshell structures. They used the Multi-body Rope Approach (MRA) for this purpose. Mesnil i Baverel14 proposed the concept of pseudo-geodesic gridshells, where planks follow pseudo geodesic curves of a surface, indicating that the structural efficiency of pseudo-geodesic gridshells may be twice as much as geodesic gridshells. To improve the static, nonlinear stability and economic performance of free-form latticed shells, Xu et al.15 proposed a novel RBF-NSGA-II optimization framework based on the response surface methodology (RSM) and the constrained NSGA-II algorithm to find a shape with the minimum strain energy. At the same time, they emphasized that the proposed method can be used in the design of the cable-stiffened latticed shells. Tomei16 dealt with issues related to appropriate design based on optimization techniques to guarantee light solutions safe from global buckling phenomena. The author proposed the joint stiffness approach and the rigid/hinged approach. At the same time, he showed the beneficial effect of a finite value of the rotational stiffness of the joints in the susceptibility of the gridshell to global buckling phenomena, leading to light structural solutions. Raffaele et al.17 indicated the issues related to the performance of gridshells, based on three gridshells with their spring line partially unconstrained, and to their fully-constrained counterparts. The optimization aspect was also addressed by Wang and Wu18 in relation to cable-stiffened latticed shells, indicating a method by which the global optimal shape of the gridshell can be obtained. Tomei et al.19 pointed out the pre-tensioned rods in the gridshell structure, which influence the optimization of the gridshell structure, and also proposed a procedure for optimizing this type of design solutions.
The aspect of global buckling has been thoroughly analyzed in the world literature. In the paper of Yan et al.20 the authors investigated the interaction between the member buckling and the overall buckling on the basis of eight types of different dome’s grids. Progressive instability, as well as synchronous instability were analysed. The detailed state-of-the-art of the buckling problems was presented by Gioncu21. The paper by Lenza22 presented the aspect of structural failure through the instability of the entire structure caused by the phenomenon of rod buckling.
Considering strut domes in terms of dynamic behavior was addressed, inter alia, by Barbieri et al.23 as well as Roopa et al.24. The optimization of the small, medium and large-scale domes subjected to the multiple dynamic constraints was presented by Dede et al.25,26. In turn, preliminary research on the dynamic loads of domes derived from a regular octahedron, which are the subject of this article, was presented by Bysiec et al.27. The seismic response to structures created on the basis of a regular octahedron has also been initially analysed by Bysiec and Maleska28,29.
This article focuses on the geodesic dome coverings. These are innovative structures, recognized by the author (Pilarska30, Bysiec31, Bysiec et al.32), due to the basis of their formation. Their structure is based on a regular octahedron, while the previous scientific considerations are based mainly on the regular dodecahedron or icosahedron. The author described many innovative structures, taking into account the use of several groups of struts in each recognised dome. This article is a scientific consideration of the efficiency of the applied cross-sections of groups of strut elements for 16 innovative structures, generated according to different methods of creating topology of geodesic domes with one type of struts in compare to domes with few groups of struts. In this paper the displacements, tension forces, compressive forces and impact of weight were analysed. It shows the effective use and at the same time the reduction of the construction material used (steel).
The use of a regular octahedron to create dome covering structures
Description of methods of creating the analysed domes
Previous research papers on geodesic domes focuses on the regular icosahedron or regular dodecahedron. This is due to the higher symmetry and repeatability of elements that can be achieved compared to meshes based on other polyhedra. This fact was proved by the American designer Richard Buckminster Fuller, who presented a description of the procedure for the subdivision of the sphere into spherical triangles on the example of an icosahedron as the basis polyhedron in US Patent 2,682,235 of 29 June 1954. However, other polyhedra, including the regular octahedron, can also form the basis for generating geodesic dome meshes, which is a new approach to this problem. This fact, according to the author, should be thoroughly analyzed and expanded, thus confirming the validity of using the remaining polyhedra to shape the structures of geodesic domes. The author, in her earlier works (Pilarska30, Bysiec31, Bysiec et al.32) presented in great detail the methods used to generate the lightweight geodesic domed coverings based on the regular octahedron, which are the subject of this work. These methods allowed for the creation of structures that had not been recognized before. They are strut domes, the basis of which is a regular octahedron, not identified polyhedra for generating geodesic domes so far. Thanks to the methods used, two families of domes were designed: 8 structures derived from method 1 and 8 structures created due to method 2 (Table 1).
To create the structures of the analysed geodesic domes, two different methods of dividing a spherical triangle, which is the base face of a regular octahedron, were used. By interpolating a flat face of an octahedron in the form of a triangle, the division points were obtained, which were projected by radial rays onto the surface of the sphere concentric with the polyhedron. In method 1, a mesh of steel struts of the dome was created by dividing each triangular side into n parts and drawing three families of lines parallel to the sides of the initial face of the regular octahedron. By dividing the initial edge of the triangular face of a regular octahedron into two parts, we obtain a derived polyhedron, half of which is the mesh of a geodesic dome created on the basis of a 32-hedron. This is the „2V” mesh which is shorthand of “frequency 2", shown in Fig. 1a. Similarly, by increasing the frequency of dividing the initial edge of the regular octahedron, we obtain subsequent derivatives reflecting increasingly denser meshes of geodesic domes created according to method 1. Figure 1b shows a „3V” mesh ("frequency 3"), which is a dome generated on the basis of a 72-hedron, while Fig. 1c shows a „4V” mesh ("frequency 4"), which is the basis for creating a geodesic dome from a 128-hedron. In method 2, unlike method 1, three families of parallel lines were drawn to the height line. Moreover, in method 2, the number of division frequencies of the initial edge of the regular octahedron is an even number. The division into 2 parts forms a dome generated on the basis of 24-hedron (“2V”, "frequency 2"), as shown in Fig. 1d, the division into 4 parts is a dome mesh based on 96-hedron (“4V”, "frequency 4"—Fig. 1e), while increasing the number of divisions to 6 guarantees the creation of a dome mesh with a base of 216-hedron (“6V”, "frequency 6"—Fig. 1f). The use of an increasing number of dividing the initial edge of a regular octahedron guarantees obtaining grids of geodesic domes with an increasing density of struts. This applies to both methods used, assuming that in method 2 the number n frequency must be an even number. A graphic comparison of both methods is shown in Fig. 2. Examples of strut geodesic domes being the subject of this study are shown in Fig. 3.
Description of numerical models
The shaped structures of the covers were analysed in terms of statics using the Autodesk Robot Structural Analysis program. Thanks to the Finite Element Method used by the program, comprehensive calculations can be performed effectively, which definitely affects the final results of the analysis of engineering structures. The subject of numerical analyses were 16 innovative lightweight domed structures. Based on Eurocode 3, cross-sections in the form of round tubes made of commonly used structural steel S235 were proposed for all strut elements, with the following physical properties: Young’s modulus E = 210 GPa, Poisson’s number ν = 0.3, density ρ = 7800 kg/m3. A linearly elastic material was taken into account while maintaining its isotropy. In addition, truss finite elements were adopted (no torsion effect). The use of all the above assumptions and the properties of the construction material allowed for the correct mapping of the work of the modelled domes, taking into account the given load.
In the first stage of the research, an identical tubular cross-section was assigned to all strut elements of the individual analyzed 16 geodesic domes, in accordance with the Eurocode 3 design standard for steel structures33, taking into account the maximum use of the load-bearing capacity in the most stressed strut in the range from 0.80 to 1.00 (Table 2).
In order to indicate the legitimacy of reducing the consumption of construction material (steel), as well as the weight of the analyzed 16 geodesic domes in the second stage of research, 4 groups of struts were distinguished in each analysed structure. Then, the specified groups were assigned different cross-sections. Thanks to this, the analysed domes were designed as skeletal structures using a steel cross-section under a static load of 90%, in accordance with Eurocode 333 (Table 3). The domes were subjected to constant loads and variable loads. The constant loads included self-weight and LSG glass (Laminated Safety Glass) with resistance class P6B, mounted at points in the nodes of the steel structure with a nominal thickness of 23.04 mm, with a characteristic weight gk = 0.58 \(\left[\frac{\text{kN}}{{\text{m}}^{2}}\right]\). Generation of snow for zone 2 and wind loads on the analysed domes with a circular base was carried out in accordance with Eurocode 134. For the snow load analysis, the roof shape factor was adopted based on cylindrical roofs. The case of both even and uneven snow distribution on the dome was considered, assuming, in accordance with the recommendations of Eurocode 134, the maximum value of the coefficient μ3 = 2,00. The included cases are shown in Fig. 4.
Based on Fig. 7.12 of Eurocode 134, the external pressure value coefficients cpe,10 were selected for domes on a circular projection, and the internal pressure coefficients were selected based on note 2 in Sect. 7.2.9 of Eurocode 134 with the values + 0.20 and − 0.30.
Combinations were developed, taking into account the mentioned permanent and variable loads, in accordance with Eurocode35. The load combinations at the ultimate limit state were analyzed taking into account cases of permanent or transient design situations. The following load combination cases were considered: (i) wind load with accompanying snow load (4 cases), taking into account the reduction factor for snow \({\uppsi }_{0}=\text{0,70}\), (ii) snow load with accompanying wind load (4 cases) taking into account the reduction factor for wind \({\uppsi }_{0}=\text{0,60}\). In addition, a quasi-permanent load combination at the serviceability limit state was taken into account to determine the impact of long-term effects. For the serviceability limit state, load cases were considered as for the ultimate limit state, taking into account reduction factors in accordance with standard recommendations for snow \({\uppsi }_{\text{2,1}}=\text{0,2}\) and for wind \({\uppsi }_{\text{2,1}}=\text{0,0}.\) These assumptions of numerical model were similar as in papers of Pilarska30 and Bysiec31.
Results and discussion
Vertical displacements
In applied 1 and 2 methods, the vertical displacements are smaller in the domes, where all struts have the same cross-section (Fig. 5a, b). The coverings created according to method 1, having optimized cross-sections of the struts, show an increase in vertical displacements by 10–45% compared to the same dome structures, but consisting of identical cross-sections of all the struts that make up them (Fig. 5a). A similar tendency is marked in relation to designed covers using method 2. Here, the increase in vertical displacements for domes, the strut sections of which have been optimally matched, ranges from 11–24% (Fig. 5b). Smaller vertical displacements occur in domes created according to method 1, both with the same cross-sections of all elements and with optimized cross-sections (Fig. 5c, d). In the case of the same cross-sections, the difference is at the same levels for all displacements for the analysed domes and amounts to 40–50% (Fig. 5c). Designing optimal cross-sections of struts influences variable differences in the level of maximum vertical displacements. They depend on the degree of structure approximation. The compared middle domes show a difference in maximum displacements of only about 10%. The remaining compared structures indicate approx. 30–40% greater vertical displacements for covers formed according to method 2. In the last pair of domes compared, it is possible to notice about 70% greater maximum vertical displacements (5408-hedron: 3.3 cm and 7776-hedron: 5.6 cm) (Fig. 5d). This means that the topology of creating strut dome structures has an influence on the values of the maximum vertical displacements.
Horizontal displacements
The use of the same cross-sections of strut elements is reflected in significantly smaller maximum horizontal displacements for both the lightweight covers formed according to 1 and 2 methods (Fig. 6a, b). Using method 1of the division, the maximum horizontal displacements increase by more than 100% for the first two designed structures (2888-hedron and 3200-hedron). The next dome shows a difference of about 90%. The greater approximation of triangular face of the octahedron, the smaller differences in the values of the maximum horizontal displacements between the structures having the same cross-section of all struts and optimized cross-sections (Fig. 6a). Method 2 of creating domes shows a similar tendency to method 1, indicating much smaller maximum horizontal displacements in the case of domes having identical cross-sections of all strut elements. The biggest difference in these displacements is approx. 120% for the first designed structure (2904-hedron), while the dome derived from 4056-hedron is characterized by 100% greater horizontal displacements. For the other domes considered, the maximum level of horizontal displacements are greater by approx. 60–70% after the use of optimized cross-sections of strut elements (Fig. 6b). Comparing the analysed lightweight covers formed according to 1 and 2 methods, it can be seen that both with the same cross-sections of all the struts and with optimized cross-sections, the domes generated according to method 1 show smaller maximum horizontal displacements. When analyzing structures with the same cross-sections, the difference is up to 20%. In two cases, horizontal displacements with the maximum values are at the same level. However, in one case (comparing 4232-hedron with 5400-hedron) the difference is greater and amounts to 40% (Fig. 6c). A very similar tendency is for domes with optimized cross-sections of strut elements. The maximum level of horizontal displacements is higher by approx. 10–20% for domes formed according to method 2, in one case these displacements are identical (comparing 5000-hedron with 6936-hedron), while only for domes created according to 4232-hedron and 5400-hedron this difference is greater and amounts to 32% (Fig. 6d).
Tensile forces
The change of sections for struts in particular groups leads to a slight increase in the tensile forces. For structures generated due to method 1, the increase in tensile forces obtained thanks to the use of optimal strut sections was recorded at the level of approx. 3–6% compared to the maximum values of these forces for identical sections of entire domes (Fig. 7a). In method 2, this increase is at the level of 3–10% (Fig. 7b). When analysing the topology of shaped structures of geodesic domes, it can be noticed that it also affects the values of axial tensile forces. When comparing the structures created due to 1 and 2 methods, using the same cross-sections of the strut elements as well as the optimal cross-sections, an increase in the value of tensile forces for covers generated in accordance with method 2 is visible (Fig. 7c, d). Moreover, this difference is bigger and bigger for structures with an increasing density of the initial octahedron mesh with additional strut elements. Taking into account the same cross-sections of the strut elements, each successive pair of domes compared indicates ever greater values of axial tensile forces for domes prepared based on method 2. The biggest difference for the most dense meshes of the analysed domes is at the level of 28% (Fig. 7c). A similar tendency is maintained for domes whose cross-sections of strut elements have been optimized. Here, for the structures with the highest density of strut elements, the maximum axial tensile forces are greater for method 2 by approx. 25% (Fig. 7d).
Compressive forces
Designing the optimal cross-sections of the struts for all created strut domes, both according to 1 and 2 methods, resulted in an increase in the maximum values of compressive forces. With the same cross-sections of the struts, the compressive forces are lower by approx. 8–35% for the structures generated according to method 1 (Fig. 8a) and 6—20% for the structures whose shaping was based on method 2 (Fig. 8b). Looking at the maximum values of the compressive forces in terms of the method of creating structures, both for the same sections for all strut elements and for optimized sections, higher maximum compression forces arise in domes formed due to method 2 (Fig. 8c, d). With the same cross-sections of all elements, the values of compressive forces are higher by approx. 30–70%. The greater the density of elements in the created domes, the greater the difference (e.g. when comparing 5408-hedron and 7776-hedron, the difference is 67.2%) (Fig. 8c). In method 2, the tendency is similar, so larger differences in the values of the maximum compressive forces between 1 and 2 methods show more domes with the greater density of struts. These differences indicate higher values of compressive forces in the applied method 2. Their increase is at the level of 10–50% in relation to the method 1 used (Fig. 8d).
Weight of geodesic domes
Strut domes are light structures, so optimizing the weight of this type of cover is a very important aspect when choosing the appropriate geodesic dome form. Additionally, optimizing the cross-sections of the strut elements shaping a given structure, in consequence, undoubtedly influences its weight. When comparing the weight of structures where all strut elements have the same cross-section with structures with optimized cross-sections, a weight reduction of 10–25% for covers created taking into consideration method 1 (Fig. 9a) and 20–40% for domes generated based on method 2 (Fig. 9b) is visible. The methods of topology for creating geodesic domes from a regular octahedron used in the work indicate that covers formed due to method 1 are less heavy, considering both identical cross-sections of strut elements and optimized cross-sections. Only the first two pairs of compared domes (2888-hedron and 2904hedron, as well as 3200-hedron and 3456-hedron) show the opposite tendency, i.e. the used method 1 points out that structures are heavier than those whose topology is derived from method 2 (Fig. 9c,d). The subsequent comparison pairs of domes indicate that as the number of strut elements in the designed structures increases, the difference in weight between 1 and 2 methods grows, and the domes from method 2 become heavier and heavier. For the last two compared structures (5408-hedron and 7776-hedron), the covers derived from method 2 are heavier by 43% for the same cross-sections of struts and 18% for the optimized ones (Fig. 9c,d).
Conclusions
The use of a regular octahedron can have a large impact on the effective shaping of geodesic dome covers, i.e. covers whose structure is very desirable for large areas, such as shopping centres, exhibition halls, stadiums, etc. To develop the considered domes, two methods of creating their meshes were used in the work. The cross-sections of the strut elements of the designed covers were optimized. Based on that, some important results are summarized as:
-
The process of selection of effective cross-sections of elements in particular groups of the considered domes allows to obtain structures with lower material consumption and, consequently, less weight by approx. 10–25% for domes in method 1 and 20–40% for domes in method 2.
-
The process of selection of effective cross-sections of elements in particular groups of the considered domes allows to obtain structures with lower material consumption and, consequently, less weight by approx. 10–25% for domes in method 1 and 20–40% for domes in method 2.
-
The static analysis shows that the strut domes in method 1 are characterized by: (i) less displacements of nodes in vertical direction both for the same strut sections (by approx. 40–50%) and for optimized sections (by approx. 30–40%), (ii) less displacements of nodes in horizontal direction, about 10% for the same strut sections and 10—20% for optimal sections, (iii) lower values of axial tensile forces by approx. 28% for domes whose strut elements have the same cross-sections, and approx. 25% for optimized sections, (iv) lower values of axial compressive forces for both considered cases, i.e. approx. 30—70% lower for structures with identical cross-sections of struts and 10—50% for domes with optimized sections.
-
The optimisation of steel structure is very important and have significant impact on the steel consumption in civil engineering, also on the environmental.
Finally, it can be concluded, that this type of numerical analysis can be useful for the engineering during designing, construction process and maintenance service. The proposed innovative structures, thanks to their aesthetic considerations, can undoubtedly also be the basis for choosing the appropriate form of cover for architects. In addition, in the nearest future, a very interesting point may be the development of the preliminary analysis of the dynamic behavior of geodesic domes. Thus, the author will try to find an answer to the question "what is the impact of seismic excitations in relation to structure of geodesic domes". The aspect of locating the additional masses seems interesting. The mentioned masses can disrupt the apparently ideal structure of the domes and lead to completely different responses.
Data availability
The datasets generated during and/or analyzed during the current study are available from corresponding author on reasonable request.
References
Shaw, D., Miles, J. & Gray, A. Conceptual design of ‘Geodesic-like’ domes using computational geometry. Archit. Eng. Des. Manag. 3(4), 238–248. https://doi.org/10.1080/17452007.2007.9684645 (2011).
Shrivastava, A. & Pendharkar, U. Study of optimised sectional shape for geodesic domes. J. Xian Univ Archit Technol. 13(1), 407–411 (2021).
Kaveh, A. & Rezaei, M. Topology and geometry optimization of single-layer domes utilizing CBO and ECBO. Sci. Iran 23(2), 535–547 (2016).
Kaveh, A. & Talatahari, S. Geometry and topology optimization of geodesic domes using charged system search. Struct. Multidiscipl. Optim. 43, 215–229. https://doi.org/10.1007/s00158-010-0566-y (2011).
Saka, M. P. Optimum topological design of geometrically nonlinear single layer lattices domes using coupled genetic algorithm. Comput. Struct. 85(21–22), 1635–1647. https://doi.org/10.1016/j.compstruc.2007.02.023 (2007).
Ye, J. & Lu, M. Optimization od domes against instability. Steel Compos. Struct. 28(4), 427–438. https://doi.org/10.12989/scs.2018.28.4.427 (2018).
Kaveh, A., Zaerreza, A. & Hosseini, S. M. An enhances shuffled shepherd optimization algorithm for optimal design of large-scale space structures. Eng. Comput. 38, 1505–1526. https://doi.org/10.1007/s00366-021-01292-z (2022).
Artar, M. A comparative study on optimum design of multi-element truss structures. Steel Compos. Struct. 22(3), 521–535. https://doi.org/10.12989/scs.2016.22.3.521 (2016).
Aslay, S. E. & Dede, T. Reduce the construction cost of a 7-story RC public building with metaheuristic algorithms. Archit. Eng. Des. Manag. https://doi.org/10.1080/17452007.2023.2195612 (2023).
Argento, G. R., Varano, V., Marino, E. & Gabriele, S. Shape optimization of shells: an R-Funicularity based approach. Structures. 66, 106831. https://doi.org/10.1016/j.istruc.2024.106831 (2024).
Ding, C. et al. An efficient and robust shape optimization framework for gridshell designs based on node shifting method. Structures 62, 106209. https://doi.org/10.1016/j.istruc.2024.106209 (2024).
Zuo, W. et al. Additive manufacturing oriented parametric topology optimization design and numerical analysis of steel joints in gridshell structures. Thin-Walled Struct. 188, 110817. https://doi.org/10.1016/j.tws.2023.110817 (2023).
Bertetto, A. M., Melchiorre, J. & Marano, G. C. Improved multi-body rope approach for free-form gridshell structures using equal-length element strategy. Autom. Constr. 161, 105340. https://doi.org/10.1016/j.autcon.2024.105340 (2024).
Mesnil, R. & Baverel, O. Pseudo-geodesic gridshells. Eng. Struct. 279, 115558. https://doi.org/10.1016/j.engstruct.2022.115558 (2023).
Xu, Y., Gai, Y., Li, H. & Han, Q. Multi-objective shape-section optimization of free-form latticed shells using the RBF-NSGA-II algorithm. Thin-Walled Struct. 200, 111918. https://doi.org/10.1016/j.tws.2024.111918 (2024).
Tomei, V. The effect of joint stiffness on optimization design strategies for gridshells: The role of rigid, semi-rigid and hinged joints. Structures 48, 147–158. https://doi.org/10.1016/j.istruc.2022.12.096 (2023).
Raffaele, L., Bruno, L., Laccone, F., Venuti, F. & Tomei, V. Holistic performance assessment of gridshells: Methodological framework and applications to steel gridshells. J. Build. Eng. 90, 109406. https://doi.org/10.1016/j.jobe.2024.109406 (2024).
Wang, H. & Wu, M. Global shape optimization of free-form cable-stiffened latticed shell based on local optimal solutions. Eng. Struct. 168, 576–588. https://doi.org/10.1016/j.engstruct.2018.05.008 (2018).
Tomei, V., Grande, E. & Imbimbo, M. Design optimization of gridshells equipped with pre-tensioned rods. J. Build. Eng. 52, 104407. https://doi.org/10.1016/j.jobe.2022.104407 (2022).
Yan, J., Qin, F., Cao, Z., Fan, F. & Mo, Y. L. Mechanism of coupled instability of single-layer reticulated domes. Eng. Struct. 114, 158–170. https://doi.org/10.1016/j.engstruct.2016.02.005 (2016).
Gioncu, V. Buckling of reticulated shells: State-of-the-Art. Int. J. Space Struct. 10(1), 1–46. https://doi.org/10.1177/026635119501000101 (1995).
Lenza, P. Non-linear behaviour of reticulated cylindrical vaults. In: Spatial structures at the turn of the millennium, IASS Symp, Copenhagen, vol. 3, p. 143–50 (1991).
Barbieri, N., Machado, R. D., Barbieri, L. S. V., Lima, K. F. & Rossot, D. Dynamic behavior of the geodesic dome joints. Int. J. Comput. Appl. 140(6), 40–44 (2016).
Roopa, M., Hafsa, N. & Venugopal, H. Seismic analysis of a geodesic dome using time history method. Int. Res. J. Eng. Technol. 8(11), 118–121 (2021).
Dede, T., Grzywinski, M. & Selejdak, J. Continuous size optimization of large–scale dome structures with dynamic constraints. Struct. Eng. Mech. 73(4), 397–405. https://doi.org/10.12989/sem.2020.73.4.397 (2020).
Dede, T., Atmaca, B., Grzywinski, M. & Rao, R. V. Optimal design of dome structures with recently developed algorithm: Rao series. Structures 42, 65–79. https://doi.org/10.1016/j.istruc.2022.06.010 (2022).
Bysiec, D. Maleska, T. & Janda, A. Dynamic characteristic of geodesic domes with different location of mass. The Eighth International Symposium on Life-Cycle Civil Engineering IALCCE, Italy (CRC Press, 2023).
Pilarska, D. & Maleska, T. Numerical analysis of steel geodesic dome under seismic excitation. Materials 14(16), 4493. https://doi.org/10.3390/ma14164493 (2021).
Bysiec, D. & Maleska, T. Influence of the mesh structure of geodesic domes on their seismic response in applied directions. Arch. Civ. Eng. https://doi.org/10.24425/ace.2023.146067 (2023).
Pilarska, D. Two subdivision methods based on the regular octahedron for single-and double-layer spherical geodesic domes. Int. J. Space Struct. 35(4), 160–173. https://doi.org/10.1177/0956059920956944 (2020).
Bysiec, D. Sustainable shaping of lightweight structures created according to different methods. Sustainability 15, 3236. https://doi.org/10.3390/su15043236 (2023).
Bysiec, D., Jaszczyński, S. & Maleska, T. Analysis of lightweight structure mesh topology of geodesic domes. Appl. Sci. 14, 132. https://doi.org/10.3390/app14010132 (2024).
Eurocode 3: Design of steel structures
Eurocode 1: Actions on structures
Eurocode: Basis of structural design
Author information
Authors and Affiliations
Contributions
Conceptualization, DB; methodology, DB; software, DB; validation, DB; formal analysis, DB; investigation, DB; writing—original draft preparation, DB; writing—review and editing, DB; visualization, DB.
Corresponding author
Ethics declarations
Competing interests
The author declares no competing interests.
Additional information
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Bysiec, D. Constructions of innovative geodesic domes in terms of the sustainable and efficient cross-sections using. Sci Rep 14, 20444 (2024). https://doi.org/10.1038/s41598-024-71553-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-71553-6