Introduction

Over the years, researchers have investigated different aspects of jet injection phenomena. Even in recent years, in addition to common numerical and experimental studies, due to the complexity of this phenomenon, researchers have used different methods to analyze this phenomenon1,2. Among the many factors, one of the most important ones that affect the jet flow is the geometry of the injector orifice. Non-circular orifices have been among the favorite cases3,4,5. One of the different geometries is high aspect ratio injectors. When the aspect ratio of the orifice of the injector is high (the slit is too narrow), the liquid leaves the injector as a 2-D sheet. In recent decades, using liquid sheets has been practical in many industries. The water spray curtain is a simple and practical technique to abate various industrial risks6. One of the most efficient techniques in the cooling industry is the liquid film cooling technique, used in multiple engineering domains7,8,9. Optimized liquid film cooling can be achieved by injecting a two-dimensional liquid coolant10,11. The effect of different factors on the disintegration of liquid sheets has been studied frequently12,13,14,15,16,17,18,19. Dombrowski et al. performed brilliant research to investigate the sheet's disintegration and breakup15,16,17. A survey was done on the different methods for generating liquid sheets15. Mansour et al. studied the stability and disintegration of two-dimensional liquid sheets, leaving an air-assisted injector18. They reported that the sheet converged toward the axis without airflow, with a linear increase in convergence length with flow rate. Furthermore, three phenomena have been introduced for the case without airflow: the crisscross patterns owing to the capillary waves emanating from the rims of the sheets, small distortion (ripples) due to transition to turbulence, and the point disturbances. Carvalho et al. checked the disintegration of a 2-D liquid sheet with an aspect ratio of 114, enclosed by two air streams, using an airblast atomizer19. They reported the breakup length and breakup frequency results and mentioned that the liquid sheet breakup is a periodic phenomenon. They also proposed a correlation for the non-dimensional breakup length as a function of air the air-to-liquid momentum ratio. Li and Ashgriz reported two breakup modes for liquid sheets due to the impinging of two jets: capillary and Kelvin–Helmholtz instability modes have been introduced20. In the first mode, capillary instability causes droplet formation from the rim of the sheet, while in the second one, the interaction between the sheet and the ambient air leads to the sheet breaking up. These two modes are categorized into five sorts of regimes based on the characteristics of the sheet. The effect of viscosity on the characteristics of liquid sheets made by splash plate nozzle was investigated21. It was mentioned that the Rayleigh–Plateau and Rayleigh–Taylor instabilities governed the sheet atomization.

The liquid jets in crossflow have frequently been of interest22,23,24,25,26,27,28,29. In the last two decays, the spray sheets in cross flow have been investigated30. Jaberi and Tadjfar experimentally investigated the overall dynamics of 2-D liquid sheet flow in still air and subsonic air crossflow31,32. Three injectors with high aspect ratios of 30, 60, and 90 were used in their research31. Two-dimensional liquid sheet regimes in still air were divided into four categories, which were captured with the help of image photography and shadowgraphy techniques. Four drip, column, triangular, and perforation regimes were proposed. Also, they inquired about the flow dynamics of the liquid sheets in subsonic air crossflow experimentally31,32. The liquid was injected from an injector with a high aspect ratio (a narrow gap of very low thickness). A nouveau structure called an inflated sheet has been found. In addition, the regimes of 2-D liquid sheets in crossflow were classified into five groups: biconvex, enclosed inflated sheet, open inflated sheet, bag breakup/sheet rupture, and multimode breakup. Parameters like breakup coordinates, sheet trajectory, and sheet width were reported. An empirical correlation was suggested to predict the trajectory of the liquid sheet32.

Recently, the effect of injection strategies like the orifice orientation, number of injections, and the angle of injections have been of interest33,34,35,36,37,38. The influence of a number of injections and intake temperature on conical film was inquired experimentally and numerically33. The influence of two perpendicular and aligned orientations of rectangular orifices was surveyed, and experimental correlations in terms of momentum ratio and gas Weber number were presented35. It was mentioned that the orientation of the orifice significantly affected rectangular jet parameters. The effect of the variation of injection angle of the liquid flow emanating from a circular nozzle into air crossflow was experimentally investigated36,37,38. Kasmaiee and Tadjfar, measured several jet flow parameters, like breakup point coordinates and trajectory, for different injection angles. In addition, they developed theoretical models for predicting liquid jet trajectory and its breakup point by taking the effect of injection angle into account36. In the following, Kasmaiee and Tadjfar, developed the theoretical models for surface wavelength and frequency of column waves by considering the effect of injection angle37. Next, Kasmaiee et al. used the linear stability theory to show the influence of the injection angle on the wave growth rate. They obtained the breakup height based on the maximum growth rate38.

This paper presents the effect of slit orientation relative to incoming airflow on the flow dynamics of the 2-D liquid sheet injected from a high aspect ratio nozzle. As far as we are aware, there are no previous work that investigated this issue. One can imagine three possible orientations of liquid sheet injected into a cross flow: aligned, perpendicular, and angled. In the existing literature, only the effect of the aligned and perpendicular cases and only for the rectangular injectors (not high aspect ratio injectors) were investigated34,35. A high aspect ratio nozzle injects a 2-D liquid sheet, that is the ideal case in liquid film cooling. One of the most efficient techniques in the cooling industry is liquid film cooling7,8,9. Optimized liquid film cooling can be achieved by injecting a two-dimensional liquid coolant10,11. The main part of this work focused on the morphology of the liquid sheet at different slit orientations. It has also surveyed the variation of the breakup height due to the change in the angle of the slit orientation. A model was proposed to predict breakup height based on the angle of orientation, momentum ratio, and Gas Weber number. In addition, the sheet trajectory was defined and measured for the test cases. Some correlations were achieved for sheet trajectory at different angles of orientation.

Experimental setup

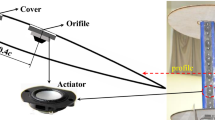
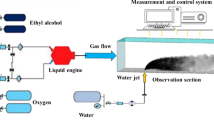
The experimental apparatus's main parts are the wind tunnel, liquid injection system, and high-speed photography unit. The schematic of this setup is illustrated in Fig. 1. A high-pressure nitrogen capsule was used to apply pressure to the tap water stored in a 70-L tank. The advantage of N2 gas is that it reduces the unpleasant vibrations of pumping. A buffer inside the tank intercepted mixing gas with liquid. A rotameter-type flowmeter with an approximate accuracy of about ± 0.15 L/h was armed with a needle valve to measure and adjust the flow rate31,32,39. The needle valve regulated the flow rates of the liquid. The port size of the needle valve is 18 mm. Then, the liquid was directed to the injector through a pipe. The tests were executed in an open-circuit wind tunnel with airspeed up to 45 m/s. The motor used in the wind tunnel is a blower fan that conducts the environment air towards the settling chamber of the tunnel. After the settling chamber, the air passes the contraction zone and enters the test section. The dimension of the rectangular cross-section of the test section is 300 * 300 mm, and its length is 1300 mm. In order to control the speed of the air, an inverter was used to adjust the operation frequency of the tunnel motor. A conversion card connected the inverter to the computer to adjust the motor frequency online by the user31,32.

Fig. 1
figure 1

The experimental setup schematic.

Full size image

An injector with a narrow slit of a high aspect ratio was used, so the injected liquid had the form of a wide two-dimensional sheet with very little thickness. The injector slit width and thickness were 31.5 and 0.35 mm, respectively. The general schematic of the high aspect ratio injector and its two views are exhibited in, Fig. 2a–c, respectively. Liquid enters the input section of the settling chamber, flows towards the outlet, and leaves through the high aspect ratio slit (31.5 mm width and 0.35 mm thickness), forming a 2-D liquid sheet.

Fig. 2
figure 2

Geometry details of injector, (a) total plan of injector, (b) cross section A–A, (c) cross section B-B, (d) injector picture and 3-D isometric view.

Full size image

To visualize the flow physics of the two-dimensional liquid sheets emerging out into the transverse airflow diffused backlight shadowgraph technique was used. In this regard, two high-lumen LEDs as a light source located in the back of the subject (liquid sheet flow) and a camera placed in front of the subject were utilized to capture the shadow of the subject (injected liquid sheet). Due to change in density, refractive index of light varies and the rays are deflected. The result is that the rays join each other on the camera screen and create bright and dark spots (shadows). Therefore, owing to the noticeable density gradient in the liquid–gas two-phase flows, this method is very effective. A homogeneous light was produced with the high-lumen LED lights and a diffuser soft box31,32,39. Snapshots were captured with a Nikon1 J4 digital camera fitted with a Macro-Nikkor AF-S 60 mm f/2.8 G lens. The camera can capture images with frame rates of 60 fps, 120 fps, 400 fps, and 1200 fps. For the mentioned frame rates, the resolutions are 5322 × 3488, 1280 × 720, 768 × 288 and 416 × 144 respectively. The high resolution improves the images' quality and captures even the small phenomena. The minimum exposure time of the tests is 62.5 \(\mu s\). This time is short enough to capture most of the phenomena of the injected liquid sheet31,32,39.

Flow conditions

As a means to investigate the effect of the slit orientation relative to the subsonic crossflow of air, a wide range of flow conditions was made in the experiments. The intended working fluid was water with a temperature of room (T = \({25}^{^\circ }\) ~ \({30}^{^\circ }\)), density of \({\rho }_{l}= 995 kg/m3\), and surface tension of \(\sigma = 0.0728 N/m\). Also, the air density was \({\rho }_{g}= 1.225 kg/m3\). Concerning liquid sheets injected into a gaseous crossflow, the non-dimensional parameters are liquid-to-gas momentum ratio, gas Weber number, and liquid Weber number, which have played important roles in characterizing the flow dynamics. The definitions of these parameters are respectively as follows:

$$q=\frac{{\rho }_{s}{V}_{s}^{2}}{{\rho }_{g}{V}_{g}^{2}}$$
(1)
$${We }_{s}=\frac{{\rho }_{l}{V}_{s}^{2}{t}_{H}}{\sigma }$$
(2)
$${We }_{g}=\frac{{\rho }_{g}{V}_{g}^{2}{t}_{H}}{\sigma }$$
(3)

where \({V}_{s}\) and \({V}_{g}\) are the liquid sheet velocity and airflow speed, respectively, and \({t}_{H}\) and is the sheet thickness. The physical properties of water and air are given in Table 1.

Table 1 Physical properties of water and air.
Full size table

The direction of the slit orientation of the injector could change relative to the airflow. When the angle of orientation is 0, it means that the slit is aligned with the airflow direction. So, the airflow direction influences the windward side of a 2-D liquid sheet. When the angle of orientation is 90, the slit is perpendicular to the airflow direction, which means that the width of the liquid sheet is affected by air equally and simultaneously. When the slit is at an angle between 0 and 90, its orientation is crooked relative to the airflow direction based on the defined angle. Therefore, some parts of the liquid sheet are more affected by the air and contrary some are less affected. The orientation of the injector relative to airflow is exhibited in Fig. 3.

Fig. 3
figure 3

Shematic of orientation of injector slit relative to the airflow.

Full size image

Image processing

Figure 4 depicts the image processing method used to track the trajectory of a 2-D liquid sheet. This technique was used and validated by previous research32. A high-speed camera captured grayscale images of liquid sheets. For the first step, these images were changed to binary images. In this work, the adaptive threshold method has been used to make binary images36. Since the behavior of liquid sheets in crossflow was so unpredictable, the trajectory was determined from an accumulation of all binary images instead of a single image in the next step. Finally, again, the adaptive threshold method acted on the result of binary images accumulation. In this step, the number of pixels of the outlet injector section transformed to the physical diameter of 55 mm, so the distance of points on the trajectory identified by pixels could be converted to a length unit of mm.

Fig. 4
figure 4

The image processing method to track trajectory.

Full size image

Flow morphology

The effect of injector orientation relative to the cross-flow on the liquid sheet morphology is investigated. The surface tension and inertia force rule the dominant phenomenon for a sheet in still air31. For a constant momentum ratio, at a very low liquid Weber numbers of the range of this study, as soon as the liquid emanates from the injector, the surface tension acts powerfully, and the liquid changes to a column. Here, the aerodynamic and inertia forces were trivial compared to surface tension. As the sheet Weber number became higher, the role of inertia force became more prominent, and the liquid could leave the slit as a sheet with a cross-section equal to the slit cross-section. The surface tension acted on the edges of the sheet in the boundaries of liquid and air, and the rims were born and became thicker downstream until they coalesced at the central axis of the sheet. So, the liquid sheet had the form of a triangle and has been named the triangular sheet31,32. The point of convergence was called the convergence point, and the distance from the nozzle exit to the convergence point was called the convergence length, which has been measured in previous research31. After the converging point, another sheet was formed due to the impact of the rims. It could be considered like the sheet formed by the impinging of laminar jets. The Rims acted like jets. Thus, another sheet with a perpendicular axis to the first sheet was formed. This sheet has been called the biconvex structure. After that, the two rims coalesced into a column influenced by the inertial-capillary interaction. As a result, the Plateau-Rayleigh type of instability led to the breakup at the end of the column. In the aligned case (\(\theta \) = 0), the sheet structures exposed to the traverse airflow at low liquid Weber numbers were like the sheet in stagnant air. The difference is that they were influenced by the aerodynamic force and bent in the air direction. The flow development of liquid sheets in low-speed air can be seen in Fig. 5a–c.

Fig. 5
figure 5

Flow development of liquid sheet for the case \(\theta \) = 0 at the constant momentum ratio of q = 67, (a) \({We}_{s}\) = 1.22, \({We}_{g}\) = 0.018, (b) \({We}_{s}\) = 2.73, \({We}_{g}\) = 0.041, (c) \({We}_{s}\) = 9.52, \({We}_{g}\) = 0.142.

Full size image

By increasing the air speed, the effect of aerodynamic force became more. In addition to the aerodynamic force, the orientation of liquid sheet relative to the airflow direction held attention, which would be discussed as follows.

Slit orientation relative to the airflow

Aligned slit

In the case that the injector slit was aligned with the airflow direction (\(\theta \) = 0), as the liquid leaved the injector, the windward side was affected by air force. At low sheet Weber number, as mentioned above, the structure was like the liquid sheet in the stagnant air31. Since the velocity of rims was low, the sheet produced due to the impact of the rims was stable and was similar to pre-sheet formation sub-regime of capillary instability regime20. This could be seen in Fig. 6.

Fig. 6
figure 6

Sheet formed after the impact of rims at \(\theta \) = 0, \({We}_{s}\) = 9.52, \({We}_{g}\) = 0.1, q = 100.

Full size image

As it is exhibited in Fig. 7, at constant sheet Weber number, when the air velocity increased, the second sheet was similar to the smooth sheet sub-regime of capillary instability regime20. The angles between rims and the injection velocities for two cases (Fig. 7a,b) were the same, so the aerodynamic force governed the change of the sub-regimes of the sheets. In Fig. 7b the bead-like shapes and ligaments attached to the sheet are seen.

Fig. 7
figure 7

Sheet structures at \(\theta = 0^\circ \), (a) \({We}_{s}\) = 9.52, \({We}_{g}\) = 0.1, q = 100, (b) \({We}_{s}\) = 9.52, \({We}_{g}\) = 0.32, q = 30.

Full size image

When the liquid sheet was aligned with the airflow, the triangular sheet was maintained; as the gas Weber number increased for the case of constant momentum ratio, it is obvious in Fig. 8a that the air could rotate this second sheet. Following the increase of gas Weber number (Fig. 8b), as the airflow penetrated the bottom sheet, the bags formed, and the break up happened. At high Weber number (Fig. 8c), sometimes, due to the increase in airspeed, the second sheet only remained for a very short period of time. The Sheet rupture happened quickly, and it expanded. Due to the surface tension, the rupture went towards the rims. Also, the rims broke down very quickly. Also, there were multiple bag breakups on the second sheet. At such a high Weber number, the perforation was born on the triangular sheet and started to grow in the direction of liquid stream movement.

Fig. 8
figure 8

Sheet structures flow structure at constant momentum ratio of 30, (a) \({We}_{s}\) = 9.52, \({We}_{g}\) = 0.32, (b) \({We}_{s}\) = 15.74, \({We}_{g}\) =0.54, (c) \({We}_{s}\) = 23.51, \({We}_{g}\) = 0.78,

Full size image

Perpendicular slit

When the injector slit was perpendicular to the airflow, the liquid sheet was symmetrical relative to the axis of the air direction. Indeed, the regimes of the two-dimensional liquid sheet were categorized into the biconvex, enclosed inflated sheet, open inflated sheet, bag breakup/sheet rupture, and multimode breakup32. The structures of liquid sheet injected orthogonal to the airflow (\(\theta \) = 90) are exhibited in Fig. 9. At low Weber numbers, after the convergence point, the biconvex structure is obvious (Fig. 9a). Indeed, the aerodynamic force was not potent enough to influence the biconvex structure; besides, the liquid sheet was disintegrated owing to the Plateau-Rayleigh instability. As the airflow increased gradually, the biconvex structure disappeared. As the increase of air Weber's number continued, the air penetrated the sheet between rims and stretched the sheet in its direction. The sheet had a puffed structure (Fig. 9b); it was named an inflated sheet31,32. Firstly, the rims coalesced downstream and made a column, so the inflated sheet was enclosed. By increasing the air velocity, the enclosed sheet expanded (Fig. 9c) until the column of rims disappeared. During this process, the sheet thickness decreased, leading to the sheet rupture at the end, and the open inflated sheet was born (Fig. 9d). By increasing the air velocity more, the bags formed on the sheet, and in addition to the sheet rupture, there were bag breakup (Fig. 9e).

Fig. 9
figure 9

Flow structure of the two-dimensional liquid sheet at \(\theta \) = 90 and constant momentum ratio of 100, (a)\({We}_{s}\) = 4.86, \({We}_{g}\) = 0.05, q = 100, (b) \({We}_{s}\) = 12.44, \({We}_{g}\) = 0.12, (c) \({We}_{s}\) = 19.4, \({We}_{g}\) = 0.19, (d) \({We}_{s}\) = 32.8, \({We}_{g}\) = 0.33, (e) \({We}_{s}\) = 49.8, \({We}_{g}\) = 0.5.

Full size image

Angled slit

By changing the orientation from zero degrees to other states, unlike the aligned case, the left rim (the further rim) of the sheet, as the liquid left the injector, was influenced by the wind flow. The two rims got close to each other owing to the surface tension force, but they did not collide to make a triangular sheet. Also, the biconvex structure was not formed at low Weber numbers in the test. Instead, at low Weber numbers, the enclosed inflated sheet started to form (Fig. 10a). Like the case \(\theta \) = 0, the left rim (further rim) moved to the right direction, and the right rim (closer rim which is affected by air flow sooner) acted as the case \(\theta \) = 90 and moved to the air direction. So, the two rims' behavior was not symmetrical like the perpendicular case (\(\theta \) = 90), and there was an asymmetry between the two parts of the liquid sheets. Unlike the case \(\theta \) = 90, since the liquid sheet orientation was not orthogonal to the air direction, the amount and speed of bending of the sheet parts were not the same. The right rim and the part of the sheet attached to it bent faster in the airflow direction. It can be interpreted as the moments of air force about the center point of the slit on the two sides of the sheet were not equal. The moment of the air force exerted on the right rim became more than the moment of the air force on the left rim, leading to the twist of the sheet around the center axis. This resulted in the reduction of breakup height in comparison to aligned and perpendicular cases. The change of flow structure of \(\theta \) = 60 at a constant momentum ratio of 100 is represented in Fig. 10. Figure 10b shows an expanded enclosed inflated sheet, while this structure could be seen in higher gas Weber numbers in Fig. 10c for the case \(\theta \) = 90. Also, an open inflated sheet existed at a lower gas Weber number at \(\theta \) = 60 (Fig. 10c) compared to the case \(\theta \) = 90. At higher Weber numbers, there was an extended open inflated sheet, and sheet rupture happened (Fig. 10d). When the air velocity became higher, the bags were born on the sheet, and the breakup regime was bag breakup/sheet rupture (Fig. 10e).

Fig. 10
figure 10

Flow structure of the Flow structure of the two-dimensional liquid sheet at \(\theta \) =60 and constant momentum ratio of 100, (a)\({We}_{s}\) = 4.86, \({We}_{g}\) = 0.05, q = 100, (b) \({We}_{s}\) = 15.74, \({We}_{g}\) = 0.16, (c) \({We}_{s}\) = 19.4, \({We}_{g}\) = 0.19, (d) \({We}_{s}\) = 32.8, \({We}_{g}\) = 0.33, (e) \({We}_{s}\) = 49.8, \({We}_{g}\) = 0.5

Full size image

Results and discussion

The results are presented and discussed in the current section.

Breakup height

The breakup of liquid sheets is one of the main parameters that impact atomization characteristics. The breakup height is defined as the distance between the injector output orifice and the horizontal plane where the film breakup first occurs. In Fig. 11, the breakup height is marked with \({Z}_{b}\).

Fig. 11
figure 11

Definition of breakup height, \(\theta \) = 30, \({We}_{s}\) = 9.52, \({We}_{g}\) = 0.1, q = 100.

Full size image

Historically, the effect of orifice orientation on the breakup phenomenon cannot be ignored34,35.

Mechanism of breakup

In this assay, by changing the orientation from zero degrees to other states, the other edge of the sheet was influenced by the wind flow and started bending in the direction of the airflow. The breakup height was reduced because of the asymmetry and the twist of the sheet. Also, the frontal area of the sheet increased with the increase of the orientation angle, leading to an increase in the drag force and a reduction in the breakup height. Indeed, the effect of the increase of frontal area (drag force) and penetration of the air into the sheet became greater. As a result, the breakup height decreased, and the sheet bent more in the airflow direction. Beyond the orientation angle of \(\theta ={45}^{^\circ }\), the difference between the moments of air forces of two sides of the liquid sheet became less and less. Therefore, there was more symmetry about the central line of the sheet. Thus, the breakup height increased despite the increase in the frontal area. Indeed, the effect of the drag force was less than the symmetry of the sheet. So, the variation of breakup height with the angle of orientation had a polynomial behavior. The change of breakup height for different orientation angles is illustrated in Fig. 12. As mentioned, in all cases a polynomial behavior can approximately be seen. As it is obvious, at low gas and sheet Weber numbers the rate of the variation of breakup height is high (e.g., Fig. 12a: \({\text{We}}_{\text{s}}\) = 9.52, q = 60, \({We}_{g}=0.16\), Fig. 12b: \({\text{We}}_{\text{s}}\) = 15.74, q = 100, \({We}_{g}=0.16 )\)). As it would be discussed next, the main reason for the different behavior in this cases is the change in the regime of the liquid sheet structure. As the sheet and gas Weber number increased, the rate of the change of the breakup height with angle of orientation became less and the trend of the breakup height changes for all momentum ratios became similar (e.g., Fig. 12c).

Fig. 12
figure 12

Effect of the momentum ratio on sheet-wise breakup of the two-dimensional liquid sheet in crossflow in different orientations of liquid sheet, (a) \({We}_{s}\) = 9.52, (b) \({We}_{s}\) = 15.74, (c) \({We}_{s}\) =23.51.

Full size image

In Fig. 13, at low gas Weber number of \({We}_{g}\) = 0.16, sheet Weber number of \({\text{We}}_{\text{s}}\) = 15.74, and momentum ratio of q = 100, the breakup height is compared in different liquid sheet orientations. As it is mentioned previously, the sheet regimes changed by variation of angle of orientation. From \(\theta ={20}^{^\circ }\) to \(\theta ={45}^{^\circ }\) the breakup regime is open inflated sheet. At \(={60}^{^\circ }\) , \(\theta ={75}^{^\circ }\), and \(\theta ={90}^{^\circ }\), the sheet regime is the enclosed inflated sheet that ends with a column, and the breakup regime is like the column breakup regime. Since the frontal area of the liquid sheet increased with the angle of orientation (from \(\theta ={0}^{^\circ }\) to \(\theta ={45}^{^\circ }\)), the effect of aerodynamic drags grew. Accordingly, the breakup height decreased. Beyond \(\theta ={45}^{^\circ }\), the regime changed and by the increase of the orientation angle up to \(\theta ={90}^{^\circ }\), the symmetry of the sheet relative to the crossflow augmented. As a result a severe increase in breakup height could be seen. At higher air velocities, the slope of the variation of the breakup height with the angle of orientation became less. So, the rate of change of the breakup height between different orientations decreased (e.g., Fig. 12c).

Fig. 13
figure 13

change of breakup regime, \({We}_{s}\) = 15.74, \({We}_{g}\) = 0.16, q = 100.

Full size image

In Fig. 14, the gas Weber number increased to \({We}_{g}\) = 0.39 (\({We}_{s}\) =23.51, q = 60). At \(\theta ={0}^{^\circ }\) (Fig. 14a), the rims converged and made a triangular sheet. After that, a small sheet was formed due to rim impingement. From \(\theta ={20}^{^\circ }\) to \(\theta ={90}^{^\circ }\) (Fig. 14b–g), the structures were the open inflated sheets, and the sheet rupture happened. In all of them, a multi-mode breakup regime governed the breakup phenomenon. Since the structures from \(\theta ={20}^{^\circ }\) to \(\theta ={90}^{^\circ }\) were the same, the slop of variation of breakup height was lower, and from \(\theta ={45}^{^\circ }\) to \(\theta ={90}^{^\circ }\), there was a slight increase in breakup height owing to the increase of sheet symmetry relative to the air direction.

Fig. 14
figure 14

Flow structure of the different orientations of two-dimensional liquid sheet at the constant momentum ratio of 60,\({We}_{s}\) = 23.51, \({We}_{g}\) = 0.39, (a) \(\theta \) = 0, (b) \(\theta \) = 20, (c) \(\theta \) = 30, (d) \(\theta \) = 45, (e) \(\theta \) = 60, (f) \(\theta \) = 75, (g) \(\theta \) = 90.

Full size image

Model for breakup height

A model for predicting the breakup height for this study was achieved from the time scale presented by Clark40. The breakup point is the distance from the injector orifice to the fracture point in the x and z direction. Wu et al. proposed a model for the breakup height of liquid jets in crossflow22. As mentioned22,40, the time scale for the fracture of the liquid jet column in crossflow is obtained from the completion of the secondary breakup. So, the breakup time for a liquid column can be considered as:

$${t}_{b}= {c}_{t}\sqrt{\left(\frac{{\rho }_{l}}{{\rho }_{g}}\right)}/{u}_{g}$$
(4)

where \({c}_{t}\) is a constant and could be defined as a function of frontal length as below39:

$${c}_{t}=n{D}_{f}/{c}_{D}$$
(5)

where \({c}_{D}\) is the drag coefficient, \(n\) is a constant, and \({D}_{f}\) is a frontal length to the airflow40. The element of the liquid sheet exposed to the crossflow is rectangular. The larger dimension of it is equal to the width of the injector slit, and its smaller dimension is equal to the sheet thickness. So, the frontal length for this study is equal to:

$${D}_{f} =\left(w \text{cos}\theta + {t}_{H} \text{sin}\theta\right)$$
(6)

\(w\) is the width of the sheet and \({t}_{H}\) is the sheet thickness. Replacing the above equation in Eq. (5) yields:

$${C}_{t}=n\left(w \text{cos}\theta + {t}_{H} \text{sin}\theta\right)/{c}_{D}$$
(7)

For a rectangular element as a plate in crossflow, the pressure drag coefficient depends on crossflow Reynolds number41 and is related as follows:

$${c}_{D} \propto {1}/{{Re}_{g}}$$
(8)

where the crossflow Reynolds number is defined on the base of frontal dimension:

$${Re}_{g}= \rho {u}_{g}{D}_{f}/{\mu }_{g}$$
(9)

where \({u}_{g}\) is the crossflow velocity. Replacing the Eq. (8) and Eq. (9) in Eq. (5), the below result obtained:

$${C}_{t}\propto {{D}_{f}}^{2}$$
(10)

By inserting Eq. (6) in Eq. (10),

$${C}_{t}\propto { \left(w\text{sin}\theta+{t}_{H}\text{cos}\theta\right)}^{2}$$
(11)

According to the work of Wu et al.22, the injection velocity does not change along the jet column up to the breakup point. So, the sheet-wise breakup height \({Z}_{b}\) can be achieved by multiplying the breakup time \({t}_{b}\) by constant injection velocity \({u}_{j}\) as follows:

$${Z}_{b}={C}_{t} \frac{{u}_{j}}{{u}_{g}}\sqrt{\left(\frac{{\rho }_{l}}{{\rho }_{g}}\right)}$$
(12)

The non-dimensional breakup height is defined by dividing the breakup height by sheet thickness \({t}_{H}\):

$$\frac{{Z}_{b}}{{t}_{H}}=\frac{{C}_{t}}{{t}_{H}} \frac{{u}_{j}}{{u}_{g}}\sqrt{\left(\frac{{\rho }_{l}}{{\rho }_{g}}\right)}$$
(13)

Replacing the \({C}_{t}\) from Eq. (11), in above equation leads:

$${{Z}_{b}}/{{t}_{H}} \propto { \left(AR \text{sin}\theta+ \text{cos}\theta\right)}^{2} \sqrt{q}$$
(14)

where \(AR = {w}/{{t}_{H}}\) is the aspect ratio of the injector orifice and \(\frac{{u}_{j}}{{u}_{g}}\sqrt{\left(\frac{{\rho }_{l}}{{\rho }_{g}}\right)}\) is replaced by q as the momentum ratio.

Equation (14) could be written as:

$${{Z}_{b}}/{{t}_{H}} = {c}_{1} {q}^{{c}_{2}}$$
(15)

Based on the significant effect of the gas Weber number on breakup height, the gas Weber number was added to the above equation according to the previous research of Ragucci et al.42. So, Eq. (15) for breakup height is as below:

$${{Z}_{b}}/{{t}_{H}} = {c}_{1} {q}^{{c}_{2}}{{we}_{g}}^{{c}_{3}}$$
(16)

The coefficients \({c}_{2}\) and \({c}_{3}\) were achieved by the curve fitting the experiment measurements.

$${{Z}_{b}}/{{t}_{H}} = {c}_{1} {q}^{0.51}{{we}_{g}}^{-0.18}$$
(17)

By comparing the Eqs. (16) and (14), it was assumed that, \({c}_{1}\) is a function of the slit angle of orientation \(\theta\):

$${c}_{1}=f( \left(AR \text{sin}\theta+ \text{cos}\theta\right))$$
(18)

where \(R \text{sin}\theta+ \text{cos}\theta\) , is named S as a new non-dimensional parameter that illustrates the effect of slit orientation angle:

$$S= AR \text{sin}\theta+ \text{cos}\theta$$
(19)

So, it could be stated that \({c}_{1}\) is a function of the parameter S. It was absolutely obvious from the experiment data that the changes of \({c}_{1}\) relative to the non-dimensional parameter S is a kind of polynomial shape.

$${c}_{1} = 0.0041 {\left(AR \text{sin}\theta+ \text{cos}\theta\right)}^{2}-0.4228\left(AR \text{sin}\theta+ \text{cos}\theta\right)+27.71$$
(20)

This is illustrated in Fig. 14a. The coefficient of determination (\({R}^{2}\)) equals to 0.94, which is defined as:

$${R}^{2}=1-\frac{SSE}{SST}$$
(21)

where:

$$SSE=\sum_{i=1}^{n}{({y}_{i}-{\widehat{y}}_{i})}^{2}$$
(22)
$$SST=\sum_{i=1}^{n}{({y}_{i}-\overline{y })}^{2}$$
(23)

where, \({y}_{i}\) is the main data, and \({\widehat{y}}_{i}\) is the predicted data by the model, and \(\overline{y }\) is the mean of the main data. The final formula of the proposed model could be:

$${{Z}_{b}}/{{t}_{H}} = ( 0.0041 {\left(AR\text{ sin}\theta+\text{ cos}\theta\right)}^{2}-0.4228\left(AR\text{ sin}\theta+\text{ cos}\theta\right) +27.71) {q}^{0.51}{{we}_{g}}^{-0.18}$$
(24)

The polynomial behavior of the coefficient \({c}_{1}\), in Fig. 15, is in good agreement with the Eq. (14)

Fig. 15
figure 15

Curve fit of variation of \({c}_{1}\) with non- dimensional parameter S.

Full size image

The comparison between Present measurements and the predicted values of the above model is shown in Fig. 16.

Fig. 16
figure 16

Curve fit of variation of \({c}_{1}\) with non- dimensional parameter S.

Full size image

As can be seen in Fig. 16, the evaluated error between each measurement and the corresponding predicted value is less than twenty percent. Therefore, the model has an agreeable accuracy in predicting the sheet breakup height in different orientation angles of the slit. To show proposed model's acceptable accord with the real measurements, the data of three cases are compared with the predicted value of the given model in Fig. 17a–c.

Fig. 17
figure 17

Comparison between achieved model and the experiment measurements at constant momentum ratio of 30, (a), \({We}_{s}\) =9.52, \({We}_{g}\) =0.32, (b) \({We}_{s}\) =15.74, \({We}_{g}\) =0.52 (c) \({We}_{s}\) =23.51, \({We}_{g}\) =0.78.

Full size image

Sheet trajectory

In order to achieve an effective understanding of liquid sheet behavior in crossflow for industrial and scientific fields, it is crucial to determine the direction of the bulk of liquid flow. In this regard, the trajectory of the injected liquid sheet into the crossflow plays a pivotal role in determining the amount and direction of penetration of the bulk of liquid in the gas. Because the sheet is not symmetrical relative to the crossflow direction, its different parts do not move in the same path. For this research, the path of the rim which is affected by air flow sooner, was considered as the trajectory. The right rim is more affected by the crossflow. So, the right rim's trajectory is considered to represent the sheet's trajectory. The x-direction aligns with the airflow, while the z-direction is perpendicular to it. Figure 18 provides a clear depiction of the defined trajectory.

Fig. 18
figure 18

Comparison Defined trajectory of the liquid sheet leaving the oriented slit relative to the airflow, \(\theta =45^\circ \), q = 100, \({We}_{s}\) =23.51, \({We}_{g}\) =0.23.

Full size image

One main parameter that impacts the sheet trajectory is the liquid-to-air momentum ratio. So, the impact of the momentum ratio on the defined trajectory at some angles of orientation is given in Fig. 19. The momentum ratio decreased by increasing the airflow speed at a constant sheet Weber number. As a foregone result, for all cases, the trajectory bent more in the airflow direction by reduction of the liquid-to-air momentum ratio, and its penetration into the airflow increased.

Fig. 19
figure 19

the impact of liquid to air momentum ratio on the sheet trajectory at constant sheet Weber number of 23.51 at orientation angles of (a) \(\theta =0^\circ \), (b) \(\theta =30^\circ \), (c) \(\theta =90^\circ \)

Full size image

As depicted in Fig. 19a, the trajectory had three sections for the aligned case. In the first section, which belonged to the triangular sheet, the rate of change of trajectory slope was slight. After that, there was a deflection point. So, the curvature direction changed, and the second short trajectory path continued toward the second deflection point. Then, the trajectory belonged to the second sheet of the aligned structure. For the angle of orientation of \(\theta =30^\circ \), compared with the aligned case, for each momentum ratio, the measured trajectory bent more in the airflow direction, and the slope of the trajectory curves reduced (Fig. 19b). After \(\theta =30^\circ \), by increasing the orientation angle up to \(\theta =90^\circ \), the trend of changes was inversed. The slope of curves was amplified, and the amount of trajectory bending in the airflow direction was reduced (Fig. 19c). This trend is also illustrated in Fig. 20, which shows the trajectory of the orientation angles compared with each other. From Fig. 20, the following observations were made regarding the sheet orientation relative to the crossflow. As mentioned, in all cases, when the sheet orientation changed from being aligned to the angled case \(\theta =30^\circ \), the trajectory bent more in the air direction, and the curve slope reduced. In the aligned case, the slope near the orifice (first section of trajectory) had less difference with the angled cases compared to the further section from the orifice (third section of the aligned case trajectory). Then, by increasing the orientation angle from \(\theta =30^\circ \) to \(\theta =90^\circ \), the trajectory curve slope was augmented, or in other words, the bending amount of trajectory in the airflow direction was reduced.

Fig. 20
figure 20

Trajectories at different orientation of the orifice injectors to the crossflow at \({We}_{s}\) =15.74, (a) \({We}_{g}\) = 0.16, q = 100, (b) \({We}_{g}\) = 0.26, q = 60, (c) \({We}_{g}\) = 0.52, q = 30.

Full size image

By referring to Fig. 20, it can be seen that when the gas Weber number is low (at a momentum ratio of q = 100), the influence of the inertial force surpasses that of the aerodynamic force. The aerodynamic force is comparatively feeble, which results in the sheet moving vertically instead of following the airflow direction (Fig. 20a). However, as the gas Weber number increased while maintaining a constant sheet Weber number of 15.74, the amount of vertical penetration decreased. There is a bifurcation of the trajectories. The trajectories of the angles of orientation from \(\theta =30^\circ \) to \(\theta =60^\circ \) included in one branch and the trajectories of the angles of orientation \(\theta =75^\circ \) and \(\theta =90^\circ \) were in the other branch. The trajectory of the aligned case at a close distance from the injector slit was in the first branch, and after the inflection point, it was included in the second branch. By increasing the Gas weber number or in other words decreasing the momentum ratio, the bifurcation amplified, and the trajectories in the second branch went toward the first branch (Fig. 20b,c).

Correlations for trajectory

In the past, formulas had been developed to establish a correlation between the trajectory of liquid jets in crossflow and the momentum ratio43. For the sheet trajectory, Jaberi and Tadjfar proposed a correlation showing the momentum ratio's effect on the trajectory32:

$${z}/{{t}_{H}} = 11.37 ({{x}/{{t}_{H}})}^{0.241}{q}^{0.414}$$
(25)

However, the significant influence of the gas Weber number on the trajectory could not be ignored35,36. So, for this research, the correlations in the form of a power model were suggested, which related the momentum ratio (q), gas Weber number, and the airflow coordinate (x) at each orientation. angle

$${z}/{{t}_{H}} = {C}_{1}({{x}/{{t}_{H}})}^{{C}_{2}}{q}^{{C}_{3}}{{we}_{g}}^{{C}_{4}}$$
(26)

The results are available in Table 2.

Table 2 Correlations of trajectory.
Full size table

As it is obvious from the correlations of Table 2, the rate of the effect of momentum ratio on the sheet trajectory has been changed significantly by the variation of slit orientation. For example, from the aligned case to the angled case \(\theta =30^\circ \), the increase of the power value of the momentum ratio was about 19 percent, which means the increase of influence of the momentum ratio was about 19 percent on the sheet trajectory. The rate of the effect of gas Weber number with the change of orientation angle is also meaningful. The slope of the sheet trajectory curves is represented by the constant of the equations and power of the stream-wise coordinate x. By variation of angles of orientation, the rate of the slope changes is obvious from the achieved correlations. In conclusion, by changing the angle of the slit orientation, the influence of classical parameters like momentum ratio and gas Weber number on the sheet trajectory could vary significantly.

Conclusions

In this study, for the first time, the effect of variation of the orientation angle of the slit of very high aspect ratio injector relative to the crossflow was investigated. We also showed the influence of the orientation angle on breakup height and sheet trajectory for all three possible orientations: aligned, perpendicular, and angled cases. The flow pictures were taken with a high-speed digital camera, and the shadowgraphy technique was used to show the structures of the flow. The morphology of the sheet in each orientation angle was investigated. As mentioned, the variation in air penetration into the sheet affected the sheet morphology. The change of orientation angle resulted in a change in frontal length and the asymmetry of the sheet relative to the airflow. Due to the asymmetry of the liquid sheet relative to the airflow, in some test conditions, the regime of liquid sheets was different in comparison with perpendicular case.

A polynomial behavior for the variation of breakup height was observed when the slit orientation was changing. Indeed, in addition to the standard flow parameters: gas Weber number and liquid-to-gas momentum ratio, it was found that the frontal area and the asymmetry relative to the crossflow influenced the breakup height. By considering the orientation angle, a new model was proposed to predict the breakup height which was in good agreement with the experiment data. The given model was based on the time scale of breakup presented by Clark et al.40 and the theory of Wu et al.22. The proposed model considered the effect of the orientation angle in addition to the standard parameters of liquid momentum ratio and gas Weber number.

Also, the trace of the orientation angle on the sheet trajectory was investigated. For liquid sheets in an angled orientation relative to the airflow, all of the sheet segments did not bend similarly in the airflow direction. Therefore, the path of the right rim in the images was defined as the trajectory. The defined trajectory was measured for all the test conditions, and the results were compared. The empirical correlations for the sheet trajectory based on the liquid-to-air momentum ratio and gas Weber number at each orientation angle were found and presented. The correlations showed the significant effect of slit orientation on the dependence of sheet trajectory on the liquid-to-air momentum ratio and gas Weber number.