Introduction

Dynamic systems1,2,3,4,5,6,7,8,9,10,11,12,13 are typically used to describe the evolution of a point in geometric space over time. It is a complex interdisciplinary theoretical system that involves multiple fields such as mathematics, physics, transportation, aerospace, and engineering technology. The study of dynamic system theory provides important mathematical models and solutions for solving many practical problems. The study of dynamical systems originated from the study of ordinary differential equations(ODEs). As early as 1881, French mathematician Paincaré founded the study of qualitative theory of ODEs, and introduced the concepts of bifurcation theory and singularities. He introduced the concept of phase space and represented the solution of ODEs as curves in phase space without solving ODEs. Thus, the properties of solutions to ODEs can be studied intuitively. In 1892, Russian mathematician Lyapunov systematically studied the stability of differential equations in his doctoral thesis, and proposed the famous Lyapunov stability theory14. The main characteristic of the qualitative theory of differential equations and Lyapunov stability theory mentioned above is that without solving the equations. After more than a century of rapid development, the qualitative theoretical theory of differential equations has penetrated into many important disciplines. In fact, when the parameters of the system change and pass a certain critical value, the global behavior of the system will suddenly change, which is usually referred to as bifurcation phenomenon. In nature, bifurcation is a common natural phenomenon. In recent years, with the rapid development of science and technology, the theory of dynamic system has become a very powerful mathematical tool. In recent years, Professor Li15,16,,16 has proposed the “three-step method” to study the branches and dynamic properties of traveling wave solutions for nonlinear partial differential equations (NLPDEs)17,18,19 by using qualitative theory of dynamical systems, and the traveling wave solution of NLPDEs are constructed. On the one hand, Professor Li Jibin’s “three-step method” provides a very important solution method for solving traveling wave solutions20,21,22,23,24 of NLPDEs, Through this method, many traveling wave solutions of NLPDEs can be obtained. On the other hand, dynamic system analysis theory can be used to obtain some dynamic characteristics of NPLDEs without solving NLPDEs. However, research on the dynamic behavior of NLPDEs with fractional derivatives25 and the construction of traveling wave solutions are still in their early stages. In this paper, the main purpose of this article is to analyze the bifurcation, chaotic behaviors, and solitary wave solutions of the fractional Twin-Core couplers with Kerr law non-linearity by using the planar dynamical system method.

The fractional Twin-Core couplers with Kerr law non-linearity is described as follows26

$$\begin{aligned} {\left\{ \begin{array}{ll} i^{A}_{0}D_{t}^{\beta }u+\alpha _{1}{^{A}_{0}D_{xx}^{\beta }u}+F(|u|^{2})u=l_{1}{^{A}_{0}D_{xx}^{\beta }(|u|^{2})u}+m_{1}(|u|^{2}){^{A}_{0}D_{xx}^{\beta }u}+g_{1}u^{2}{^{A}_{0}D_{xx}^{\beta }u^{*}}+k_{1}v,\\ i^{A}_{0}D_{t}^{\beta }v+\alpha _{2}{^{A}_{0}D_{xx}^{\beta }v}+F(|v|^{2})v=l_{2}{^{A}_{0}D_{xx}^{\beta }(|v|^{2})v}+m_{2}(|v|^{2}){^{A}_{0}D_{xx}^{\beta }v}+g_{2}v^{2}{^{A}_{0}D_{xx}^{\beta }v^{*}}+k_{2}u, \end{array}\right. } \end{aligned}$$
(1)

where \(u=u(x,t)\) and \(v=v(x,t)\) represent the optical problems in two cores, which are the complex-valued functions. \(^{A}_{0}D_{t}^{\beta }\) and \(^{A}_{0}D_{x}^{\beta }\) are the Atangana’s derivatives about the time and space. \(\alpha _{1}\), \(\alpha _{2}\), \(g_{1}\) and \(g_{2}\) stand for the coefficients of the dispersion terms. \(l_{1}\), \(l_{2}\), \(m_{1}\) and \(m_{2}\) are the constants. When \(\beta =1\), Eqs. (1) become an integer-order Twin-Core couplers model27. The Twin-Core couplers has important physical significance and application value in the fields of optics and optical communication. These couplers are typically composed of two parallel and close optical waveguides or “cores” that exchange energy through optical coupling.

The remaining part of this article is arranged as follows: In “Bifurcation and chaotic behaviors” section, the phase portraits and Poincaré sections of two-dimensional dynamical system and its perturbation system are discussed. In “Solitary wave solutions of Eqs. (1)” section, the solitary wave solutions of the fractional Twin-Core couplers with Kerr law non-linearity are constructed. In “Conclusion” section, a brief conclusion is given.

Bifurcation and chaotic behaviors

Preliminary

Definition 2.1

(Atangana’s fractional derivative)28 For \(\beta \in (0,1]\), the Atangana’s fractional derivative of \(f:[0,+\infty )\rightarrow (-\infty ,+\infty )\) is defined as

$$\begin{aligned} _{0}^{A}\mathbb {D}_{t}^{\beta }(f(t))=\lim _{\varepsilon \rightarrow 0}\frac{f\left( t+\varepsilon \left( t+\frac{1}{\Gamma (\beta )}\right) ^{1-\beta }\right) -f(t)}{\varepsilon },\ 0<\beta <1. \end{aligned}$$

The Atangana’s fractional derivative is also known as the beta fractional derivative, which plays a very important role in the study of exact solutions to fractional partial differential equations. In recent years, there have been many literature reports on this work, and its definition, properties and applications can be referred to in the literature29,30,31,32,33.

Mathematical derivation

Firstly, let us the the wave transformation

$$\begin{aligned} \begin{aligned} u(x,t)=U_{1}(\xi )e^{i\psi (x,t)},\ \ v(x,t)=U_{2}(\xi )e^{i\psi (x,t)},\ \ \xi =\frac{l}{\beta }\left( x+\frac{1}{\Gamma (\beta )}\right) ^{\beta } +\frac{c}{\beta }\left( t+\frac{1}{\Gamma (\beta )}\right) ^{\beta },\\ \psi (x,t)=-\frac{\omega }{\beta }\left( x+\frac{1}{\Gamma (\beta )}\right) ^{\beta }+\frac{\kappa }{\beta }\left( t+\frac{1}{\Gamma (\beta )}\right) ^{\beta }+\theta _{0}, \end{aligned} \end{aligned}$$
(2)

where \(U(\xi )\) and \(V(\xi )\) are the wave’s amplitude component. c, \(\psi (x,t)\), \(\omega\), \(\kappa\), and \(\theta _{0}\) represent the frequency, the phase component, the wave number and the phase constant, respectively.

Substituting Eq. (2) into Eqs. (1), we obtain the imaginary component

$$\begin{aligned} (c-2\alpha _{j}\omega l)U_{j}^{\prime }+2\omega l(3l_{j}+m_{j}-g_{j})U_{j}^{2}U_{j}^{\prime }=0,\ \ j=1,2. \end{aligned}$$
(3)

From Eq. (3), we have

$$\begin{aligned} c=2\alpha _{j}\omega l,\ \ g_{j}=3l_{j}+m_{j},\ \ j=1,2. \end{aligned}$$
(4)

From Eq. (4), we known that the soliton speed should be equal. So we have

$$\begin{aligned} \alpha _{1}=\alpha _{2}=\alpha . \end{aligned}$$
(5)

Similarly, when substituting Eq. (2) into Eqs. (1), we can also obtain the real part

$$\begin{aligned} \begin{aligned} \alpha _{j}l^{2}U_{j}^{\prime \prime }-(\alpha _{j}\omega ^{2}+\kappa )U_{j}+F(U_{j}^{2})U_{j} +(l_{j}+m_{j}+g_{j})\omega _{j}^{2}H_{j}^{3}-6l_{j}l^{2}U_{j}-l^{2}(3l_{j}+m_{j}+g_{j})U_{j}^{2}U_{j}^{\prime \prime }\\ -k_{j}U_{j^{*}}=0, \ \ j=1,2,\ j^{*}=3-j. \end{aligned} \end{aligned}$$
(6)

Due to the balancing rectitude, we assume that \(U_{j}=U_{j^{*}}\). When \(F(h)=sh\), Eq. (6) can be transformed into

$$\begin{aligned} \alpha l^{2}U_{j}^{\prime \prime }-(\alpha _{j}\omega ^{2}+\kappa +k_{j})U_{j} +[s_{j}+2(g_{j}-l_{j})\omega _{j}^{2}]U_{j}^{3}-6l_{j}l^{2}U_{j}(U_{j}^{\prime })^{2}-2l^{2}g_{j}U_{j}^{2}U_{j}^{\prime \prime }=0,\ \ j=1,2. \end{aligned}$$
(7)

Here, Eq. (7) is rewritten as

$$\begin{aligned} \alpha l^{2}U_{j}^{\prime \prime }-(\alpha _{j}\omega ^{2}+\kappa +k_{j})U_{j} +s_{j}U_{j}^{3}=0,\ \ j=1,2, \end{aligned}$$
(8)

when \(l_{j}=g_{j}=0\).

Qualitative analysis

When \(\alpha l\ne 0\), two-dimensional dynamic system of Eq. (8) can be rewritten as

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{dU_{j}}{d\xi }=z_{j},\\ \frac{dz_{j}}{d\xi }=\Im _{3j}U_{j}^{3}-\Im _{1j}U_{j}, \end{array}\right. } \end{aligned}$$
(9)

with Hamiltonian function

$$\begin{aligned} H(U_{j},z_{j})=\frac{1}{2}z_{j}^{2}-\frac{\Im _{3j}}{4}U_{j}^{4}+\frac{\Im _{1j}}{2}U_{j}^{2}=h, \end{aligned}$$
(10)

where \(\Im _{3j}=\frac{\alpha _{j}\omega ^{2}+\kappa +k_{j}}{\alpha l^{2}}\) and \(\Im _{1j}=\frac{s_{j}}{\alpha l^{2}}\).

Assume that \(G(U_{j})=\Im _{3j}U_{j}^{3}-\Im _{1j}U_{j}\) is the abscissa of the equilibrium point. Further suppose that \(\textbf{M}(U_{j},0)=\left( \begin{matrix} 0 & 1\\ 3\Im _{3j}U_{j}^{2}-\Im _{1j}& 0 \end{matrix}\right)\) is the coefficient matrix of (9) at the equilibrium point. Then, we obtain

$$\begin{aligned} \textbf{det}(\textbf{M}(U_{j},0))=-G'(U_{j}),\ \ j=1,2. \end{aligned}$$
(11)

Based on the theory of planar dynamical systems, we can draw the following conclusions:

If \(\Im _{1}\Im _{3}<0\), the system (9) has one equilibrium point (0, 0).

If \(\Im _{1}\Im _{3}>0\), the system (9) has three equilibrium point (0, 0), \(\left( \sqrt{\frac{\Im _{1j}}{\Im _{3j}}},0\right)\), \(\left( -\sqrt{\frac{\Im _{1j}}{\Im _{3j}}},0\right)\).

Due to the fact that Eqs.(1) is a coupled equation. Therefore, system (9) would also be two possibilities. When \(j=1\), we draw the planar phase portrait of system (9) as shown in Fig. 1.

Fig. 1
figure 1

2D phase portrait of system (9). (a) \(\Im _{11} < 0, \Im _{31} > 0\) (b) \(\Im _{11} > 0, \Im _{31} < 0\) (c) \(\Im _{11} < 0, \Im _{31} < 0\) (d) \(\Im _{11} > 0, \Im _{31} > 0\)

Full size image

Qualitative analysis with perturbation term

In this section, two small perturbation term to the system (9) are added as follows

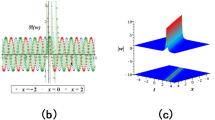
$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{dU_{j}}{d\xi }=z_{j},\\ \frac{dz_{j}}{d\xi }=\Im _{3j}U_{j}^{3}-\Im _{1j}U_{j}+f_{j}(\xi ), \end{array}\right. } \end{aligned}$$
(12)

where \(f_{j}(\xi )=A_{j}\sin (\varpi \xi )\) represents the periodic disturbance term. \(f_{j}(\xi )=A_{j}e^{-0.07\xi }\) stands for the small disturbance. \(A_{j}\) and \(\varpi\) represent the amplitude and the frequency of system (12), respectively. By giving the parameters \(\Im _{11},\Im _{31},A,\varpi\), the two-dimensional, three-dimensional phase portrait, and Paincaré section diagrams of system (12) are drawn as shown in Figs. 2, 3, 4, and 5. Moreover, the branch phase diagram of system (12) are plotted as shown in Figs. 6 and 7.

Fig. 2
figure 2

The chaotic behaviors of system (12) with \(\Im _{11}=1,\Im _{31}=-5,A=1.6,\varpi =0.8\). (a) 2D phase portrait (b) 3D phase portrait (c) Paincaré section.

Full size image
Fig. 3
figure 3

The chaotic behaviors of system (12) with \(\Im _{1}=1,\Im _{31}=-5,A=1.6\). (a) 2D phase portrait (b) 3D phase portrait (c) Paincaré section.

Full size image
Fig. 4
figure 4

The chaotic behaviors of system (12) with \(\Im _{11}=-1,\Im _{31}=-5,A=1.6,\varpi =1.6\). (a) 2D phase portrait (b) 3D phase portrait (c) Paincaré section.

Full size image
Fig. 5
figure 5

The chaotic behaviors of system (12) with \(\Im _{11}=-1,\Im _{31}=-5,A=1.6\). (a) 2D phase portrait (b) 3D phase portrait (c) Paincaré section.

Full size image
Fig. 6
figure 6

The bifurcation portraits of system (12) with \(\Im _{11}=-1,\Im _{31}=-1\), \(r=\sqrt{z_1^{2}+U_1^{2}}\). (a) \(\varpi = 0.8\) (b) \(\varpi = 1\) (c) \(\varpi = 1.2\).

Full size image
Fig. 7
figure 7

The bifurcation portraits of system (12) with \(\Im _{11}=1,\Im _{31}=-1\), \(r=\sqrt{z_1^{2}+U_1^{2}}\). (a) \(\varpi = 0.8\) (b) \(\varpi = 1\) (c) \(\varpi = 1.2\).

Full size image

Solitary wave solutions of Eqs. (1)

In this section, we first assume that \(h_{0}=H(0,0)=0\), \(h_{1}=H(\pm \sqrt{\frac{\Im _{1j}}{\Im _{3j}}},0)=\frac{\Im _{1j}^{2}}{4\Im _{3j}}\). According to the analysis theory of planar dynamical systems, we can provide the solitary wave solutions of Eqs. (1).

\(\Im _{1j}>0,\) \(\Im _{3j}>0,\) \(0<h<\frac{\Im _{1j}^{2}}{4\Im _{3j}}\)

Then system (9) is rewritten as

$$\begin{aligned} z_{j}^{2}=\frac{\Im _{3j}}{2}\left( U_{j}^{4}-\frac{2\Im _{1j}}{\Im _{3j}}U_{j}^{2}+\frac{4h}{\Im _{3j}}\right) =\frac{\Im _{1}}{2}\left( \vartheta _{1h}^{2}-U_{j}^{2}\right) \left( \vartheta _{2h}^{2}-U_{j}^{2}\right) , \end{aligned}$$
(13)

where \(\vartheta _{1h}^{2}=\frac{\Im _{1j}+\sqrt{\Im _{1j}^{2}-4\Im _{3j}h}}{\Im _{3j}}\) and \(\vartheta _{2h}^{2}=\frac{\Im _{1j}-\sqrt{\Im _{1j}^{2}-4\Im _{3j}h}}{\Im _{3j}}\).

Plugging (13) into \(\frac{dU_{j}}{d\xi }=z_{j}\) and integrating it, the Jacobian function solutions are given

$$\begin{aligned} \begin{aligned} u_{1}(x,t)=\pm \vartheta _{1h}\textbf{sn}\left( \vartheta _{2h}\sqrt{\frac{\Im _{31}}{2}}\left( \frac{l}{\beta }\left( x+\frac{1}{\Gamma (\beta )}\right) ^{\beta } +\frac{c}{\beta }\left( t+\frac{1}{\Gamma (\beta )}\right) ^{\beta }\right) ,\frac{\vartheta _{1h}}{\vartheta _{2h}}\right) \textbf{e}^{i(-\frac{\omega }{\beta }(x+\frac{1}{\Gamma (\beta )})^{\beta }+\frac{\kappa }{\beta }(t+\frac{1}{\Gamma (\beta )})^{\beta }+\theta _{0})}, \end{aligned} \\ \begin{aligned} v_{1}(x,t)=\pm \vartheta _{1h}\textbf{sn}\left( \vartheta _{2h}\sqrt{\frac{\Im _{32}}{2}}\left( \frac{l}{\beta }\left( x+\frac{1}{\Gamma (\beta )}\right) ^{\beta } +\frac{c}{\beta }\left( t+\frac{1}{\Gamma (\beta )}\right) ^{\beta }\right) ,\frac{\vartheta _{1h}}{\vartheta _{2h}}\right) \textbf{e}^{i(-\frac{\omega }{\beta }(x+\frac{1}{\Gamma (\beta )})^{\beta }+\frac{\kappa }{\beta }(t+\frac{1}{\Gamma (\beta )})^{\beta }+\theta _{0})}. \end{aligned} \end{aligned}$$

\(\Im _{1j}>0,\) \(\Im _{3j}>0,\) \(h=\frac{\Im _{1j}^{2}}{4\Im _{3j}}\)

When \(\vartheta _{1h}^{2}=\vartheta _{2h}^{2}=\frac{\Im _{1j}}{\Im _{3j}}\), the solitary wave of Eqs. (1) are given

$$\begin{aligned} \begin{aligned} u_{2}(x,t)=\pm \sqrt{\frac{\Im _{11}}{\Im _{31}}}\textbf{tanh}\left( \sqrt{\frac{\Im _{31}}{2}}\left( \frac{l}{\beta }\left( x+\frac{1}{\Gamma (\beta )}\right) ^{\beta } +\frac{c}{\beta }\left( t+\frac{1}{\Gamma (\beta )}\right) ^{\beta }\right) \right) \textbf{e}^{i(-\frac{\omega }{\beta }(x+\frac{1}{\Gamma (\beta )})^{\beta }+\frac{\kappa }{\beta }(t+\frac{1}{\Gamma (\beta )})^{\beta }+\theta _{0})}, \end{aligned} \\ \begin{aligned} v_{2}(x,t)=\pm \sqrt{\frac{\Im _{12}}{\Im _{32}}}\textbf{tanh}\left( \sqrt{\frac{\Im _{32}}{2}}\left( \frac{l}{\beta }\left( x+\frac{1}{\Gamma (\beta )}\right) ^{\beta } +\frac{c}{\beta }\left( t+\frac{1}{\Gamma (\beta )}\right) ^{\beta }\right) \right) \textbf{e}^{i(-\frac{\omega }{\beta }(x+\frac{1}{\Gamma (\beta )})^{\beta }+\frac{\kappa }{\beta }(t+\frac{1}{\Gamma (\beta )})^{\beta }+\theta _{0})}. \end{aligned} \end{aligned}$$

\(\Im _{1j}<0,\) \(\Im _{3j}<0,\) \(\frac{\Im _{1j}^{2}}{4\Im _{3j}}<h<0\)

Then system (9) is rewritten as

$$\begin{aligned} z_{j}^{2}=-\frac{\Im _{3j}}{2}\left( -U_{j}^{4}+\frac{2\Im _{1j}}{\Im _{3j}}U_{j}^{2}-\frac{4h}{\Im _{3j}}\right) =-\frac{\Im _{3j}}{2}\left( U_{j}^{2}-\vartheta _{3h}^{2}\right) \left( \vartheta _{4h}^{2}-U_{j}^{2}\right) , \end{aligned}$$
(14)

where \(\vartheta _{3h}^{2}=\frac{\Im _{1j}-\sqrt{\Im _{1j}^{2}-4\Im _{3j}h}}{\Im _{3j}}\) and \(\vartheta _{4h}^{2}=\frac{\Im _{1j}+\sqrt{\Im _{1j}^{2}-4\Im _{3j}h}}{\Im _{3j}}\).

Plugging (14) into \(\frac{dU_{j}}{d\xi }=z_{j}\) and integrating it, the Jacobian function solutions are given

$$\begin{aligned} \begin{aligned} u_{3}(x,t)=\pm \vartheta _{31}\textbf{dn}\left. \left( \vartheta _{31}\sqrt{-\frac{\Im _{31}}{2}}\left( \frac{l}{\beta }\left( x+\frac{1}{\Gamma (\beta )}\right) ^{\beta } +\frac{c}{\beta }\left( t+\frac{1}{\Gamma (\beta )}\right) ^{\beta }\right) \right) ,\frac{\sqrt{\vartheta _{4h}^{2}-\vartheta _{3h}^{2}}}{\vartheta _{4h}}\right) \\ \textbf{e}^{i(-\frac{\omega }{\beta }(x+\frac{1}{\Gamma (\beta )})^{\beta }+\frac{\kappa }{\beta }(t+\frac{1}{\Gamma (\beta )})^{\beta }+\theta _{0})}, \end{aligned} \\ \begin{aligned} v_{3}(x,t)=\pm \vartheta _{32}\textbf{dn}\left. \left( \vartheta _{32}\sqrt{-\frac{\Im _{32}}{2}}\left( \frac{l}{\beta }\left( x+\frac{1}{\Gamma (\beta )}\right) ^{\beta } +\frac{c}{\beta }\left( t+\frac{1}{\Gamma (\beta )}\right) ^{\beta }\right) \right) ,\frac{\sqrt{\vartheta _{4h}^{2}-\vartheta _{3h}^{2}}}{\vartheta _{4h}}\right) \\ \textbf{e}^{i(-\frac{\omega }{\beta }(x+\frac{1}{\Gamma (\beta )})^{\beta }+\frac{\kappa }{\beta }(t+\frac{1}{\Gamma (\beta )})^{\beta }+\theta _{0})}. \end{aligned} \end{aligned}$$

\(\Im _{1j}<0,\) \(\Im _{3j}<0,\) \(h=0\)

When \(\vartheta _{3h}^{2}=\frac{2\Im _{1j}}{\Im _{3j}},\vartheta _{4h}^{2}=0\), the solitary wave of Eqs. (1) are given

$$\begin{aligned} \begin{aligned} u_{4}(x,t)=\pm \sqrt{\frac{2\Im _{11}}{\Im _{31}}}\textbf{sech}\left. \left( \sqrt{\Im _{11}}\left( \frac{l}{\beta }\left( x+\frac{1}{\Gamma (\beta )}\right) ^{\beta } +\frac{c}{\beta }\left( t+\frac{1}{\Gamma (\beta )}\right) ^{\beta }\right) \right) \right) \textbf{e}^{i(-\frac{\omega }{\beta }(x+\frac{1}{\Gamma (\beta )})^{\beta }+\frac{\kappa }{\beta }(t+\frac{1}{\Gamma (\beta )})^{\beta }+\theta _{0})}, \end{aligned} \\ \begin{aligned} v_{4}(x,t)=\pm \sqrt{\frac{2\Im _{12}}{\Im _{32}}}\textbf{sech}\left. \left( \sqrt{\Im _{12}}\left( \frac{l}{\beta }\left( x+\frac{1}{\Gamma (\beta )}\right) ^{\beta } +\frac{c}{\beta }\left( t+\frac{1}{\Gamma (\beta )}\right) ^{\beta }\right) \right) \right) \textbf{e}^{i(-\frac{\omega }{\beta }(x+\frac{1}{\Gamma (\beta )})^{\beta }+\frac{\kappa }{\beta }(t+\frac{1}{\Gamma (\beta )})^{\beta }+\theta _{0})}. \end{aligned} \end{aligned}$$

\(\Im _{1j}<0,\) \(\Im _{3j}<0,\) \(h>0\)

Then system (9) is rewritten as

$$\begin{aligned} z_{j}^{2}=-\frac{\Im _{3j}}{2}\left( -U_{j}^{4}+\frac{2\Im _{1j}}{\Im _{3j}}U_{j}^{2}-\frac{4h}{\Im _{3j}}\right) =-\frac{-\Im _{3j}}{2}\left( \vartheta _{5h}^{2}+U_{j}^{2}\right) \left( \vartheta _{6h}^{2}-U_{j}^{2}\right) , \end{aligned}$$
(15)

where \(\vartheta _{5h}^{2}=\frac{\Im _{1j}+\sqrt{\Im _{1j}^{2}-4\Im _{3j}h}}{\Im _{3j}}\) and \(\vartheta _{6h}^{2}=\frac{\Im _{1j}-\sqrt{\Im _{1j}^{2}-4\Im _{3j}h}}{\Im _{3j}}\).

Plugging (15) into \(\frac{dU_j}{d\xi }=z_{j}\) and integrating it, the Jacobian function solutions are given

$$\begin{aligned} \begin{aligned} u_{5}(x,t)=\pm \vartheta _{6h}\textbf{cn}\left. \left. \left( \sqrt{-\frac{\Im _{31}(\vartheta _{5h}^{2}+\vartheta _{6h}^{2})}{2}}\left( \frac{l}{\beta }\left( x+\frac{1}{\Gamma (\beta )}\right) ^{\beta } +\frac{c}{\beta }\left( t+\frac{1}{\Gamma (\beta )}\right) ^{\beta }\right) \right) \right) ,\frac{\vartheta _{6h}}{\sqrt{\vartheta _{5h}^{2}+\vartheta _{6h}^{2}}}\right) \\ \textbf{e}^{i(-\frac{\omega }{\beta }(x+\frac{1}{\Gamma (\beta )})^{\beta }+\frac{\kappa }{\beta }(t+\frac{1}{\Gamma (\beta )})^{\beta }+\theta _{0})}, \end{aligned} \\ \begin{aligned} v_{5}(x,t)=\pm \vartheta _{6h}\textbf{cn}\left. \left. \left( \sqrt{-\frac{\Im _{32}(\vartheta _{5h}^{2}+\vartheta _{6h}^{2})}{2}}\left( \frac{l}{\beta }\left( x+\frac{1}{\Gamma (\beta )}\right) ^{\beta } +\frac{c}{\beta }\left( t+\frac{1}{\Gamma (\beta )}\right) ^{\beta }\right) \right) \right) ,\frac{\vartheta _{6h}}{\sqrt{\vartheta _{5h}^{2}+\vartheta _{6h}^{2}}}\right) \\ \textbf{e}^{i(-\frac{\omega }{\beta }(x+\frac{1}{\Gamma (\beta )})^{\beta }+\frac{\kappa }{\beta }(t+\frac{1}{\Gamma (\beta )})^{\beta }+\theta _{0})}. \end{aligned} \end{aligned}$$

Numerical simulations

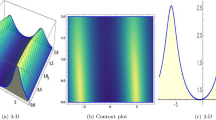
In this section, we plotted the solutions \(u_{1}(x,t)\) and \(u_{2}(x,t)\) including three-dimensional graph, two-dimensional graph, density graph, and counter graph as shown in Figs. 8 and 9.

Fig. 8
figure 8

The solution \(u_{1}(x,t)\) with \(\alpha =1,l=1,s_{1}=1,w=1,\kappa =2,k_{1}=-2,c=2,\alpha _{1}=1,h=\frac{3}{16}\). (a) 3D graph (b) Density graph (c) Contour graph (d) 2D graph

Full size image
Fig. 9
figure 9

The solution \(u_{2}(x,t)\) with \(\alpha =1,l=1,s_{1}=1,w=1,\kappa =2,k_{1}=-2,c=2,\alpha _{1}=1,h=\frac{1}{4}\). (a) 3D graph (b) Density graph (c) Contour graph (d) 2D graph

Full size image

Conclusion

In the article, we study the bifurcation, the chaotic behaviors and the solitary wave solutions for Eqs. (1) in the areas of optics and optical communication by using the theory of dynamical system, we draw the planar phase diagram of two-dimensional dynamical system. In addition, we draw plane phase diagrams, three-dimensional phase diagrams, and Paincaré section of the perturbed systems by adding periodic disturbances and small disturbances, respectively. For different initial values, we draw the planar phase diagram and three-dimensional phase diagram in red and blue, respectively. Based on the theory of planar dynamic system analysis, we obtain the solution to Eqs. (1). By using mathematical software, the three-dimensional, two-dimensional, density, and contour maps of these solutions are displayed. Compared with existing literature26, we not only obtained the dynamic behavior of system (9) and its perturbed system, but also obtained the Jacobian function solution of system (1) under specific parameter conditions. These have not been reported in other literature. The dynamic behavior and solitary wave solutions of fractional order nonlinear partial differential equations are currently hot topics in research, and in future studies, we will continue to focus on research in this area. Moreover, we will consider more complex fractional order nonlinear partial differential equations.