Simulating runoff changes and evaluating under climate change using CMIP6 data and the optimal SWAT model: a case study

Abstract

This study examines the influence of climate change on hydrological processes, particularly runoff, and how it affects managing water resources and ecosystem sustainability. It uses CMIP6 data to analyze changes in runoff patterns under different Shared Socioeconomic Pathways (SSP). This study also uses a Deep belief network (DBN) and a Modified Sparrow Search Optimizer (MSSO) to enhance the runoff forecasting capabilities of the SWAT model. DBN can learn complex patterns in the data and improve the accuracy of runoff forecasting. The meta-heuristic algorithm optimizes the models through iterative search processes and finds the optimal parameter configuration in the SWAT model. The Optimal SWAT Model accurately predicts runoff patterns, with high precision in capturing variability, a strong connection between projected and actual data, and minimal inaccuracy in its predictions, as indicated by an ENS score of 0.7152 and an R² coefficient of determination of 0.8012. The outcomes of the forecasts illustrated that the runoff will decrease in the coming years, which could threaten the water source. Therefore, managers should manage water resources with awareness of these conditions.

Introduction

Water is a crucial natural resource necessary for human life, agriculture, and economic development. Proper management of water resources is essential due to its vulnerability to climate change and uneven distribution across regions. Water is integral to reaching carbon neutrality, particularly through sustainable energy production via hydroelectric power, which helps lower greenhouse gas emissions and reduces dependence on fossil fuels. Furthermore, hydropower facilitates the shift towards more sustainable urban energy systems and industrial practices. Responsible management of water resources is vital for the sustainable growth of communities, economies, and the environment.

Urban areas and industries are increasingly adopting sustainable methods, with water resources being vital to this shift. Water is essential in numerous processes, including cooling and manufacturing, making effective water management critical for supporting green initiatives. However, global warming’s effects, such as droughts and floods, can significantly impact water availability and quality, emphasizing the need for responsible management. Recognizing how climate factors like precipitation, temperature, and evapotranspiration influence hydrological processes, particularly runoff, is crucial for advancing sustainability. Rising temperatures speed up the water cycle and enhance evaporation, altering precipitation and runoff patterns, which necessitates adaptive water management strategies to maintain ecosystem health and resilience.

Recognizing the effects of climate change on the water cycle is vital for managing water resources effectively. Decision-makers, water management agencies, and relevant parties must evaluate how climate change influences water supply to make educated choices and prepare for the future. An integrated strategy that tackles the impacts of climate change, supports sustainable practices, and advocates for efficient water usage and conservation is essential. By integrating these factors, policymakers can secure vital water resources for future generations and promote a more resilient and sustainable future.

Global Climate Models (GCMs) are essential tools for predicting and understanding climate change, and the Coupled Model Intercomparison Project Phase 6 (CMIP6) has improved upon previous versions by enhancing spatial patterns and reducing deviations. These models play a crucial role in forecasting climate change, and their ability to minimize uncertainties is important for making informed decisions. However, it is important to consider uncertainties from emission scenarios, climate forcing, and hydrological models when interpreting projections based on CMIP6 GCMs. By utilizing GCMs and tools like the SWAT (Soil and Water Assessment Tool), we can improve our understanding of climate change and its impact on hydrological variables, leading to more effective water resource management and planning for the future.

The integration of hydrological processes in models like SWAT (Soil and Water Assessment Tool) coupled with CMIP6 Global Climate Models provides valuable insights into the impact of climate variability and land use changes on water resources. This combination allows for the prediction of hydrological responses to changing climate patterns, making SWAT a powerful tool for understanding potential shifts in watershed hydrology¹. The use of various models and methods, including Convolutional Neural Networks (CNNs) and Variation Mode Decomposition (VMD), further enhances the understanding of runoff patterns and changes. These tools and techniques are essential for developing sustainable water management strategies and addressing the challenges posed by climate change².

In the following part, some different works of various researchers have been investigated.

Ridwansyah et al.³ utilized the Soil and Water Assessment Tool (SWAT) model to investigate the impacts of land use changes and climate change on groundwater and surface runoff. The SWAT model, a semi-distributed, physically based hydrological tool, was applied using various data sources, including discharge records, land use data, and simulated and projected climate data. The model’s validation and calibration showed acceptable performance for hydrological simulations. The results indicated that land use changes led to an overall increase in runoff, while the contribution of base flow to annual streamflow decreased. Comparisons between current and projected climate conditions suggested a rise in the Qmax/Qmin ratio in specific years, highlighting the potential impacts of climate change on hydrological dynamics.

Song et al.⁴ proposed a methodology to create two types of two-dimensional features, Base Flow Features (BFF) and Surface Flow Features (SFF), using groundwater level and Soil Conservation Service curve number data. They utilized a Convolutional Neural Network (CNN) to assess the suitability of these features for simulating daily runoff. The CNN structure was modified to derive constant parameters and handle multi-input data. The daily runoff simulations indicated moderate performance using SFF and BFF, suggesting that these features hold sufficient value as input data for the CNN model.

Li et al.⁵, analyzed the response of the hydrological runoff process to climate change in typical watersheds of the Changbai Mountains, China, providing insights for sustainable water resource management. They calibrated and verified the HEC-HMS hydrological model using daily rainfall-runoff data from 2006 to 2017, confirming its effectiveness. By downscaling rainfall data from SSP5-8.5 and SSP2-4.5 scenarios, they predicted the runoff response to climate change. The model indicated increased rainfall and altered distribution, with a certainty coefficient of 0.705. The study found that outlet flow increased during the rainy and snowy seasons, and peak flow shifted from July-August to August-September.

A study conducted by Das et al.⁶ investigated the impact of climate change on the flow of the Gomati River catchment in northeast India. They used the Group Method of Data Handling (GMDH) method to simulate the relationship between rainfall and runoff in the river catchment using data from 2008 to 2009. By analyzing the downscaled outputs of the Hadley Centre Global Environment Model version 2 (HadGEM2-ES) broad flow model, they assessed the effects of climate change on the Gomati River basin. The study projected changes for the 2030s, 2040s, and 2050s, providing valuable insights for developing adaptive plans and policies for sustainable water resource management in northeast Tripura.

Wu et al.⁷ roposed a deep-learning model for daily river runoff prediction, combining VMD decomposition with CNN and BiLSTM-attention networks. The model was optimized using Bayesian Optimization Algorithm (BOA) and outperformed other models, with lower RMSEs of 3.54 and 15.23 at two test stations. The model exhibited improved adaptability and performance under various hydrological conditions, offering valuable guidance for flood warning and water resource management.

Chadalawada et al.⁸ introduced a novel method for constructing models using adaptable modeling frameworks and machine learning. Their approach, utilizing genetic programming, focused on rainfall-runoff modeling with physical significance. The algorithm was applied for short-term predictions, similar to neural networks. The framework’s effectiveness was assessed in Alabama’s Blackwater River basin. The resulting model configurations aligned with previous fieldwork and research findings, showcasing the method’s accuracy and potential for practical applications in hydrology.

Cai et al.⁹ presented a hybrid model for groundwater level simulations that combined water balance-based procedures with deep learning architectures. The physics-informed approach allowed the model to infer groundwater procedures and geological structures not directly observed. Compared to pure deep learning models, the hybrid model demonstrated improved prediction accuracy, robustness, and generality in 91 groundwater level modeling cases. The study offered an enhanced data-driven alternative to complex groundwater models, contributing to a better understanding of hydrological processes.

Heras et al.¹⁰ proposed MIKA-SHA, a system that could automatically generate models for rainfall-runoff, taking into account the spatial differences in catchments. The MIKA-SHA was trained on versatile modeling frameworks but could adjust to other consistent components. MIKA-SHA’s effectiveness was evaluated on the Rappahannock River basin, where it discovered two ideal models that performed well in forecasting hydrographs and closely matched the observed reactions. The models that were created were consistent with prior research and fieldwork, and allowed hydrologists to easily interpret them. MIKA-SHA-induced semi-distributed models were more effective than the existing lumped models for the basin, and they could provide deeper hydrological insights.

Jiang et al.¹¹ utilized interpretive Deep Learning (DL) techniques to investigate flood prediction across the contiguous United States. Through the application of two methodologies to identify patterns within LSTM networks for runoff modeling, they discovered three significant input-output relationships associated with flooding: snowmelt (10.1%), recent rainfall (60.9%), and historical rainfall (29.0%). Most catchments demonstrated a singular flooding mechanism, with either snowmelt, recent rainfall, or historical rainfall serving as the primary influencing factor. The study showed the LSTM networks’ capacity to selectively retain and discard information based on different flood types, underscoring their versatility in simulating a range of hydrological processes.

The prediction and understanding of runoff patterns are important topics that have received significant attention in the literature. Researchers have made substantial contributions to their respective fields, advancing knowledge and providing insights. However, there is a need for further research that incorporates the latest climate data, such as CMIP6, and explores the impacts of different socioeconomic pathways on future runoff patterns. Advanced machine learning techniques are also necessary to understand the potential effects of climate and socioeconomic changes on runoff dynamics, enabling better decision-making for water resource management.

This study’s main goal is eliminating the shortages of the existing models of runoff changes under the influence of climate change and different socioeconomic pathways. Through the use of CMIP6 data, this study seeks to comprehensively analyze future runoff trends, taking into account climate variables such as precipitation, temperature, and evapotranspiration. A novel approach to enhancing the accuracy of runoff predictions involves integrating DBN and Amended Sparrow Search Optimization into the SWAT method. The primary objective of this investigation is developing an advanced tool for predicting runoff, which can aid in decision-making processes regarding water resource management and adaptation strategies. This investigation’s findings will offer valuable comprehension into the potential impacts of any change in climate and different socioeconomic factors on future runoff patterns. Such information will empower stakeholders to make knowledgeable decisions that ensure the sustainability and resilience of water resources in the face of changing climatic conditions.

Method and material

Case study

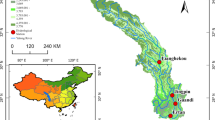
The Jinsha River traverses China’s Qinghai, Sichuan, and Yunnan provinces. The study area is located in the upper reaches of the Jinsha River in China, and the coordinates are approximately 28.35°N, 100.22°E It has a range of climates and is a vital tributary of the Yangtze River. The subtropical region has the most significant annual temperature variation and precipitation. The cold Qinghai-Tibet Plateau, where the river’s upper half is located, has brief summers and moderate winters. Snowfall is frequent, and rainfall is little. The climate becomes more bearable as the river moves away from the plateau, with sporadic mild winters and pleasant summers. Every year, more rain falls, particularly during the monsoon season, resulting in catastrophic downpours. Further down the river, the annual precipitation ranges from 800 to 1500 mm in the subtropical region, with hot summers and mild winters. The range of summer temperatures is 25 °C to 35 °C, while the range of winter temperatures is 5 °C to 15 °C. Fig.  1. shows the Jinsha River location, which Google Maps has obtained.

Fig. 1

The Jinsha River location¹².

Data description

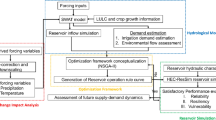
This investigation’s geographical data has been collected online. The datasets included a Digital Elevation Model (DEM), soil kind, and land usage information. The DEM had a spatial resolution of 1 km, and the land use information in 2022 had a resolution of 1:250,000. The soil data, with a precision of 0.25°× 0.25°, was taken from the Food and Agriculture Organization’s harmonized global soil database. These geographical data are crucial to implement the SWAT hydrological model. The SWAT model simulates the complex interactions between land use, topography, soil properties, and climate conditions that affect runoff and streamflow production in watersheds. They are essential data as input factors hydrological model. The present research used meteorological data spanning from 1992 to 2022 as a foundational dataset to predict climatic characteristics via the application of climate models. Historical simulations, including 1992 to 2022, have been carried out, while future forecasts have been formulated throughout 2023 to 2100. These projections are based on two distinct scenarios, namely SSP12.6 and SSP58.5. The datasets included daily precipitation measurements, mean air temperature, highest temperature of air, and minimum temperature of air. The SWAT model used daily rainfall, highest temperature of air, and minimum temperature of air data to estimate runoff changes. The monthly runoff data collected from the Panzhihua Hydrological Station spanning 1992 to 2022 has been acquired to validate and calibrate the optimum Soil and Water Assessment Tool hydrological system. The 75% data has been used to validate and 25% data has been utilized to calibrate model.

Climate model

The present research used from four General Circulation Models (GCMs) in order to simulate forthcoming meteorological data. Table 1 presents the facts about the GCMs model.

Table 1 Specifications of CMIP6 models used in this research.

Downscaled climate datasets from CMIP6 models offer significant insights into regional climate patterns, encompassing crucial meteorological factors like precipitation and temperature¹³. These datasets have been effectively employed as inputs to facilitate the operation of the SWAT model, enabling the simulation of hydrological processes that contribute to generating runoff.

The study used the version 4.1.1 of the Weather Research and Forecasting Model (WRF) to downscale global climate model outputs from the CMIP6 dataset¹⁴. The WRF model is widely used as a regional climate model, enabling the simulation of atmospheric processes at enhanced spatial resolution. This downscaling method includes local-scale climatic characteristics, topography effects, and regional climate dynamics. The downscaled outputs contribute to understanding climate variations at a finer spatial scale, allowing for better understanding of regional climate patterns and potential consequences. The model integrates various physical parameterizations, such as radiation, microphysics, boundary layer, and land surface schemes, allowing for simulation of interactions among the atmosphere, land surface, and ocean. This downscaling process provides downscaled climate forecasts that include local-scale processes and provide a more comprehensive depiction of climatic variables within the study region. This enables a more comprehensive evaluation of climate change’s effects on specific regions and aids in the formulation of tailored adaptation measures. The study analyzes Shared Socioeconomic Pathways (SSP). scenarios to predict climate change, focusing on pessimistic (SSP5-8.5) and optimistic (SSP1-2.6) scenarios. It evaluates the effects of socio-economic routes on runoff conditions and water resources, aiming to gain insights into the hydrological cycle and water resources.

Optimal hydrological model

SWAT model

Simulating runoff can be done effectively with the SWAT hydrological model, which accurately represents the intricate procedure in the hydrological cycle¹⁵. The US Department of Agriculture’s Agricultural Research Service has created a model that forecasts the runoff and assesses the potential impact on water resources. This model relies on physical factors and is semi-distributed, enabling researchers to make knowledgeable predictions. Integrating data from climate models like the CMIP6 GCMs, the combination of the model with climate change and socioeconomic scenarios can enhance its potency in projecting how changing climatic conditions might affect runoff. Decision-makers can use this approach to create plans that will help them adjust to and reduce the impact of these changes¹⁶.

The SWAT model has enhanced our comprehension of runoff procedures and how they react to environmental conditions. Researchers can analyze the complicated interplay between land utilization, climate, and water resources by precisely replicating the hydrological cycle and integrating climate change forecasts¹⁷. Knowledgeable decision-making requires vital knowledge, including identifying vulnerable areas, prioritizing conservation efforts, and developing sustainable water management techniques that adapt to changing conditions¹⁸. The SWAT model’s ongoing refinement and application contribute to tackling challenges related to runoff and advancing the field of hydrological science.

Using a combination of empirical and physically-based principles, the SWAT model employs the SCS-CN (Soil Conservation Service Curve Number) approach for simulating the relationship between rainfall and runoff. This approach considers various factors, such as the soil’s initial abstraction capacity, antecedent moisture conditions, and rainfall intensity, to estimation of the runoff. In the Soil and Water Assessment Tool model, the CN approach is utilized to calculate streamflow; moreover, it is deemed the most feasible approach to calculate Curve Number in the USDA model. The Curve Number approach segregates the runoff value generated by precipitation from the overall precipitation utilizing a water balance. The equations embodied in the SWAT model are implemented by the Soil Conservation Service Curve Number approach to estimate runoff¹⁸. The equations are defined in the following:

$$\:Q=\frac{{(P-{I}_{a})}^{2}}{(P-S)}\:$$

(1)

The total precipitation (mm) is represented by $\:P$. The runoff value created by precipitation (mm) is demonstrated by $\:Q$. $\:{I}_{a}$ represents the initial abstraction, which denotes to the rainfall’s portion, which is either kept or lost because of evaporation before any runoff occurs. The possible extreme maintenance after the beginning of runoff is demonstrated by $\:S$.

The values of $\:{I}_{a}$ and S are influenced by several parameters, including soil properties, land cover, and hydrological conditions present in the watershed. These parameters collectively impact the soil’s capacity to store water before producing runoff. The formulations of $\:{I}_{a}$ and S are shown as follows:

$$\:{I}_{a}=P\times\:\left(\frac{\left(0.2\right)}{\left(0.8+CN\right)}\right)$$

(2)

$$\:S=25.4(\frac{1000}{CN}-10)$$

(3)

Here, $\:{I}_{a}$ represents a fraction of the total precipitation $\:P$ in Eq. (2), and the curve number is demonstrated.

by $\:CN$. The $\:CV$ illustrates the hydrologic features of the soil and land cover in the watershed.

The possible extreme maintenance or the soil’s capacity is illustrated by $\:S$ in Eq. (3) as a function of the $\:CN$ (the curve number).

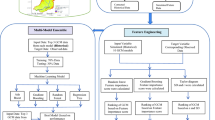
Deep belief network (DBN) model

Researchers are utilizing Deep Belief Networks (DBNs), a form of neural network, in hydrological research to enhance runoff simulations and water supply forecasts. Although successful in various domains, DBNs remain largely untapped in hydrology. The aim is to address the shortcomings of conventional hydrological models, which often cannot represent the complex nonlinear interactions between climate factors and runoff behavior. Using DBNs, researchers seek to discover hidden patterns and increase simulation accuracy, thereby gaining deeper insight into runoff dynamics. This technology can effectively model complex hydrological processes and provide more reliable forecasts in various climate scenarios. Integrating DBNs into hydrological modeling can significantly improve water resources management, flood forecasting, and climate change responses, enabling stakeholders to make informed decisions for sustainable water management. Restricted Boltzmann Machine (RBM) models provide a distinct approach to automatic decoding, differentiating them from conventional neural networks. As integral parts of Deep Belief Networks (DBNs), RBMs aim to capture and reconstruct data distributions at each layer while retaining the ability to reconstruct data space. This capability enhances the neural network’s data representation and its relevance to real-world applications. By managing the representation abilities of the network, deep models ensure RBMs can effectively handle complex data distributions.

In contrast, traditional neural networks often face challenges with multilayer test data, even though they can adjust the weights to match the training data. DBNs, which are generative models using RBM as building blocks, train each RBM layer under supervision, followed by optimization through a backpropagation algorithm. These networks are adept at extracting high-level features from training data and improving class discrimination. While multiple connections can facilitate training with fewer errors, they may increase mistakes during testing. RBM-based models emphasize a unique generation process for each layer, data space preservation, and decoding capabilities. By adjusting the data representation, DBNs increase their generalizability to real-world scenarios and are valuable for complex tasks.

Deep Belief Networks (DBNs) are advanced neural networks designed to improve generalization and manage information flow in data. They focus on understanding the core data distribution while minimizing reliance on Boltzmann machines, resulting in more accurate models. DBNs utilize a multi-layer training strategy, incorporating Restricted Boltzmann Machines (RBMs) at each layer, which are trained with supervision. Backpropagation-based algorithms refine the training process, adjusting weights to enhance performance and reduce overfitting. DBNs are particularly adept at extracting high-level features from training data, effectively capturing the relationships between different classes. This layered RBM training provides a thorough understanding of the data. DBNs have demonstrated their effectiveness across various domains, such as image recognition and language processing, thanks to their capability to model complex data distributions.

Figure 2 exhibits a Deep Belief Network architecture that illustrates the structure and interconnection of the network.

Fig. 2

A type of a DBN model.

In order to ascertain the hidden and input layer’s common distribution, the below function of energy can be used:

$$\:\text{P}\left(\text{v},\:\text{h}\right)=\frac{{\text{e}}^{-\text{E}\left(\text{v},\text{h}\right)}}{\sum\:_{\text{v},\text{h}}{\text{e}}^{-\text{E}\left(\text{v},\text{h}\right)\:}}$$

(4)

Here, $\:{\text{E}}_{\left(\text{v},\:\text{h}\right)}$ indicates the energy function of the Restricted Boltzmann Machine and can be computed by the below formula:

$$\:\text{E}\left(\text{v},\:\text{h}\right)=-\sum\:_{\text{i}=1}{\text{a}}_{\text{i}}{\text{v}}_{\text{i}}-\sum\:_{\text{j}=1}{\text{b}}_{\text{j}}{\text{h}}_{\text{j}}-\sum\:_{\text{i},\text{j}}{\text{v}}_{\text{i}}{\text{h}}_{\text{j}}{\text{w}}_{\text{i}\text{j}}$$

(5)

Here, the weight among hidden nodes and clear ones is represented by $\:{\text{w}}_{\text{i}\text{j}}$. The coefficient for the hidden nodes is illustrated by $\:{\text{b}}_{\text{j}}$, and the coefficient for the obvious nodes is demonstrated by $\:{\text{a}}_{\text{i}}$.

In this study, the log-likelihood-based random gradient decline method is utilized to offer effective training to the patterns of data. It is achieved by selecting $\:a,\:b$ factors in the correct way that generates for the Restricted Boltzmann Machine. Upon analyzing a provided sample, we can rephrase the possibility in the following manner:

$$\:\text{P}\left(\text{v}\right)=\frac{\sum\:_{\text{v}}{\text{e}}^{-\text{E}\left(\text{v},\text{h}\right)}}{\sum\:_{\text{v},\text{h}}{\text{e}}^{-\text{E}\left(\text{v},\text{h}\right)}}$$

(6)

For enhancement of the logarithm’s derivation, the random gradient has been used,

$$\:{\text{w}}_{\text{t}+1}={\text{w}}_{\text{t}}+{\upvartheta\:}\left(\text{P}\left(\left(\text{h}|\text{v}\right){\text{v}}^{\text{T}}\right)-\text{P}\left(\left(\widehat{\text{h}}|\widehat{\text{v}}\right){\widehat{\text{v}}}^{\text{T}}\right)\right)-{{\uplambda\:}\text{w}}_{\text{t}}+{\upalpha\:}{\Delta\:}{\text{w}}_{\text{t}-1}$$

(7)

$$\:{\text{a}}_{\text{t}+1}={\text{a}}_{\text{t}}+{\upvartheta\:}\left(\text{v}-\widehat{\text{v}}\right)+{\upalpha\:}{\Delta\:}{\text{a}}_{\text{t}-1}$$

(8)

$$\:{\text{b}}_{\text{t}+1}={\text{b}}_{\text{t}}+{\upvartheta\:}\left(\text{P}\left(\text{h}|\text{v}\right)-\text{P}\left(\widehat{\text{h}}|\widehat{\text{v}}\right)\right)+{\upalpha\:}{\Delta\:}{\text{b}}_{\text{t}-1}$$

(9)

Here,

$$\:\text{P}\left({\text{h}}_{\text{j}}=1|\text{v}\right)=\text{s}\text{i}\text{g}\text{m}\left({\sum\:}_{\text{i}=1}^{\text{m}}{\text{w}}_{\text{i}\text{j}}{\text{v}}_{\text{i}}+{\text{b}}_{\text{j}}\right)$$

(10)

and

$$\:\text{P}\left({\text{v}}_{\text{j}}=1|\text{h}\right)=\text{s}\text{i}\text{g}\text{m}\left({\sum\:}_{\text{i}=1}^{\text{n}}{\text{w}}_{\text{i}\text{j}}{\text{h}}_{\text{i}}+{\text{a}}_{\text{j}}\right)$$

(11)

Here, the hidden nodes’ number is indicated by $\:n$. The learning ratio is defined by $\:{\upvartheta\:}$. The logistic sigmoid function is demonstrated by $\:sigm(.)$. The weight of momentum and the weight decreasing is illustrated by $\:{\upalpha\:}$.

The optimization process is achieved by integrating the gradient-enhancement algorithm with the re-propagation algorithm. Given the complexities of addressing the error function and variations of the NP problem, traditional methods are frequently employed. To tackle this challenge, metaheuristics and the MSSO algorithm are applied to enhance the training of the Deep Belief Network by effectively adjusting its weights. Cost performance optimization has been realized by reducing the Mean Square Error (MSE), which measures the difference between the neural network’s output and the expected value, as shown in the following equation:

$$\:\text{E}\text{r}\text{r}\text{o}\text{r}=\frac{1}{\text{T}}\sum\:_{\text{j}=1}^{\text{N}}\sum\:_{\text{i}=1}^{\text{T}}{\left({\text{D}}_{\text{j}}\left(\text{i}\right)-{\text{Y}}_{\text{j}}\left(\text{i}\right)\right)}^{2}$$

(12)

Here, the data number is represented by $\:T$, and the output layer’s number is demonstrated by $\:N$. The quantity of the $\:{j}^{th}$ entity in Deep Belief Network’s output nodes at the time $\:t$ is illustrated by $\:{\text{D}}_{\text{j}}\left(\text{i}\right)$. The $\:{j}^{th}$ factor of the good quantity is demonstrated by $\:{\text{Y}}_{\text{j}}\left(\text{i}\right)$. This algorithm was utilized for the Deep Belief Network, as well as it recurrences to reach the criteria of stopping.

Optimization algorithms

The basic sparrow search optimizer

The procedure of finding the best solution for a problem while minimizing or maximizing a value is known as optimization¹⁹. Various methods are available to address optimization issues. When utilizing traditional optimization techniques, the final result is typically the precise optimal value²⁰. Optimization problems are commonly solved using methods that rely on a gradient or other traditional hard computing approaches. Although the gradient technique provides an advantage, it can be time-consuming when solving problems²¹. In certain situations, particularly with nonlinear and complex issues, they may not be able to achieve a suitable outcome or fully resolve the problem²². To address this issue, traditional approaches have been supplemented with the use of metaheuristic algorithms. These methods draw inspiration from various sources, such as natural phenomena and social behaviors, and bio-inspired optimizers are among them. There are several metaheuristic algorithms available, including World Cup Optimizer (WCO)²³, Ant Lion Optimization Algorithm (ALO)²⁴, Arithmetic Optimizer (AOA)²⁵, Chimp Optimization Algorithm (COA)²⁶, Equilibrium Optimizer (EO)²⁷, Red Fox Optimization (RFO) algorithm²⁸, and Sparrow Search Algorithm (SSO)²⁹.

The Sparrow Search Optimizer is a metaheuristic algorithm that draws inspiration from the foraging behavior of sparrows, demonstrating high efficiency in solving diverse optimization challenges. Sparrows found globally, have distinct feeding preferences, with some favoring fruits and seeds while others hunt for insects or worms. They typically thrive in low-density forests and near human habitats rather than in dense woodlands. Within their groups, there are two main types: producers, who forage independently, and scroungers, who depend on others for food. Competition among scroungers leads to varying success rates. The energy dynamics in sparrow populations affect their hunting strategies, making weaker individuals more susceptible to predation. This algorithm emulates sparrow behavior to enhance solution optimization, effectively balancing exploration and exploitation, and is applicable across multiple domains.

The model of the algorithm

Like other algorithms, which are population-based, the Sparrow Search Optimizer starts with a group of randomly selected candidates²⁹. The candidate in the Sparrow Search Optimizer chooses the individual’s location, and this concept can be described as the following formula:

$$\:X=\left[\begin{array}{ccc}{x}_{\text{1,1}}&\:\cdots\:&\:{x}_{1,d}\\\:⋮&\:\ddots\:&\:⋮\\\:{x}_{n,1}&\:\cdots\:&\:{x}_{n,d}\end{array}\right]$$

(13)

Here, the number of individuals is represented by $\:n$. The decision variable’s dimension is demonstrated by $\:d$. Sparrows aim to accumulate sufficient energy reserves by searching for areas with abundant food resources. These food search zones are typically frequented by scroungers as well. The sparrows achieve their high energy stores by optimizing performance indexes based on the individuals. The performance index for the individuals is computed by the below formulation:

$$\:{F}_{X}=\left[\begin{array}{c}f\left(\left[{x}_{\text{1,1}},{x}_{\text{1,2}},\dots\:,{x}_{1,d}\right]\right)\\\:f\left(\left[{x}_{\text{2,1}},{x}_{\text{2,2}},\dots\:,{x}_{2,d}\right]\right)\\\:\begin{array}{c}⋮\\\:f\left(\left[{x}_{n,1},{x}_{n,2},\dots\:,{x}_{n,d}\right]\right)\end{array}\end{array}\right]$$

(14)

Whenever the hunters are observed, the warning signals are activated, and then the members are altered. Scroungers are directed to a safe location if the value of alarm exceeds the threshold of safety. Scrounger candidates become producers when they discover a suitable food source with more energy stores. However, the number of scroungers and makers must be maintained. Scroungers are continually looking for producers who have detected better places with more food. Additionally, some scroungers compete with producers to locate better food sources. In Sparrow Search Optimizer, an individual with a better performance index has a higher opportunity of detecting the best food source. Producers typically search a wider range of solution space, which can be defined in the following formulation:

$$\:{X}_{i,j}^{t+1}=\left\{\begin{array}{cc}{X}_{i,j}^{t}\times\:\text{exp}(-\frac{i}{\beta\:\times\:ite{r}_{max}})&\:if\:{R}_{2}<ST\\\:{X}_{i,j}^{t}+Q\times\:L&\:if\:{R}_{2}\ge\:ST\end{array}\right.$$

(15)

Here, $\:\beta\:$ represents a number that ranges from 2 to 1 and it is random. A d-dimension vector is demonstrated by $\:L$. $\:Q$ shows a value, which is randomly selected. A constant value that involves iterations’ uppermost value is illustrated by $\:ite{r}_{max}$. The value of the $\:{j}^{th}$dimension$\:\:(j=\text{1,2},\dots\:,d)$ in the $\:{i}^{th}$ individuals at iteration $\:t$ (the current iteration) is indicated by $\:{X}_{i,j}^{t}$. $\:{R}_{2}$ demonstrates the alarming signal that is a value from 0 to 1 and it is random. The range of exploration over the producer is extensive if R2 has a value less than the ST, which is considered to be between 0.5 and 1 as per the equation mentioned above. This implies that there are no hunters present at that point. The individuals recognize the hunters, and all candidates have to go to another certain place if the number of $\:{R}_{2}$ is more than $\:ST$. Some scroungers compete with the producers to go to the areas which are full of rich food sources. This motion of scroungers has been computed in the below formula:

$$\:{X}_{i,j}^{t+1}=\left\{\begin{array}{cc}Q\times\:\text{exp}\left(\frac{{X}_{worst}^{t}-{X}_{p}^{t+1}}{{i}^{2}}\right)\:\:\:\:\:\:\:\:&\:if\:i>n/2\\\:{X}_{p}^{t+1}+\left|{X}_{i,j}^{t}-{X}_{p}^{t+1}\right|\times\:{A}^{†}\times\:L&\:o.w.\end{array}\right.$$

(16)

Here, the optimum location over the producer is indicated by $\:{X}_{P}$. The present global worst situation is defined by $\:{X}_{worst}$. $\:A$ stands for a random d-dimensional vector, which is in the range of [-1,1] and $\:{A}^{†}={\text{A}}^{\text{T}}{\times\:\left(\text{A}\times\:{\text{A}}^{\text{T}}\right)}^{-1}$. The new location of the candidates after escaping the dangerous condition is computed as follows:

$$\:{X}_{i,j}^{t+1}=\left\{\begin{array}{cc}{X}_{best}^{t}+\beta\:\times\:\left|{X}_{i,j}^{t}-{X}_{best}^{t+1}\right|\:\:\:\:\:\:\:\:&\:if\:{f}_{i}>{f}_{g}\\\:{X}_{ij}^{t}+K\times\:\left(\frac{\left|{X}_{i,j}^{t}-{X}_{worst}^{t+1}\right|}{\left({f}_{i}-{f}_{w}\right)+\epsilon\:}\right)&\:{f}_{i}={f}_{g}\end{array}\right.$$

(17)

Here, there is value to keep away from the zero-division error, and it is demonstrated by ε. $\:K$ represents a random number that ranges from − 1 to 1. $\:\beta\:$ describes a distributed random amount that has a variance of 1 and a mean value of 0. The present global optimal situation is signified by $\:{X}_{best}$. The cost value of the current individual has been indicated by the current general worst value is shown by $\:{f}_{w}$, and the greatest fitness value.

Modified Sparrow Search optimizer (MSSO)

Though the real Sparrow Search Optimizer has been known as a novel and effective bio-inspired optimization algorithm, there are some restrictions in this algorithm, such as a weak exploitation and a substituting randomly, leading to a slow convergence delivery¹³. In this investigation, two methods have been introduced to modify the Sparrow Search Optimizer, including sine–cosine³⁰ and Opposition-based Learning (OBL)³¹ mechanisms in order to gain correct exploitation and exploration during the search procedure to afford a greater diversity in the population²². At first, the weakest scrounger, which indicates $\:{X}_{worst}$ (the worst solution), has been upgraded on the basis of the Sine-Cosine method, as shown in the below formula:

$$\:{X}_{worst}\left(i\right)=\left\{\begin{array}{c}{X}_{worst}\left(i\right)+{\delta\:}_{1}\times\:\text{sin}\left({\delta\:}_{2}\right)\times\:\left|{\delta\:}_{3}\times\:{X}_{Best}\left(i\right)-{G}_{worst}\left(i\right)\right|,\:{\delta\:}_{4}<0.5\:\\\:{X}_{worst}\left(i\right)+{\delta\:}_{1}\times\:\text{cos}\left({\delta\:}_{2}\right)\times\:\left|{\delta\:}_{3}\times\:{X}_{Best}\left(i\right)-{G}_{worst}\left(i\right)\right|,\:{\delta\:}_{4}\ge\:0.5\:\end{array}\right.$$

(18)

Here, the greatest solution, which is attained by the greatest producer, is defined by $\:{X}_{best}$.

$\:{X}_{best}$ defines the finest solution that is generated with the best producer and:

$$\:{\delta\:}_{1}=a-i\times\:\left(a/MI\right)$$

(19)

$$\:{\delta\:}_{2}=\left(2\times\:\pi\:\right)\times\:rand$$

(20)

$$\:{\delta\:}_{3}=2\times\:rand$$

(21)

$$\:{\delta\:}_{4}=rand$$

(22)

Here, the current iteration is represented by $\:i$. $\:rand$ demonstrates a random amount that ranges between 0 and 1. In the second iteration, 40% of the population is attained by the Opposition-based Learning Method. Based on the OBL mechanism, when the latest members of the group prepared inferior outcomes compared to their predecessors, their opposite value will be evaluated, and the superior value between the two will be selected as the new members. The Sparrow Search Algorithm’s results are improving through the use of Sine-Cosine and Opposition-based Learning Methods, which can be validated³². In this investigation, the equations provided below outline the mathematical expressions for various standard test functions, such as the Generalized Rosenbrock function, Generalized Rastrigin function, Shekel’s Foxholes, and Hartman’s Family Function. These equations will be used for analyzing and validating the effectiveness of the proposed ASSO method.

(1) The Generalized Rastrigin function:

$$\:{F}_{1}\left(x\right)={\sum\:}_{i=1}^{d}\left[{x}_{i}^{2}-10\times\:\text{cos}\left(2\times\:\pi\:\times\:{x}_{i}\right)+10\right]$$

(23)

Here, $\:-5.12\le\:{x}_{i}\le\:5.12;\:\:{F}_{1}^{min}=0;\:\:d=30$

(2) The Generalized Rosen brock function:

$$\:{F}_{2}\left(x\right)={\sum\:}_{i=1}^{d}\left[100\times\:{\left({x}_{i+1}-{x}_{i}^{2}\right)}^{2}+{\left({x}_{i}-1\right)}^{2}\right]$$

(24)

Here, $\:-30\le\:{x}_{i}\le\:30;\:\:{F}_{2}^{min}=0;\:\:d=30$

(3) The Hartman’s Family:

$$\:{F}_{3}\left(x\right)=-{\sum\:}_{i=1}^{4}{c}_{i}\times\:\text{exp}\left(-{\sum\:}_{j=1}^{d}{a}_{ij}\times\:{\left({x}_{j}-{p}_{ij}\right)}^{2}\right)$$

(25)

$$\:\text{H}\text{e}\text{r}\text{e},\:0\le\:{x}_{i}\le\:1;\:\:{F}_{3}^{min}=-3.32;\:\:d=3;\:{c}_{i}=\left[\text{1,1.2,3},3.2\right];\:{p}_{ij}=\left[\begin{array}{c}0.37\\\:0.47\\\:0.11\\\:0.40\end{array}\begin{array}{c}\:\:0.12\\\:0.44\\\:0.87\\\:0.57\end{array}\begin{array}{c}\:\:0.27\\\:0.75\\\:0.55\\\:0.88\end{array}\right]$$

(4) The Shekel’s Foxholes Function:

$$\:{F}_{4}\left(x\right)=-{\sum\:}_{i=1}^{d}{\left[\left({x}_{i}-{a}_{i}\right)\times\:{\left({x}_{i}-{a}_{i}\right)}^{T}+{c}_{i}\right]}^{-1}$$

(26)

$$\:\text{w}\text{h}\text{e}\text{r}\text{e},\:0\le\:{x}_{i}\le\:10;\:\:{F}_{4}^{min}=-10.1532;\:\:d=4;\:{c}_{i}=\left[\text{0.1,0.2,0.2,0.4}\right];\:{a}_{i}=[\text{4,1},\text{8,6}]$$

After that, the accomplishments of the optimizer were compared to some of the latest bio-inspired methods, such as Spotted Hyena Optimizer (SHO)³³, Locust Search (LS)³⁴, and the standard Sparrow Search Optimizer²⁹ to illustrate its greater accuracy. To provide consistent and reliable accomplishments, every function of benchmark was tested thirty times in an independent way using all available optimizers. The comparison process was made more fair by using a maximum iteration value of 200 and a population number of 120 for all tests. Table 2 displays the simulation results of the analyzed metaheuristics using four measurement indicators. These indicators include the maximum amount (max), the minimum amount (min), mean value, and value of Std. The simulations were conducted in MATLAB R2017b environment on a 64-bit Core i-7 PC with Windows ten and sixteen GB RAM. It’s worth noting that the four statistical measures are all related to the data set being analyzed.

Table 2 Optimization algorithm performance estimation by the objective functions.

Based on Table 2, the proposed Amended Sparrow Search Optimizer approach provides better accuracy for the minimum, maximum, and average amounts for each function. Additionally, the fact that the standard deviation value is the lowest indicates that the suggested Amended Sparrow Search Optimizer approach is more reliable during independent runs.

Combined DBN/MSSO

The hybrid approach marries the Deep Belief Network (DBN) with the Modified Sparrow Search Optimizer (MSSO) algorithm to enhance network learning. While the Backpropagation (BP) technique underpins the algorithm, it has limitations—it can confine the algorithm to a narrow solution space, which may compromise pattern identification accuracy. To circumvent these drawbacks, the MSSO optimization methodology is employed, aiming to mitigate the effect of local minimums and enhance the optimization process.

(1) DBN Weight Optimization is achieved via the MSSO algorithm.

When using MSSO in DBN, selecting the appropriate fitness function and figuring out the search criteria are two crucial things to keep in mind.

So, MSSO -based DBN may be configured as follows:

(2) Estimate the fitness value per DBN / MSSO based on the main whales’ number that has N weight.

(3) Upgrade the prey blockage and efficiency of the position for fitness value on the basis of feeding pure bubble.

(4) The whale algorithm should be applied to every agent using alternative operators.

(5) Ensure that the network has attained acceptable rates of error or fulfilled the necessary criterion.

(6) Move to (2) if the criteria condition is not defined.

(7) After fulfilling the requirement of the criteria:

(8) End.

The error of DBN is estimated using MSE as a performance index. MSE evaluates the variation between actual values, as well as the optimum values every training instance.

The formulation of MSE is defined as follows:

$$\:MSE=\frac{1}{n}\:{\sum\:_{i=1}^{n}\sum\:_{j=1}^{m}\left({y}_{j}\left(k\right)-{y}_{j}^{*}\left(k\right)\right)}^{2}$$

(27)

Here, the actual amount is represented by $\:y$. The stage’s quantity in the training set of data is demonstrated by $\:n$.

Here, the goal is to make a reliable and optimized approach of neural network for runoff forecasting utilizing DBN / MSSO.

Optimal SWAT model

The Soil and Water Assessment Tool (SWAT) model is a comprehensive simulator used to predict the impact of land management practices on water resources by modeling the hydrological cycle. The original SWAT model’s accuracy depends on input data quality, model parameters, and calibration and validation procedures. To enhance its performance, an optimized version, the optimal SWAT system, has been developed through calibration and validation, improving its accuracy in simulating hydrological processes, particularly runoff prediction. This optimized model offers increased precision in hydrological forecasts, aiding decision-makers in water resource management. It also reduces uncertainty, making it a more reliable tool for long-term planning. Optimization algorithms, such as metaheuristic optimization, have been applied to further enhance the SWAT model’s accuracy, making it a valuable tool for hydrological studies and water management. This research combines the SWAT model with a Deep Belief Network and optimizes it using the MSSO optimization method, improving runoff forecast accuracy and reducing calibration time. The optimum SWAT model for prediction of runoff is represented in Fig. (3).

Fig. 3

The proposed SWAT-DBN-MSSO’s overall block diagram.

Applicability evaluation of models

In this study, the efficacy of the model was evaluated utilizing the Nash-Sutcliffe coefficient (ENS), Mean Square Error (MSE), and coefficient of determination (R²).

The coefficient of determination (R²) is a metric used to assess the temporal correlation between model simulations and observed data, with values ranging from 0 to 1. A higher R² value, closer to 1, indicates better model accuracy and performance.

The Nash-Sutcliffe coefficient (ENS) evaluates the predictive capacity of a hydrological model, ranging from -infinity to 1. An ENS value less than 0 indicates a poorer prediction than the observed mean, while a value of 0 represents equal accuracy between the model and observed data.

The Mean Square Error (MSE) measures the average squared deviation between predicted and actual values, with lower MSE values indicating superior predictive accuracy. For a hydrological model to be considered successful, it should aim for an ENS value greater than 0.5, an R² value closer to 1, and an MSE value approaching zero, ensuring accurate and reliable simulations.

The Persistence Index (PI) is widely recognized as a standard benchmarking technique. It assesses the ratio of the residual variance, often referred to as noise, to the variance of the errors derived from a basic persistence model. An ideal PI value is 1.0, with values exceeding 0.0 signifying a minimally acceptable level of performance.

Volumetric Efficiency (VE) acts as a critical indicator for evaluating the precision of runoff volume forecasts generated by a model. When VE values exceed 100%, it signifies an overestimation, where the model anticipates a greater volume of runoff than what is actually recorded. VE values ranging from 100 to 0% reflect varying levels of underestimation, with lower values denoting a more pronounced divergence from the actual data. Ideally, VE values should hover around 100%, indicating that the model’s runoff volume predictions are accurate. Conversely, VE values falling below 0% represent pessimistic runoff predictions, which lack physical relevance and highlight a substantial inconsistency between the model’s forecasts and the observed outcomes³⁵.

The following are the formulae for ENS, R², and MSE. Table 3. illustrates the metrics utilized to evaluate models.

Table 3 The metrics utilized to evaluate models.

Results

Evaluation of the reliability of the climate models

A downscaled dataset consisting of 5 CMIP6 models has been employed to evaluate the performance of simulations datasets in comparison with base time datasets. Figure 4 shows the PSL-CM6A-LR model satisfactory correlation between the simulated and observed rainfall (A) and temperature (B) values.

Fig. 4

PSL-CM6A-LR model satisfactory correlation between the simulated and observed rainfall (A) and temperature (B) values.

The correlation coefficients for simulated versus observed rainfall (0.80) and temperature (0.71) suggest that the PSL-CM6A-LR model effectively captures the climatic features of the study area. This analysis of correlation enhances confidence in the model’s capacity to simulate climate scenarios and their possible effects on hydrological processes, which is crucial for evaluating water resource dynamics in the region.

Meteorological information prediction

Figure 5 presents the assessment of temperature and precipitation variations data within the context of the SSP1(A) and SSP5(B) scenarios.

Fig. 5

Temperature (A) and Precipitation (B) monthly values forecasting.

The simulation outcomes of the SSP1 (optimistic) and SSP5 (pessimistic) scenarios evince an advance in the mean monthly temperature compared to the reference interval. The alterations are particularly conspicuous within the SSP5 scenario, which postulates more adverse socio-economic circumstances than the present era. The potential ramifications of escalating temperatures include significant repercussions on ecosystems and an augmented susceptibility to devastating seasonal floods. Based on the simulation results, it is evident that the maximum temperature is recorded during August and July. The shift in peak temperatures could impact the quantity of runoff produced. Furthermore, the research discloses a decline in the average annual rainfall over the projected timeframe for both scenarios. However, it is crucial to acknowledge that this decline is not uniformly distributed throughout the year. Notably, there is a substantial reduction in precipitation levels that may be observed in the spring and summer months, specifically in May and June. Figure 6 shows the temperature and precipitation changes from 2023 to 2100 under SSPs, respectively.

Fig. 6

Average temperature and precipitation changes under SSPs.

On the basis of the outcomes obtained, it has been determined that the mean annual temperature, relative to the reference period of 2000–2023 with an average of approximately 23.42 ℃. It is predicted that SSP1 and SSP5 will increase by 0.243% and 0.319% per decade, respectively. As a result, by the year 2100, the average annual temperature will reach 2.55 ℃ in the optimistic case and in the pessimistic case will reach 1.94 ℃. The range of temperature changes will be between 1.94 ℃and 2.55 ℃.

Furthermore, the findings indicate that compared to the reference period, where the average annual rainfall was approximately 665.56 mm, it is projected to decrease to around 26.02. and 48.42 mm per decade under SSP1 and SSP5 by 2100. The results show warming and drought in the Jinsha River under optimistic and pessimistic scenarios.

The downscaled climate datasets, derived from the PSL-CM6A-LR model under SSP1 and SSP5, offer access to meteorological variables such as precipitation and temperature. The utilization of these datasets is of paramount importance in facilitating the implementation of the SWAT model, a computational tool designed to simulate the intricate hydrological processes associated with the creation of runoff. Precipitation data determine the rainfall distribution, while temperature data influences evapotranspiration rates, soil moisture conditions, and snowmelt dynamics. Integrating downscaled climate information into the SWAT model framework makes it possible to replicate hydrological processes and assess the influences of climatic changes and change on the resources of water at a regional level. In the subsequent section, the production runoff has been assessed utilizing the proposed SWAT model.

Evaluation of the reliability of the optimized SWAT model

This section focuses on simulating runoff using combined SWAT-DBN-MSSO models. Figure 7. show the simulation of runoff by combined SWAT model with DBN model by type of different optimization algorithm.

Fig. 7

The simulation of runoff by optimized DBN-SWAT model.

The DBN-SWAT hybrid model, in collaboration with the MSSO optimizer, has shown significant enhancements in simulation accuracy through careful calibration of parameter values and configurations to match observed data better. The results of the simulations demonstrate a closer alignment with actual values, highlighting the hybrid model’s enhanced capability to represent complex hydrological processes and their interactions. The optimizer effectively explores the parameter space to determine optimal parameter sets, thereby improving the model’s ability to mirror real-world phenomena. This increased alignment between simulated and observed values indicates a more robust instrument for understanding and predicting runoff dynamics.

As demonstrated in Table 4, the assessment metrics shows that the Soil and Water Assessment Tool system’s capability to simulate monthly streamflow at the Panzhihua hydrological station is considered acceptable according to the established criteria. The ENS value attained was 0.7152, the R² value was 0.8012, the MSE value was 0.2145, the VI value is about 69%, and PI is about 0.71.

Table 4 Results of the SWAT model’s ability.

The runoff prediction by optimized SWAT model

According to finding in Sect. 3.2 the optimized SWAT model based on DBN/MSSO method the runoff forecasting by this model. The Fig. 8 shows the annual runoff forecasting for 2023 to 2100.

Fig. 8

Annual runoff forecasting.

Based on the research results, it is projected that there will be a significant decrease in the amount of runoff in the following years. The drop in runoff may be principally ascribed to two critical factors: a discernible decline in precipitation and a concomitant rise in temperature. These circumstances signify an imminent water shortage, harming multiple sectors, including providing potable water and agricultural endeavors. Hence, using the data acquired from these circumstances to provide a holistic approach to water resource management is crucial. The anticipated alterations in precipitation and temperature patterns will directly impact the total runoff within the area. Due to reduced levels of precipitation and elevated temperatures, a substantial quantity of water has the potential to undergo evaporation, resulting in a decline in the amount of runoff. As a result, the anticipated decrease in runoff quantities indicates a diminished supply of water entering rivers, lakes, or reservoirs. The current circumstances need the adoption of comprehensive policies for managing water resources to tackle the impending issue of water shortage successfully. Efforts should be directed towards developing strategies to exploit existing water resources efficiently, emphasizing meeting drinking water needs and supporting agricultural endeavors. This may include implementing water conservation strategies, using modern water-saving technology, and investigating alternate water sources, such as groundwater or recycled water.

Conclusion

This research shows that climate change has a profound effect on hydrological processes, especially in relation to runoff. This study used the CMIP6 model to predict climate variables affecting runoff in different social and economic directions. In addition, a deep belief network (DBN) and a modified sparrow search optimizer (MSSO) were used to enhance the runoff prediction capabilities of the SWAT model. DBN is adept at recognizing complex data patterns, thereby improving the accuracy of runoff forecasting. The results show that the PSL-CM6A-LR model acts as an effective tool for predicting climate variables. The findings project temperature increases under different scenarios, with mean annual temperatures projected to increase between 0.243% and 0.319% per decade, ultimately reaching an estimated range of 1.94℃ to 2.55℃ by 2100. These temperature changes are expected to have significant consequences for the hydrological dynamics and water resources of the basin, emphasizing the critical need for adaptation and mitigation strategies in response to climate change in the region. In addition, the research shows a projected decrease in annual precipitation in the study area, with simulations showing a decrease of 26.02 mm to 48.42 mm per decade by 2100 compared to the reference period. The performance evaluation of the SWAT model shows a satisfactory simulation of the monthly flow, which shows the optimal model with an ENS score of 0.7152 and a coefficient of determination R² of 0.8012. The study also predicts a significant decrease in runoff as a result of the projected decrease in precipitation and increase in temperature, highlighting the urgent need for comprehensive water resources management policies.