Introduction

Nonlinear phenomena play a crucial role in various research fields. Nonlinear partial differential equations (NPDEs) can describe nonlinear phenomena, and their fundamental properties are studied through solitonic solutions observed in diverse areas such as plasmas physics, fluid dynamics, bio-science, solid state, and electrical circuits, among others1,2,3,4,5,6. The study of solitons has been of great interest to many researchers, and several features of solitary wave solutions have been associated with them. For instance, Feng and Hou observed the first soliton in a mono-pulse water wave7. Zhang, Lin, and Liu8, Wazwaz9, Rustam, Saha, Chatterjee10, and Abdelsalam11 have discovered numerous solitonic solutions in their research.

Various effective methods like the Bäcklund transformation, exp-function method, and extended tanh-function schemes have emerged from advancements in soliton theory12,13,14,15,16,17,18. In addition, stochastic soliton of stochastic nonlinear models are profoundly examined by ongoing youthful researchers to decreasing erratic vacillations of wave’s amplitudes. It is as yet neglected the stochastic wave arrangement following every energy circles of stage representations from Hamiltonian of the model. Methods like tanh-coth, multiple exp-function, modified simple equation, Darboux transformation, and higher-order Runge-Kutta, among others, have been developed in soliton theory19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35.

The fractional derivatives field has been a concern in many sciences and engineering research fields. Recently, fractional order derivatives have been used in diverse real-life models of science and technology36,37,38,39,40,41,42,43,44. Consequently, it is a wonder why many researchers in fractional calculus have dedicated their devotion to recommending new fractional order derivatives45,46,47,48,49,50,51.

In concentrating on the parametric wave condition in a Kerr medium, Baronio52used the one-layered dissipating limit while considering bunch speed scattering and time-subordinate space-time that needed aspects. For the purpose of modeling light propagation through a medium, the ray equation, also referred to as the paraxial wave equation, provides a simplified representation of the entire wave equation53. To investigate some optical solutions to the truncated time M-fractional paraxial wave equation, we employ the modified, extended auxiliary mapping technique54to examine the truncated time M-fractional derivative55:

$$\:i\frac{\partial\:P}{\partial\:z}+\frac{{a}_{1}}{2}{}_{\kappa\:}{}^{\:}{D}_{M,t}^{2\sigma\:,\varphi\:}\:P+\frac{{a}_{2}}{2}\:\frac{{\partial\:}^{2}P}{\partial\:{y}^{2}}-{a}_{3}{\left|P\right|}^{2}P=0,$$
(1)

where \(\:{a}_{1},{a}_{2},\) and \(\:{a}_{3}\) are real constants, \(\:{a}_{1}\) is the dispersal effect, \(\:{a}_{3}\) is the Kerr non-linearity effect, and \(\:{a}_{2}\) is the diffraction effect. The M-fractional derivative is \(\:{}_{\kappa\:}{}^{\:}{D}_{M,t}^{2\sigma\:,\varphi\:}\), and the longitudinal, transverse, and temporal propagation are denoted by the variables \(\:z,y\), and \(\:t\), respectively.

The primary point of this exploration is to research the new optical wave answers for the shortened M-fractional derivative paraxial model along with complete non-linearity with the assistance of the modified extended auxiliary mapping method. The inspiration for this paper is that an interesting M-fractional derivative is utilized for our concerned paraxial model, which is my insight. The significance of the M-fractional derivative is that it satisfies both the properties of integer and partial request subsidiaries. The impact of fractional order derivative on the got arrangements is likewise made sense graphically. Counting a partial request term in the paraxial wave condition prompts the rise of new optical solitons, making it a really engaging option in contrast to the ordinary number request paraxial wave condition.

The following sections make up this work: The M-truncated fractional derivative is discussed in Sect. "M-truncated fractional derivative". In Area 3, the functioning strategy of the altered broadened assistant planning procedure is edified. In Area 4, we carried out the changed expanded helper planning procedure into the M-shortened partial paraxial wave condition. The numerical simulations and graphical representations of some of the obtained results are discussed in Sect. "Result and discussions". The comparisons are made to a recently published article in Sect. "Comparisons". At last, the paper closes with a synopsis of its discoveries.

M-truncated fractional derivative

Oliveira and Sousa proposed the M-truncated fractional derivative as a brand-new variant of the M-fractional derivative56,57. The M-truncated fractional derivative is a more adaptable alternative because it eliminates the limitations of conventional derivatives.

Definition

Given a function and an order, the M-truncated fractional derivative is defined as follows

$$\:{{}_{\kappa\:}{}^{\:}{D}_{M,t}^{\sigma\:,\varphi\:}u\left(t\right)}^{\:}=\underset{\epsilon\to\:0}{\text{lim}}\frac{u\left({t\:}_{\kappa\:}{E}_{\varphi\:}\left(\epsilon{t}^{-\sigma\:}\right)\right)-u\left(t\right)}{\epsilon},\:t>0,\varphi\:>0.$$

Here, \(\:{\:}_{\kappa\:}{E}_{\varphi\:}\left(x\right)\:\)is a truncated Mittag-Leffler function of one parameter, defined as57, and taking values in the interval \(\:\left(\text{0,1}\right)\)

$$\:{\:}_{\kappa\:}{E}_{\varphi\:}\left(x\right)={\sum\:}_{n=0}^{\kappa\:}\frac{{x}^{n}}{\varGamma\:\left(\varphi\:n\:+\:1\right)}.$$

Characteristics

Suppose that \(\:0<\sigma\:<1,\) and\(\:\:\:l,\:m\mathfrak{\:}\in\:\mathfrak{\:}\mathfrak{R}\). Let \(\:u,\:v\)be functions that are \(\:\sigma\:\)-differentiable at a point\(\:\:n>\:0\). Then,

$$\:{1.}\quad_{\kappa\:}{}^{\:}{D}_{M,t}^{\sigma\:,\varphi\:}\left(lu+mv\right)=l{}_{\kappa\:}{}^{\:}{D}_{M,t}^{\sigma\:,\varphi\:}\left(u\right)+m{}_{\kappa\:}{}^{\:}{D}_{M,t}^{\sigma\:,\varphi\:}\left(v\right),$$
(Distribution law)
$$\:{2.}\quad\quad\quad_{\kappa\:}{}^{\:}{D}_{M,t}^{\sigma\:,\varphi\:}\left(uv\right)=u{}_{\kappa\:}{}^{\:}{D}_{M,t}^{\sigma\:,\varphi\:}\left(v\right)+v{}_{\kappa\:}{}^{\:}{D}_{M,t}^{\sigma\:,\varphi\:}\left(u\right),$$
(Multiplication law)
$$\:{3.}\quad\quad\quad\quad\quad\quad_{\kappa\:}{}^{\:}{D}_{M,t}^{\sigma\:,\varphi\:}\left(\frac{u}{v}\right)=\frac{v{}_{\kappa\:}{}^{\:}{D}_{M,t}^{\sigma\:,\varphi\:}\left(u\right)-u{}_{\kappa\:}{}^{\:}{D}_{M,t}^{\sigma\:,\varphi\:}\left(v\right)}{{v}^{2}},$$
(Divide law)
$$\:{4.}\quad\quad\quad\quad\quad\quad\quad_{\kappa\:}{}^{\:}{D}_{M,t}^{\sigma\:,\varphi\:}\left({t}^{\chi\:}\right)=\varphi\:{t}^{\chi\:-\sigma\:},\:\varphi\:\in\:\mathfrak{R},$$
(Power rule)
$$\:{5.}\quad\quad\quad\quad\quad\quad\quad\quad\quad_{\kappa\:}{}^{\:}{D}_{M,t}^{\sigma\:,\varphi\:}\left(c\right)=0\:,\:\:c\in\:\mathfrak{R}$$
(Constant law)

If \(\:u\), is differentiable at 

$$\:6.\quad\quad\quad{}_{\kappa\:}{}^{\:}{D}_{M,t}^{\sigma\:,\varphi\:}\left(u\circ\:v\right)\left(t\right)={u}^{{\prime\:}}\left(v\right){}_{\kappa\:}{}^{\:}{D}_{M,t}^{\sigma\:,\varphi\:}v\left(t\right).$$

If u, is differentiable

$$\:7.\quad\quad\quad\quad{}_{\kappa\:}{}^{\:}{D}_{M,t}^{\sigma\:,\varphi\:}u\left(t\right)=\frac{{t}^{1-\sigma\:}}{{\Gamma\:}\left(\varphi\:+1\right)\:}\frac{du}{dt}.\:$$

Remarks Assuming that \(\:u\) is a \(\:\sigma\:\)-differentiable in the interval \(\:\left(0,p\right),\) where\(\:\:\:p>0,\) then the following holds.

$$\:{}_{\kappa\:}{}^{\:}{D}_{M,t}^{\sigma\:,\varphi\:}u\left(0\right)=\underset{t\to\:{0}^{+}}{\text{lim}}\left({}_{\kappa\:}{}^{\:}{D}_{M,t}^{\sigma\:,\varphi\:}u\left(t\right)\right).$$

A brief description of modified extended auxiliary mapping technique

The nonlinear equation is expressed in terms of the M-truncated fractional derivative as follows58.

$$\:F\left(P,{}_{\kappa\:}{}^{\:}{D}_{M,t}^{\sigma\:,\varphi\:}P,{}_{\kappa\:}{}^{\:}{D}_{M,t}^{2\sigma\:,\varphi\:}P,{}_{\kappa\:}{}^{\:}{D}_{M,y}^{2\sigma\:,\varphi\:}P,\dots\:\right)=0.$$
(2)

Step 1:

Suppose the following transformation

$$\:\phi\:={l}_{1}y+{l}_{2}z+\frac{\varGamma\:\left(\varphi\:+1\right)}{\sigma\:}\left(\omega\:{t}^{\sigma\:}\right),\:\:\xi\:={v}_{1}y+{v}_{2}z+\frac{\varGamma\:\left(\varphi\:+1\right)}{\sigma\:}\left(\tau\:{t}^{\sigma\:}\right)+\delta\:,\:\:P\left(y,z,t\right)=Q\left(\phi\:\right)\:{e}^{i\xi\:}.$$
(3)

The ordinary differential equation is derived from the given equation by utilizing the above transformation in Eq. (2) :

$$\:F\left(Q,\omega\:{Q}^{{\prime\:}},{\omega\:}^{2}{Q}^{{\prime\:}{\prime\:}},{{l}_{1}}^{2}{Q}^{{\prime\:}{\prime\:}{\prime\:}},\:\dots\:\right)=0.$$
(4)

Step 2:

According to the Modified extended auxiliary mapping technique, the exact solution of Eq. (4) is assumed to be,

$$\:Q=\sum\:_{j=0}^{n}{\mathcal{A}}_{j}{S}^{j}+\sum\:_{j=-1}^{-n}{\mathcal{B}}_{-j}{S}^{j}+\sum\:_{j=2}^{n}{\mathcal{C}}_{j}{S}^{j-2}{S}^{{\prime\:}}+\sum\:_{j=1}^{n}{\mathcal{D}}_{j}{\left(\frac{{S}^{{\prime\:}}}{S}\right)}^{j}.$$
(5)

Where, the coefficient \(\:{\mathcal{A}}_{j},{\mathcal{B}}_{-j},\:\:{\mathcal{C}}_{j}\) and \(\:{\mathcal{D}}_{j}\)are to be calculate later and \(\:n\) is obtained by homogeneous balance with higher derivative and non-linear term. Here \(\:S\left(\phi\:\:\right)\) satisfies the following auxiliary ordinary differential equation:

$$\:{\text{S}}^{{\prime\:}}\left(\phi\:\right)=\sqrt{{{\upbeta\:}}_{1}{\text{S}}^{2}+{{\upbeta\:}}_{2}{\text{S}}^{3}+{{\upbeta\:}}_{3}{\text{S}}^{4}},$$
(6)

where \(\:{\beta\:}_{1},{\beta\:}_{2}\:\)and \(\:{\beta\:}_{3}\) are real constants. The Eq. (6) admits the following solutions.

Case-01:

$$\:S\left(\phi\:\right)=-\frac{{\beta\:}_{1}\left(\epsilon\times\:{coth}\left(\frac{1}{2}\sqrt{{\beta\:}_{1}}\left(\phi\:+{\phi\:}_{0}\right)\right)+1\right)\:\:\:\:}{{\beta\:}_{2}},$$
(7)
$$\:\text{w}\text{h}\text{e}\text{r}\text{e}\:\epsilon=1\:\text{o}\text{r}-1,\:\text{a}\text{n}\text{d}\:{\beta\:}_{2}^{2}-4{\beta\:}_{1}{\beta\:}_{3}=0.$$

Case-02:

$$\:S\left(\phi\:\right)=-\sqrt{\frac{{\beta\:}_{1}}{4{\beta\:}_{3}}}\times\:\left(\frac{{\beta\:}_{1}\left(\epsilon\times\:{sinh}\left(\sqrt{{\beta\:}_{1}}\left(\phi\:+{\phi\:}_{0}\right)\:\right)\right)}{{cosh}\left(\sqrt{{\beta\:}_{1}}\left(\phi\:+{\phi\:}_{0}\right)\right)+\eta\:\:}+1\right),$$
(8)
$$\:\text{w}\text{h}\text{e}\text{r}\text{e},\:{\left(\epsilon,\eta\:\right)=\left(\pm\:1,\pm\:1\right),\beta\:}_{1}>0,\:\:\:{\beta\:}_{3}>0,\:\:\text{a}\text{n}\text{d}\:{\beta\:}_{2}=2\sqrt{{\beta\:}_{1}{\beta\:}_{3}}.$$

Case-03:

$$\:S\left(\phi\:\right)=-\frac{{\beta\:}_{1}\left(\frac{\epsilon\times\:{sinh}\left(\sqrt{{\beta\:}_{1}}\left(\phi\:+{\phi\:}_{0}\right)\:\right)+\rho\:\:\:\:\:}{{cosh}\left(\sqrt{{\beta\:}_{1}}\left(\phi\:+{\phi\:}_{0}\right)\right)+\eta\:\:\sqrt{{\rho\:}^{2}+1}}+1\right)}{{\beta\:}_{2}},$$
(9)

where, \(\:{\left(\epsilon,\eta\:\right)=\left(\pm\:1,\pm\:1\right),\:\:\beta\:}_{1}>0.\)  

Step-3. Concerning the transformation of Eq. (5) into Eq. (4) and by combining all of the similar orders of \(\:{S{\prime\:}}^{k}\left(\phi\:\right)\:{S}^{j}\left(\phi\:\right)\)\(\:(k=\text{0,1};j=\text{0,1}\dots\:.n)\). By setting then to zero we obtain a collection of algebraic systems.

Step-4. Solving the algebraic equations by use of Maple we evaluate the value of the constants \(\:{\mathcal{A}}_{j},{\mathcal{B}}_{-j},\:\:{\mathcal{C}}_{j}\) and\(\:\:{\mathcal{D}}_{j}\). Supplanting the approximations of the constants organized with the preparations of equivalence of Eq. (6) into Eq. (5), we will get new and extensive exact voyaging wave courses of action of the nonlinear advancement of Eq. (2).

Formation of optical solitons of paraxial wave equation

The fractional part of the paraxial wave equation has a significant effect on the shape of the pulse, as illustrated by the following. \(\:P\left(y,z,t\right)=Q\left(\phi\:\right){e}^{i\xi\:}\) in Eq. (1) becomes

$$\:\phi\:={l}_{1}y+{l}_{2}z+\frac{\varGamma\:\left(\varphi\:+1\right)}{\sigma\:}\left(\omega\:{t}^{\sigma\:}\right),\:\:\xi\:={v}_{1}y+{v}_{2}z+\frac{\varGamma\:\left(\varphi\:+1\right)}{\sigma\:}\left(\tau\:{t}^{\sigma\:}\right)+\delta.$$
(10)

By applying the transformation given in Eq. (5) to Eq. (1) and then separating the resulting expression into its imaginary and real parts, we arrive at the following.

$$\:\left({a}_{1}{\omega\:}^{2}+{a}_{2}{l}_{1}^{2}\right){Q}^{{\prime\:}{\prime\:}}\left(\phi\:\:\right)-\left({a}_{1}{\tau\:}^{2}+{a}_{2}{v}_{1}^{2}+2{v}_{2}\right)Q\left(\phi\:\right)-2{a}_{3}{Q}^{3}\left(\phi\:\right)=0,$$
(11)

and

$$\:\left(2{a}_{1}\tau\:\omega\:+2{a}_{2}{l}_{1}{v}_{1}+2{l}_{2}\right){Q}^{{\prime\:}}\left(\phi\:\right)=0.$$

As \(\:{Q}^{{\prime\:}}\left(\phi\:\right)\ne\:0\)

$$\:{l}_{2}=-\left({a}_{1}\tau\:\omega\:+{a}_{2}{l}_{1}{v}_{1}\right).$$
(12)

Applying the homogeneous balancing rule on Eq. (11), we get \(\:\text{n}=1\).

$$\:Q\left(\phi\:\right)=\:{\mathcal{A}}_{0}+{\mathcal{A}}_{1}S+\frac{{\mathcal{B}}_{1}}{S}+\frac{{D}_{1}{S}^{{\prime\:}}}{S}.$$
(13)

Substituting Eq. (13) with Eq. (6) into Eq. (11), we obtain a polynomial \(\:{S{\prime\:}}^{k}\left(\phi\:\right)\:{S}^{j}\left(\phi\:\right)\)\(\:(k=\text{0,1};j=\text{0,1}\dots\:.n)\:\) and setting the coefficients of this polynomial equal to zero leads to the following.

$$\:{\varvec{S}}^{0}\left(\varvec{\phi\:}\right){\left[{\varvec{S}}^{\mathbf{{\prime\:}}}\left(\varvec{\phi\:}\right)\right]}^{0}:-4{a}_{3}{A}_{0}^{3}+\left(-12{D}_{1}^{2}{a}_{3}{\beta\:}_{1}-2{\tau\:}^{2}{a}_{1}-24{A}_{1}{B}_{1}{a}_{3}-2{a}_{2}{v}_{1}^{2}-4{v}_{2}\right){A}_{0}+{\beta\:}_{2}{B}_{1}\left({\omega\:}^{2}{a}_{1}-12{D}_{1}^{2}{a}_{3}+{a}_{2}{l}_{1}^{2}\right)=0,$$
$$\:{\varvec{S}}^{1}\left(\varvec{\phi\:}\right):\left(-6{a}_{3}{A}_{1}^{2}{B}_{1}+\left(\left(-6{D}_{1}^{2}{\beta\:}_{1}-6{A}_{0}^{2}\right){a}_{3}+\left({\omega\:}^{2}{a}_{1}+{a}_{2}{l}_{1}^{2}\right){\beta\:}_{1}-{\tau\:}^{2}{a}_{1}-{a}_{2}{v}_{1}^{2}-2{v}_{2}\right){A}_{1}-6{D}_{1}^{2}{a}_{3}\left({A}_{0}{\beta\:}_{2}+{B}_{1}{\beta\:}_{3}\right)\right)=0,$$
$$\:{\varvec{S}}^{2}\left(\varvec{\phi\:}\right):-12{a}_{3}{A}_{0}{A}_{1}^{2}+3{\beta\:}_{2}\left({\omega\:}^{2}{a}_{1}-4{D}_{1}^{2}{a}_{3}+{a}_{2}{1}_{1}^{2}\right){A}_{1}-12{a}_{3}{A}_{0}{D}_{1}^{2}{\beta\:}_{3}=0,$$
$$\:{\varvec{S}}^{-1}\left(\varvec{\phi\:}\right){\varvec{S}}^{\mathbf{{\prime\:}}}\left(\varvec{\phi\:}\right):-{D}_{1}\left(\left(2{D}_{1}^{2}{\beta\:}_{1}+6{A}_{0}^{2}+12{A}_{1}{B}_{1}\right){a}_{3}+{\tau\:}^{2}{a}_{1}+{a}_{2}{v}_{1}^{2}+2{v}_{2}\right)=0,$$
$$\:{\varvec{S}}^{3}\left(\varvec{\phi\:}\right):2{A}_{1}\left(\left({\omega\:}^{2}{a}_{1}-3{D}_{1}^{2}{a}_{3}+{a}_{2}{l}_{1}^{2}\right){\beta\:}_{3}-{A}_{1}^{2}{a}_{3}\right)=0,$$
$$\:{\varvec{S}}^{-2}\left(\varvec{\phi\:}\right):-6{a}_{3}{A}_{0}{B}_{1}^{2}=0,$$
$$\:{\varvec{S}}^{-1}\left(\varvec{\phi\:}\right):-\left(\left(6{D}_{1}^{2}{\beta\:}_{1}+6{A}_{0}^{2}+6{A}_{1}{B}_{1}\right){a}_{3}+\left(-{\omega\:}^{2}{a}_{1}-{a}_{2}{l}_{1}^{2}\right){\beta\:}_{1}+{\tau\:}^{2}{a}_{1}+{a}_{2}{v}_{1}^{2}+2{v}_{2}\right){B}_{1}=0,$$
$$\:{\varvec{S}}^{\mathbf{{\prime\:}}}\left(\varvec{\phi\:}\right):{D}_{1}\left({\beta\:}_{2}\left({\omega\:}^{2}{a}_{1}-4{D}_{1}^{2}{a}_{3}+{a}_{2}{l}_{1}^{2}\right)-24{a}_{3}{A}_{0}{A}_{1}\right)=0,$$
$$\:{\varvec{S}}^{-3}\left(\varvec{\phi\:}\right):-2{a}_{3}{B}_{1}^{3}=0,$$
$$\:{\varvec{S}}^{\mathbf{{\prime\:}}}\left(\varvec{\phi\:}\right)\varvec{S}\left(\varvec{\phi\:}\right):2\left(\left({\omega\:}^{2}{a}_{1}-{D}_{1}^{2}{a}_{3}+{a}_{2}{l}_{1}^{2}\right){\beta\:}_{3}-3{A}_{1}^{2}{a}_{3}\right){D}_{1}=0,$$
$$\:{\varvec{S}}^{-2}\left(\varvec{\phi\:}\right){\varvec{S}}^{\mathbf{{\prime\:}}}\left(\varvec{\phi\:}\right):-12{a}_{3}{A}_{0}{B}_{1}{D}_{1}=0,$$
$$\:{\varvec{S}}^{-3}\left(\varvec{\phi\:}\right){\varvec{S}}^{\mathbf{{\prime\:}}}\left(\varvec{\phi\:}\right):-6{a}_{3}{B}_{1}^{2}{D}_{1}=0.$$

Solving the aforementioned system of equations yields the following solution:

$$\:\omega\:=\pm\:\sqrt{-\frac{{a}_{2}{\beta\:}_{1}{l}_{1}^{2}+2{a}_{1}{\tau\:}^{2}+2{a}_{2}{v}_{1}^{2}+4{v}_{2}}{{a}_{1}{\beta\:}_{1}}},{\mathcal{A}}_{0}=0,\:{\mathcal{B}}_{1}=0,{\mathcal{A}}_{1}=\pm\:\sqrt{-\frac{{a}_{1}{\tau\:}^{2}{\beta\:}_{3}+{a}_{2}{\beta\:}_{3}{v}_{1}^{2}+2{\beta\:}_{3}{v}_{2}}{2{a}_{3}{\beta\:}_{1}}},{\mathcal{D}}_{1}=\pm\:\sqrt{-\frac{{a}_{1}{\tau\:}^{2}+{a}_{2}{v}_{1}^{2}+2{v}_{2}}{2{a}_{3}{\beta\:}_{1}}},$$
(14)

Case 01

when β1>0, E=-1 or 1 and β22-4β1 β3 = 0 then

$$\:{P}_{\text{1,2}}^{\:}\left(y,z,t\right)=\left(M\pm\:N\right)\:{e}^{i\xi\:}\:\text{a}\text{n}\text{d}\:\:{P}_{\text{3,4}}^{\:}\left(y,z,t\right)=\left(-M\pm\:N\right)\:{e}^{i\xi\:},$$
(15)

Where, \(\:M=\frac{\sqrt{-\frac{2\left({a}_{1}{\tau\:}^{2}{\beta\:}_{3}+{a}_{2}{\beta\:}_{3}{v}_{1}^{2}+2{\beta\:}_{3}{v}_{2}\right)}{{a}_{3}{\beta\:}_{1}}}\hspace{0.17em}{\beta\:}_{1}\left(\epsilon\text{coth}\left(\frac{\sqrt{{\beta\:}_{1}}\hspace{0.17em}\left(\phi\:+{\phi\:}_{0}\right)}{2}\right)+1\right)}{2{\beta\:}_{2}},\)

$$\:N=\frac{\sqrt{-\frac{2\left({a}_{1}{\tau\:}^{2}+{v}_{1}^{2}{a}_{2}+2{v}_{2}\right)}{{a}_{3}{\beta\:}_{1}}}\hspace{0.17em}\sqrt{{\beta\:}_{1}}\hspace{0.17em}\epsilon\left(1-\text{coth}{\left(\frac{\sqrt{{\beta\:}_{1}}\hspace{0.17em}\left(\phi\:+{\phi\:}_{0}\right)}{2}\right)}^{2}\right)}{4\left(\epsilon\text{coth}\left(\frac{\sqrt{{\beta\:}_{1}}\hspace{0.17em}\left(\phi\:+{\phi\:}_{0}\right)}{2}\right)+1\right)},$$
$$\:\phi\:={l}_{1}y+{l}_{2}z+\frac{\varGamma\:\left(\varphi\:+1\right)}{\sigma\:}\left(\omega\:{t}^{\sigma\:}\right),\xi\:={v}_{1}y+{v}_{2}z+\frac{\varGamma\:\left(\varphi\:+1\right)}{\sigma\:}\left(\tau\:{t}^{\sigma\:}\right)+\delta\:,\:\text{a}\text{n}\text{d}\:{\upomega\:}=\pm\:\sqrt{-\frac{{a}_{2}{\beta\:}_{1}{l}_{1}^{2}+2{a}_{1}{\tau\:}^{2}+2{a}_{2}{v}_{1}^{2}+4{v}_{2}}{{a}_{1}{\beta\:}_{1}}}.$$

Case 02

β1 > 0, β3 > 0, and β2 = 2 \(\sqrt{(\beta_3,\beta_3)}\)and \((\epsilon, \eta)\) = (±1,±1)

$$\:{P}_{\text{5,6}}^{\:}\left(y,z,t\right)=\left(M\pm\:N\right){e}^{i\xi\:}\:\text{a}\text{n}\text{d}\:{P}_{\text{7,8}}^{\:}\left(y,z,t\right)=\left(-M\pm\:N\right){e}^{i\xi\:},$$
(16)
$$\:\:\text{Where},\:M=\frac{\sqrt{-\frac{2\left({a}_{1}\:{\tau\:}^{2}{\beta\:}_{3}+{a}_{3}{\beta\:}_{3}{v}_{1}^{2}+2{\beta\:}_{3}{v}_{2}\right)}{{a}_{3}{\beta\:}_{1}}}\hspace{0.17em}\sqrt{\frac{{\beta\:}_{1}}{{\beta\:}_{3}}}\hspace{0.17em}\left(\frac{\epsilon\text{sinh}\left(\sqrt{{\beta\:}_{1}}\hspace{0.17em}\left(\phi\:+{\phi\:}_{0}\right)\right)}{\text{cosh}\left(\sqrt{{\beta\:}_{1}}\hspace{0.17em}\left(\phi\:+{\phi\:}_{0}\right)\right)+\eta\:}+1\right)}{4},$$
$$N=\frac{\sqrt{-\frac{2\left({a}_{1}{\tau\:}^{2}+{a}_{2}{v}_{1}^{2}+2{v}_{2}\right)}{{a}_{3}{\beta\:}_{1}}}\hspace{0.17em}\left(\frac{\epsilon\sqrt{{\beta\:}_{1}}\hspace{0.17em}\text{cosh}\left(\sqrt{{\beta\:}_{1}}\hspace{0.17em}\left(\phi\:+{\phi\:}_{0}\right)\right)}{\text{cosh}\left(\sqrt{{\beta\:}_{1}}\hspace{0.17em}\left(\phi\:+{\phi\:}_{0}\right)\right)+\eta\:}-\frac{\epsilon{\text{sinh}}^{2}\left(\sqrt{{\beta\:}_{1}}\hspace{0.17em}\left(\phi\:+{\phi\:}_{0}\right)\right)\sqrt{{\beta\:}_{1}}}{{\left(\text{cosh}\left(\sqrt{{\beta\:}_{1}}\hspace{0.17em}\left(\phi\:+{\phi\:}_{0}\right)\right)+\eta\:\right)}^{2}}\right)}{2\left(\frac{\epsilon\text{sinh}\left(\sqrt{{\beta\:}_{1}}\hspace{0.17em}\left(\phi\:+{\phi\:}_{0}\right)\right)}{\text{cosh}\left(\sqrt{{\beta\:}_{1}}\hspace{0.17em}\left(\phi\:+{\phi\:}_{0}\right)\right)+\eta\:}+1\right)},$$
$$\phi\:={l}_{1}y+{l}_{2}z+\frac{\varGamma\:\left(\varphi\:+1\right)}{\sigma\:}\left(\omega\:{t}^{\sigma\:}\right),\:\xi\:={v}_{1}y+{v}_{2}z+\frac{\varGamma\:\left(\varphi\:+1\right)}{\sigma\:}\left(\tau\:{t}^{\sigma\:}\right)+\delta\:,\:\text{a}\text{n}\text{d}\:{\upomega\:}=\pm\:\sqrt{-\frac{{a}_{2}{\beta\:}_{1}{l}_{1}^{2}+2{a}_{1}{\tau\:}^{2}+2{a}_{2}{v}_{1}^{2}+4{v}_{2}}{{a}_{1}{\beta\:}_{1}}}$$

Case 03

\({\beta\:}_{1}>0\:\text{a}\text{n}\text{d}\:\left(\mathcal{\:}\mathcal{\:}\mathcal{E},\eta\:\right)=\left(\pm\:1,\pm\:1\:\right)\)

$$\:{P}_{\text{9,10}}^{\:}\left(y,z,t\right)=\left(M\pm\:N\right)\:{e}^{i\xi\:}\:\text{a}\text{n}\text{d}\:{P}_{\text{11,12}}^{\:}\left(y,z,t\right)=\left(-M\pm\:N\right)\:{e}^{i\xi\:},$$
(17)

Where, \(\:M=\frac{\sqrt{-\frac{2\left({a}_{1}{{\uptau\:}}^{2}{{\upbeta\:}}_{3}+{a}_{2}{{\upbeta\:}}_{3}{v}_{1}^{2}+2{{\upbeta\:}}_{3}{v}_{2}\right)}{{a}_{3}{{\upbeta\:}}_{1}}}\hspace{0.17em}{{\upbeta\:}}_{1}\left(\frac{\epsilon\text{sinh}\left(\sqrt{{{\upbeta\:}}_{1}}\hspace{0.17em}\left(\phi\:+{\phi\:}_{0}\right)\right)+\rho\:}{\text{cosh}\left(\sqrt{{{\upbeta\:}}_{1}}\hspace{0.17em}\left(\phi\:+{\phi\:}_{0}\right)\right)+{\upeta\:}\sqrt{{\rho\:}^{2}+1}}+1\right)}{2{{\upbeta\:}}_{2}},\)

$$\:N=\frac{\sqrt{-\frac{2\left({a}_{1}{\tau\:}^{2}+{a}_{2}{v}_{1}^{2}+2{v}_{2}\right)}{{a}_{3}{\beta\:}_{1}}}\hspace{0.17em}\left(\frac{\epsilon\sqrt{{\beta\:}_{1}}\hspace{0.17em}\text{cosh}\left(\sqrt{{\beta\:}_{1}}\hspace{0.17em}\left(\phi\:+{\phi\:}_{0}\right)\right)}{\text{cosh}\left(\sqrt{{\beta\:}_{1}}\hspace{0.17em}\left(\phi\:+{\phi\:}_{0}\right)\right)+\eta\:\sqrt{{\rho\:}^{2}+1}}-\frac{\left(\epsilon\text{sinh}\left(\sqrt{{\beta\:}_{1}}\hspace{0.17em}\left(\phi\:+{\phi\:}_{0}\right)\right)+\rho\:\right)\sqrt{{\beta\:}_{1}}\hspace{0.17em}\text{sinh}\left(\sqrt{{\beta\:}_{1}}\hspace{0.17em}\left(\phi\:+{\phi\:}_{0}\right)\right)}{{\left(\text{cosh}\left(\sqrt{{\beta\:}_{1}}\hspace{0.17em}\left(\phi\:+{\phi\:}_{0}\right)\right)+\eta\:\sqrt{{\rho\:}^{2}+1}\right)}^{2}}\right)}{2\left(\frac{\epsilon\text{sinh}\left(\sqrt{{\beta\:}_{1}}\hspace{0.17em}\left(\phi\:+{\phi\:}_{0}\right)\right)+\rho\:}{\text{cosh}\left(\sqrt{{\beta\:}_{1}}\hspace{0.17em}\left(\phi\:+{\phi\:}_{0}\right)\right)+\eta\:\sqrt{{\rho\:}^{2}+1}}+1\right)},$$
$$\:\phi\:={l}_{1}y+{l}_{2}z+\frac{\varGamma\:\left(\varphi\:+1\right)}{\sigma\:}\left(\omega\:{t}^{\sigma\:}\right),\xi\:={v}_{1}y+{v}_{2}z+\frac{\varGamma\:\left(\varphi\:+1\right)}{\sigma\:}\left(\tau\:{t}^{\sigma\:}\right)+\delta\:,\:\text{a}\text{n}\text{d}\:{\upomega\:}=\pm\:\sqrt{-\frac{{a}_{2}{\beta\:}_{1}{l}_{1}^{2}+2{a}_{1}{\tau\:}^{2}+2{a}_{2}{v}_{1}^{2}+4{v}_{2}}{{a}_{1}{\beta\:}_{1}}}$$

Result and discussions

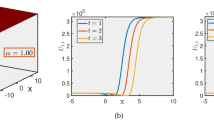
The optical soliton solution has more significance to describe the complex phenomena in nonlinear media. Here we presented some optical soliton solutions for paraxial wave model with 3D and 2D plots. This model has applications in various fields of optics and wave propagation and uses to model the evolution of slowly varying wave envelopes in nonlinear and dispersive media. In nonlinear optics, it describes the propagation of light in a medium with both linear and nonlinear refractive indices. This equation is also relevant in modeling phenomena like beam self-focusing, pattern formation, and the stability of optical beams, which are essential for applications in laser technology, optical communication systems, and materials science. For the special values of the free parameters, we presented periodic wave, diverse breather wave, and lump wave etc. the obtained solution has significance including periodic waves repeat over a regular interval and are crucial for understanding wave stability, resonance phenomena, and pattern formation in optical systems. They serve as fundamental solutions for more complex wave interactions, breathers are localized waves that oscillate in both time and space. They are essential in studying energy localization and transfer in optical fibers and nonlinear media, modeling phenomena like rogue waves. Additionally, this section also analyzes the impact of the fractional parameter \(\:\sigma\:\) on the soliton solutions obtained for the paraxial wave model using the modified extended auxiliary mapping method. Describing the complex wave of the Paraxial wave model affiliated with the different versions of soliton solutions is essential. Figures (1–5) depict the numerical solutions for the specific values of the free parameters. If we consider the value of the fractional parameter \(\:\sigma\:=0.1,\:0.5\:\)and 0.9, then the complex model reverses its original form. Figure 1 illustrates singular periodic wave of\(\:\:{|P}_{1}\left(0,z,t\right)|\:\) for suitable choice of the parametric values that \(\:\epsilon=1,\:{\beta\:}_{1}=1,\:{\beta\:}_{3}\:=2,\:{a}_{1}=0.02,\:{a}_{2}=1,\:{a}_{3}=0.01,\:\:\tau\:=0.09,\:\:{\upsilon\:}_{1}=1,\:\:{\upsilon\:}_{2}=1,\:\:{v}_{2}=1,\:\:\)\({l}_{1}=1,\:\:{\varphi\:}_{0}=1,\:\:{\varphi\:}_{\:}\:=\:1,\:\delta\:\:=\:1,\:\:\sigma\:\:=\:0.5,\:\)and y = 0. In similar marks of the above parameter, Fig. 2 represents singular periodic wave of the imaginary value of \(\:{P}_{1}\left(0,z,t\right)\) for the values \(\:\epsilon=1,\:{\beta\:}_{1}=1,\:\:{\beta\:}_{3}\:=2,\:{a}_{1}=0.02,\:\:{a}_{2}=1,\:{a}_{3}=0.01,\:\:\tau\:=0.09,\:{\upsilon\:}_{1}=1,\:{\upsilon\:}_{2}=1,\)\(\:{v}_{2}=1\:{l}_{1}=1,\:{\varphi\:}_{\:}=1\:{\varphi\:}_{0}\:=\:1,\:\delta\:\:=\:1,\:\sigma\:\:=\:0.5\) and \(\:y=0\). Figure 3 represents periodic bell shape of the imaginary portion of \(\:{P}_{1}\left(0,z,t\right)\) for the value of \(\:\epsilon=-1,\:\:{\beta\:}_{1}=1,\:{\beta\:}_{3}\:=2,\:\:{a}_{1}=0.02,\:\:{a}_{2}=1,\:{a}_{3}=0.01,\:\tau\:=0.9,\:\:{\upsilon\:}_{1}=1,\:{\upsilon\:}_{2}=1\)\(\:{v}_{2}=1,\:{l}_{1}=1,\:{\varphi\:}_{\:}=1\)\({\varphi\:}_{0}\:=\:1,\:\:\delta\:\:=\:1,\:\:\sigma\:\:=\:0.5\) and \(\:y=0\) in Fig. 4 represents a periodic wave of the absolute portion of \(\:{P}_{5}\left(0,z,t\right),\) for the values of \(\:\epsilon=-1,\:{\beta\:}_{1}=1,\:{\beta\:}_{3}\:=2,\)\({a}_{1}=0.02,\:{a}_{2}=1,\:{a}_{3}=0.01,\)\(\tau\:=0.1,\:{\upsilon\:}_{1}=1,\:\)\({\upsilon\:}_{2}=1,\:{v}_{2}=1,\)\(\:{l}_{1}=1,\:C=1,\:{\varphi\:}_{0}\:=\:1,\:\delta\:\:=\:1,\:\:\sigma\:\:=\:0.1,\:\eta\:=1\) and \(\:y=0\:\)and Fig. 5 represents a kink shape with soliton solution of absolute value of \(\:{P}_{9}\left(0,z,t\right)\) here we replace the constant value of the longitudinal for the place of transverse all other parameters value are obtained as follow \(\:p=1,\:\epsilon=-1,\:{\beta\:}_{1}=2,\:\)\({\beta\:}_{3}\:=1,\:{a}_{1}=0.1,\:\)\({a}_{2}=1,\:{a}_{3}=0.2,\:\:\tau\:=1,\:\)\({\upsilon\:}_{1}=1,\:{\upsilon\:}_{2}=1,\:{v}_{2}=1,\)\(\:{l}_{1}=1,\:C=1,\:\)\({\varphi\:}_{0}\:=\:1,\:\)\(\delta\:\:=\:1,\:\sigma\:\:=\:0.9,\:\eta\:=-1\) and \(\:y=0\). We obtained the solutions of singular periodic, periodic bell, bell shape, singular soliton etc. for the special values of the parameters. The two-dimensional wave feature also depicted for the different standard of fractional parameter \(\:\sigma\:=0.1,\:0.5\) and \(\:0.9\) with different interval of \(\:t\) that shown the potentiality of M-fractional derivative more effectively.

Fig. 1
figure 1

For the values of \(\:\:\epsilon=1,\:{\beta\:}_{1}=1,\:\)\({\beta\:}_{3}\:=2,\:{a}_{1}=0.02,\:{a}_{2}=1,\:{a}_{3}=0.01,\)  \(\tau\:=0.09,\:\:{\upsilon\:}_{1}=1,\:\:\)\(\tau\:=0.09,\:\:{\upsilon\:}_{1}=1,\:{\upsilon\:}_{2}=1,\)\({v}_{2}=1,\:\:{l}_{1}=1,\:\:{\varphi\:}_{\:}=1,\:\:{\varphi\:}_{0}\:=\:1,\:\delta\:\:=\:1,\:\:\sigma\:\:=\:0.5,\:y=0,\:\) (a) represents singular periodic wave of the \(\:\left|{P}_{1}\left(0,z,t\right)\right|\:,\) (b) represents the contour plot and (c) represents two dimensional plot for \(\:z=1\) with interval \(\:0\le\:t\le\:4\).

Full size image
Fig. 2
figure 2

For the values of \(\:\epsilon=1,\:{\beta\:}_{1}=1,\:\:{\beta\:}_{3}\:=2,\:{a}_{1}=0.02,\:\:{a}_{2}=1,\:{a}_{3}=0.01,\:\:\tau\:=0.09,\)\({\upsilon\:}_{1}=1,\:{\upsilon\:}_{2}=1,\:{v}_{2}=1\:{l}_{1}=1,\:\varphi\:=1\:{\varphi\:}_{0}\:=\:1,\:\delta\:\:=\:1,\:\sigma\:\:=\:0.5,\:\:y=0\) (a) represents singular periodic wave of the \(\:Im\left({P}_{1}\left(0,z,t\right)\right)\:,\) (b) represents the contour plot and (c) represents two dimensional plot for \(\:z=1\) with interval \(\:0\le\:t\le\:4\).

Full size image
Fig. 3
figure 3

For the values of \(\:\epsilon=-1,\:\:{\beta\:}_{1}=1,\:{\beta\:}_{3}\:=2,\:\:{a}_{1}=0.02,\:\:{a}_{2}=1,\:{a}_{3}=0.01,\:\tau\:=0.9,\)\({\upsilon\:}_{1}=1,\:{\upsilon\:}_{2}=1\:{v}_{2}=1,\:{l}_{1}=1,\:\varphi\:=1\:{\varphi\:}_{0}\:=\:1,\:\:\delta\:\:=\:1,\:\:\sigma\:\:=\:0.5,\:y=0\) (a) represents periodic bell shape of the \(\:Im\left({P}_{1}\left(0,z,t\right)\right)\:,\) (b) represents the contour plot and (c) represents two dimensional plot for \(\:z=4\) with interval \(\:0\le\:t\le\:10\).

Full size image
Fig. 4
figure 4

For the values of \(\:\epsilon=-1,\:{\beta\:}_{1}=1,\:{\beta\:}_{3}\:=2,\:{a}_{1}=0.02,\:{a}_{2}=1,\:{a}_{3}=0.01,\:\tau\:=0.1,\)\({\upsilon\:}_{1}=1,\:{\upsilon\:}_{2}=1,\:{v}_{2}=1,\:{l}_{1}=1,\:\varphi\:=1,\:{\varphi\:}_{0}\:=\:1,\:\delta\:\:=\:1,\:\:\sigma\:\:=\:0.1,\:y=0\:\eta\:=1;\) (a) represents periodic wave of the \(\:\left|\left({P}_{5}\left(0,z,t\right)\right)\right|\:,\) (b) represents the contour plot and (c) represents two dimensional plot for \(\:z=1\) with interval \(\:0\le\:t\le\:1\).

Full size image
Fig. 5
figure 5

For the values of \(\:p=1,\:\epsilon=-1,\:{\beta\:}_{1}=2,\:{\beta\:}_{3}\:=1,\:{a}_{1}=0.1,\:{a}_{2}=1,\:{a}_{3}=0.2,\)\(\tau\:=1,\:{\upsilon\:}_{1}=1,\:{\upsilon\:}_{2}=1,\:{v}_{2}=1,\:{l}_{1}=1,\varphi\:=1,\:{\varphi\:}_{0}\:=\:1,\:\delta\:\:=\:1,\:\sigma\:\:=\:0.9,\:y=0,\:\eta\:=-1;\) (a) represents periodic wave of the \(\:\left|{P}_{5}\left(0,z,t\right)\right|\:,\) (b) represents the contour plot and (c) represents two dimensional plot for \(\:z=1.55\) with interval \(\:0\le\:t\le\:2\).

Full size image

Comparisons

In this segment, we will compare the attained solutions of the M-fractional Paraxial Wave equation with unified technique by Mahtab Uddin et al59.. They explored the optical soliton solutions to the fractional form of Eq. (1) utilizing the unified method and found 24 solutions (Please see in Ref59). Similarly, we have found 12 exact solutions of Eq. (1) by utilizing the modified extended auxiliary mapping method in this article. They has been gotten various type of periodic wave, interaction of soliton solution we also obtain such type periodic wave and also obtain distinct wave solution of our proposed the M-fractional Paraxial Wave equation. We have examined the impacts of a portion of these wave profiles which can be plainly grasped by the 2D profiles. These wave ways of behaving are applied to numerous likely regions. We also compare the attained solutions of the Paraxial Wave equation with unified technique by Naeem Ullah60. He explored the solutions to the fractional form of Eq. (1) with Kerr law through the Kudryashov method and Tanh Method. He found only two solution for Kudryashov method and ten solution for Tanh method. He only discusses the ordinary drak bright and periodic solution for the Kudryashov method and Tanh Method. Anyway this original copy prompted the revelation of new, exact solitons for various kinds of waves, including intermittent, dim and splendid chime, endlessly wrinkle with soliton arrangement. Parameter values can have a significant impact on mathematical physics and nonlinear optics as well as the dynamics of optical soliton solutions in the paraxial wave model.

Conclusion

We have successfully and efficiently implemented the modified extended auxiliary mapping method to solve the M-fractional Paraxial Wave equation. Our approach has led to the discovery of new, precise solitons for different types of waves, including periodic, dark and bright bell, kink, and kink with soliton solution. By using the M-truncated fractional derivative, we have converted the fractional order of the governing equation into an integer order. This has allowed us to better understand the behavior of optical solitons, which can travel long distances without dissipating, thanks to specific nonlinear effects that offset dispersion effects. We have also created graphical representations of particular types of solitary wave solutions by assigning appropriate values to the parameters. Our chosen values for the fractional and free parameters have important implications, such as enabling the separation of the magnitudes of these parameters from a distinct function, which allows for the generation of unique, meaningful solutions. Through bifurcation, we may infer that changing the parameter values can affect the dynamics of the paraxial wave model’s optical soliton solutions and significantly impact nonlinear optics and mathematical physics. In conclusion, our technique effectively showcases the significance and importance of this entire endeavor.