Excited ion-scale turbulence by a magnetic island in fusion plasmas

Abstract

The characteristics of ion-scale turbulence in the presence of a magnetic island are numerically investigated using a gyrokinetic model in fusion plasma. We observe that in the absence of the usual ion temperature gradient (ITG) drive gradient, a magnetic island and its flatten effect could drive ITG instability. The magnetic island (MI) not only drives high-n modes of ITG instability but also induces low-n modes of vortex flow. Moreover, as the magnetic island width increases, the width of the vortex flow also increases. This implies that wider islands may more easily induce vortex flows. The study further indicates that the saturated amplitude and transport level of MI-induced ITG turbulence vary with different magnetic island widths. In general, larger magnetic islands enhance both particle and heat transport. When the magnetic island width reaches to 21ρ_i, the turbulence-driven transport becomes the same level with the cases that ITG is driven by pressure gradients. Our findings indicate the presence of intricate nonlinear effects in the modulation of plasma turbulence by MIs. These effects are of significant importance for comprehending the phenomenon of nonlinear coupling in forthcoming tokamaks such as ITER.

Introduction

Magnetic islands are ubiquitous structures generated during the magnetic field reconnection process in magnetized fusion plasmas. In this universal phenomenon, unstable current sheets release magnetic energy through the reconnection process, leading the system to transition to a lower energy state by altering its topological structure—ultimately forming a magnetic island. This process is known as the tearing mode instability¹. Due to the disruption of nested magnetic flux surfaces in the plasma, magnetic islands are considered a fundamental component of plasma transport. Currently, it is widely acknowledged that magnetic islands play a dual role in the confinement of fusion plasmas². On one hand, the presence of magnetic islands induces a change in magnetic topology, creating fast radial transport channels through the X-point (reconnection point) in the stochastic region surrounding the island separatrix. This results in a reduction in plasma confinement. The rapid growth of magnetic islands can also lead to plasma disruptions^3,4. On the other hand, magnetic islands are believed to contribute to the formation of internal transport barriers (ITBs) in the plasma. A stationary magnetic island generates strong shear flows near its separatrix, acting as a transport barrier and reducing the power threshold for ITB formation. Besides, This dual nature of magnetic islands makes their impact on turbulent transport a crucial and active area of research in plasma transport and confinement studies in fusion plasmas^5,6,7,8.

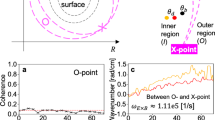
In recent years, with the development of advanced turbulence diagnostics and control methods for magnetic islands, detailed measurement results of magnetic islands and turbulence have been achieved on various devices such as DIII-D⁹, KSTAR¹⁰, HL-2A¹¹, LHD, J-TEXT¹², and TJ-II¹³. Simultaneously, a fast reciprocating Langmuir probe is utilized to study the spectral features of the dependence of geodesic acoustic modes (GAMs) and their nonlinear couplings with ambient turbulence on the magnetic island width. In EAST’s H-mode discharges, the strongly coupled m/n = 1/1 internal modes triggering NTM magnetic islands have been observed, providing experimental evidence that instabilities generate magnetic islands through mode coupling^14,15. Recent experimental studies also include investigations on the impact of magnetic islands on plasma flow and turbulence in the W7-X stellarator. The results indicate that the contribution of magnetic islands to flow is maximum at the island boundaries and approaches zero near the magnetic island O-point. These observational findings share some similarities with results observed in other devices and nonlinear particle simulations¹⁶.

Gyrokinetics¹⁷ has been extensively employed to investigate the interactions between magnetic islands and turbulence in toroidal fusion devices. Zarzoso et al. used the gyrokinetic code GKW to study the impact of rotating magnetic islands on ion temperature gradient (ITG) turbulence, revealing that in the nonlinear phase, magnetic islands can suppress turbulence levels within the island by up to 50% compared to the case without islands¹⁸. Similar results have been confirmed by local GENE simulations, showing that helical flows on both sides of the magnetic island exhibit increased shear strength⁹. In addition to early fluid studies on the impact of polarization currents on turbulent transport in small magnetic islands¹⁹, a theoretical analysis of the influence of magnetic islands on ITG stability using gyrokinetic theory in slab geometry has been conducted. In this context, the flattening effect of magnetic islands is considered²⁰. Recently, Zhang et al. investigated the influence of a magnetic island (MI) on electrostatic toroidal ITG mode. They found that when considering only the flattening effect of the magnetic island, the ITG mode can be stabilized compared to the case without the magnetic island. Moreover, their results indicate that the destabilizing effects of the MI-scale ${\varvec{E}}\times {\varvec{B}}$ flow dominate over the stabilizing effects of the flattened profile, providing theoretical evidence for the complex processes involving the influence of magnetic islands on ITG²¹.

As mentioned before, in addition to the research on the mutual influence between magnetic islands (MIs) and turbulence, another focus is on nonlinear mode coupling. Nonlinear mode coupling refers to the mutual evolution of low-n tearing modes of magnetic islands and smaller scale turbulence (higher mode numbers). This interaction has been extensively studied using fluid models²², with a few exceptions²³. It involves a two-way interaction, where not only is turbulence generated from magnetic islands, but there is also the phenomenon of turbulence nonlinearly coupling to generate magnetic islands. Regarding the latter, multiple numerical simulation studies have confirmed that small-scale interchange instabilities can transfer energy to the perturbation modes corresponding to magnetic islands through nonlinear three-wave interactions, thus exciting initial seed magnetic islands²⁴. For the former, the special topology of magnetic islands can lead to a type of mode coupling associated with the distribution of rational surfaces. Fluid simulations by Wang et al. found that when the width of a magnetic island exceeds a certain level, a new radial non-local plasma ion temperature gradient mode is excited within its region, termed the Magnetic Island Induced ITG (MITG) mode²⁵. However, Wang et al.’s work was conducted in a gyrokinetic fluid model, neglecting effects like Landau damping and the toroidal geometry of tokamaks. Importantly, whether magnetic islands alone can drive ITG turbulence remains unknown, as Wang et al.'s work still considers pressure gradients, which are the traditional driving source for ITG instability. Hence, providing an in-depth explanation of the nonlinear coupling between MIs and turbulence is crucial for advancing the understanding of multi-scale interactions in fusion plasmas, and this is the primary objective of the current study. In this paper, we present the global gyrokinetic analysis of the induction of ITG turbulence by a static magnetic island, and provide the first simulation-based evidence demonstrating the driving of ion-scale turbulence by magnetic islands.

Results and discussions

Simulation setup

The electrostatic gyrokinetic ions and drift kinetic electrons physics model described in Ref.²⁴ is used in our simulations. A static (m = 2, n = 1) magnetic island is added on the top of background magnetic field, which locates at r = 0.5a corresponding to q = 2 flux surface, and the island width can be adjusted by modifying a coefficient. The magnetic island is implemented by setting the perturbed magnetic vector potential $\delta {A}_{||I}=-\delta {A}_{||0}\times {R}_{0}{B}_{0}(2\theta -\xi )$, where R₀ and a are the major and minor radii of the tokamak, respectively. Similar to the definition of magnetic island width in reference¹⁸, the half-width w of the magnetic island can be expressed in terms of the amplitude of the parallel component of the magnetic vector potential, safety factor q, magnetic shear s = (r/q)(dq/dr), magnetic field strength B, and major radius R₀: ${w}^{2}=\frac{2q{\updelta A}_{||0}{R}_{0}}{Bs}$, which reflects the actual width of the magnetic island in the simulations.

The Cyclone base case-like equilibrium²⁶ is chosen in our simulations and the equilibrium safety factor (q) profile is shown in Fig. 1. Here we focus on the effect of m/n = 2/1 magnetic island on the nonlinear evolution of bulk plasma turbulence. On the plasma axis, the ion and electron temperature are T_e = T_i = 2.22 keV, the densities are n_e = n_i = 1.13 × 10¹³ cm⁻³, the magnetic field strength is B₀ = 2.01254 × 10⁴ G, the plasma beta is ${\beta }_{e}=8\uppi {\text{T}}_{e}/{B}_{0}^{2}$ = 0.25%, and the ion cyclotron radius is ${\rho }_{i}/{R}_{0}$ = 2.86 × 10⁻³. Furthermore, the characteristic scale lengths of particle density and temperature are defined as L_n = − (d ln n/dr)⁻¹, and L_T = − (d ln T/dr)⁻¹, respectively. In the center of magnetic island, i.e., q = 2 surface, we have $R_{0}/L_{T_{i}}$ = $R_{0}/L_{T_{e}}$ = 1.9, $R_{0}/L_{n_{i}}$ = $R_{0}/L_{n_{e}}$ = 1.9, and the drift wave instabilities from both ion and electron channels are linearly stable within these parameters.

Fig. 1

(a) The simulation grid of the magnetic equilibrium, (b) the safety factor q profile, (c) the temperature and density profile profiles utilized in this simulations. The vertical dashed line denotes the q = 2 RS.

Inducing of ion-scale turbulence by a magnetic island

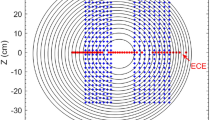
Figure 2 shows the structure of the perturbed potential component ${\updelta \upphi }^{1,2}$ and ${\updelta \upphi }^{n > 1}$ on the poloidal plane, where the width of the magnetic island (MI) is approximately 8%, 10%, 12%, 14%, 20% of the minor radius (a). Clearly, when both the magnetic island and the pressure gradient are absent, namely, the density and temperature gradients were below the threshold of unstable ITG, the mode structure is essentially at the level of very low amplitude, and identified as the trapped electron mode (TEM) mode (panel b2). In the presence of pressure gradient only, the conventional ballooning mode structure of ITG can be observed in the simulation. Interestingly, even when the density and temperature gradients fall below the threshold for instability, the ITG mode can still be driven unstable. This is because the magnetic island causes a redistribution of ion and electron particles, leading to new density and temperature profiles. These altered gradients can be of a similar magnitude to those found in the ${\eta }_{i}$ unstable ITG regime, thus driving the ITG instability. Regarding to the low-n mode structures, the electrostatic potential exhibits similar structure as the one of tearing modes, which is termed as vortex flow^23,26. Magnetic islands can resonate with the low-n modes produced during the nonlinear phase of the ITG turbulence, exciting a vortex-like electrostatic potential structure known as the vortex flow. When a magnetic island is present, the parallel motion of particles along the island’s magnetic field lines cannot be completely balanced. This imbalance triggers the formation of large-scale vortex modes coupled with the magnetic island structure. These vortex modes further facilitate the generation of ${\varvec{E}}\times {\varvec{B}}$ vortex flows around the magnetic island, effectively suppressing the turbulence levels within the island’s region.

Fig. 2

Structure of the perturbed potential component ${\updelta \upphi }^{1,2}$ and ${\updelta \upphi }^{n > 1}$ on the poloidal plane. (a1,a2) Without MI and ITG mode drive, (b1,b2) with ITG drive and without MI, (c1,c2) without ITG drive force and with MI(w/a = 8%), (d1,d2) w/a = 10%, (e1,e2) w/a = 14%, (f1,f2) w/a = 20%.

As also shown in Fig. 2, both the high-n and low-n mode structures on the poloidal plane are compared between different magnetic island widths. In general, large MI width can induce large amplitude of electrostatic potential for both low-n vortex flow and high-n ballooning mode structures. This behavior resembles the situation observed in the presence of ITG gradients as in comparison with results in Ref.²⁶. Meanwhile, the width of vortex flow increases with MI width, which implies that wider islands are favorable to drive vortex flows. This observation is consistent with the analytical results previously presented by Leconte²⁷. Starting from the extended Charney–Hasegawa–Mima equation with a non-axisymmetric equilibrium profile, M. Leconte’s analysis reveals the coupled dynamics of drift-wave (DW) turbulence and flows. The saturation level of turbulence is determined by the damping rate of the island vortex-flow. Notably, this damping rate decreases with increasing island width (w) at a rate of approximately ${1/w}^{2}$. Consequently, it predicts a nonlinear threshold ($\gamma \sim 1/{w}^{2}$) for the formation of island vortex-flows, suggesting that wider magnetic islands may facilitate flow generation. This process aligns entirely with our findings in simulations.

Furthermore, it is observed in Fig. 2 that the ITG ballooning mode structures become weak around the O-point, particularly in the case of small magnetic islands(Fig. 2c2). Additionally, the ITG mode structures exhibit not only conventional balloon-like structures, the mode structures are also observable at the inner edge of the magnetic island. This indicates that ITG structures are localized around the magnetic island, resulting in radially extended mode structures. In fact, with the exception of the results presented in Fig. 2b1 and b2, all profiles detailed in this article are derived from the descriptions in Fig. 1. The variations among these cases stem from the presence or absence of an initial magnetic island and the specified size of that island. Upon defining a magnetic island, the pressure profile evolves over the course of the simulation. Notably, the inputs for Fig. 2b1 and b2 are sourced from Fig. 1 in Ref.²⁶.

Figure 3 shows the temporal evolution of low-n and high-n modes for different magnetic island (MI) widths. It is seen that larger magnetic islands can result in higher saturation amplitudes for low-n modes. Additionally, it is noteworthy that the low-n vortex flows of magnetic island with different sizes, can exhibit nearly the same oscillation frequency, i.e., ${\omega }_{GAM}\approx 2.05{C}_{s}{/R}_{0}$, which is close to geodesic acoustic mode (GAM)²⁸, ${\omega }_{GAM}\approx \sqrt{2\left(\frac{7}{4}\right)+1}{C}_{s}/{R}_{0}=2.12{C}_{s}{/R}_{0}$, and indicates synchronous behavior between this mode and the GAM. Regarding to the characteristics of high-n mode evolution, it is seen that large magnetic island size can induce a large initial amplitude of electrostatic potential, however, the linear growth rate is less affected by the magnetic island size. In Fig. 3b, it can also be observed that, under different magnetic island widths, the final ITG amplitude is at the same order, with minimal differences. Thus, this phenomenon here is consistent with the results shown in panels (c2–f2) in Fig. 2.

Fig. 3

Time evolution of each component of ${\updelta \upphi }^{1,2}$ and ${\updelta \upphi }^{n=10,20}$.

Impact of magnetic island size on turbulent transport

Furthermore, we observed significant variations in the diffusion rate across different magnetic islands. Figure 4 illustrates the temporal evolution of the resultant effective ion diffusivity D_i(t) induced by the ITG mode across various island sizes. Here, the ion diffusivity D_i(t) are obtained by calculating near the rational surface of q = 2 as the function of time t: $D=\frac{1}{{n}_{0i}\nabla {n}_{0i}}\int d{\varvec{v}}{v}_{r}({\varvec{R}},t)\delta {f}_{i}({\varvec{R}},t)$, where $\delta {f}_{i}$ is the perturbed ion distribution function, n_0i is the equilibrium ion density, and v_r is the radial component of gyrocenter drift velocity including E × B drift and magnetic-flutter term: ${v}_{r}={v}_{E\times B}+{v}_{\delta B}$. In our computations, D_i(t) is spatially dependent quantities and is averaged over the region around the rational surface at q = 2, specifically within the range R = [1.006–1.023] m. In the case of the smallest island width (w = 8%a), the averaged ion diffusivity reaches 20 m²/s at ITG saturation but decreases to a negligible level over time. Conversely, for the larger island case (w = 20%a), the ion diffusivity remains consistently low (D_i < 1 m²/s). Generally, larger magnetic islands exhibit lower ion diffusivity near rational surfaces (q = 2), and vice versa. This phenomenon can be understood physically: as the size of the magnetic island increases, the turbulence intensity of ion density within the island is significantly suppressed, leading to almost complete disappearance of transport within the island and hence lower diffusivity levels.

Fig. 4

Time history of averaged effective ion diffusivity of ITG mode simulations with different island size.

Meanwhile, the transport characteristics of turbulence destabilized by magnetic islands are also different from turbulence transport driven by pressure gradients. Figure 5 illustrates the impact of magnetic islands on ITG turbulent transport under different magnetic island sizes. It is observed that, regardless of the magnetic island size, turbulent transport within the island is effectively suppressed. The saturation amplitude and transport level of ITG turbulence vary with different magnetic island widths. In general, larger magnetic islands are favorable to ITG destabilization in the external region of separatrix and X-point and thus enhance local particle and heat transport, which lower the plasma confinement. In comparison with the similar figure in reference²⁶, we find that when w/a = 20% (approximately 21ρ_i), the turbulence transport induced by the magnetic island can reach to a level close to the pressure gradient-driven ITG transport under similar conditions. Therefore, ITG turbulence driven by magnetic islands can have a significant impact on plasma confinement and transport. From the particle thermal conductivity depicted in Fig. 5c2–d2 and c3–d3, one can infer energy transport to a significant extent. It becomes evident that with the introduction of magnetic islands, energy primarily concentrates near the X-point or along the boundaries of the magnetic islands after a certain period. This observation implies that the flattening effect of the magnetic island induces ITG modes at its boundary, thereby facilitating energy from MI transfer to higher n mode instabilities.

Fig. 5

The impact of MI width on MI driven turbulent intensity and transport in terms of relative amplitude, particle diffusion coefficient, ion and electron thermal conductive coefficients in gyro-Bohm units. (a1–d1) w/a = 8%, (a2–d2) w/a = 14%, (a3–d3) w/a = 20%. The magnetic island structure is illustrated with the black dashed lines.

Conclusions

We conducted global nonlinear simulations using the electrostatic gyrokinetic equation, incorporating a static m/n = 2/1 magnetic perturbation, to investigate the physical processes of magnetic island (MI) driving ion temperature gradient turbulence. For the first time, our simulations indicate that in the absence of the usual ITG driving gradients, a magnetic island can still drive ITG instability. The magnetic island not only drives ITG instability in high-n modes but also induces vortex flow in low-n modes, and as the magnetic island width increases, the vortex flow width also increases. This implies that wider islands may more easily drive vortex flows.

The characteristics of ITG turbulence transport induced by magnetic islands depend on the magnetic island width. Different widths of magnetic islands result in varied saturation amplitudes and transport levels of ITG turbulence. Specifically, larger magnetic islands enhance both particle and heat transport, thereby reducing plasma confinement performance. It is worth noting that, although kinetic calculations provide more reliable results compared to fluid models, the characteristics of turbulence presented here are still driven by static magnetic islands. Future studies requiring more accurate calculations should involve self-consistent dynamic magnetic islands. Besides, in the next phase, we will also systematically analyze the complex energy exchange between magnetic islands and turbulence.

Methods

Physical model

We delve into the nonlinear repercussions of static magnetic islands on turbulent modes, employing an approach akin to that outlined in reference²⁶. Our simulation model, rooted in the gyrokinetic equation, forms the backbone of this study’s investigation:

$$\frac{d}{dt}{f}_{s}\left({\varvec{R}}, {v}_{||},\mu , t\right)=\left(\frac{\partial }{\partial t}+\dot{{\varvec{R}}}\cdot \nabla +\dot{{v}_{||}}\frac{\partial }{\partial {v}_{||}}-{C}_{coll}\right){f}_{s}=0.$$

(1)

the distribution function (${\text{f}}_{\mathrm{s}}\left(\text{R}, {\text{v}}_{||},\upmu ,\text{t}\right)$) for each particle species s is delineated across five-dimensional space, encompassing gyrocenter position ${\varvec{R}}$, parallel velocity ${v}_{||}$, and magnetic moment $\mu$. Here, ${C}_{s}$ stands for the collision operator. Importantly, collisions are omitted in the simulations. Within the framework of gyrokinetic theory, $\dot{{\varvec{R}}}$ and $\dot{{v}_{||}}$ can be succinctly described as:

$$\dot{{\varvec{R}}}={v}_{||}\frac{{\varvec{B}}}{{B}_{||}^{*}}+{{\varvec{v}}}_{{\varvec{E}}}+{{\varvec{v}}}_{{\varvec{c}}}+{{\varvec{v}}}_{{\varvec{g}}},$$

(2)

$${\dot{v}}_{||}=-\frac{1}{{m}_{s}}\frac{{{\varvec{B}}}^{\mathbf{*}}}{{B}_{||}^{*}}\cdot \left(\mu \nabla B+{Z}_{s}\nabla \delta \phi \right),$$

(3)

Here, ${Z}_{s}, {m}_{s}, c, {\varvec{B}}, \delta \phi$ denote the electric charge, particle mass, speed of light, background magnetic field, and perturbed electrostatic potential, respectively. The symbol ${\varvec{b}}\equiv \frac{{\varvec{B}}}{B}$ denotes the unit magnetic vector. The term ${\text{B}}_{||}^{*}={\text{B}}^{*}\cdot \text{b}$ corresponds to the Jacobian determinant in phase space with ${\text{B}}^{*}=\text{B}+\frac{{\text{m}}_{\text{s}}\text{c}}{{\text{Z}}_{\text{s}}}{\text{v}}_{||}\nabla \times \text{b}$. The gyrocenter velocity comprises the parallel velocity ${\text{v}}_{||}\frac{\text{B}}{{\text{B}}_{||}^{*}}$, drift velocity ${\text{v}}_{\text{E}}=\frac{\text{cb}\times \nabla {\updelta \upphi }}{{\text{B}}_{||}^{*}}$, magnetic curvature drift velocity ${\text{v}}_{\text{c}}=\frac{{\text{m}}_{\text{s}}\text{c}}{{\text{Z}}_{\text{s}}{\text{B}}_{||}^{*}}{\text{v}}_{||}^{2}\nabla \times \text{b}$, and magnetic gradient drift velocity ${\text{v}}_{\text{g}}=\frac{\text{c}\upmu }{{\text{Z}}_{\text{s}}{\text{B}}_{||}^{*}}\text{b}\times \nabla \text{B}$.

In the GTC code^28,29, the representation of magnetic islands involves introducing an additional perturbation to the background magnetic field, denoted as ${\varvec{B}}={{\varvec{B}}}_{\boldsymbol{0}}+\delta {{\varvec{B}}}_{{\varvec{I}}}$. The magnitude of this secondary term is notably smaller than that of the primary term. Upon incorporating the static island perturbation, the expressions for $\dot{{\varvec{R}}}$ and $\dot{{v}_{||}}$ can be approximated as follows:

$$\dot{{\varvec{R}}}={v}_{||}\frac{{{\varvec{B}}}_{\boldsymbol{0}}+{\varvec{\delta}}{{\varvec{B}}}_{{\varvec{I}}}}{{B}_{||}^{\mathbf{*}}}+\frac{c\left({{\varvec{b}}}_{\boldsymbol{0}}+\frac{{\varvec{\delta}}{{\varvec{B}}}_{{\varvec{I}}}}{{B}_{0}}\right)\times \nabla \delta \phi }{{B}_{||}^{*}} +\frac{{m}_{s}c}{{Z}_{s}{B}_{||}^{*}}{v}_{||}^{2}\nabla \times {{\varvec{b}}}_{\boldsymbol{0}}+\frac{c\mu }{{Z}_{s}{B}_{||}^{*}}{{\varvec{b}}}_{\boldsymbol{0}}\times \nabla {B}_{0},$$

(4)

$$\dot{{v}_{||}}=-\frac{1}{{m}_{s}}\frac{{{\varvec{B}}}_{\boldsymbol{0}}^{\mathbf{*}}+{\varvec{\delta}}{{\varvec{B}}}_{{\varvec{I}}}}{{B}_{||}^{*}}\cdot \left(\mu \nabla {B}_{0}+{Z}_{s}\nabla \delta \phi \right)-c{v}_{||}\frac{\nabla \times \left(\frac{{\varvec{\delta}}{{\varvec{B}}}_{{\varvec{I}}}}{{B}_{0}}\right)}{{B}_{||}^{*}}\cdot \nabla \delta \phi .$$

(5)

Following the $\delta f$ methodology, the propagator $d/dt\equiv L$ and the distribution function ${f}_{s}$ must be decomposed into an equilibrium component devoid of magnetic islands and a perturbed component. Initially setting the propagator as $L={L}_{0}+\delta L$, we obtain:

$${L}_{0}=\frac{\partial }{\partial t}-\frac{\mu }{{m}_{s}}\frac{{{\varvec{B}}}_{\boldsymbol{0}}^{\mathbf{*}}}{{B}_{0||}^{*}}\cdot \mu \nabla {B}_{0}\frac{\partial }{{\partial }_{{v}_{||}}}+{v}_{||}\frac{{{\varvec{B}}}_{\boldsymbol{0}}}{{B}_{0||}^{*}}\cdot \nabla +\left(\frac{{m}_{s}c}{{Z}_{s}{B}_{||}^{*}}{v}_{0||}^{2}\nabla \times {{\varvec{b}}}_{\boldsymbol{0}}+\frac{c\mu }{{Z}_{s}{B}_{0||}^{*}}{{\varvec{b}}}_{0}\times \nabla {B}_{0}\right)\cdot \nabla ,$$

(6)

$$\begin{aligned}\delta L&=\left(\frac{{B}_{0||}^{*}}{{B}_{||}^{*}}-1\right){L}_{0}+\left({v}_{||}\frac{{\varvec{\delta}}{{\varvec{B}}}_{{\varvec{I}}}}{{B}_{||}^{*}}+\frac{c\left({{\varvec{b}}}_{\boldsymbol{0}}+\frac{{\varvec{\delta}}{{\varvec{B}}}_{{\varvec{I}}}}{{B}_{0}}\right)\times \nabla \delta \phi }{{B}_{||}^{*}}\right)\cdot \nabla \\ &\quad -\frac{1}{{m}_{s}}\frac{{{\varvec{B}}}_{\boldsymbol{0}}+{\varvec{\delta}}{{\varvec{B}}}_{{\varvec{I}}}}{{B}_{||}^{*}}\cdot {Z}_{s}\nabla \delta \phi \frac{\partial }{{\partial }_{{v}_{||}}}-\frac{1}{{m}_{s}}\frac{{\varvec{\delta}}{{\varvec{B}}}_{{\varvec{I}}}}{{B}_{||}^{*}}\cdot \mu \nabla {B}_{0}\frac{\partial }{{\partial }_{{v}_{||}}}\\ &\quad -c{v}_{||}\frac{\nabla \times \left({{\varvec{b}}}_{\boldsymbol{0}}+\frac{{\varvec{\delta}}{{\varvec{B}}}_{{\varvec{I}}}}{{B}_{0}}\right)}{{B}_{||}^{*}}\cdot \nabla \delta \phi \frac{\partial }{{\partial }_{{v}_{||}}}.\end{aligned}$$

(7)

Likewise, we decompose the distribution function ${f}_{s}={f}_{0s}+\delta {f}_{s}$, where ${f}_{0s}$​ represents the equilibrium portion, which remains time-independent and satisfies the condition ${L}_{0}{f}_{0s}=0$. By defining the particle weight as ${w}_{s}=\delta {f}_{s}/{f}_{s}$ and considering that ${L}_{0}{f}_{0s}=0$ and $\left({L}_{0}+\delta L\right)\left({f}_{0s}+\delta {f}_{s}\right)=0$, we derive the evolution equation for ${w}_{s}$:

$$\frac{d}{dt}{w}_{s}=-\frac{1}{{f}_{s}}\delta L{f}_{0s}= -\left(1-{w}_{s}\right)\times \left[\begin{array}{l} {\underbrace {{\frac{{c\left( {\varvec{B}_{\boldsymbol{0}} + {\boldsymbol{\delta}} {\varvec{B}}_{{\varvec{IS}}} } \right) \times \nabla \delta \phi }}{{B_{0}^{2} }} \cdot \frac{1}{{f_{{0s}} }}\left. \nabla \right|_{{v \bot }} f_{{0s}} }}_{{E \times B}}} \\ + {\underbrace {{ \frac{{v_{{||}} Z_{s} }}{{T_{{0s}} }}\left( {\frac{{\varvec{B}_{\boldsymbol{0}} + \varvec{\delta B}_{{\varvec{IS}}} }}{{B_{0} }} \cdot \nabla \delta \phi } \right)}}_{{parallel}}} \\ +{\underbrace {{ \frac{{Z_{s} }}{{T_{{0s}} }}\left( {\frac{{v_{{||}}^{2} }}{{{{\Omega }}_{s} }}\nabla \times \varvec{b}_{\boldsymbol{0}} + \frac{\mu }{{m_{s} {{\Omega }}_{s} }}\varvec{b}_{\boldsymbol{0}} \times \nabla \varvec{B}_{\boldsymbol{0}} } \right) \cdot \nabla \delta \phi }}_{{magnetic\; drift}}} \\ + {\underbrace {{v_{{||}} \frac{{\varvec{\delta B}_{{\varvec{IS}}} }}{{B_{0} }} \cdot \frac{1}{{f_{{0s}} }}\nabla \left. \right|_{{v_{ \bot } }} f_{{0s}} }}_{{flatten\;effect}}} \end{array}\right].$$

(8)

Here, ${\Omega }_{s}={Z}_{s}{B}_{0}/{m}_{s}c$ represents the particle cyclotron frequency with the gradient operator $\nabla {|}_{{v}_{\perp }}{f}_{0s}=\left(\nabla +\frac{\mu \nabla {B}_{0}}{{T}_{0s}}\right){f}_{0s}.$ Since the effects of magnetic islands on drift terms are neglected, we set ${B}_{0||}^{*}={B}_{||}^{*}={B}_{0}.$ Once $\delta {f}_{s}$ is obtained, the perturbation density, current, and pressure can be determined. Additionally, the gyrokinetic Poisson equation is required and is expressed as follows:

$$\frac{{Z}_{i}^{2}{n}_{0i}}{{T}_{0i}}\left(\delta \phi -\delta \widetilde{\phi }\right)={Z}_{i}\delta {n}_{i}+{Z}_{e}\delta {n}_{e}.$$

(9)

Here $\delta \widetilde{\phi }\left({\varvec{x}},t\right)=\frac{1}{{n}_{i}}{\int }_{{\varvec{R}}\to {\varvec{x}}}d{\varvec{v}}{f}_{i}\left({\varvec{R}},\mu ,{v}_{||},t\right)\delta \overline{\phi }({\varvec{R}},t)$ represents the result of transforming the cyclotron-averaged potential $\delta \overline{\phi }({\varvec{R}},t)$ back to the real coordinates. Equations (1–10) constitute a self-contained system that can be employed to simulate the ion temperature gradient (ITG) instability in plasmas featuring magnetic islands.

Simulation approach

In our previous work, the focus was on the influence of magnetic islands on pressure-driven (${\eta }_{i}$) ITG turbulence. For comparison, this study addresses the impact of magnetic islands on the destabilization of ITG instability and turbulence. In the physical perspective, electrons are characterized by large thermal velocity and can rapidly respond to low-frequency perturbations, such as the electric field of ITG instability. Therefore, the primary response of electrons is adiabatic, with the adiabatic response predominantly involving the non-zonal flow component of the perturbed electric field on magnetic surfaces. However, distinguishing this zonal flow component with a concerning magnetic island topology is computational challenging. For example, many existing large-scale numerical simulation codes struggle to calculate the electron adiabatic response relevant to magnetic island topology. To overcome this challenge, we directly employ the drift kinetic model for electrons without orbit averaging, which allows to evolve the complete electron distribution function including the adiabatic component. Moreover, the drift kinetic treatment on electrons has the additional benefit that can incorporate the comprehensive electron dynamics in the presence of magnetic islands, which can be important to electron-driven modes^28,30.

In addition, we define the ion and electron thermal conductivity ${\chi }_{i}$ and ${\chi }_{e}$ as:

$${\chi }_{x}=\frac{1}{{n}_{0x}\nabla {T}_{0x}}\int d{\varvec{v}}\left(\frac{1}{2}{m}_{x}{v}^{2}-\frac{3}{2}{T}_{x}\right){v}_{r}\delta {f}_{x}$$

(10)

The transport coefficients are normalized by the gyro-Bohm unit which is defined as ${D}^{GB}={\chi }_{i}^{GB}={\rho }_{i}^{2}{v}_{i}/a$.