Introduction

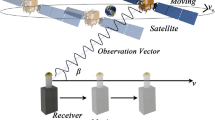
Radar is a crucial space TT&C equipment, as depicted in Fig. 1. It employs electromagnetic waves to detect and locate targets1. The fundamental principle involves emitting electromagnetic waves to illuminate the target and to receive the reflected echoes, from which information such as range, direction, and elevation can be determined2.

Fig. 1
figure 1

Radar Equipment Schematic Diagram (Photo from Chinanews.com).

Full size image

Before employing radar to track and measure spacecraft states, the radar system is usually calibrated to improve the accuracy3. The primary objective of zero value calibration is to precisely determine the zero biases of the radar angle and range sensors, isolate system errors and evaluate accuracy, and apply corrections to real-time observation data, resulting in high-precision spacecraft orbit and trajectory parameters4. Among these tasks, determining the radar center point and its coordinates is the initial and critical step, directly impacting the subsequent measurement reliability.

Theoretically, the radar rotation center is conventionally defined as the intersection of the vertical and horizontal axes, serving as the reference point for all measurements5. This point exists physically inside the radar base, presenting significant challenges in determining its coordinates due to practical limitations. Observers cannot access the interior for direct position determination, and the point is invisible and intangible, precluding the placement of any physical markers like survey prisms. Satellite positioning signals are also obstructed6. Consequently, the current primary method is to set up multiple observation stations around the radar and employ Total Station Trilateration (TST) technique to determine the radar rotation center position (refer to Chap. 2). This traditional approach is outdated, time-consuming, costly, and yield low efficiency and return on investment7.

In some literature, scholars have deeply studied TST and its application, and some papers deal with GNSS high-precision measurements, both are worthy of our learning and consideration for radar rotation center determination. Zhao Liang (2024) proposed a method of using GNSS rapid static measurement to detect the stability of control points based on the need for control network retesting in engineering projects8. This method shortens field measurement time, reduces manpower and material resources, lowers work intensity, and improves work efficiency compared to ordinary static measurement. However, this method also has its limitations, as it does not form a synchronous observation loop and cannot form a closed shape, resulting in slightly lower reliability. To determine the inaccessible phase center point coordinates of large parabolic antennas, Fan Cheng Xiao etc. (2023) proposed a three-axis center positioning method based on a total station9. By combining polar coordinate method with directional intersection technique, the phase center coordinates can be accurately obtained. They concluded that their method has good applicability for the three-axis center measurement of most large antennas. However, when the observation instruments and environment are severely limited, it may be necessary to increase a considerable number of points to participate in the calculation which may reduce efficiency. Roman Shults etc. (2022) used quantitative techniques to simulate and analyze the displacements of gas pipeline overpasses, which were measured in two epochs by using terrestrial laser scanning and the total station10. The measurement results met expectations. But the result is restricted to the specific discrete points measured by the total station. D.N. Dong etc. (2022) introduced the conceptual design and derivable products of multi-antenna synchronized GNSS receivers for attitude determination, multi-path effect mitigation, phase center variation correction, and ground-based carrier phase windup calibration11. Through case studies, the relative and absolute PCV can be measured directly, which can reduce the rank defect of the observation equation and improve the accuracy of measurement results. But this method is feasible only when the distance between the two antennas is short. Thus, solutions of wider applicability need to be further studied. Jun Wu etc. (2016) discovered the main limitations of existing total station technology, such as poor efficiency and single tasking, and proposed a novel total station measurement method by using multi-laser plane constraints established through rotating planar planes and distance information obtained with an ultrasonic ranging method12. The positioning method can achieve accurate, multi-tasking, real-time, and circumferential measurement. However, further exploration is needed regarding the calibration methods of total stations and the potential industrial applications of the proposed methods. I.V. Ditskiy (2015) proposed a new method and algorithm capable of finding reliable solutions to eliminating the cyclic phase slips (ECPS)13. It can solve the problem of ECPS at long ranges from the base and gave the results of its verification using the really measured GNSS data. It is demonstrated that the developed algorithms allow obtaining a reliable fixed solution to the problem of eliminating cyclic phase slips upon the intervals of not less than one hour, and performing determination of the coordinates at a millimeter-level of precision. it is expected to modify the algorithms for processing the data of GNSS observations for the kinematic mode of positioning during the follow-on researches. It is also expected that the developed algorithms are to be used at creation of the Precise Point Positioning (PPP). E. Osada et al. (2015) proposed a method of Total Station/GNSS/EGM integrated geocentric positioning14 that was used for building precise 3D models of terrestrial objects in the GRS80 geocentric coordinate system. Mohammad O. et al. (2018) proposed a novel automatic and accurate passive target centroid detection approach applied in engineering geodesy for automatic target pointing with sub-millimeter accuracy15. Anja P. et al. (2023) presented a trajectory generation and control scheme for point-to-point motion of a hydraulically driven large-scale manipulator considering various constraints, by which position and orientation of the tool center point were generated by a constrained quadratic optimization problem, achieved positioning accuracy is in the sub-centimeter range16. V. Gikas et al. (2013) introduced the rail track surveying system which employed GPS and a tracking total station for absolute referencing, and extended test runs were conducted to validate the feasibility of the system and the method17. P. Bauer et al. (2023) discussed augmentation strategies for the automatic operation of total stations18. S. Saadati et al. (2019) constructed a horizontal Geodetic field Calibration Network19, in which they used total stations and GPS/GNSS receivers, achieving sub-millimeter precision for horizontal positions. A. A. Zadeh et al. (2022) reviewed LEO POD methods based on undifferenced GNSS observations in both post-mission and real-time data processing and discussed the most recent developments and important achievements20. C.Ogaja, et al. (2022) presented an algorithm for flagging cycle slips during data preprocessing, whose results of the study supported the National Oceanic and Atmospheric Administration’s (NOAA) GNSS services and tools for the public21. T. Suzuki (2023) evaluated the reception characteristics of the L6 signal of a compact and lightweight L6-compatible antenna and the multipath characteristics of the antenna as well, in which he provided guidelines for antenna selection when high-precision positioning using L6 signals is employed in various applications22. Rüdiger Lehmann et al. (2024) studied estimating transformation parameters from given coordinates of control points by least-squares adjustment, they focused on the internal reliability of the underlying adjustment model, established the minimum detectable bias (MDB), derived explicit formulas23.

This paper presents a new method for determining the rotation center coordinates of radar equipment using GNSS. It begins with reviewing conventional technique and discussing its limitations. Then the paper delves into the principles, mathematical model, and data processing algorithm of the GNSS-based approach. A corresponding software-hardware system has been developed accordingly. Next, an experimental validation scheme is designed and carried out at a TT&C monitoring station, where both the GNSS based method and traditional approach were utilized and the observation data was processed to substantiate the superiority of the new method.

In the following Chapters, when we talk about the coordinates, the local level system is chosen, which is transformed from WGS84 coordinate system.

Traditional approaches

At present the conventional method for determining the rotation center of radar equipment primarily uses total station technology that needs setting up multiple control points around the radar. First, several control points are set up, and their coordinates in local level frame are measured by static GNSS positioning. Then, the total station is placed on control point, with its telescope aims at the edges of the radar antenna, illustrated in Fig. 2 as the blue and green dashed lines representing the line of sight. The two solid lines represent the angle bisectors between dashed lines projected vertically onto the upper surface of radar pitch-box, and their intersection point (called as quasi-center in Fig. 2) is on the radar’s vertical axis. Then the distance and angle to the quasi-center are measured, from which the local level coordinate of measured quasi-center can be derived by combining distance, angle and local level coordinates of the control points. The rotation center is located just under the quasi-center, about half-height of the pitch-box, along with the vertical axis. Consequently, the horizontal position of rotation center can be considered as the same with quasi-center, its height is about half-height of the pitch-box lower than that of quasi-center.

In practice, this TST method involves repeatedly setting up the total station at several control points, conducting multiple forward-intersection observations, and spending a lot of time to intersect the quasi-center for redundancy on the pitch-box surface24.

Fig. 2
figure 2

Schematic diagram of traditional total station intersection method.

Full size image
Fig. 3
figure 3

Manual marking the intersection point for TST technique (Photo by research team).

Full size image

To manually mark the intersection point, at least 2 persons are required to climb and operate on the pitch-box, as depicted in Fig. 3. The process requires not only complex observation, resulting in time-consuming, labor-intensive, low efficiency and high cost. Moreover, since that radar antenna is usually tens of meters high, with smooth surfaces and limited maneuverability, the operation process is dangerous for surveyors. Additionally, this method is technically backward and easy to cause systematic error25. What is important, that the measured point is a quasi-center that is not the rotation center we want, needs to be transformed that would cause errors in practice.

The proposed new method

The new method presented in this article is based on the high-precision carrier phase static relative GNSS positioning method. Due to the rotation center point being inside the radar pitch-box and existing only as a spatial geometric concept with no tangible physical target, as illustrated in Fig. 3, it is impossible to place a GNSS antenna at the exact real center of the radar equipment. Even if an attempt were made to align the antenna phase center with the radar center, the GNSS antenna would still not be able to receive satellite signal.

This paper proposes an analytic geometry method in 3D space based on GNSS satellite positioning. The innovation idea is that inaccessible point position determination problem is converted to a simple determining intersection of planes and lines, for which the high precision GNSS satellite measurements were here used to calculate the plane-equation, intersection lines-equation and then the intersection point position as the radar center.

We specifically designed and developed a multi-constellation dual frequency GNSS receiver device with antenna to track navigation satellites. In measurement practice, to improve accuracy, two GNSS antennas (hereafter as the primary and auxiliary antenna) are used.

As illustrated in Fig. 4, the two GNSS antennas were fixed symmetrically on the opposite edge of the radar antenna. For relative GNSS positioning, a reference receiver is needed and placed on a known position point to formulate the double difference baseline solution. GNSS antennas simultaneously track the common GNSS satellites, and the collected raw data are sent to a notebook computer for radar rotation center coordinate determination by using self-developed software, illustrated in Fig. 5.

Fig. 4
figure 4

System architecture diagram.

Full size image

Reference station antenna, together with primary and auxiliary GNSS antennas respectively, can form two baselines. Double difference baseline solutions by high precision GNSS positioning can be performed, with which the radar rotation center could be determined, whose procedure will be given in details.

The operation steps and data flowchart for implementing the process are shown in Fig. 5:

Fig. 5
figure 5

Operation steps and data flowchart.

Full size image

Theoretically, using our proprietary technique, mathematical models and algorithms, it enables the automated determination of the radar center coordinate with high precision, allowing a single person to complete all measurements. The use of GNSS instead of total station, automatic surveying instead of manual observing, this innovation realizes a low-risk, low-cost and time-efficient method for determining the radar rotation center.

In practice, the several measures should be employed to avoid GNSS signal blocked and suppress the multipath effect of the radar antenna. Usually, open sky condition is satisfied around the radar. The position and height of the GNSS antennas should be carefully chosen while installing them. Before the formal observation, GNSS data over 24 h can be collected to analyze the multipath error that of each frequency is expected to be less than 0.5 m. Thus suitable satellite cut-off angle (e.g. 15°for our test) during formal data collection could be set, to deny, to the greatest extent, the reflected signal from entering the GNSS antenna.

Methodology for vertical axis determination

Methodology

First, leveling approximately and rotating horizontally the radar antenna pointing azimuth of 0°, then GNSS primary & reference antennas simultaneously track common satellites and collect the GNSS data. Secondly, with the radar antenna rotating horizontally to azimuth of 90°,180°,respectively, two above GNSS antennas continually collect observation data. Three GNSS positioning datasets can be used to determine two middle perpendicular planes(a plane which passes through the middle point of a line segment and perpendicular to the line segment), one of which (as yellow plane in Fig. 6) is formed using the positioning results of the GNSS antenna position when the radar antenna rotating horizontally to azimuth of 90°,180°, another one(as blue plane in Fig. 6) formed with the radar antenna at azimuth of 0°,90°. The intersection line of these two middle perpendicular planes defines the vertical axis (indicated by the red dashed line).

Fig. 6
figure 6

Schematic diagram of vertical axis determination method.

Full size image

In theory, the vertical axis spatial equation determination accuracy is primarily determined by the GNSS horizontal positioning precision. To ensure that GNSS positioning results meet the required accuracy, each GNSS observation time must be at least 2 h. Additionally, to maximize the accuracy of the geometric intersection line between the two middle perpendicular planes, the radar antenna rotates horizontally at azimuth of 0°, 90°, and 180°, respectively, at which GNSS antennas collect observation data.

Mathematical model and algorithm for vertical axis determination

As previously mentioned, two GNSS antennas yield two sets of raw GNSS measurement data. Taking a single GNSS antenna into account, there will get three sets of GNSS data from three observation periods corresponding to radar’s azimuth of 0°, 90°, and 180°. Then spatial geometry principles are employed to derive the equations for the two perpendicular planes. The intersection line’s equation, known as the vertical axis equation, is found out by solving these two plane equations simultaneously. For brevity, we omit the derivation steps and present the mathematical formula directly:

Assuming: the spatial rectangular coordinates (by GNSS high-precision positioning results) of the three positions of that GNSS antenna are:

$$\:\left({x}_{0},\:{y}_{0},{z}_{0}\right),\:\left({x}_{90},{y}_{90},{z}_{90}\right),\left({x}_{180},{y}_{180},{z}_{180}\right)$$

The coordinates of the midpoint of the line segment between two points are:

$$\:{x}_{o1}=\frac{{x}_{0}+{x}_{90}}{2},{y}_{o1}=\frac{{y}_{0}+{y}_{90}}{2},{z}_{o1}=\frac{{z}_{0}+{z}_{90}}{2}$$
$$\:{x}_{o2}=\frac{{x}_{90}+{x}_{180}}{2},{y}_{o2}=\frac{{y}_{90}+{y}_{180}}{2},{z}_{o2}=\frac{{z}_{90}+{z}_{180}}{2}$$

In the following, subscripts 1 and 2 are used to represent two middle perpendicular planes, respectively. The middle perpendicular plane is perpendicular to the space vector formed by the two-point connection, which is the normal vector of the middle perpendicular plane, and is written as:

Normal vector to middle perpendicular plane 1 is:

$$\:{\overset{\rightharpoonup}{n}}_{1}=\left[\begin{array}{c}\frac{{x}_{90}-{x}_{0}}{\sqrt{{({x}_{90}-{x}_{0})}^{2}+{({y}_{90}-{y}_{0})}^{2}+{({z}_{90}-{z}_{0})}^{2}}}\\\:\frac{{y}_{90}-{y}_{0}}{\sqrt{{({x}_{90}-{x}_{0})}^{2}+{({y}_{90}-{y}_{0})}^{2}+{({z}_{90}-{z}_{0})}^{2}}}\\\:\frac{{z}_{90}-{z}_{0}}{\sqrt{{({x}_{90}-{x}_{0})}^{2}+{({y}_{90}-{y}_{0})}^{2}+{({z}_{90}-{z}_{0})}^{2}}}\end{array}\right]\triangleq\:\left[\begin{array}{c}{A}_{1}\\\:{B}_{1}\\\:{C}_{1}\end{array}\right]$$
(1)

where:

$$\:\frac{{x}_{90}-{x}_{0}}{\sqrt{{({x}_{90}-{x}_{0})}^{2}+{({y}_{90}-{y}_{0})}^{2}+{({z}_{90}-{z}_{0})}^{2}}}\triangleq\:{A}_{1}$$
$$\:\frac{{y}_{90}-{y}_{0}}{\sqrt{{({x}_{90}-{x}_{0})}^{2}+{({y}_{90}-{y}_{0})}^{2}+{({z}_{90}-{z}_{0})}^{2}}}\triangleq\:{B}_{1}$$
$$\:\frac{{z}_{90}-{z}_{0}}{\sqrt{{({x}_{90}-{x}_{0})}^{2}+{({y}_{90}-{y}_{0})}^{2}+{({z}_{90}-{z}_{0})}^{2}}}\triangleq\:{C}_{1}$$

Similarly, the normal vector to middle perpendicular plane 2 can be derived as.

$$\:{\overset{\rightharpoonup}{n}}_{2}=\left[\begin{array}{c}\frac{{x}_{180}-{x}_{90}}{\sqrt{{({x}_{180}-{x}_{90})}^{2}+{({y}_{180}-{y}_{90})}^{2}+{({z}_{180}-{z}_{90})}^{2}}}\\\:\frac{{y}_{180}-{y}_{90}}{\sqrt{{({x}_{180}-{x}_{90})}^{2}+{({y}_{180}-{y}_{90})}^{2}+{({z}_{180}-{z}_{90})}^{2}}}\\\:\frac{{z}_{180}-{z}_{90}}{\sqrt{{({x}_{180}-{x}_{90})}^{2}+{({y}_{180}-{y}_{90})}^{2}+{({z}_{180}-{z}_{90})}^{2}}}\end{array}\right]\triangleq\:\left[\begin{array}{c}{A}_{2}\\\:{B}_{2}\\\:{C}_{2}\end{array}\right]$$
(2)

were

$$\:\frac{{x}_{180}-{x}_{90}}{\sqrt{{({x}_{180}-{x}_{90})}^{2}+{({y}_{180}-{y}_{90})}^{2}+{({z}_{180}-{z}_{90})}^{2}}}\triangleq\:{A}_{2}$$
$$\:\frac{{y}_{180}-{y}_{90}}{\sqrt{{({x}_{180}-{x}_{90})}^{2}+{({y}_{180}-{y}_{90})}^{2}+{({z}_{180}-{z}_{90})}^{2}}}\triangleq\:{B}_{2}$$
$$\:\frac{{z}_{180}-{z}_{90}}{\sqrt{{({x}_{180}-{x}_{90})}^{2}+{({y}_{180}-{y}_{90})}^{2}+{({z}_{180}-{z}_{90})}^{2}}}\triangleq\:{C}_{2}$$

Using the point-normal equation, we obtain the equation for the middle perpendicular plane 1 as follows:

$$\:{A}_{1}x+{B}_{1}y+{C}_{1}z=-{D}_{1}$$
(3)

where:

$$\:-{D}_{1}\triangleq\:{A}_{1}{x}_{o1}+{{B}_{1}y}_{o1}+{{C}_{1}z}_{o1}$$

\(\:({x}_{o1},{y}_{o1},{z}_{o1})\) is the GNSS positioning coordinates of the midpoint of the line segment 1.

Similarly, the spatial equation of the middle perpendicular plane 2 is:

$$\:{A}_{2}x+{B}_{2}y+{C}_{2}z=-{D}_{2}$$
(4)

where:

$$\:-{D}_{2}\triangleq\:{A}_{2}{x}_{o2}+{{B}_{2}y}_{o2}+{{C}_{2}z}_{o2}$$

\(\:({x}_{\text{o}2},{y}_{\text{o}2},{z}_{\text{o}2})\) is the GNSS positioning coordinates of the midpoint of the line segment 2.

By combing and solving Eqs. (3) and (4), we can obtain their spatial intersection line, that is:

$$\:\left\{\begin{array}{c}{A}_{1}x+{B}_{1}y+{C}_{1}z=-{D}_{1}\\\:{A}_{2}x+{B}_{2}y+{C}_{2}z=-{D}_{2}\end{array}\right.$$
(5)

In the formula:

$$\:-{D}_{1}\triangleq\:{A}_{1}{x}_{o1}+{{B}_{1}y}_{o1}+{{C}_{1}z}_{o1}$$
$$\:-{D}_{2}\triangleq\:{A}_{2}{x}_{o2}+{{B}_{2}y}_{o2}+{{C}_{2}z}_{o2}$$

The vertical axis of the radar equipment is presented by this spatial line.

In practical measurement schemes, primary and auxiliary GNSS antennas are employed for positioning, thus resulting in two vertical axis solutions. If the primary and auxiliary antennas are represented by superscripts A and B, respectively, Eq. (5) can be rewritten as:

$$\:\left\{\begin{array}{c}{A}_{1}^{A}x+{B}_{1}^{A}y+{C}_{1}^{A}z=-{D}_{1}^{A}\\\:{A}_{2}^{A}x+{B}_{2}^{A}y+{C}_{2}^{A}z=-{D}_{2}^{A}\end{array}\right.$$
(6)

where:

\(\:\left[\begin{array}{c}{A}_{1}^{A}\\\:{B}_{1}^{A}\\\:{C}_{1}^{A}\end{array}\right]\triangleq\:{\overset{\rightharpoonup}{n}}_{1}^{A}\), the unit vector of normal line of the middle perpendicular plane 1;

\(\:\left[\begin{array}{c}{A}_{2}^{A}\\\:{B}_{2}^{A}\\\:{C}_{2}^{A}\end{array}\right]\triangleq\:{\overset{\rightharpoonup}{n}}_{2}^{A}\), the unit vector of normal line of the middle perpendicular plane 2;

Equation (6) represents a vertical axis solution from the primary GNSS antenna, and similarly, Eq. (7) shows a solution from the auxiliary GNSS antenna:

$$\:\left\{\begin{array}{c}{A}_{1}^{B}x+{B}_{1}^{B}y+{C}_{1}^{B}z=-{D}_{1}^{B}\\\:{A}_{2}^{B}x+{B}_{2}^{B}y+{C}_{2}^{B}z=-{D}_{2}^{B}\end{array}\right.$$
(7)

where:

\(\:\left[\begin{array}{c}{A}_{1}^{B}\\\:{B}_{1}^{B}\\\:{C}_{1}^{B}\end{array}\right]\triangleq\:{\overset{\rightharpoonup}{n}}_{1}^{B}\), the unit vector of normal line of the middle perpendicular plane 1;

\(\:\left[\begin{array}{c}{A}_{2}^{B}\\\:{B}_{2}^{B}\\\:{C}_{2}^{B}\end{array}\right]\triangleq\:{\overset{\rightharpoonup}{n}}_{2}^{B}\), the unit vector of normal line of the middle perpendicular plane 2;

From Eqs. (1) & (2), the elements of the unit vector are computed from the coordinates of the three-antenna position, as given by the following formula.

$$\:{\overset{\rightharpoonup}{n}}_{1}^{B}=\left[\begin{array}{c}\frac{{x}_{90}-{x}_{0}}{\sqrt{{({x}_{90}-{x}_{0})}^{2}+{({y}_{90}-{y}_{0})}^{2}+{({z}_{90}-{z}_{0})}^{2}}}\\\:\frac{{y}_{90}-{y}_{0}}{\sqrt{{({x}_{90}-{x}_{0})}^{2}+{({y}_{90}-{y}_{0})}^{2}+{({z}_{90}-{z}_{0})}^{2}}}\\\:\frac{{z}_{90}-{z}_{0}}{\sqrt{{({x}_{90}-{x}_{0})}^{2}+{({y}_{90}-{y}_{0})}^{2}+{({z}_{90}-{z}_{0})}^{2}}}\end{array}\right]\triangleq\:\left[\begin{array}{c}{A}_{1}^{B}\\\:{B}_{1}^{B}\\\:{C}_{1}^{B}\end{array}\right]$$
(8)
$$\:{\overset{\rightharpoonup}{n}}_{2}^{B}=\left[\begin{array}{c}\frac{{x}_{180}-{x}_{90}}{\sqrt{{({x}_{180}-{x}_{90})}^{2}+{({y}_{180}-{y}_{90})}^{2}+{({z}_{180}-{z}_{90})}^{2}}}\\\:\frac{{y}_{180}-{y}_{90}}{\sqrt{{({x}_{180}-{x}_{90})}^{2}+{({y}_{180}-{y}_{90})}^{2}+{({z}_{180}-{z}_{90})}^{2}}}\\\:\frac{{z}_{180}-{z}_{90}}{\sqrt{{({x}_{180}-{x}_{90})}^{2}+{({y}_{180}-{y}_{90})}^{2}+{({z}_{180}-{z}_{90})}^{2}}}\end{array}\right]\triangleq\:\left[\begin{array}{c}{A}_{2}^{B}\\\:{B}_{2}^{B}\\\:{C}_{2}^{B}\end{array}\right]$$
(9)

Methodology for horizontal axis determination

Methodology

By tilting the radar antenna around the horizontal axis to different positions and collecting GNSS observation data, the spatial equation for the horizontal axis can be solved. To maximize the angular separation and optimize GNSS positioning performance, the two GNSS antennas collect data at 4 different tilting positions of the radar antenna. First, the radar antenna is tilted at pitch of 10°,100° respectively, the primary GNSS antenna depicted as black diamond in Fig. 7 collects GNSS data. A middle perpendicular plane (as yellow plane in Fig. 7) is formed using the positioning results of the GNSS antenna position before and after radar antenna tilted. Similarly, when radar antenna is tilted at pitch of 80°,170° respectively, by using the auxiliary GNSS antenna positioning results, another middle perpendicular plane (as blue plane in Fig. 7). The intersection line of these two middle perpendicular planes defines the horizontal axis (indicated by the red dashed line).

Fig. 7
figure 7

Schematic illustration of horizontal axis determination.

Full size image

Mathematical model and algorithm for horizontal axis determination

High-precision GNSS positioning can provide accurate spatial coordinates for both the primary and auxiliary GNSS antennas when tilting the radar antenna, denoted as:

$$\:\text{P}\text{r}\text{i}\text{m}\text{a}\text{r}\text{y}\:\text{a}\text{n}\text{t}\text{e}\text{n}\text{n}\text{a}:\left({x}_{100},{y}_{100},{z}_{100}\right),\left({x}_{10},{y}_{10},{z}_{10}\right)$$
$$\:\text{A}\text{u}\text{x}\text{i}\text{l}\text{i}\text{a}\text{r}\text{y}\:\text{a}\text{n}\text{t}\text{e}\text{n}\text{n}\text{a}:\left({x}_{170},{y}_{170},{z}_{170}\right),\left({x}_{80},{y}_{80},{z}_{80}\right)$$

Using superscripts, A and B to denote the primary and auxiliary GNSS antennas, and subscripts 3 and 4 for the two middle perpendicular planes determined by the primary and auxiliary antennas, the coordinates of the midpoints of line segments between the two positioning points for each GNSS antenna are calculated as follows:

$$\:{x}_{o}^{A}=\frac{{x}_{10}+{x}_{100}}{2}$$
$$\:{y}_{o}^{A}=\frac{{y}_{10}+{y}_{100}}{2}$$
$$\:{z}_{o}^{A}=\frac{{z}_{10}+{z}_{100}}{2}$$
$$\:{x}_{o}^{B}=\frac{{x}_{80}+{x}_{170}}{2}$$
$$\:{y}_{o}^{B}=\frac{{y}_{80}+{y}_{170}}{2}$$
$$\:{z}_{o}^{B}=\frac{{z}_{80}+{z}_{170}}{2}$$

Next, the unit vector between the two points is calculated based on the coordinates of the two points as follows:

The unit vector of the line segment between the two positioning points of the primary antenna is:

$$\:{\overset{\rightharpoonup}{n}}^{A}=\left[\begin{array}{c}\frac{{x}_{100}-{x}_{10}}{{R}^{A}}\\\:\frac{{y}_{100}-{y}_{10}}{{R}^{A}}\\\:\frac{{z}_{100}-{z}_{10}}{{R}^{A}}\end{array}\right]\triangleq\:\left[\begin{array}{c}{A}_{3}^{A}\\\:{B}_{3}^{A}\\\:{C}_{3}^{A}\end{array}\right]$$
(10)

where:

$$\:{R}^{A}=\sqrt{{({x}_{100}-{x}_{10})}^{2}+{({y}_{100}-{y}_{10})}^{2}+{({z}_{100}-{z}_{10})}^{2}}$$

Similarly, the unit vector of the line segment between the two positioning points of the auxiliary antenna is:

$$\:{\overset{\rightharpoonup}{n}}^{B}=\left[\begin{array}{c}\frac{{x}_{170}-{x}_{80}}{{R}^{B}}\\\:\frac{{y}_{170}-{y}_{80}}{{R}^{B}}\\\:\frac{{z}_{170}-{z}_{80}}{{R}^{B}}\end{array}\right]\triangleq\:\left[\begin{array}{c}{A}_{4}^{B}\\\:{B}_{4}^{B}\\\:{C}_{4}^{B}\end{array}\right]$$
(11)

where:

$$\:{R}^{B}=\sqrt{{({x}_{170}-{x}_{80})}^{2}+{({y}_{170}-{y}_{80})}^{2}+{({z}_{170}-{z}_{80})}^{2}}$$

According to the point-normal form equation, the equation of the middle perpendicular plane 3 from the primary antenna can be derived:

$$\:{A}_{3}^{A}x+{B}_{3}^{A}y+{C}_{3}^{A}z=-{D}_{3}^{A}$$
(12)

where:

$$\:-{D}_{3}^{A}\triangleq\:{A}_{3}^{A}{x}_{\text{o}}^{A}+{B}_{3}^{A}{y}_{\text{o}}^{A}+{C}_{3}^{A}{z}_{\text{o}}^{A}$$

Similarly, the equation of the middle perpendicular plane 4 from the auxiliary antenna can be obtained as:

$$\:{A}_{4}^{B}x+{B}_{4}^{B}y+{C}_{4}^{B}z=-{D}_{4}^{B}$$
(13)

where:

$$\:-{D}_{4}^{B}\triangleq\:{A}_{4}^{B}{x}_{\text{o}}^{B}+{B}_{4}^{B}{y}_{\text{o}}^{B}+{C}_{4}^{B}{z}_{\text{o}}^{B}$$

The intersection line of the two middle perpendicular planes Eqs. (12) and (13) is the horizontal axis of the radar equipment, and its linear equation can be obtained by combing two plane equations as follows:

$$\:\left\{\begin{array}{c}{A}_{3}^{A}x+{B}_{3}^{A}y+{C}_{3}^{A}z=-{D}_{3}^{A}\\\:{A}_{4}^{B}x+{B}_{4}^{B}y+{C}_{4}^{B}z=-{D}_{4}^{B}\end{array}\right.$$
(14)

Determination of radar rotation center coordinates

After obtaining the linear equations of the vertical and horizontal axes, the rotation center of the radar equipment can be obtained by spatial intersecting point of two lines.

The radar center coordinates can be determined by combing and solving Eqs. (6), (7), and (14) simultaneously. Due to the existence of redundant observations, we use the least squares principle to estimate the coordinates of the radar rotation center. And the observation equation is written in matrix form26.

$$\:Z=HX$$
(15)

That is:

$$\:\left[\begin{array}{c}\begin{array}{c}-{D}_{1}^{A}\\\:-{D}_{2}^{A}\\\:-{D}_{1}^{B}\end{array}\\\:\begin{array}{c}-{D}_{2}^{B}\\\:-{D}_{3}^{A}\\\:-{D}_{4}^{B}\end{array}\end{array}\right]=\left[\begin{array}{ccc}\begin{array}{c}{A}_{1}^{A}\\\:{A}_{2}^{A}\\\:{A}_{1}^{B}\end{array}&\:\begin{array}{c}{B}_{1}^{A}\\\:{B}_{2}^{A}\\\:{B}_{1}^{B}\end{array}&\:\begin{array}{c}{C}_{1}^{A}\\\:{C}_{2}^{A}\\\:{C}_{1}^{B}\end{array}\\\:\begin{array}{c}{A}_{2}^{B}\\\:{A}_{3}^{A}\\\:{A}_{4}^{B}\end{array}&\:\begin{array}{c}{B}_{2}^{B}\\\:{B}_{3}^{A}\\\:{B}_{4}^{B}\end{array}&\:\begin{array}{c}{C}_{2}^{B}\\\:{C}_{3}^{A}\\\:{C}_{4}^{B}\end{array}\end{array}\right]\left[\begin{array}{c}x\\\:y\\\:z\end{array}\right]$$
(16)

where:

$$\:H=\left[\begin{array}{ccc}\begin{array}{c}{A}_{1}^{A}\\\:{A}_{2}^{A}\\\:{A}_{1}^{B}\end{array}&\:\begin{array}{c}{B}_{1}^{A}\\\:{B}_{2}^{A}\\\:{B}_{1}^{B}\end{array}&\:\begin{array}{c}{C}_{1}^{A}\\\:{C}_{2}^{A}\\\:{C}_{1}^{B}\end{array}\\\:\begin{array}{c}{A}_{2}^{B}\\\:{A}_{3}^{A}\\\:{A}_{4}^{B}\end{array}&\:\begin{array}{c}{B}_{2}^{B}\\\:{B}_{3}^{A}\\\:{B}_{4}^{B}\end{array}&\:\begin{array}{c}{C}_{2}^{B}\\\:{C}_{3}^{A}\\\:{C}_{4}^{B}\end{array}\end{array}\right]$$
$$\:Z=\left[\begin{array}{c}\begin{array}{c}-{D}_{1}^{A}\\\:-{D}_{2}^{A}\\\:-{D}_{1}^{B}\end{array}\\\:\begin{array}{c}-{D}_{2}^{B}\\\:-{D}_{3}^{A}\\\:-{D}_{4}^{B}\end{array}\end{array}\right]$$

\(\:X=\left[\begin{array}{c}x\\\:y\\\:z\end{array}\right]\) as the coordinate of radar rotation center.

Least squares solution is as bellow:

$$\:X={\left({H}^{{\rm\:T}}H\right)}^{-1}{H}^{{\rm\:T}}Z$$
(17)

From Eq. (17), we can obtain \(\:X={(x,y,z)}^{T}\)and its standard deviation \(\:{\sigma\:}_{X}\).

It is worth noting that the standard deviation \(\:{\sigma\:}_{X}\) depends not only on the GNSS positioning accuracy, but also on the geometric intersection of the radar equipment’s vertical and horizontal axes. The standard deviation \(\:{\sigma\:}_{X}\) includes not only GNSS positioning errors, but also model errors.

After obtaining the coordinates of the rotation center, the system error separation and accuracy evaluation of the radar angle and range measurements can be then carried out, detailed method to be provided in a separate article.

Test and validation

The research team conducted two experimental validations to compare the performance and efficiency of the new method with the traditional TST approach. Both GPS and BDS carrier phase measurements were collected for 2 h at each azimuth/pitch position. The self-developed receiver was made of BDS-3 new signal supported multi-GNSS, dual frequency receiver module, with positioning performance:

  • Static:

    $$\:\text{H}\text{o}\text{r}\text{i}\text{z}\text{o}\text{n}\text{t}\text{a}\text{l}\:\text{a}\text{c}\text{c}\text{u}\text{r}\text{a}\text{c}\text{y}\pm\:\left(2.5\hspace{0.17em}+\hspace{0.17em}0.5\:\times\:{10}^{-6}\:\times\:\:\text{D}\right)\text{m}\text{m}$$
    $$\:\text{V}\text{e}\text{r}\text{t}\text{i}\text{c}\text{a}\text{l}\:\text{a}\text{c}\text{c}\text{u}\text{r}\text{a}\text{c}\text{y}\pm\:\left(5\hspace{0.17em}+\hspace{0.17em}0.5\times\:{10}^{-6}\:\times\:\:\text{D}\right)\text{m}\text{m}$$

  • Kinematic:

    $$\:\text{H}\text{o}\text{r}\text{i}\text{z}\text{o}\text{n}\text{t}\text{a}\text{l}\:\text{a}\text{c}\text{c}\text{u}\text{r}\text{a}\text{c}\text{y}\pm\:\left(8\hspace{0.17em}+\hspace{0.17em}0.5\:\times\:\:{10}^{-6}\:\times\:\:\text{D}\right)\text{m}\text{m}$$
    $$\:\text{V}\text{e}\text{r}\text{t}\text{i}\text{c}\text{a}\text{l}\:\text{a}\text{c}\text{c}\text{u}\text{r}\text{a}\text{c}\text{y}\pm\:\left(15\hspace{0.17em}+\hspace{0.17em}0.5\:\times\:\:{10}^{-6}\:\times\:\:\text{D}\right)\text{m}\text{m}$$

Simulating radar experiment

The first validation uses a special designed radar simulated device. To improve research efficiency, we designed and produced radar simulated device, as depicted in Fig. 8, which served as a foundation for the experimental investigation of the theoretical analysis, observation methods, and data processing algorithms presented in this paper. A metal thin ruler was installed inside the device as illustrated in Fig. 8, the intersection point of this ruler and horizontal axis directly presents the rotation center which can be observed directly by total station.

Fig. 8
figure 8

Photo of radar simulated device (photo by research team).

Full size image

From September 11 to 14, 2023, we conducted four tests on the radar simulated device to determine the radar rotation center coordinates. At the same time, a comparison was made between the traditional method based on TST and the new method based on high-precision GNSS positioning.

Test results of the TST method

During our test process, two total stations with prisms and three control points (known coordinates given in Table 1) nearby the radar simulated device were engaged in.

Table 1 Control points with known coordinates.
Full size table

Utilizing TST forward-intersection method from three known control points to derive the coordinate of the rotation center point, totally 11 measurement rounds had been implemented. The resulted coordinates as shown in Table 2.

Table 2 Results of the rotation center coordinates.
Full size table

Table 2 shows that the positioning accuracy of traditional method is slightly larger than 10millimeters.

Test results of the new method

During our test process, the GNSS receivers with antennas were deployed according to Fig. 4. Following the operation flowchart of Fig. 5, completing all data collection (over four time periods), carrying out data processing with the model and algorithm provided in Chap. 3, the coordinates of the rotation center point of radar simulated device were obtained. Lets’ take the first time as an example, give, step by step, the rotation center positioning results, as shown in Tables 3, 4 and 5, and 6. The results will be given in details in the following.

The GNSS antenna position coordinates were first solved and shown in Table 3.

Table 3 Positioning Results of GNSS Primary and Auxiliary antennas.
Full size table

Using these ten antenna coordinates, the equation of each middle perpendicular plane was solved, shown in Table 4.

Table 4 Solution for the equation of middle perpendicular planes.
Full size table

According to the least squares principle, the six plane equations in the above table were combined and solved to obtain the coordinates of the rotation center point with its accuracy are shown in Table 5.

Table 5 Coordinate of the rotation center point and its standard deviation (m).
Full size table

Similarly, we can process GNSS data of other three time periods, and obtain the three sets of rotation center coordinates, as the list 1–4 shown in Table 6. Then simply averaging the results of all four time periods, leads to the final solution of the rotation center’s position coordinates with its standard deviation shown also in Table 6.

Table 6 Final solution of the rotation center’s position coordinates with its standard deviation.
Full size table

Table 6 shows that the positioning accuracy of the new method is slightly better than 3millimeters.

Accuracy comparison of two methods

A comparison of the results from both methods revealed an average difference of less than 5 millimeters, with the maximum discrepancy being 4.4 millimeters, as detailed in Table 7.

Table 7 Comparison of the results between two methods.
Full size table

Table 7 shows that the horizontal positioning accuracy of the new method is much better than TST with 79% improvement.

Real-scene test and validation

On November 13–14, 2023, the research team and a third-party professional surveying team conducted a real-scene test of radar rotation center determination based on an operational radar equipment at a TT&C monitoring site of China.

Test results of the TST method

During test period, the third-party professional surveying team consisting of 8 surveyors, implemented radar rotation center measurement by TST method employing two total stations with prisms and five control points. According to the procedure described in Chap. 2, three steps were implemented as below:

  • Step 1: Use angle bisector method to intersect the quasi-center point position and mark it.

  • Step 2: Utilizing TST forward-intersection method from known control points to derive the coordinate of the marked quasi-center point.

  • Step3: Transform quasi-center’ coordinate to radar rotation center by simply downward half-height of the pitch-box along the vertical axis.

Test results of the new method

During test period, 2 persons of our research team carried out the test and validation of the new method and provided radar rotation center coordinates by using the same equipment and operation process as that of Chap. 4.1.

The radar rotation center positions determined with two methods are shown in Table 8, and their comparisons in terms of operation efficiency and accuracy.

Table 8 Results and comparisons of the two methods.
Full size table

The comparison shows that the new method requires fewer equipment, fewer participants, and shorter working hours compared to the TST method, with 60% efficiency improvement. The accuracy of the new method could reach millimeter level, with 45% accuracy improvement.

Conclusions

To determine the rotation center of Space TT&C radar equipment, this paper proposes a new technique that is an analytic geometry method in 3D space by using high precision GNSS satellite measurements. The innovation idea is that inaccessible point position determination problem is converted to a simple determining intersection of planes and lines, for which the high precision GNSS satellite measurements were here used to calculate the plane-equation, intersection lines-equation and then the intersection point position as the radar rotation center. This method is comprehensively better than traditional TST technique in terms of measurement accuracy, operation efficiency, and cost-effective, breaking through the technical automation bottleneck of TST method such as ‘manual eye-aiming, manual operation, step-by-step calculation’.

It also expands methods and the scene of the GNSS application for achieving high-precision positioning measurements in challenging environments. Experiment and validation from both simulation & real-scene radar test shows that the new method is stable and reliable in performance. It reduces the technical difficulty of space TT&C radar rotation center determination and simplifies the operation procedure. It only needs simple training for deployment and has a wide application prospect such as astronomical theodolite bias calibration, various radars bias calibration, various large scale machinery surveying in GNSS signal-challenging environments.